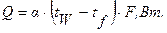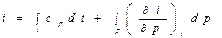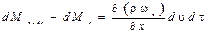1 дифференциальное уравнение конвективного теплообмена

Основные теоретические сведения. 2.1.1 Дифференциальное уравнение конвективного теплообмена

2.1.1 Дифференциальное уравнение конвективного теплообмена. Критерии подобия

Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости или газа. При этом перенос тепла осуществляется одновременно конвекцией и теплопроводностью. Конвективный теплообмен между потоком жидкости или газа и поверхностью твердого тела называется конвективной теплоотдачей или теплоотдачей.

При практических расчетах теплоотдачи используется закон Ньютона-Рихмана:

Здесь Q– тепловой поток от стенки к жидкости, Вт; F – поверхность теплообмена, м 2 ; a – коэффициент теплоотдачи, Вт/м 2 ×град; t_W – температура стенки, град; t_f – температура жидкости, град.

Различают вынужденную и естественную конвенцию. В первом случае жидкость или газ движутся за счет внешних для данного процесса сил (насос, ветер и т.д.), во втором случае – за счет разности плотностей нагретых и холодных частиц жидкости.

На процесс конвективного теплообмена существенно влияет характер движения жидкости. Из гидродинамики известно, что имеются два основных режима течения: ламинарный и турбулентный. При ламинарном режиме частицы жидкости движутся, не перемешиваясь; при турбулентном – движутся неупорядоченно, хаотически; направление и величина скорости отдельных частиц непрерывно меняются.

Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. В настоящее время точные решения уравнений имеются только для отдельных частных случаев. Поэтому большое значение приобретает экспериментальный путь исследования.

Теоретической базой экспериментальных исследований является теория подобия. С помощью теории подобия размерные физические величины объединяются в безразмерные комплексы, причем так, что число комплексов меньше числа величин, составляющих эти комплексы. Полученные безразмерные комплексы рассматриваются как новые переменные. Теория подобия устанавливает также условия, при которых результаты лабораторных исследований можно распространить на другие явления, подобные рассматриваемому.

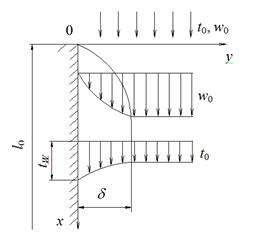
Пусть поверхность твердого тела омывается несжимаемой жидкостью, температура и скорость которой вдали от тела постоянны и равны соответственно t₀и w₀. Размеры тела ℓ₀ и другие параметры заданы. Температура поверхности тела равна t_W. Примем, что t_W> t₀, а также, что физические параметры тела постоянны. Теплота трения не учитывается. Рассматриваемый процесс является стационарным.

Расположим оси координат так, как показано на рисунке 2.1. Ось z направлена перпендикулярно плоскости чертежа.

При принятых условиях конвективный теплообмен описывается системой дифференциальных уравнений:

, (2.2)

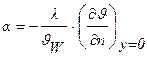
где J = t — t₀, t – температура жидкости; J_W = t_W — t₀; n – нормаль к поверхности;

(2.3),

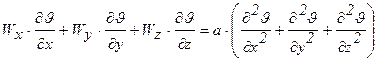
где 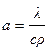— коэффициент температуропроводности жидкости,

r, с – соответственно, плотность и удельная теплоемкость жидкости;

(2.4а)

(2.4б)

(2.4в)

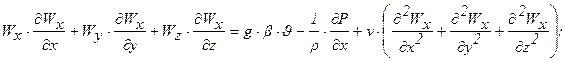
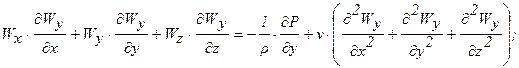
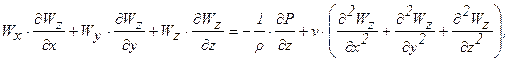
где Р – давление жидкости,

n — коэффициент кинематической вязкости жидкости;

. (2.5)

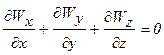
1. Вдали от тела (х

зависимые переменные – a, J, W_x, W_y, W_z и P; они однозначно определяются значениями независимых переменных, если заданы величины, входящие в условия однозначности;

постоянные величины – W₀, t₀, ℓ₀, J_c, n, a, l, b, r и др., они задаются условиями однозначности и для определенной задачи являются постоянными величинами, не зависящими от других переменных; от задачи к задаче они могут меняться.

Таким образом, искомые зависимые переменные a, J, W_x, W_y, W_z и P зависят от большого числа величин: они являются функциями переменных и постоянных величин, входящих в условия однозначности.

Величины, содержащиеся в уравнениях и условиях однозначности, можно сгруппировать в безразмерные комплексы. Число безразмерных комплексов будет меньше числа размерных величин. Для приведения уравнений и условий однозначности к безразмерному виду выбирают масштабы приведения. В качестве масштабов удобно принять постоянные величины, входящие в условия однозначности.

Дата добавления: 2015-12-26 ; просмотров: 3084 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Дифференциальное уравнение конвективного теплообмена

Для вывода дифференциального уравнения конвективного теплообмена в установившемся потоке жидкости (газа) выделяют элементарный параллелепипед с гранями dx, dy, dz (рис. 7.2) и составляют для него тепловой баланс, приняв физические параметры λ, с_р и ρ постоянными. Скорости движения жидкости в направлении осей x, y и z, соответственно – w_x, w_y и w_z. Температура жидкости t изменяется вдоль граней параллелепипеда. Теплоперенос в жидкости осуществляется путем конвекции и теплопроводности. Все подведенное к параллелепипеду тепло затрачивается только на изменение его энтальпии.

Количество тепла, которое вводится жидкостью путем конвекции по направлению оси х через грань dydz за время dτ,

.

За это же время через противоположную грань параллелепипеда путем конвекции жидкостью выводится количество тепла

,

.

Разность между количествами введенного и выведенного тепла в направлении оси х за время dτ составит:

.

Аналогично в направлении осей y и z

;

.

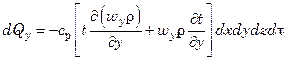
Полная разность между количествами введенного и выведенного путем конвекции тепла в объеме параллелепипеда за время dτ

.

На основании уравнения неразрывности потока (1.34)

.

Тогда конвективная составляющая теплового потока

,

где – объем параллелепипеда.

Количество тепла, которое вводится в параллелепипед жидкостью путем теплопроводности за время dτ, в соответствии с уравнением (7.21)

.

Суммарное количество тепла, подведенное конвекцией и теплопроводностью

Это тепло dQ, согласно первому началу термодинамики, равно изменению энтальпии жидкости в объеме параллелепипеда

.

.

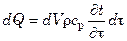
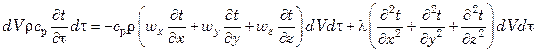
В результате простейших преобразований последнего равенства, получим

,

, (7.66)

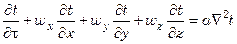
где – коэффициент температуропроводности.

Полученное уравнение (7.66) является дифференциальным уравнением конвективного теплообмена, или уравнением Фурье-Кирхгофа. Оно выражает в наиболее общем виде распределение температур в движущемся потоке жидкости (газа).

Для твердых тел w_x = w_y = w_z = 0 и уравнение (7.66) превращается в дифференциальное уравнение теплопроводности (7.23).

При установившемся процессе теплообмена , тогда уравнение конвективного теплообмена для этого случая

. (7.67)

Ввиду сложности уравнения (7.66) для практического использования его подобно преобразовывают с учетом условий однозначности, т.е. представляют в виде функции от критериев подобия. Для этого, с целью более полного описания конвективного переноса тепла, дифференциальное уравнение Фурье-Кирхгофа дополняется граничными условиями, вытекающими из закона теплообмена на границе твердого тела и окружающей его среды.

Тепловое подобие

На практике процессы теплообмена осуществляются с помощью потоков разнообразных жидкостей и газов при различных режимах их движения в аппаратах различной геометрической формы и размеров. Однако условия подобия во всех случаях одинаковы и сводятся к подобию геометрических параметров, полей скоростей и температуры, а также физических констант. При этом должно соблюдаться подобие переноса тепла, как в пограничном слое, так и в ядре потока жидкости (газа).

Подобие переноса тепла в пограничном слое можно установить из краевых условий теплообмена на границе твердое тело – жидкость (газ), воспользовавшись зависимостью (7.64):

.

Применив тот же метод подобного преобразования уравнений, что и при выводе критериев гидродинамического подобия (см. раздел 1.3.6), разделим правую часть последнего равенства на левую:

.

Заменив на характерный (определяющий) геометрический размер , получим безразмерный комплекс величин, называемый критерием Нуссельта:

. (7.68)

Критерий Нуссельта характеризует теплоперенос через пограничный слой в форме соотношения количества тепла, передаваемого конвекцией, и теплопроводностью.

Аналогом критерия Нуссельта при нестационарном теплообмене между твердым телом и жидкостью или газом является критерий Био:

, (7.69)

где – коэффициент теплопроводности твердого тела.

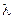
Условия подобия в ядре потока определяются из уравнения Фурье-Кирхгофа (7.66). Для одномерного движения потока жидкости его можно представить в виде

. (7.70)

Поделив члены левой части на правую часть, отбросив знаки математических операторов и заменив величины и на характерный геометрический размер и осредненную скорость соответственно, получим

;

.

Полученный комплекс обычно для удобства заменяют обратной величиной , которая выражает необходимое условие подобия неустановившихся процессов теплообмена. Этот безразмерный комплекс получил название критерия Фурье:

. (7.71)

Комплекс является мерой соотношения между теплом, переносимым конвекцией и теплопроводностью при конвективном теплообмене, и носит название критерия Пекле:

. (7.72)

Необходимым условием теплового подобия являются предшествующие ему гидродинамическое и геометрическое подобия. Гидродинамическое подобие определяется критериями гомохронности Но, Рейнольдса Re и Фруда Fr, а геометрическое – постоянством отношений основных геометрических размеров поверхности (стенки) к некоторому характерному размеру L. В качестве характерного линейного размера для трубных поверхностей, которые часто используются в качестве теплопередающих, принимают диаметр трубы L = d, иногда – длину трубы L = l, радиус кривизны изогнутой трубы L = R и т.д. В результате критериальное уравнение конвективного теплообмена выражается функцией вида

, (7.73)

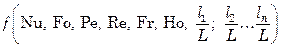
где – симплексы геометрического подобия.

Равенство критериев Нуссельта является следствием подобия геометрических и физических характеристик, а также подобия полей скоростей и температур. Поэтому Nu не является определяющим. В связи с этим обобщенную зависимость, описывающую кинетику переноса тепла в движущихся средах, представляют в виде

. (7.74)

Критерий Пекле обычно представляют в виде двух безразмерных комплексов

,

где – критерий Прандтля, характеризующий физические свойства теплоносителя (жидкости или газа).

По физическому смыслу критерий Pr определяет соотношение полей скоростей и температур в потоке. Для капельных жидкостей он зависит от температуры (с повышением температуры увеличивается), а его численные значения лежат в пределах 3 ÷ 300. Для газов критерий Прандтля не зависит ни от температуры, ни от давления, являясь постоянной величиной для газов одинаковой атомности (для одноатомных газов Pr = 0,67; для двухатомных Pr = 0,72; для трехатомных Pr = 0,8; для четырехатомных и более Pr = 1).

С введением критерия Прандтля уравнение (7.74) принимает вид:

. (7.75)

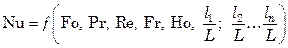
При установившихся тепловых процессах и одинаковой геометрической форме потоков из уравнения (7.75) исключаются критерии Fo и Ho, содержащие время, и геометрические симплексы, тогда

. (7.76)

При рассмотрении конкретных задач теплообмена уравнение (7.76) может быть видоизменено.

Так, при вынужденном движении, когда влияние сил тяжести на гидродинамику потока пренебрежительно мало, критерием Фруда можно пренебречь и критерий Нуссельта будет являться функцией лишь двух критериев:

. (7.77)

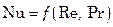
При свободном движении жидкости (в условиях естественной конвекции) из критериального уравнения исключают критерий Рейнольдса:

. (7.78)

Ввиду сложности определения скорости при естественной конвекции, входящей в критерий Фруда, последний заменяют производным критерием Архимеда, характеризующим естественную конвекцию, обусловленную разностью плотностей жидкости (газа) в различных точках потока:

,

где ρ и ρ₀ – плотности холодной и нагретой жидкости (газа).

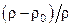
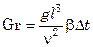
Поскольку в тепловых процессах разность плотностей в различных точках системы обусловливается разностью температур Δt нагретой и холодной жидкости, комплекс в критерии Архимеда целесообразно выразить через произведение bΔt (b – температурный коэффициент объемного расширения). Полученный новый критерий является критерием Грасгофа:

. (7.79)

Таким образом, критерий Gr представляет собой определяющий критерий теплового подобия при естественной конвекции, когда движение жидкости целиком обусловлено самим процессом теплообмена, а уравнение конвективного теплообмена для этого случая

. (7.80)

Для газов при Pr ≈ 1 уравнение (7.79) превращается в функциональную зависимость критерия Нуссельта от критерия Грасгофа.

Помимо приведенных критериев теплового подобия в литературе часто встречаются производные критерии, составленные из указанных выше:

критерий Стантона , (7.81)

который отражает соотношение количества тепла, передаваемого конвекцией, и тепла, переносимого движущимся потоком;

критерий Релея ; (7.82)

критерий Грэтца 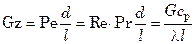, (7.83)

(G – массовый расход жидкости) характеризует конвективный теплоперенос при ламинарном режиме.

.

В соответствии с полученными критериальными уравнениями обрабатываются опытные данные по переносу тепла конвекцией и представляются в виде степенных уравнений. Например, уравнение (7.77) – в виде ; уравнение (7.79) – в виде и т.д.

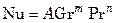
При решении практических задач по найденному из соответствующего критериального уравнения значению критерия Нуссельта определяют коэффициент теплоотдачи:

.

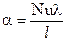
Критериальные зависимости в виде степенных уравнений, как уже указывалось, решают чисто эмпирически и применимы они лишь в тех пределах изменения аргумента, в которых подтверждены опытом. Поэтому области их надежного применения ограничены пределами, указываемыми в каждом отдельном случае. Ограничения эти, в основном, связаны с характером и режимом движения потока теплоносителя, его геометрической формой и размерами, изменением агрегатного состояния.

Дифференциальные уравнения конвективного теплообмена

следует, что плотность теплового потока в любой точке жидкости для каждого момента времени однозначно определяется, если известны поля температур, удельной энтальпии и скорости.

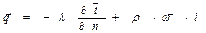
Связь между температурой и энтальпией может быть установлена следующим образом. Для реальной жидкости , и согласно понятию о полном дифференциале

Отсюда

Для многих задач в предположении о несжимаемости жидкости (ρ=const) с достаточной степенью точности можно принять , т.е. пользоваться соотношением, справедливым для термодинамически идеального газа:

и .

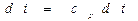
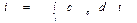
Выведем диф­ференциальное уравнение, описывающее тем­пературное поле в движущейся жидкости.

При выводе будем полагать, что:

— её физические параметры постоянны,

— энергия деформации мала по срав­нению с изменением внутренней энергии.

Выделим в потоке жидкости неподвиж­ный относительно координатной системы эле­ментарный параллелепипед с реб­рами dx, dy и dz.

Через грани параллелепипе­да теплота переносится теплопроводностью и конвекцией; в общем случае в рассматривае­мом объеме может выделяться теплота внутренними источниками.

Вывод уравнения энергии, соответствующего принятым здесь усло­виям, был получен ранее:

,

Проекции плотности теплового потока на координатные оси Ох, Оу и Оz равны

, и

Подставляя значения q_x,q_y и q_z в уравнение Фурье, можно получить

Для несжимаемых жидкостей (ρ=const) из закона сохранения массы следует:

или, если ,

Последнее уравнение является уравнением энергии, описывающим распределение температур внутри движущейся жидкости.

Если , уравнение энергии переходит в уравнение теплопроводности.

Как следует из уравнения энергии, темпера­турное поле в движущейся жидкости зависит от составляющих скорости .

Чтобы сде­лать систему уравнений замкнутой, необходимо добавить уравнения, которые бы описывали из­менение скорости во времени и пространстве. Такими уравнениями являются дифференциаль­ные уравнения движения.

Уравнение движения вдоль оси Ох

.

Описание движения жидкости усложняется, если скорость изменя­ется по трем направлениям.

для оси Оz

В общем случае составляющие скорости изменяются во времени и в пространстве. Член, стоящий в левой части уравнений, представляет собой полную производную от скорости по времени.

На основании понятия о полной (субстанциальной) производной для оси Ох имеем

Аналогичные уравнения можно записать и для осей Оу, Оz.

Используя векторную форму записи:

Уравнение движения получено без учета зависимости физи­ческих параметров жидкости от температуры. В частности, не учтена зависимость плотности от температуры.

В то же время свободное дви­жение жидкости определяется разностью плотностей холодных и нагре­тых частиц жидкости.

Приближенный учет переменности плотности возможен с введением температурного коэффициента объемного расши­рения β.

Т.к. в уравнение движения, помимо входит еще неизвестная величина р, то система уравнений не является замкнутой. Необходимо добавить еще одно уравнение – уравнение сплошности (неразрывности).

Выде­лим в потоке движущейся жидкости непо­движный элементарный параллелепипед со сторонами dx, dy и dz и подсчитаем массу жидкости, протекающей через него в на­правлении осей Ох, Оу и Oz за время dτ.

В направлении оси Ох в параллелепи­пед втекает масса жидкости

Величина представляет собой ко­личество массы, протекающей в единицу времени через единицу поперечного сече­ния. Из противоположной грани вытекает масса

Ограничиваясь первыми двумя членами разложения в ряд, полу­чаем, что масса dM_x+dx, вытекающая из элементарного параллелепида в направлении оси Ох:

Излишек массы жидкости, вытекающий из элементарного объема в направлении оси Ох:

Аналогичным образом можно получить уравнения для направлений по осям Оу и Оz.

Полный избыток мас­сы жидкости, вытекающей из элементарного объема в направлении всех трех осей обуславливается измене­нием плотности жидкости в объеме dυ и равен изменению массы дан­ного объема во времени .

Произведя сокращение на dυ и dτ и перенеся все члены в левую часть равенства, окончательно получим дифференциальное уравнение сплошности для сжимаемых жидкостей

Для несжимаемых жидкостей, полагая ρ=const, получаем

Уравнение сплошности является уравнением сохранения массы.