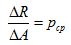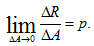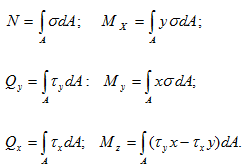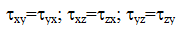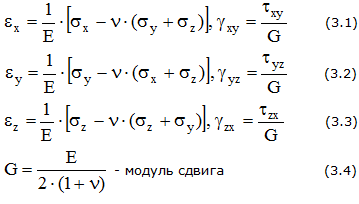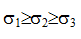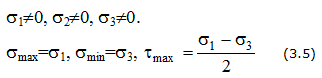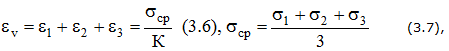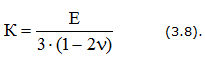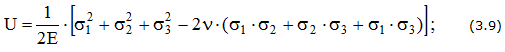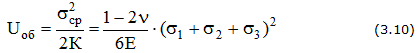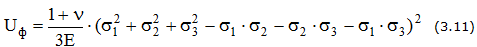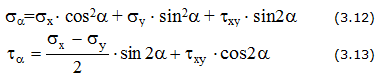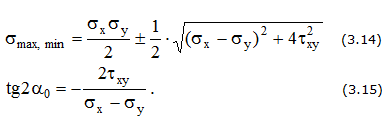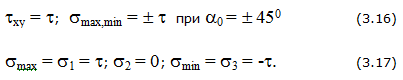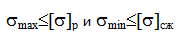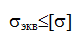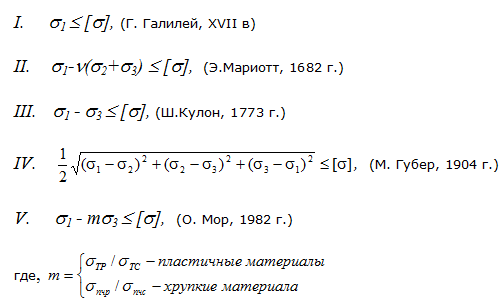1 характеристическое уравнение напряженного состояния

1 характеристическое уравнение напряженного состояния

Рассмотрим важный для приложений случай плоского напряженного состояния, реализуемого, например, в плоскости Oyz. Тензор напряжений в этом случае имеет вид

Геометрическая иллюстрация представлена на рис.1. При этом площадки х=const являются главными с соответствующими нулевыми главными напряжениями. Инварианты тензора напряжений равны , а характеристическое уравнение принимает вид

Корни этого уравнения равны

Нумерация корней произведена для случая

Рис.1. Исходное плоское напряженное состояние.

Рис.2. Позиция главных напряжений

Произвольная площадка характеризуется углом на рис. 1, при этом вектор п имеет компоненты: , , n_х=0. Нормальное и касательное напряжения на наклонной площадке выражаются через угол следующим образом:

Так как на главных площадках касательное напряжение отсутствует, то, приравнивая нулю выражение (3), получим уравнение для определения угла между нормалью п и осью Оу

Наименьший положительный корень уравнения (4) обозначим через . Так как tg(х)—периодическая функция с периодом , то имеем два взаимно ортогональных направления, составляющие углы и с осью Оу. Эти направления соответствуют взаимно перпендикулярным главным площадкам (рис. 2).

Если продифференцировать соотношение (2) по и приравнять производную нулю, то придем к уравнению (4), что доказывает экстремальность главных напряжений.

Для нахождения ориентации площадок с экстремальными касательными напряжениями приравняем нулю производную от выражения

,

Сравнивая соотношения (4) и (5), находим, что

Это равенство возможно, если углы и отличаются на угол . Следовательно, направления площадок с экстремальными касательными напряжениями отличаются от направлений главных площадок на угол (рис. 3).

Рис.3. Экстремальность касательных напряжений

Величины экстремальных касательных напряжений получим после подстановки (5) в соотношение (3) с использованием формул

.

После некоторых преобразований получим

Сравнивая это выражение с полученными ранее значениями главных напряжений (2.21), выразим экстремальные касательные напряжения через главные напряжения

Аналогичная подстановка в (2) приводит к выражению для нормальных напряжений на площадках с

Полученные соотношения позволяют проводить направленно-ориентированный расчет конструкций на прочность в случае плоского напряженного состояния.

Рассмотрим вначале случай плоской деформации (рис. 4). Пусть плоский элемент MNPQ перемещается в пределах плоскости и деформируется (изменяет форму и размеры). Координаты точек элемента до и после деформации отмечены на рисунке.

Рис.4. Плоская деформация.

По определению относительная линейная деформация в точке М в направлении оси Ох равна

Из рис. 4 следует

Учитывая, что MN=dx, получим

В случае малых деформаций, когда , , можно пренебречь квадратичными слагаемыми. С учетом приближенного соотношения

iSopromat.ru

Рассмотрим понятие о напряженном состоянии в точке и гипотезы прочности. Связь между напряжениями и внутренними силами. Объемное, плоское и линейное напряженное состояния.

Понятие о напряжениях в точке

На основании допущения о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению.

Выделим в произвольной точке малую площадку ΔA, а равнодействующую внутренних сил на этой площадке обозначим ΔR. Отношение

представляет собой среднее напряжение на данной площадке.

Если площадку ΔA уменьшить, то в пределе получим полное напряжение в точке

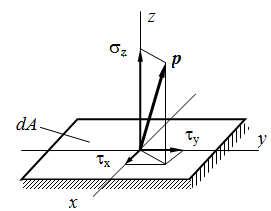
Полное напряжение р может быть разложено на три составляющие: по нормали к плоскости сечения и по двум осям в плоскости сечения. Проекция вектора полного напряжения р на нормаль обозначается через σ и называется нормальным напряжением.

Составляющие в плоскости сечения называются касательными напряжениями и обозначаются τ. В зависимости от расположения и наименования осей обозначения σ и τ снабжаются системой индексов.

Связь между напряжениями и внутренними силами

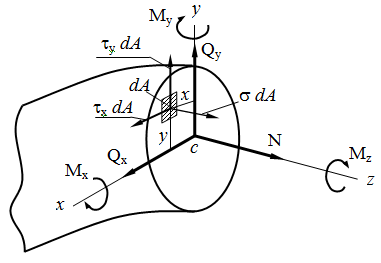
Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dA и приложим к ней элементарные силы σ dA, τ_x dA, τ_y dA.

Знак «А» у интеграла показывает, что интегрирование проводится по всей площади поперечного сечения. Приведённые формулы позволяют определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению.

Обратную задачу с помощью только одних этих уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например N, могут соответствовать различные законы распределения нормальных напряжений по сечению.

Одной из основных задач сопротивления материалов является задача об определении напряжений через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформации бруса.

Объемное напряженное состояние

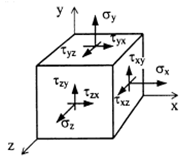
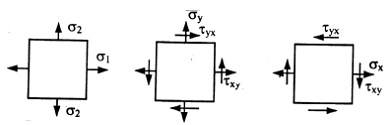
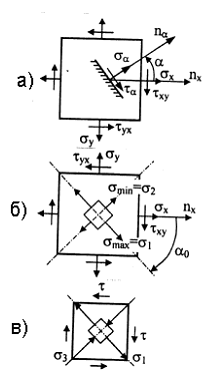
Совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку, составляет напряженное состояние в рассматриваемой точке. На площадках общего положения действуют нормальные и касательные напряжения (рис. 3.1).

Значения касательных напряжений на взаимно перпендикулярных площадках подчиняются закону парности касательных напряжений:

Площадки, на которых отсутствуют касательные напряжения, называются главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями (рис. 3.2).

Обозначение главных напряжений:

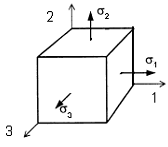
Напряженное состояние называется объемным или трехосным, если

Относительное изменение объема:

где К – модуль объемной упругости,

Удельная потенциальная энергия упругой деформации:

Плоское напряженное состояние

Напряженное состояние называется плоским или двухосным, если одно из главных напряжений равно нулю (рис. 3.3).

Напряжения на наклонной площадке (рис. 3.4,а)

Величина и направление главных напряжений (рис. 3.4,б)

Линейное напряженное состояние

Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю.

Проверка прочности при линейном напряженном состоянии проводится по условию прочности:

В сложном напряженном состоянии проверку прочности проводят по гипотезам прочности по эквивалентному напряжению:

Величина σ_экв определяется, исходя из принятого критерия эквивалентности, лежащего в основе одной из гипотез разрушения или гипотез прочности, при котором сложное напряженное состояние заменяется эквивалентным ему растяжением или сжатием.

Гипотезы прочности

Существует 5 гипотез прочности:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Напряженное и деформированное состояние

Напряженное и деформированное состояние

Различают три вида напряженного состояния:

1) линейное напряженное состояние — растяжение (сжатие) в одном направлении;

2) плоское напряженное состояние — растяжение (сжатие) по двум направлениям;

3) объемное напряженное состояние — растяжение (сжатие) по трем взаимно перпендикулярным направлениям.

Рассматривают бесконечно малый параллелепипед (кубик). На его гранях могут быть нормальные s и касательные t напряжения. При изменении положения «кубика» напряжения меняются. Можно найти такое положение, при котором нет касательных напряжений см. рис.

Площадки, по которым не действуют касательные напряжения, называются главными площадками, а нормальные напряжения на этих площадках — главными напряжениями.

Главные напряжения обозначают: s1, s2, s3 и s1> s2> s3

Плоское напряженное состояние

Разрежем элементарный параллелепипед (рис. а) наклонным сечением. Изображаем только одну плоскость. Рассматриваем элементарную треугольную призму (рис. б). Положение наклонной площадки определяется углом a. Если поворот от оси x против час. стр. (см. рис. б), то a>0.

Нормальные напряжения имеют индекс, соответствующий оси их направления. Касательные напряжения, обычно, имеют два индекса: первый соответствует направлению нормали к площадке, второй — направлению самого напряжения (к сожалению, встречаются и другие обозначения, и другой выбор осей координат, что приводит к изменению знаков в некоторых формулах).

Нормальное напряжение положительно, если оно растягивающее, касательное напряжение положительно, если оно стремится повернуть рассматриваемую часть элемента относительно внутренней точки по час. стр (для касательного напряжения в некоторых учебниках и вузах принято обратное).

Напряжения на наклонной площадке:

или

Закон парности касательных напряжений: если по площадке действует касательное напряжение, то по перпендикулярной к ней площадке будет действовать касательное напряжение, равное по величине и противоположное по знаку. (txz= — tzx)

В теории напряженного состояния различают две основные задачи.

Прямая задача. По известным главным напряжениям: s1= smax, s2= smin требуется определить для площадки, наклоненной под заданным углом (a) к главным площадкам, нормальные и касательные напряжения:

или .

Для перпендикулярной площадки:

.

Откуда видно, что sa+sb=s1+s2 — сумма нормальных напряжений по двум взаимно перпендикулярным площадкам инварианта (независима) по отношению к наклону этих площадок.

Как и в линейном напряженном состоянии максимальные касательные напряжения имеют место при a=±45о, т. е. по площадкам, наклоненным к главным площадкам под углом 45о .

Обратная задача. По известным нормальным и касательным напряжениям, действующим в двух взаимно перпендикулярных площадках, найти главные (max и min) напряжения и положение главных площадок.

(касательные напряжения по главным площадкам равны 0).

Угол a0, определяющий положение главных площадок: или .

Если одно из главных напряжений окажется отрицательным, то их надо обозначать s1, s3, если оба отрицательны, то s2, s3.

Объемное напряженное состояние

Напряжения в любой площадке при известных главных напряжениях s1, s2, s3:

;

,

где a1, a2, a3 — углы между нормалью к рассматриваемой площадке и направлениями главных напряжений.

Наибольшее касательное напряжение: .

Оно действует по площадке параллельной главному напряжению s2 и наклоненной под углом 45о к главным напряжениям s1 и s3.

Круг Мора для объемного напряженного состояния.

Точки, являющиеся вершинами кругов соответствуют диагональным площадкам, наклоненным под 45о к главным напряжениям:

, (иногда называют главными касательными напряжениями).

Плоское напряженное состояние — частный случай объемного и тоже может быть представлено тремя кругами Мора, при этом одно из главных напряжений должно быть равно 0. Для касательных напряжений также, как и при плоском напряженном состоянии, действует закон парности: составляющие касательных напряжений по взаимно перпендикулярным площадкам, перпендикулярные к линии пересечения этих площадок, равны по величине и обратны по направлению.

Напряжения по октаэдрической площадке.

Октаэдрическая площадка (АВС) – площадка, равнонаклоненная ко всем главным направлениям.

;

Октаэдрическое нормальное напряжение равно среднему из трех главных напряжений.

или , Октаэдрическое касательное напряжение пропорционально геометрической сумме главных касательных напряжений. Интенсивность напряжений:

.

sx+sy+sz=s1+s2+s3 — сумма нормальных напряжений, действующих по любым трем взаимно перпендикулярным площадкам есть постоянная величина, равная сумме главных напряжений (первый инвариант).

Деформации при объемном напряженном состоянии.

Обобщенный закон Гука (закон Гука при объемном напряжении):

e1,e2,e3 — относительные удлинения в главных направлениях (главные удлинения). Если какие-либо из напряжений si будут сжимающими, то их необходимо подставлять в формулы со знаком минус.

Относительная объемная деформация:

Изменение объема не зависит от соотношения между главными напряжениями, а зависит от суммы главных напряжений. Т. е. элементарный кубик получит такое же изменение объема, если к его граням будут приложены одинаковые средние напряжения: , тогда , где К= — модуль объемной деформации. При деформации тела, материал которого имеет коэффициент Пуассона m= 0,5 (например, резина) объем тела не меняется.

Потенциальная энергия деформации

При простом растяжении (сжатии) потенциальная энергия U=.

Удельная потенциальная энергия — количество потенциальной энергии, накапливаемое в единице объема: u = ; . В общем случае объемного напряженного состояния, когда действуют три главных напряжения:

или

Полная энергия деформации, накапливаемая в единице объема, может рассматриваться как состоящая из двух частей: 1) энергии uo, накапливаемой за счет изменения объема (т. е. одинакового изменения всех размеров кубика без изменения кубической формы) и 2) энергии uф, связанной с изменением формы кубика (т. е. энергии, расходуемой на превращение кубика в параллелепипед). u = uо + uф.

;

— тензор напряжений (матрица третьего порядка).

При переходе к главным напряжениям тензор напряжений получает вид:

. При повороте системы координат коэффициенты тензора меняются, сам тензор остается постоянным.

Три инварианта напряженного состояния:

Аналогичные зависимости возникают при рассмотрении деформированного состояния в точке. Сопоставление зависимостей напряженного и деформированного плоского состояния (аналогия):

ea — относительная деформация, ga — угол сдвига.

Та же аналогия сохраняется и для объемного состояния. Поэтому имеем инварианты деформированного состояния:

J2= exey +eyez + ezex — g2xy — g2yz — g2zx;

— тензор деформаций.

ex, ey, ez, gxy, gyz, gzx — компоненты деформированного состояния.

Для осей, совпадающих с направлениями главных деформаций e1, e2, e3, тензор деформаций принимает вид: .

Теории прочности

В общем случае опасное напряженное состояние элемента конструкции зависит от соотношения между тремя главными напряжениями (s1,s2,s3). Т. е., строго говоря, для каждого соотношения нужно экспериментально определять величину предельного напряжения, что нереально. Поэтому были приняты такие методы расчета прочности, которые позволяли бы оценить степень опасности любого напряженного состояния по напряжению растяжения – сжатия. Они называются теориями прочности (теории предельных напряженных состояний).

1-ая теория прочности (теория наибольших нормальных напряжений): причиной наступления предельного напряженного состояния являются наибольшие нормальные напряжения. smax= s1£ [s]. Главный недостаток: не учитываются два других главных напряжения. Подтверждается опытом только при растяжении весьма хрупких материалов (стекло, гипс). В настоящее время практически не применяется.

2-ая теория прочности (теория наибольших относительных деформаций): причиной наступления предельного напряженного состояния являются наибольшие удлинения. emax= e1£ [e]. Учитывая, что e1=, m — коэффициент Пуассона, получаем условие прочности sэквII= s1 — m(s2 + s3)£ [s]. sэкв — эквивалентное (расчетное) напряжение. В настоящее время теория используется редко, только для хрупких материалов (бетон, камень).

3-я теория прочности (теория наибольших касательных напряжений): причиной наступления предельного напряженного состояния являются наибольшие касательные напряжения tmax £ [t], tmax=, условие прочности: sэквIII= s1 — s3£ [s]. Основной недостаток – не учитывает влияние s2.

При плоском напряженном состоянии: sэквIII= £ [s]. При sy=0 получаем Широко используется для пластичных материалов.

4-я теория прочности (энергетическая теория): причиной наступления предельного напряженного состояния являются величина удельной потенциальной энергии изменения формы. uф£[uф]. .

Учитывает, все три главных напряжения. При плоском напряженном состоянии: . При sy=0,

Широко используется для пластичных материалов.

Теория прочности Мора Получена на основе кругов напряжений Мора. . Используется при расчетах хрупких материалов, у которых допускаемые напряжения на растяжение [sp] и сжатие [sс] не одинаковы (чугун).

Для пластичных материалов [sp]=[sс] теория Мора превращается в 3-ю теорию.

Круг Мора (круг напряжений). Координаты точек круга соответствуют нормальным и касательным напряжениям на различных площадках. Откладываем от оси s из центра С луч под углом 2a (a>0, то против час. стр.), находим точку D,

координаты которой: sa, ta. Можно графически решать как прямую, так и обратную задачи.

Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения , где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т. е. это частный случай плоского напряженного состояния, при котором главные напряжения: s1= — s3 = t; s2= 0. Главные площадки составляют с площадками чистого сдвига угол 45о.

При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. d — абсолютный сдвиг,

g » — относительный сдвиг или угол сдвига.

Закон Гука при сдвиге: g = t/G или t = G×g.

G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е — модуль упругости, m— коэффициент Пуассона).

Потенциальная энергия при сдвиге: .

Удельная потенциальная энергия деформации при сдвиге: ,

где V=а×F — объем элемента. Учитывая закон Гука, .

Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.

Круг Мора при чистом сдвиге.

Кручение

Такой вид деформации, при котором в поперечных сечениях возникает только одни крутящие моменты — Мк. Знак крутящего момента Мк удобно определять по направлению внешнего момента. Если при взгляде со стороны сечения внешний момент направлен против час. стр., то Мк>0 (встречается и обратное правило). При кручении происходит поворот одного сечения относительно другого на угол закручивания — j. При кручении круглого бруса (вала) возникает напряженное состояние чистого сдвига (нормальные напряжения отсутствуют), возникают только касательные напряжения. Принимается, что сечения плоские до закручивания остаются плоскими и после закручивания — закон плоских сечений. Касательные напряжения в точках сечения изменяются пропорционально расстоянию точек от оси. Из закона Гука при сдвиге: t=gG, G — модуль сдвига, , — полярный момент сопротивления круглого сечения. Касательные напряжения в центре равны нулю, чем дальше от центра, тем они больше. Угол закручивания , GJp — жесткость сечения при кручении. — относительный угол закручивания. Потенциальная энергия при кручении: . Условие прочности: , [t] =, для пластичного материала за tпред принимается предел текучести при сдвиге tт, для хрупкого материала – tв – предел прочности, [n] – коэффициент запаса прочности. Условие жесткости при кручении: qmax£[q] – допустимый угол закручивания.

Кручение бруса прямоугольного сечения

При этом нарушается закон плоских сечений, сечения некруглой формы при кручении искривляются – депланация поперечного сечения.

Эпюры касательных напряжений прямоугольного сечения.

; , Jk и Wk — условно называют моментом инерции и моментом сопротивления при кручении. Wk= ahb2,

Jk= bhb3, Максимальные касательные напряжения tmax будут посредине длинной стороны, напряжения по середине короткой стороны: t= g×tmax, коэффициенты: a, b,g приводятся в справочниках в зависимости от отношения h/b (например, при h/b=2, a=0,246; b=0,229; g=0,795.

Изгиб

Плоский (прямой) изгиб — когда изгибающий момент действует в плоскости, проходящей через одну из главных центральных осей инерции сечения, т. е. все силы лежат в плоскости симметрии балки. Основные гипотезы (допущения): гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения – сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N>0, если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются, снизу растягиваются. .

Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения: , r — радиус кривизны нейтрального слоя, y — расстояние от некоторого волокна до нейтрального слоя. Закон Гука при изгибе: , откуда (формула Навье): , Jx — момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента, EJx — жесткость при изгибе, — кривизна нейтрального слоя.

Максимальные напряжения при изгибе возникают в точках, наиболее удаленных от нейтрального слоя: , Jx/ymax=Wx—момент сопротивления сечения при изгибе, .

Если сечение не имеет горизонтальной оси симметрии, то эпюра нормальных напряжений s не будет симметричной. Нейтральная ось сечения проходит через центр тяжести сечения. Формулы для определения нормального напряжения для чистого изгиба приближенно годятся и когда Q¹0. Это случай поперечного изгиба. При поперечном изгибе, кроме изгибающего момента М, действует поперечная сила Q и в сечении возникают не только нормальные s, но и касательные t напряжения. Касательные напряжения определяются формулой Журавского: , где Sx(y) — статический момент относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии «y» от нейтральной оси; Jx — момент инерции всего поперечного сечения относительно нейтральной оси, b(y) — ширина сечения в слое, на котором определяются касательные напряжения.

Для прямоугольного сечения: , F=b×h, для круглого сечения:, F=p×R2, для сечения любой формы ,

k— коэфф., зависящий от формы сечения (прямоугольник: k= 1,5; круг — k= 1,33).

Mmax и Qmax определяются из эпюр изгибающих моментов и поперечных сил. Для этого балка разрезается на две части и рассматривается одна из них.

Действие отброшенной части заменяется внутренними силовыми факторами М и Q, которые определяются из уравнений равновесия. В некоторых вузах момент М>0 откладывается вниз, т. е. эпюра моментов строится на растянутых волокнах. При Q= 0 имеем экстремум эпюры моментов. Дифференциальные зависимости между М,Q и q:

q — интенсивность распределенной нагрузки [кН/м]

Главные напряжения при поперечном изгибе:

.

Расчет на прочность при изгибе: два условия прочности, относящиеся к различным точкам балки: а) по нормальным напряжениям , (точки наиболее удаленные от С); б) по касательным напряжениям , (точки на нейтр. оси). Из а) определяют размеры балки: , которые проверяют по б). В сечениях балок могут быть точки, где одновременно большие нормальные и большие касательные напряжения. Для этих точек находятся эквивалентные напряжения, которые не должны превышать допустимых. Условия прочности проверяются по различным теориям прочности

I-я: ; II-я: (при коэфф. Пуассона m=0,3); — применяются редко.

III-я:, IV-я:,

теория Мора: , (используется для чугуна, у которого допускаемое напряжение на растяжение [sр]¹[sс] – на сжатие).

Определение перемещений в балках при изгибе

Имеем закон Гука при изгибе: , где r(х) — радиус кривизны изогнутой оси балки в сечении х, М(х) — изгибающий момент в том же сечении, EJ — жесткость балки. Из высшей математики известно: — дифференциальное уравнение изогнутой оси балки. — тангенс угла между осью х и касательной к изогнутой оси. Эта величина очень мала (прогибы балки малы) Þ ее квадратом пренебрегают и угол поворота сечения приравнивают тангенсу. Приближенное дифференциальное ур-ние изогнутой оси балки: . Если ось y направлена вверх, то знак (+). В некоторых вузах ось y направляется вниз Þ(—). Интегрируя дифф. уравнение, получаем: — ур-ние углов поворота, интегрируем второй раз: — получаем ур-ние прогибов. Постоянные интегрирования С и D находятся из граничных условий, которые зависят от способов закрепления балки.

Метод начальных параметров. Начало координат выбирают в крайней левой точке. При включении в уравнение момента М, который приложен на расстоянии «а» от начала координат, его умножают на множитель (х — а)0, который равен 1. Любую распределенную нагрузку продлевают до конца балки, а для ее компенсации прикладывают нагрузку обратного направления.

EJ= M(x) = RA×x – – M(x – a)0 + – P(x – a – b); интегрируем:

EJ = EJq0 + RA× – – M(x – a) + – P;

EJy =EJy0 + EJq0x + RA× – – M + – P.

Начальные параметры — то, что мы имеем в начале координат, т. е. для рис.: М0=0, Q0=RA, прогиб y0=0, угол поворота q0¹0. q0 находим из подстановки во второе уравнение условия закрепления правой опоры: x=a+b+c; y(x)=0.

Дифференциальные зависимости при изгибе:

; ; ; .

Определение перемещений способом фиктивной нагрузки. Сопоставляя уравнения:

и имеем аналогию, Þ определение прогибов можно свести к определению моментов от некоторой фиктивной (условной) нагрузки в фиктивной балке: . Момент от фиктивной нагрузки Мф после деления на EJ равен прогибу «y» в заданной балке от заданной нагрузки. Учитывая, что и , получаем, что угол поворота в заданной балке численно равен фиктивной поперечной силе в фиктивной балке. , . При этом должна быть полная аналогия в граничных условиях двух балок. Каждой заданной балке соответствует своя фиктивная балка.

Закрепление фиктивных балок выбирается из того условия, чтобы на концах балки и на опорах имелось полное соответствие между «y» и «q» в заданной балке и Мф и Qф в фиктивной балке. Если эпюры моментов как в действительной, так и в фиктивной балках строить со стороны растянутого волокна (т. е. положительный момент откладывать вниз), то линии прогибов в заданной балке совпадает с эпюрой моментов в фиктивной балке.

Статически неопределимые балки.

Статически неопределимыми называются системы, реакции в которых не могут быть определены из уравнений равновесия твердого тела. В таких системах больше связей, чем это необходимо для равновесия. Степень статической неопределимости балки (не имеющей промежуточных шарниров – неразрезные балки) равна избыточному (лишнему) числу внешних связей (более трех).

Раскрытие статической неопределимости с помощью дифф-ного урав-ния изогнутой оси балки. Записываем дифф-ное урав-ние куда входит в качестве неизвестной реакция RB и дважды его интегрируем: EJ= RВ×x – ; EJ = RВ× – + С;

EJy = RВ× – + С×х + D. Используем условия закрепления балки: х=0, y=0, =0; x=L, y=0. Подставляем их в два последних уравнения, находи постоянные интегрирования С и D и неизвестную реакцию RB. Далее из урав-ний статики: HA=0; RA – q×L + RB=0; RB×L – + MA=0; находятся RA и MA.

Уравнение совместности перемещений. Статически определимая балка, которая получается из статически неопределимой при удалении «лишнего» закрепления, называется основной системой. За «лишнюю» неизвестную можно взять любую из реакций. Приложив к основной системе заданные нагрузки добавляем условие, которое обеспечивает совпадение заданной балки и основной – уравнение совместности перемещений. Для рис.: yB=0, т. е. прогиб в точке В = 0. Решение этого уравнения возможно разными способами.

Способ сравнения перемещений. Определяется прогиб точки В (рис.) в основной системе под действием заданной нагрузки (q): yВq=. Далее рассматривается основная система под действием «лишней» неизвестной RB, и находится прогиб от действия RB: . Подставляем в уравнение совместности перемещений: yB= yВq += 0, т. е. += 0, откуда RB=, далее остальные реакции находятся из уравнений статики.

Теорема о трех моментах. Используется при расчете неразрезных балок — балок на многих опорах, одна из которых неподвижна, остальные подвижны. Для перехода от статически неопределимой балки к статически определимой основной системе над –лишними опорами вставляются шарниры. Лишними неизвестные: моменты Mn, приложенные к концам пролетов над лишними опорами.

Строятся эпюры моментов для каждого пролета балки от заданной нагрузки, рассматривая каждый пролет, как простую балку на двух опорах. Для каждой промежуточной опоры «n» составляется уравнение трех моментов:

wn, wn+1–площади эпюр, an – расстояние от центра тяжести левой эпюры до левой опоры, bn+1 – расстояние от центра тяжести правой эпюры до правой опоры. Число уравнений моментов равно числу промежуточных опор. Совместное их решение позволяет найти неизвестные опорные моменты. Зная опорные моменты, рассматриваются отдельные пролеты и из уравнений статики находятся неизвестные опорные реакции. Если пролета всего два, то левый и правый моменты известны, т. к. это либо заданные моменты, либо они равны нулю. В результате получаем одно уравнение с одним неизвестным М1.

Общие методы определения перемещений

Работа постоянных сил: А=Р×DР, Р – обобщенная сила – любая нагрузка (сосредоточенная сила, сосредоточенный момент, распределенная нагрузка), DР – обобщенное перемещение (прогиб, угол поворота). Обозначение Dmn означает перемещение по направлению обобщенной силы «m» , которое вызвано действием силы обобщенной «n». Полное перемещение, вызванное несколькими силовыми факторами: DР=DРP+DРQ+DРM. Перемещения вызванные единичной силой или единичным моментом: d – удельное перемещение. Если единичная сила Р=1 вызвала перемещение dР, то полное перемещение вызванное силой Р, будет: DР=Р×dР. Если силовые факторы, действующие на систему, обозначить Х1,Х2,Х3 и т. д., то перемещение по направлению каждого из них:

где Х1d11=+D11; Х2d12=+D12; Хidmi=+Dmi. Размерность удельных перемещений: , Дж — джоули размерность работы 1Дж = 1Нм.

Работа внешних сил, дейст-щих на упругую систему: .

– действительная работа при статическом действии обобщенной силы на упругую систему равна половине произведения окончательного значения силы на окончательное значение соответствующего перемещения. Работа внутренних сил (сил упругости) в случае плоского изгиба: ,

k – коэффициент, учитывающий неравномерность распределения касательных напряжений по площади поперечного сечения, зависит от формы сечения.

На основании закона сохранения энергии: потенциальная энергия U=A.

Теорема о взаимности работ (теорема Бетли). Два состояния упругой ситемы:

D11– перемещение по направл. силы Р1 от действия силы Р1;

D12– перемещение по направл. силы Р1 от действия силы Р2;

D21– перемещение по направл. силы Р2 от действия силы Р1;

D22– перемещение по направл. силы Р2 от действия силы Р2.

А12=Р1×D12 – работа силы Р1 первого состояния на перемещении по ее направлению, вызванном силой Р2 второго состояния. Аналогично: А21=Р2×D21 – работа силы Р2 второго состояния на перемещении по ее направлению, вызванном силой Р1 первого состояния. А12=А21. Такой же результат получается при любом числе сил и моментов. Теорема о взаимности работ: Р1×D12=Р2×D21.

Работа сил первого состояния на перемещениях по их направлениям, вызванных силами второго состояния, равна работе сил второго состояния на перемещениях по их направлениям, вызванных силами первого состояния.

Теорема о взаимности перемещений (теорема Максвелла) Если Р1=1 и Р2=1, то Р1d12=Р2d21, т. е. d12=d21, в общем случае dmn=dnm.

Для двух единичных состояний упругой системы перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй единичной силы, вызванному первой силой.

Универсальный метод определения перемещений (линейных и углов поворота) – метод Мора. К системе прикладывают единичную обобщенную силу в точке, для которой ищется обобщенное перемещение. Если определяется прогиб, то единичная сила представляет собой безразмерную сосредоточенную силу, если определяется угол поворота, то – безразмерный единичный момент. В случае пространственной системы действуют шесть компонентов внутренних усилий. Обобщенное перемещение определяется формулой (формула или интеграл Мора):

Черта над М, Q и N указывает на то, что эти внутренние усилия вызваны действием единичной силы. Для вычисления входящих в формулу интегралов надо перемножить эпюры соответствующих усилий. Порядок определения перемещения: 1) для заданной (действительной или грузовой) системы находят выражения Mn, Nn и Qn; 2) по направлению искомого перемещения прикладывают соответствующую ему единичную силу (силу или момент); 3) определяют усилия от действия единичной силы; 4) найденные выражения подставляют в интеграл Мора и интегрируют по заданным участкам. Если полученное Dmn>0, то перемещение совпадает с выбранным направлением единичной силы, если 0, если переход от старой системы координат к новой происходит против час. стр. Jy1 + Jx1= Jy + Jx

Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т. е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей: , если a0>0 Þ оси поворачиваются против час. стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:

Jmax + Jmin= Jx + Jy. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям:

Jx1=Jmaxcos2a + Jminsin2a; Jy1=Jmaxcos2a + Jminsin2a; Jx1y1=(Jmax — Jmin)sin2a;

Конечной целью вычисления геометрических характеристик сечения является определение главных центральных моментов инерции и положения главных центральных осей инерции. Радиус инерции — ; Jx=F×ix2, Jy=F×iy2.

Если Jx и Jy главные моменты инерции, то ix и iy — главные радиусы инерции. Эллипс, построенный на главных радиусах инерции как на полуосях, называется эллипсом инерции. При помощи эллипса инерции можно графически найти радиус инерции ix1 для любой оси х1. Для этого надо провести касательную к эллипсу, параллельную оси х1, и измерить расстояние от этой оси до касательной. Зная радиус инерции, можно найти момент инерции сечения относительно оси х1: . Для сечений, имеющих более двух осей симметрии (например: круг, квадрат, кольцо и др.) осевые моменты инерции относительно всех центральных осей равны между собой, Jxy=0, эллипс инерции обращается в круг инерции.

Осевой момент сопротивления — отношение момента инерции относительно оси к расстоянию от нее до наиболее удаленной точки сечения. [см3, м3]

Особенно важны моменты сопротивления относительно главных центральных осей:

прямоугольник: ; круг: Wx=Wy= ,

трубчатое сечение (кольцо): Wx=Wy= , где a= dН/dB.

Полярный момент сопротивления — отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения: .

Для круга Wр= .

Растяжение и сжатие

N = s×F

s — нормальное напряжение [Па], 1Па (паскаль) = 1 Н/м2,

106Па = 1 МПа (мегапаскаль) = 1 Н/мм2

N — продольная (нормальная) сила [Н] (ньютон); F — площадь сечения [м2]

e — относительная деформация [безразмерная величина];

DL — продольная деформация [м] (абсолютное удлинение), L — длина стержня [м].

— закон Гука — s = Е×e

Е — модуль упругости при растяжении (модуль упругости 1-го рода или модуль Юнга) [МПа]. Для стали Е= 2×105МПа = 2×106 кг/см2 (в «старой» системе единиц).

(чем больше Е, тем менее растяжимый материал)

; — закон Гука

EF — жесткость стержня при растяжении (сжатии).

При растяжении стержня он «утоньшается», его ширина — а уменьшается на поперечную деформацию — Dа.

— относительная поперечная деформация.

— коэффициент Пуассона [безразмерная величина];

m лежит в пределах от 0 (пробка) до 0,5 (каучук); для стали m »0,25¸0,3.

Если продольная сила и поперечное сечение не постоянны, то удлинение стержня:

Работа при растяжении: , потенциальная энергия:

Учет собственного веса стержня

Продольная сила N(z) = P + g×F×L;

Р — сила, действующая на стержень, g — удельный вес, F — площадь сечения.

Максимальное напряжение: . Деформация:

Условие прочности при растяжении (сжатии) smax£ [s],

[s] — допускаемое напряжение на растяжение (сжатие).

У чугуна [sраст]¹[sсж], у стали и др. пластичных материалов [sраст]=[sсж].

Основные механические характеристики материалов

sп— предел пропорциональности, sт— предел текучести, sВ— предел прочности или временное сопротивление, sк— напряжение в момент разрыва.

Хрупкие материалы, напр., чугун разрушаются при незначительных удлинениях и не имеют площадки текучести, лучше сопротивляются сжатию, чем растяжению.

Допускаемое напряжение , s0— опасное напряжение, n — коэф. запаса прочности. Для пластичных материалов s0 = sт и n = 1,5, хрупких s0 = sВ, n = 3.

Линейное напряженное состояние

напряжения по наклонной площадке:

полное :

нормальное: , касательное:

Fa — площадь наклонной площадки.

Нормальные напряжения sa положительны, если они растягивающие; касательные напряжения ta положительны, если они стремятся повернуть рассматриваемый элемент (нижняя часть) по часовой стрелке ( на рис. все положительно). Наибольшие нормальные напряжения возникают по площадкам перпендикулярным к оси стержня (a=0, cosa=1, maxsa= s)

На перпендикулярных площадках: b = — (90 — a)

; , т. е. tb = — ta.

Наибольшие касательные напряжения действуют по площадкам, составляющим угол 45о к оси стержня (a=45о, sin2a=1, maxta= s/2)

Напряженное и деформированное состояние…………………1

Объемное напряженное состояние……………………………4

Напряжения по октаэдрической площадке…………………..5

Деформации при объемном напряженном состоянии.

Обобщенный закон Гука ………………………………………6

Потенциальная энергия деформации…………………………7

Теории прочности………………………………………………9

Теория прочности Мора ………………………………………10

Закон Гука при сдвиге…………………………………………12

Кручение………………………………………………………..13

Кручение бруса прямоугольного сечения…………………….14

Изгиб……………………………………………………………15

Расчет на прочность при изгибе………………………………18

Определение перемещений в балках при изгибе……………19

Дифференциальные зависимости при изгибе……………….20

Уравнение совместности перемещений……………………..22

Способ сравнения перемещений……………………………..22

Теорема о трех моментах……………………………………..22

Общие методы определения перемещений………………….24

Теорема о взаимности работ (теорема Бетли)……………….25

Теорема о взаимности перемещений (теорема Максвелла).. 26

Вычисление интеграла Мора способом Верещагина……….27

Статически неопределимые системы………………………..29

Расчет плоских кривых брусьев (стержней)………………. 31

Устойчивость сжатых стержней. Продольный изгиб………33

Геометрические характеристики плоских сечений…………36

Моменты инерции сечения…………………………………..37

Центробежный момент инерции сечения …………………..37

Моменты инерции сечений простой формы………………..38

Моменты инерции относительно параллельных осей……..39

Зависимость между моментами инерции при повороте

Растяжение и сжатие…………………………………………43

Основные механические характеристики материалов…….45