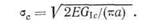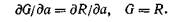1 критерии роста трещины уравнение пэриса

Критерий роста трещины

Увеличение длины трещины происходит тогда, когда величина G равна энергии, необходимой для роста трещины. В истинно хрупких материалах, например таких, как стекло, энергией, оказывающей влияние на рост трещины, является поверхностная энергия, необходимая для образования новых свободных поверхностей, т. е.

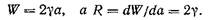Уравнение (5.1) можно разрешить с помощью уравнений (5.6) и (5.15), откуда получаем:

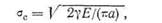что и является критерием Гриффитса [1, 2].

Ирвин [6] и Орован [7] заметили, что энергия, необходимая для роста трещины в металле, намного превосходит поверхностную энергию, необходимую для обра-

зования новых свободных поверхностей. В металлах перед трещиной образуются пластические деформации, и во время распространения трещины энергия расходуется на образование зоны пластичности при вершине распространяющейся трещины. Если пластическая энергия R для одинаковых приращений размеров различных трещин одинакова, то величина R p=s dWIda остается постоянной. Из эксперимента следует, что это приблизительно верно для трещин,

распространяющихся при плоской деформации: образцы с трещина— ми различных размеров, как оказывается, разрушаются при одних и тех же значениях G. Это критическое значение G обозначают как G_k;= (1 -v*)Kl/E.

Следовательно, в случае плоской деформации R р= dWIda — G\_c, откуда следует, что

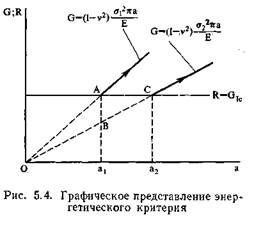
Критерий разрушения можно изобразить графически так, как показано на рис. 5.4. Сопротивление росту трещины R не зависит

от размера трещины; поэтому эта величина представлена на рисунке прямой горизонтальной линией R τ= G\_c. Интенсивность выделения энергии

(5.18)

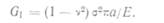
При заданном напряжении a_i скорость выделения энергии пропорциональна размеру трещины а. Для этого случая величина G представлена на рисунке линией О А. Если трещина имеет размер о_ь то скорость выделения энергии при напряжении σ₂ представлена точ-

кой В. При увеличении напряжения от σ₂ до a_t величина G увеличивается от точки В до точки А. В точке А может произойти увеличение размера трещины, так как выполняется условие G >= R. В более длинной трещине размера а₂ эта ситуация возникает уже при напряжении σ₂ (точка С).

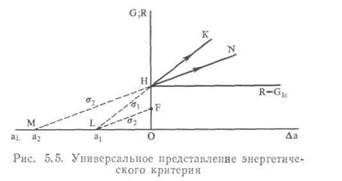
Более универсальное представление критерия разрушения приведено на рис. 5.5. Вправо отложена величина приращения длины трещины Δα, а влево —начальный размер трещины а_г Как и прежде, величина G представлена прямыми линиями, например при напряжении σ₂ величина G задана линией LF. Из всех точек линии LF реальную ситуацию описывает только точка F, поскольку с самого начала размер трещины равен а₁. При возрастании нагрузки на трещину от нуля до σ₂ соответствующая ей величина G возрастает от 0 до F. Дальнейшее увеличение напряжения до величины а _<приводит к увеличению G до точки Н. После этого происходит разрушение. Расширение трещины при напряжении а₁ приводит к изменению G вдоль линии FIK, и, следовательно, G остается большим, чем R.

Если нагрузка на трещину размера а₂ возрастает от нуля до σ₂, то соответствующее ей значение G увеличивается от 0 до Я (обратите внимание на то, что линии LF и МН параллельны). В точке Η происходит увеличение длины трещины: если напряжение остается равным σ₂, то скорость выделения энергии изменяется вдоль линии ΗΝ и G остается большим, чем R.

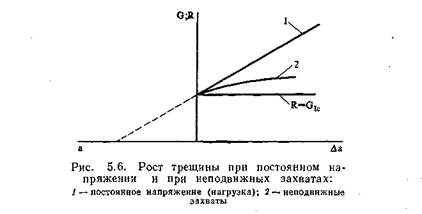
В § 5.1 было показано, что в обоих случаях роста трещины при постоянном напряжении и при фиксированных захватах величина G

имеет одно и то же значение. Однако это имеет место только ι начале процесса увеличения длины трещины. В процессе роста трещины это условие не выполняется. Если распространение трещины происходит при постоянном напряжении, то G меняется вдоль прямых линий, как показано на рис. 5.5. Если рост трещины происходит при неподвижных захватах, то напряжение уменьшается. Поскольку то отсюда следует, что величина G увеличивается не пропорциональ-

но а, а медленнее (рис. 5.6). При определенной геометрии образца, если рост трещины происходит при неподвижных захватах, G может даже уменьшиться. Обсуждению этой задачи, а также вытекающих отсюда следствий посвящена гл. VI.

§ 5.3. Сопротивление росту трещины (R-кривая)

До сих пор величина R рассматривалась как не зависящая от длины трещины. Это приблизительно верно для трещин, находящихся в плоском деформированном состоянии. В случае плоского напряженного состояния сопротивление росту трещины, как было показано в экспериментах, изменяется.

Рассмотрим трещину в листе, достаточно тонком для того, чтобы в нем возникло плоское напряженное состояние (см. гл. VII и VIII). Когда образец нагружен до напряжения σ_;, начинается процесс распространения трещины. Однако процесс роста трещины пока стабилен и разрушение еще не наступает. Если напряжение остается равным σ., то трещина распространяется только на небольшое расстояние и останавливается. Для поддержания процесса роста трещины необходимо дальнейшее увеличение напряжения: несмотря на то что трещина стала длиннее, она может выдержать большие напряжения. Процесс одновременного увеличения размера трещины и напряжения может быть продолжен, пока при напряжении а_с не будет достигнут критический размер трещины а_с, при котором возникает неустойчивость, предшествующая разрушению. Этот процесс проиллюстрирован на рис. 5.7.

В начале процесса роста трещины должен выполняться энергетический критерий. При стабильном росте трещины скорость выделения энергии в точности равна сопротивлению росту трещины (если она меньше, то трещина прекращает расти, если больше, то возни-

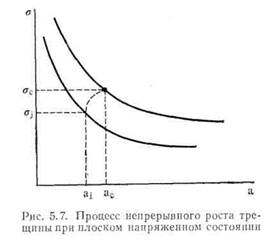кает нестабильность, предшествующая разрушению). Скорость выделения энергии G ¢= π σ 2 αίΕ, и во время роста трещины увеличивается как σ, так и а. Это означает, что G увеличивается не пропорционально а, а быстрее. Так как G ¢= R, то отсюда следует заключить, что R увеличивается так, как показано графически на рис. 5.8. Пусть трещина размера а. нагружена до напряжения α ι. Если бы трещина росла, то количество выделяемой при этом энергии было бы задано точкой А. Однако эта вели-

чина слишком мала для того, чтобы трещина росла. Напряжение может быть далее увеличено до σ.; скорость выделения энергии при этом будет задана точкой В

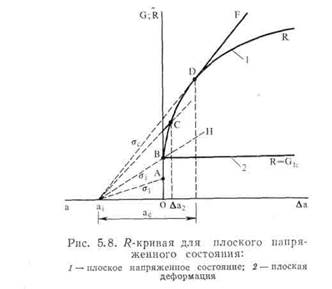
Пусть это значение достаточно для роста трещины. Если бы трещина распространялась при постоянном напряжении, то величина G увеличивалась бы по линии ВН. Эта линия лежит ниже ^-кривой, и поэтому при постоянном напряжении трещина расти не может.

Дальнейшее увеличение напряжения до величины σ₂ приводит к увеличению размера трещины на Аа₂. Величины G и R изменяются вдоль ^-кривой от β к С. Наконец, при напряжении о_с длина трещины становится равной а_с, а величины G и R доходят до точки D. Рост трещины при постоянном напряжении а_с сопровождается увеличением G по линии DF. Эта линия лежит выше ^-кривой. Поскольку G остается большим, чем R, происходит окончательное разрушение в точке D, в которой

Уравнение (5.19), очевидно, представляет собой энергетический критерий для разрушения при плоском напряженном состоянии. Количественная оценка этого критерия разрушения возможна, если будет получено аналитическое выражение для ^-кривой. Попытки вывода этого выражения были сделаны в работах [8—11]. Оценка критерия разрушения проведена в гл. VIII.

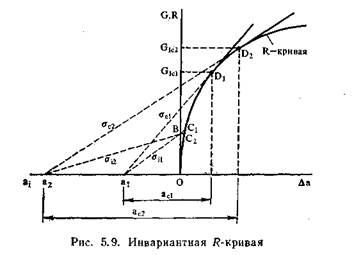
Крафт и др. [12] сделали предположение, что ^-кривая инвариантна: она имеет одинаковый вид безотносительно к начальному размеру трещины. Это означает, что условие разрушения для трещин произвольных размеров следует из графического построения, которое выполнено на рис. 5.9, где касательные для различных длин трещин проведены к единственной /^-кривой.

7?-кривая представляет собой энергию, необходимую для роста трещины. В вязком материале эта энергия слагается из работы, необходимой для образования новой зоны пластичности при вершине развивающейся трещины, и работы, необходимой для образования,

роста и слияния микропустот. Наиболее вероятно, что последняя мала по сравнению с энергией, содержащейся в зоне пластичности. Поэтому ^-кривая должна начинаться в нулевой точке, как показано на рис. 5.9: при нулевых напряжениях размер зоны пластичности равен нулю. Это также означает, что при любом напряжении, отличном от нуля, выполняется энергетический критерий (не считая работы образования пустот). Однако трещина не растет, поскольку напряжения и пластические деформации все еще недостаточны. Энергетический критерий является критерием необходимым, но недостаточным.

Материал при вершине трещины не будет готов к расцеплению, пока напряжения и деформации не станут достаточно велики, чтобы стало возможно образование и слияние пустот. К моменту, когда возникает такая ситуация, образуется довольно большая зона пластичности. Трещина может расти только в том случае, если в процессе ее роста выделяется достаточно энергии, чтобы совершить работу по образованию зоны пластичности при новой вершине трещины. Трещина не может расти, если не удовлетворено это энергетическое условие; она должна расти, если это условие удовлетворено.

Легко видеть, что все линии роста трещин пересекаются в точке В (рис. 5.9). Эта точка является общей для трещин с размерами а_л и а₂, поэтому

(5.20)

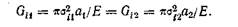
Стабильный рост трещины начинается при определенном значении G, а именно при G_;, заданном уравнением (5.20). При G, равном G., рост трещины происходит от точки В до точки Ci или С₂, где G ?= R. Это первое отдельное расширение трещины называется хлопком, потому что представляет собой внезапное метастабильное расширение трещины, которое часто сопровождается звучным щелчком. После хлопка происходит непрерывный стабильный медленный рост трещины, пока в точке D_± или D₂ не последует разрушение.

Для двух рассматриваемых трещин значения G равны соответственно G_lcl и G_ic2. Это означает, что критическая скорость выделения энергии для плоского напряженного состояния G_ic не является постоянной величиной и, поскольку К 2 и = EG_ic, отсюда величина Ki_c также непостоянна (индекс 1 используется здесь для обозначения плоского напряженного состояния в трещине типа I, чтобы отличать Ки и G_lc от значений К\с и G\_c при плоской деформации). В отличие от случая плоской деформации, когда G\_c и К\с в определенных пределах являются константами материала, величины G_ic и Ki_c зависят от размера трещины и для больших трещин имеют большие значения.

В § 5.1 было отмечено, что с помощью соотношения К 2 1 = EG_i к величине G можно применить коррекцию на конечность размеров. Используя при этом коррекцию Ирвина [3] (см. гл. III), получим

(5.21)

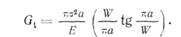
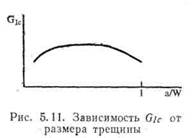
Уравнение (5.21) означает, что линии G —не прямые, а имеют положительную кривизну, как показано на рис. 5.10. Для маленькой трещины коррекцией на конечность размеров можно пренебречь и считать линию G приблизительно прямой. По мере удлинения трещин увеличивается и кривизна. В результате значение G_lc сначала уве-

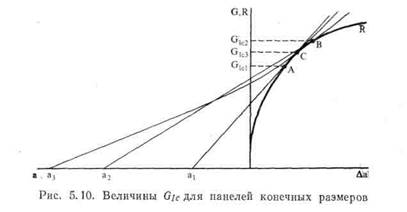личивается от G_ici до G_ic2, а затем вновь уменьшается до G_lcS, как показано на рис. 5.11.

Были предложены различные формы ^-кривых (см. [13]), некоторые из которых приведены на рис. 5.12. Горизонтальная часть

этих кривых используется для объяснения явления хлопка. Однако скорее всего ^-кривые начинаются в нулевой точке. Рис. 5.9 показывает, что хлопок может произойти и в том случае, если /^-кривая начинается в нулевой точке. Форма R-кривой зависит от толщины пластины. Для толстых пластин, находящихся в плоском деформированном состоянии, они представляют собой пря-

мую горизонтальную линию. Для тонких пластин, находящихся в плоском напряженном состоянии, /^-кривая имеет ступеньку и возрастающий участок. Переходной зоне пластин промежуточной толщины соответствует ^-кривая, форма которой является чем-то средним между этими двумя крайними случаями.

Теория ^-кривых до конца еще не разработана. В гл. VIII приведена дальнейшая информация о ^-кривых и процессе разрушения при плоском напряженном состоянии. Здесь же представлены R-кривые, полученные экспериментально.

Дата добавления: 2015-06-22 ; просмотров: 2271 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

1 критерии роста трещины уравнение пэриса

Электронный научный журнал «ТРУДЫ ВИАМ»

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ УНИТАРНОЕ ПРЕДПРИЯТИЕ
«ВСЕРОССИЙСКИЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ АВИАЦИОННЫХ МАТЕРИАЛОВ»
НАЦИОНАЛЬНОГО ИССЛЕДОВАТЕЛЬСКОГО ЦЕНТРА «КУРЧАТОВСКИЙ ИНСТИТУТ»
ГОСУДАРСТВЕННЫЙ НАУЧНЫЙ ЦЕНТР РОССИЙСКОЙ ФЕДЕРАЦИИ

Авторизация

Статьи

Скорость роста трещины усталости (СРТУ) является необходимой составляющей в комплексе механических свойств, который характеризует надежность материалов для авиационной техники.

Проведено исследование СРТУ жаропрочных титановых сплавов ВТ8-1, ВТ41, ВИТ1 при комнатной и рабочих температурах, двух коэффициентах асимметрии цикла (0,1 и 0,5). Установлено, что параметры уравнения Пэриса (C и n) для исследованных жаропрочных титановых сплавов не являются независимыми и аппроксимируются общей прямой линией в координатах «lgC–lgn».

Работа выполнена в рамках реализации комплексного научного направления 2.2. «Квалификация и исследования материалов» («Стратегические направления развития материалов и технологий их переработки на период до 2030 года»)

Введение

Жаропрочные титановые сплавы широко применяются в качестве материалов для ответственных деталей газотурбинных энергетических установок [1–3]. В процессе эксплуатации материал деталей подвергается сложному температурно-силовому нагружению. Основным критерием сравнения и применимости материалов в конструкции являются их механические характеристики прочности. Для жаропрочных титановых сплавов большое значение имеют характеристики прочности, определяемые при высоких температурах [4–6].

Для материалов ротора компрессора большое значение имеет исследование сопротивления циклическим нагрузкам, скорости роста трещины усталости (СРТУ) и определение соответствующих характеристик [2, 3]. Величина СРТУ характеризует главным образом надежность материала, его возможность сохранять работоспособность в условиях имеющегося повреждения в виде трещины усталости некоторого размера [4–10].

При определении характеристик СРТУ существует несколько параметров испытаний, которые могут оказывать влияние на результат; среди основных: температура испытания, коэффициент асимметрии цикла нагружения, частота нагружения [11–16].

В связи с этим большой интерес представляет изучение влияния изменения указанных параметров испытания на характеристики СРТУ жаропрочных титановых сплавов марок ВТ8, ВТ41, ВИТ1, которые являются одними из наиболее перспективных материалов для деталей ГТД [6, 8, 10, 12, 14].

Материалы и методы

Для исследования влияния параметров нагружения на СРТУ изготовлены штамповки из жаропрочных титановых сплавов разных классов: (α+β)-сплав ВТ8-1; псевдо-α-сплав ВТ41 и интерметаллидный орто-сплав ВИТ1. Полуфабрикаты изготавливали по слитковой технологии, принятой для титановых сплавов с использованием серийных лигатур. Для выплавки слитков сплава применяли вакуумно-дуговой переплав. Литые заготовки подвергали горячей обработке давлением – ковке на промежуточную заготовку с последующей изотермической штамповкой, после чего заготовки подвергали термической обработке. Режимы обработки подобрали таким образом, чтобы получить для сплава ВТ41 заготовки с глобулярно-пластинчатой и пластинчатой структурами, а для сплава ВИТ1 – с глобулярной и пластинчато-глобулярной структурами.

Из полученных заготовок изготовили компактные образцы типа «CT» для испытаний на СРТУ при внецентренном растяжении с базовым размером W=40 мм, толщиной B=10 мм и прямым надрезом. Надрез выполняли электроискровым способом, радиус в вершине надреза составлял 0,2 мм.

Температуру испытания выбрали исходя из области применения сплавов (табл. 1). Коэффициенты асимметрии цикла нагружения (R) составили 0,1 и 0,5 (как наиболее часто используемые). Частота испытаний (f) выбрана исходя из возможности датчика раскрытия трещины: 15 (максимальная рабочая частота) и 7 Гц (половина от максимальной частоты). Испытания проводили при комбинировании различных сочетаний указанных факторов нагружения (табл. 1 – цветом выделены применяемые режимы).

Варианты режимов испытаний

Температура испытания, °С

Коэффициент асимметрии цикла нагружения R

при частоте нагружения, Гц

Испытания на СРТУ проведены по методике, соответствующей требованиям стандарта ASTM E647 и РД 50-345–82 [14, 16, 17], на сервогидравлической испытательной машине PSB25 фирмы Schenck. Длину трещины измеряли методом податливости при помощи датчика раскрытия трещины фирмы Schenck. Управление испытанием и сбор данных осуществляли при помощи компьютера со специализированным программным обеспечением.

Для испытаний вначале при комнатной температуре выращивали предварительную трещину при выбранных для каждого испытания постоянной частоте и коэффициенте асимметрии цикла. Размах ΔK коэффициента интенсивности напряжений (КИН) уменьшали по ступенчатому режиму по мере увеличения длины трещины. Нанесение начальной трещины осуществляли до достижения общего приращения длины нанесенной трещины 1,5–2 мм. Для всех испытанных образцов исходная трещина располагалась в плоскости, перпендикулярной направлению действия приложенной силы и имела одинаковую длину по фронту развития. Далее проводили испытания образцов с нанесенной трещиной по режимам, указанным в табл. 1, поддерживая постоянный размах нагрузки ΔР, величина которой превышала приложенную на завершающем этапе при нанесении исходной трещины. При каждом режиме испытывали не менее двух образцов, при выведении средних результатов учитывали рекомендации, изложенные в работе [18].

Результаты

Анализ характера макроразрушений образцов показал, что процесс разрушения происходит строго в направлении от вершины надреза в глубь образца. В целом поверхность разрушения имеет плоский характер и располагается перпендикулярно направлению действия нагрузки. На траектории продвижения трещины усталости отсутствуют выпучивания, сужающие сечение образца перед фронтом трещины и искажающие результаты испытаний, что свидетельствует о корректности проведения испытаний.

По результатам испытаний построили кинетические диаграммы усталостного разрушения (КДУР) [19] с использованием программного обеспечения фирмы Schenck. На диаграммах выделяли линейный участок и анализировали его. Коэффициенты уравнения Пэриса, полученные по результатам обработки, наносили на диаграмму в двойных логарифмических координатах «lgC–lgn» (рис. 1). Видно, что для результатов, полученных при рабочих температурах, 90% значений находятся в интервале значений коэффициентов: n=0,9–4,5 и С=10 -8 ÷10 -14 , а при комнатной температуре 80% результатов находятся в интервале значений: n=4,5–10,5 и С=10 -13 ÷10 -17 . Необходимо отметить, что с увеличением коэффициента n значения C монотонно убывают.

Рис. 1. Параметры уравнения Пэриса (C и n) для исследованных сплавов с типами структур: глобулярной (Г), пластинчатой (П) и глобулярно-пластинчатой (ГП)

Для каждого сплава результаты на диаграмме «lgC–lgn» располагаются в достаточно узких областях (табл. 2).

Интервалы значений коэффициента nдля исследованных сплавов

Интервал значений коэффициента n для сплавов

Для всех сплавов при прочих равных условиях значения коэффициента n при рабочих температурах ниже, чем при комнатной температуре. Для сплава ВТ8-1 наименьшая разница между значениями n при разных температурах испытаний, для сплава ВИТ1 – разница наибольшая.

На диаграмме «lgC–lgn» результаты расположены так, что можно предположить, что они подчиняются общей зависимости. Такая закономерность отмечена в нескольких работах [18, 20–25], в большинстве из которых, также как и в работах [19, 21], для никелевых сплавов предложена гипотеза, что коэффициенты уравнения Пэриса описываются прямой линией в полулогарифмических координатах – в основном для значений коэффициента n, находящихся в интервале 1,5–4. Для титановых сплавов, исследованных в данной работе, эта зависимость не подходит. Однако в двойных логарифмических координатах данные хорошо аппроксимируются прямой линией (рис. 2), описываемой функцией lgC= a + b ·lgn (коэффициенты уравнения составляют а =3·10 -7 , b =-9,155). Всего обработана 21 точка, коэффициент корреляции достаточно высокий – R 2 =0,95.

Необходимо отметить, что этой зависимостью описываются результаты для сплавов различных классов, испытанных при различных температурах и коэффициентах асимметрии, исследованных в данной работе.

Как известно, испытания на определение СРТУ – достаточно сложны и при проведении таких испытаний очень многое зависит от опыта исследователя. Поэтому одним из важных вопросов является определение критерия, подтверждающего, что полученные результаты корректны, поскольку при проведении испытания и обработке результатов всегда имеет место субъективная оценка исследователя.

Как отмечалось ранее, полученные в этой работе данные по коэффициентам уравнения Пэриса для всех исследованных жаропрочных титановых сплавов при различных температурах испытаний и коэффициентах асимметрии цикла нагружения достаточно хорошо аппроксимируются прямой линией в двойных логарифмических координатах (рис. 2). В связи с этим можно предположить, что соответствие (с определенным допущением) получаемых коэффициентов уравнения Пэриса описанной ранее зависимости может быть справедливо для всех жаропрочных титановых сплавов и служить критерием корректности полученных характеристик.

Для проверки этого предположения на диаграмму «lgC–lgn» к полученным в работе результатам нанесены данные из литературных источников для сплавов ВТ8-1 [26], ВТ25У [26], IMI 834 [27], Ti64 [28, 29], Ti6242 [30], Timetal 834 [31]. Диаграмма приведена на рис. 3. Видно, что результаты, полученные из литературных источников, хорошо согласуются с выдвинутым предположением. Общий массив данных по-прежнему хорошо аппроксимируется прямой линией.

Таким образом, можно предположить, что указанную зависимость можно использовать для проверки корректности результатов испытаний, а также корректности нахождения средних результатов.

Обсуждение и заключения

1. Установлено, что параметры уравнения Пэриса (C и n) для исследованных жаропрочных титановых сплавов не являются независимыми и аппроксимируются общей прямой линией в координатах «lgC–lgn».

2. Гипотезу о линейной зависимости между коэффициентами уравнения Пэриса в двойных логарифмических координатах можно использовать для проверки корректности полученных результатов для жаропрочных титановых сплавов.

О расчете скорости роста усталостной трещины Текст научной статьи по специальности « Физика»

Аннотация научной статьи по физике, автор научной работы — Воробьев А. З.

Изложена методика расчета скорости роста усталостной трещины при сложных программах нагружения растяжением. Основой расчета являются уравнение Пэриса Эрдогана и эмпирическая формулa, которая определяет «торможение» развития трещины при действии наиболее высоких нагрузок программы нагружения. Приведено сравнение результатов расчета с данными эксперимента на полосе из сплава АК4-1Т1.

Похожие темы научных работ по физике , автор научной работы — Воробьев А. З.

Текст научной работы на тему «О расчете скорости роста усталостной трещины»

УЧЕНЫЕ ЗАПИСКИ Ц А Г И То м VI 1975

О РАСЧЕТЕ СКОРОСТИ РОСТА УСТАЛОСТНОЙ ТРЕЩИНЫ

Изложена методика расчета скорости роста усталостной трещины при сложных программах нагружения растяжением. Основой расчета являются уравнение Пэриса — Эрдогана и эмпирическая формула, которая определяет .торможение» развития трещины при действии наиболее высоких нагрузок программы нагружения. Приведено сравнение результатов расчета с данными эксперимента на полосе из сплава АК4-1Т1.

Учет особенностей развития усталостной трещины при нестационарном нагружении является одной из главных задач при определении долговечности конструкций, поврежденных трещинами.

В настоящее время наметилось три пути решения этой задачи:

— подробное изучение закономерностей развития трещин при различных случаях чередования нагрузок и, далее, создание точных методов расчета;

— создание простых моделей механизма роста трещин, удобных для расчета;

— разработка методик расчета, базирующихся на результатах феноменологических исследований.

Последнему подходу к решению этой задачи посвящена данная работа. Методика расчета скорости роста трещин опирается на экспериментальные данные о торможении этого роста редкими высокими нагрузками. Предполагается, что размер трещины определяете одной характеристикой — ее длиной и, что при стационарном нагружении связь скорости роста трещины с ее длиной, уровнем и асимметрией напряжений подчиняется соотношению Пэриса — Эрдогана:

где ДАТ — размах коэффициента интенсивности напряжения; /? — коэффициент асимметрии; с, т и q — эмпирические константы; формула Пэриса — Эрдогана, а также излагаемый ниже метод расчета скорости роста трещин применимы при /?> — 0,2; малые нагрузки не влияют на рост трещин при больших нагрузках; влияние средних нагрузок на рост трещин при меньших нагрузках пренебрежимо мало в сравнении с аналогичным влиянием высоких нагрузок; тормозящее действие высоких нагрузок можно учесть введением эмпирического коэффициента ст в формулу (1):

Большинство этих предположений отражает современные представления о закономерностях развития усталостных трещин. Последнее положение является результатом выполненного в данной работе эксперимента.

Исследовался рост трещин в образцах из листов алюминиевого сплава .АК4-1Т1 (фиг. 1). Испытания проводились на низкочастотной (0,2 Гц) механической испытательной машине. Специальное электромеханическое устройство обеспечивало реализацию различных программ чередования нагрузок. Измерение длины усталостных трещин выполнялось автоматически с помощью фольговых датчиков трещин и комплекта регистрирующей аппаратуры. На каждом режиме нагружения испытывалось четыре-пять образцов; измерялось приращение длины трещины I (суммы длин по обе стороны центрального надреза) от 1 до 5 мм. За скорость роста трещин на каждом режиме принимались срединные значения (медианы) для интервала Д/ = 0,5 мм (от 1 до 1,5 мм, от 1,5 до 2 мм и т. д.).

Результатом испытаний при стационарном нагружении было определение постоянных т и ? в формулах (1) и (2)

Методика расчета по приведенным значениям; скорости удобна для программ со сложными последовательностями чередования различных нагрузок. Расчет реальной последовательности нагрузок всегда можно привести к определенным характерным периодам действия нагрузок (д^я самолета это полет, либо,: например, 100 ч налета и т. п.). В таких последовательностях элементарные ^иклы нагрузок имеют различную асимметрию и случайный характер чередования. В этих случаях ст определяется по разности максимальных нагрузок циклов*, так как эффект торможения определяется действием остаточных напряжений в пластической зоне у конца трещины; выделение элементарных циклов целесообразно производить по методу „полных циклов” [2].

Проверка изложенной методики расчета развития трещины производилась на образцах из сплава АК4-1Т1 (см. фиг. 1) при трех вариантах программ нагружения. Первый вариант представлял программный цйкл из 624 элементарных циклов трех-четырех ступеней, чередующихся в квазислучайной последовательности. Распределение этих ступеней показано на фиг. 2. Первая ступень включала нагрузки, соответствующие напряжениям цикла: атах = 20 и 24 кг/мм2; оШщ = 6 и 10 кг/мм2; вторая — итах = 16 и 20 кг/мм2; аш.ш = 2 и/6 кг/мм2; третья — ошах=16 кг/мм2; ®Ш|П = 0 и 2 кг/мм2; четвертая—атах = 14 кг/мм2; ®т,п = 0. Испьь тывалось 10 различных вариантов выбранной „случайной» последовательности этих ступеней. Отношение расчетных к экспериментальным величинам скоростей роста трещин по их длине приведено на фиг. 2. При расчете применялся метод „группировки» — все циклы одной ступени (в пределах одного программного цикла) считались действующими подряд.

Второй вариант включал две серии испытаний,; в которых программные циклы различались только по уровням напряжений (аБ=0,8®А). Программный цикл представлял „квазислучайную” последовательность четырех ступеней (см. фиг. 3, а). Расчет выполнялся как по методу „полных циклов», так и путем группировки всех циклов одной ступени в пределах программного цикла Нафиг.З. аг даны экспериментальная и расчетные кривые роста трещин, свидетельствующие

о большей „надежности* расчета по „полным циклам;.

зб — наибольшее ашах за принятый период.

Вариант программы п-5 п=12 71*31 п=30

бщах &тах ъ ■ атш бщах &тах ®т’ш

А7 24,0 12,0 20,0 7,0 16,0 10,0 12,0 0

Б 13,2 9,6 16,0 5,6 12,8 8,0 9,6 0

О 2 Ч 6 8 10 12

Число циклод роста трещины

Вариант программы б, 5г 5Ч Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

1. Porter Т. R. Metod of analysis and prediction for variable amplitude fatigue crack growth, EFM, vol. 4, 1972.

2. С л о 0 и н Б. 3., Трофимов О. Ф. Статистический анализ измерений случайной нагруженности для оценки накопления усталостных повреждений. Вестник машиностроения, 1966, № 10.