Движение тела с переменной массой. Уравнение Мещерского. Формула Циолковского
Вы будете перенаправлены на Автор24
Уравнение движения тела с переменной массой
Под переменной массой будем понимать массу тел, которая при медленном движении тел меняется за счет потери или приобретения вещества.
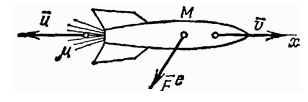
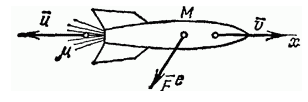
Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Принцип действия ракеты очень прост. Ракета с большой скоростью выбрасывает вещество (газы), воздействуя на него с большой силой. Выбрасываемое вещество с той же, но противоположно направленной силой в свою очередь действует на ракету и сообщает ей ускорение в противоположном направлении. На ракету действуют внешние силы: сила земной тяжести, гравитационное притяжение Солнца и планет, а также сила сопротивления среды, в которой движется ракета.
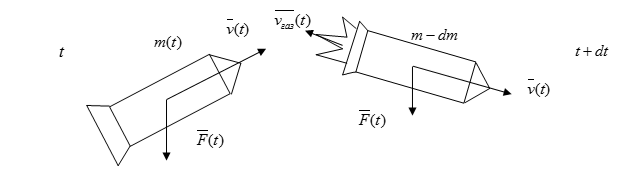
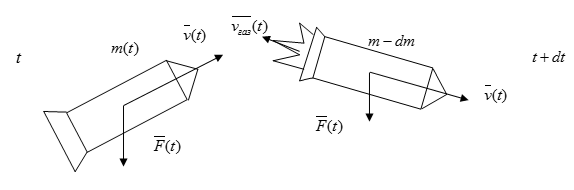
Пусть $m(t)$- масса ракеты в произвольный момент времени $t$, а $v(t)$- ее скорость в тот же момент. Количество движения ракеты в этот момент времени будет $mv$. Спустя время $dt$ масса и скорость ракеты получат приращение $dm$ и $dv$ (величина $dm$ отрицательна). Количество движения ракеты станет равным $(m+dm)(v+dv)$. Сюда надо добавить количество движения газов, образовавшихся за время $dt$. Оно равно $dm_ <газ>v_ <газ>$, где $dm_ <газ>$- масса газов, образовавшихся за время $dt$, а $v_ <газ>$- их скорость. Вычитая из суммарного количества движения в момент $t+dt$ количество движения системы в момент времени $t$, найдем приращение этой величины за время $dt$. Это приращение равно $Fdt$, где $F$- геометрическая сумма всех внешних сил, действующих на ракету. Таким образом:
Время $dt$ и приращения $dm$ и $dv$ устремим к нулю, т.к. нас интересуют предельные отношения или производные $dm/dt$ и $dv/dt$. Поэтому, раскрывая скобки, можно отбросить произведение $dm\cdot dv$, как бесконечно малую высшего порядка. Далее, ввиду сохранения массы, $dm+dm_ <газ>=0$. Пользуясь этим, можно исключить массу газов $dm_ <газ>$. А разность $v_ <отн>=v_ <газ>-v$ есть скорость истечения газов относительно ракеты — скорость газовой струи. С учетом этих замечаний уравнение (1) преобразуется к виду:
Готовые работы на аналогичную тему
Разделив на $dt$, получаем:
Уравнение Мещерского
По форме уравнение (3) совпадает с уравнением, выражающим второй закон Ньютона. Однако масса тела $m$здесь не постоянна, а меняется во времени из-за потери вещества. К внешней силе $F$ добавляется дополнительный член $v_ <отн>\frac
Формула Циолковского
Применим уравнение (2) к движению ракеты, на которую не действуют никакие внешние силы. Полагая $F=0$, получим:
Допустим, что ракета движется прямолинейно в направлении, противоположном скорости газовой струи $v_ <отн>$. Если направление полета принять за положительное, то проекция вектора $v_ <отн>$ на это направление будет отрицательной и равной $-v_ <отн>$. Поэтому в скалярной форме предыдущее уравнение можно записать так $mdv=v_ <отн>dm$. Тогда:
Скорость газовой струи $v_ <отн>$ может меняться во время полета. Однако простейшим и наиболее важным является случай, когда она постоянна. Предположение о постоянстве сильно облегчает решение уравнения (4). В этом случае:
Значение постоянной интегрирования С определяется начальными условиями. Допустим, что в начальный момент времени скорость ракеты равна нулю, а ее масса равна $m_ <0>$. Тогда из предыдущего уравнения получаем:
Последнее соотношение называется формулой Циолковского.
Формула Циолковского позволяет рассчитать запас топлива, необходимый, чтобы сообщить ракете скорость $\upsilon $.
Величина достигаемой ракетой максимальной скорости не зависит от времени сгорания топлива.
Оптимальным путем изменения достигаемой максимальной скорости является увеличение относительной скорости истечения газов.
Для получения первой космической скорости при меньшем соотношении между массой ракеты и требуемой массы топлива целесообразно использование многоступенчатых ракет.
Примеры
Космический корабль двигался с постоянной по величине скоростью $v$. Для изменения направления его полета включается двигатель, выбрасывающий струю газа со скоростью $v_ <отн>$ относительно корабля в направлении, перпендикулярном к его траектории. Определить угол $\alpha $, на который повернется вектор скорости корабля, если начальная масса его $m_ <0>$, а конечная $m$.
Решение:
Ускорение корабля по абсолютной величине равно:
$a=\omega ^ <2>r=\omega v$, причем $v=const$. Поэтому уравнение движения:
$m\frac
Так как $d\alpha =\omega dt$ есть угол поворота за время $dt$, интегрируя наше уравнение, получим:
Ответ: угол поворота вектора скорости равен: $\alpha =\frac
Ракета перед стартом имеет массу $m_ <0>=250$кг. На какой высоте окажется ракета через $t=20$с после начала работы двигателей? Расход топлива равен $\mu =4$кг/с и скорость истечения газов относительно ракеты $v_ <отн>$$=1500$м/с постоянны. Поле тяготения Земли считать однородным.
Дано: $m_ <0>=250$кг, $t=20$с, $\mu =4$кг/с, $v_<отн>=1500$м/с.
Решение:
Запишем уравнение Мещерского в однородном поле тяготения Земли в виде:
где $m=m_ <0>-\mu t$, а $v_ <0>$- скорость ракеты в момент времени $t$. Разделяя переменные получаем:
Решение данного уравнения, удовлетворяющего начальному условию $v_ <0>=0$ при $t=0$, имеет вид:
Учитывая что $H_ <0>=0$ при $t=0$ получим:
Подставляя начальные значения, получаем:
Ответ: через $20$с ракета окажется на высоте $H=3177,5$м.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 06 04 2021
Движение тела с переменной массой
Для начала сформулируем, что такое переменная масса.
Переменная масса – это масса тела, которая может меняться при медленных движениях из-за частичных приобретений или потерь составляющего вещества.
Уравнение движения материальной точки с переменной массой
Чтобы записать уравнение движения для тела с такой массой, возьмем для примера движение ракеты. В основе ее перемещений лежит очень простой принцип: она движется за счет выброса вещества с большой скоростью, а также сильного воздействия, оказываемого на это вещество. В свою очередь выбрасываемые газы также оказывают воздействие на ракету, придавая ей ускорение в противоположном направлении. Кроме того, ракета находится под действием внешних сил, таких, как гравитация Солнца и других планет, земная тяжесть, сопротивление среды, в которой она совершает движение.
Обозначим массу ракеты в какой-либо момент времени t как m ( t ) , а ее скорость как v ( t ) . То количество движения, которая она при этом совершает, будет равно m v . После того, как пройдет время d t , обе эти величины получат приращение (соответственно d m и d v , причем значение d m будет меньше 0 ). Тогда количество движения, совершаемого ракетой, станет равно:
( m + d m ) ( v + d v ) .
Нам необходимо учитывать тот момент, что за время d t также происходит движение газов. Это количество тоже нужно добавить в формулу. Оно будет равно d m г а з v г а з . Первый показатель означает массу газов, которые образуются за указанное время, а второй – их скорость.
Теперь нам нужно найти разность между суммарным количеством движения за время t + d t и количеством движения системы во время t . Так мы найдем приращение данной величины за время d t , которое будет равно F d t (буквой F обозначена геометрическая сумма всех тех внешних сил, которые действуют в это время на ракету).
В итоге мы можем записать следующее:
( m + d m ) ( v + d v ) + d m г а з + v г а з — m v = F d t .
Поскольку нам важны именно предельные значения d m d t , d v d t и их производные, приравняем эти показатели к нулю. Значит, после раскрытия скобок произведение d m · d v может быть отброшено. С учетом сохранения массы получим:
d m + d m г а з = 0 .
Теперь исключим массу газов d m г а з и получим скорость, с которой газы будут покидать ракету (скорость струи вещества), выражающаяся разностью v о т н = v г а з — v . Учитывая эти преобразования, можно переписать исходное уравнение в следующем виде:
d m v = v о т н d m + F d t .
Теперь разделим его на d t и получим:
m d v d t = v о т н d m d t + F .
Уравнение Мещерского
Форма полученного уравнения точно такая же, как у уравнения, выражающего второй закон Ньютона. Но, если там мы имеем дело с постоянной массой тела, то здесь из-за потери вещества она постепенно меняется. К тому же помимо внешней силы нужно учитывать так называемую реактивную силу. В примере с ракетой это будет сила выходящей из нее газовой струи.
Уравнение m d v d t = v о т н d m d t + F впервые вывел русский механик И.В. Мещерский, поэтому оно получило его имя. Также его называют уравнением движения тела с переменной массой.
Формула Циолковского
Попробуем исключить из уравнения движения ракеты внешние силы, воздействующие на нее. Предположим, что движение ракеты прямолинейно, а направление противоположно скорости газовой струи v о т н . Будем считать направление полета положительным, тогда проекция вектора v о т н является отрицательной. Она будет равна — v о т н . Переведем предыдущее уравнение в скалярную форму:
m d v = v о т н d m .
Тогда равенство примет вид:
d v d m = — v о т н m .
Газовая струя может выходить во время полета с переменной скоростью. Проще всего, разумеется, принять ее в качестве константы. Такой случай наиболее важен для нас, поскольку так уравнение решить намного проще.
Исходя из начальных условий, определим, какое значение приобретет постоянная интегрирования С. Допустим, что в начале пути скорость ракеты будет равна 0 , а масса m 0 . Следовательно, из предыдущего уравнения можем вывести:
C = v о т н ln m 0 m .
Тогда мы получим соотношения следующего вида:
v = v о т н ln m 0 m или m 0 m = e v v о т н .
Это соотношение и является формулой Циолковского.
Она предназначена для расчета запаса топлива, с помощью которого ракета может набрать необходимую скорость. При этом время сгорания топлива не обусловливает величину максимальной скорости ракеты. Чтобы разогнаться до предела, нужно увеличить скорость истечения газов. Для достижения первой космической скорости следует изменить конструкцию ракеты. Она должна быть многоступенчатой, поскольку необходимо меньшее соотношение между требуемой массой топлива и массой ракеты.
Разберем несколько примеров применения данных построений на практике.
Условие: у нас есть космический корабль, скорость которого постоянна. Для изменения направления полета в ней нужно включить двигатель, который выбрасывает газовую струю со скоростью v о т н . Направление выброса перпендикулярно траектории корабля. Определите угол изменения вектора скорости при начальной массе корабля m 0 и конечной m .
Решение
Ускорение по абсолютной величине будет равно a = ω 2 r = ω v , причем v = c o n s t .
Значит, уравнение движения будет выглядеть так:
m d v d t = v о т н d m d t перейдет в m v ω d t = — v о т н d m .
Поскольку d a = ω d t является углом поворота за время d t , то после интеграции первоначального уравнения получим:
a = v о т н v ln m 0 m .
Ответ: искомый угол будет равен a = v о т н v ln m 0 m .
Условие: масса ракеты перед стартом равна 250 к г . Вычислите высоту, которую она наберет через 20 секунд после начала работы двигателя. Известно, что топливо расходуется со скоростью 4 к г / с , а скорость истечения газов постоянна и равна 1500 м / с . Поле тяготения Земли можно считать однородным.
Решение
Начнем с записи уравнения Мещерского. Оно будет иметь следующий вид:
m ∆ v 0 ∆ t = μ v о т н — m g .
Здесь m = m 0 — μ t и v 0 – скорость ракеты в заданный момент времени. Разделим переменные:
∆ v 0 = μ v о т н m 0 — μ t — g ∆ t .
Теперь решим полученное уравнение с учетом первоначальных условий:
v 0 = v о т н ln m 0 m 0 — μ t — g t .
С учетом того, что H 0 = 0 при t = 0 , у нас получится:
H = v о т н t — g t 2 2 + v о т н m 0 μ 1 — μ t m 0 ln 1 — μ t m 0 .
Добавим заданные значения и найдем ответ:
H = v о т н t — g t 2 2 + v о т н m 0 μ 1 — μ t m 0 ln 1 — μ t m 0 = 3177 , 5 м .
Ответ: через 20 секунд высота ракеты будет составлять 3177 , 5 м .
Уравнение движения тел с переменной массой
Й и 3-й з-ны Ньютона
Второй закон Ньютона — основной закон динамики поступательного движения — отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.
Если рассмотреть действие различных сил на одно и то же тело, то оказывается, что ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующей приложенных сил:
При действии одной и той же силы на тела с разными массами их ускорения оказываются различными, а именно:
Используя выражения (6.1) и (6.2) и учитывая, что сила и ускорение — величины векторные, можем записать
Соотношение (6.3) выражает второй закон Ньютона:ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
В СИ коэффициент пропорциональности k = 1. Тогда
a = F/m,
F = ma = mdv/dt (6.4)
Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (6.4) ее можно внести под знак производной:
F=(d/dt)(mv). (6.5)
p = mv, (6.6)
численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения)этой материальной точки.
Подставляя (6.6) в (6.5), получим
F=dp/dt (6.7)
Это выражение — более общая формулировка второго закона Ньютона:скорость изменения импульса материальной точки равна действующей на нее силе. Выражение (6.7) называется уравнением движения материальной точки.
Единица силы в СИ — ньютон(Н): 1 Н — сила, которая массе в 1 кг сообщает ускорение 1 м/с 2 в направлении действия силы:
Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго. Действительно, в случае равенства нулю равнодействующей сил (при отсутствии воздействия на тело со стороны других тел) ускорение (см. (6.3)) также равно нулю. Однако первый закон Ньютона рассматривается как самостоятельный закон (а не как следствие второго закона), так как именно он утверждает существование инерциальных систем отсчета, в которых только и выполняется уравнение (6.7).

Если на материальную точку действует одновременно несколько сил, то, согласно принципу независимости действия сил, под F во втором законе Ньютона понимают результирующую силу.
Третий закон Ньютона
Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона:всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
где F12 — сила, действующая на первую материальную точку со стороны второй; F21 — сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
При использовании законов динамики иногда допускают следующую ошибку: так как действующая сила всегда вызывает равную по модулю и противоположную по направлению силу противодействия, то, следовательно, их равнодействующая должна быть равна нулю и тела вообще не могут приобрести ускорения. Однако надо помнить, что во втором законе Ньютона речь идет об ускорении, приобретаемом телом под действием приложенных к нему сил. Равенство нулю ускорения означает равенство нулю равнодействующей сил, приложенных к одному и тому же телу. Третий же закон Ньютона говорит о равенстве сил, приложенных к различным телам. На каждое из двух взаимодействующих тел действует только одна сила, которая и сообщает данному телу ускорение.
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
6. Импульс. З-н сохр. импульса
Векторная величина p = mv, (6.6) численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения)этой материальной точки.

Это выражение и является законом сохранения импульса:импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон сохранения импульса — фундаментальный закон природы.
В механике Галилея — Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс. Центром масс(или центром инерции)системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен
где mi и ri — соответственно масса и радиус-вектор i-й материальной точки; n — число материальных точек в системе;
Скорость центра масс
Учитывая, что pi =mivi, а
есть импульс р системы, можно написать
p = mvc, (9.2)
т. е. импульс системы равен произведению массы системы на скорость ее центра масс.
Подставив выражение (9.2) в уравнение (9.1), получим
mdvc/dt=F1+ F2+. + Fn, (9.3)
т. е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Выражение (9.3) представляет собой закон движения центра масс.
В соответствии с (9.2) из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
Уравнение движения тел с переменной массой
Движение некоторых тел сопровождается изменением их массы, например масса ракеты уменьшается за счет истечения газов, образующихся при сгорании топлива, и т. п.
Выведем уравнение движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты т, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm
и станет равной т-dm, а скорость станет равной v+dv. Изменение импульса системы за отрезок времени dt
dp = [(m-dm) (v+dv)+dm (v + u)]- mv,
где и — скорость истечения газов относительно ракеты. Тогда
dp = mdv + udm
(учли, что dm dv — малый высшего порядка малости по сравнению с остальными).
Если на систему действуют внешние силы, то dp = Fdt, поэтому
Fdt = mdv + udm,
mdv/dt=F—udm/dt. (10.1)
Член —udm/dt называют реактивной силой
Fp. Если u противоположен v, то ракета ускоряется, а если совпадает с v, то тормозится.
Таким образом, мы получили уравнение движения тела переменной массы
ma=F + Fp, (10.2)
которое впервые было выведено И. В.Мещерским (1859—1935).
Идея применения реактивной силы для создания летательных аппаратов высказывалась в 1881 г. Н. И. Кибальчичем (1854—1881). К.Э.Циолковский (1857— 1935) в 1903 г. опубликовал статью, где
предложил теорию движения ракеты и основы теории жидкостного реактивного двигателя. Поэтому его считают основателем отечественной космонавтики.
Применим уравнение (10.1) к движению ракеты, на которую не действуют никакие внешние силы. Полагая F = 0 и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим
dv dm т dv/dt=-udm/dt. откуда
Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а ее стартовая масса то, то С = uln m0. Следовательно,
Это соотношение называется формулой Циолковского.Она показывает, что: 1) чем больше конечная масса ракеты т, тем больше должна быть стартовая масса ракеты то; 2) чем больше скорость истечения и газов, тем больше может быть конечная масса при данной стартовой массе ракеты.
Выражения (10.2) и (10.3) получены для нерелятивистских движений, т. е. для случаев, когда скорости v и u малы по сравнению со скоростью света с.
http://zaochnik.com/spravochnik/fizika/osnovy-dinamiki/dvizhenie-tela-s-peremennoj-massoj/
http://lektsii.org/8-81702.html