Уравнение как математическая модель в школьном курсе математики
Разделы: Математика
Класс: 9
Практически все изучаемые математическими представлениями явления и процессы в конечном итоге сводятся к нахождению решений уравнений или систем уравнений различной степени сложности. Учащиеся школ с самого начала изучения математики решают уравнения даже в самых простых ситуациях. Любая математическая задача представляет собой проблему нахождения неизвестной величины, зависящей от набора параметров с известными значениями. Простые арифметические задачи предполагают определение какого-либо значения путём выполнения основных арифметических действий с известными величинами, что означает решение уравнений.
На современном этапе развития информационных технологий с самых азов обучения совершенно необходимо развивать у обучаемых способности создавать абстрактные представления конкретных явлений и процессов в виде математических формул (по сути уравнений) с последующим определением способов вычисления значений параметров этих формул путём решения соответствующих уравнений методами программирования. То есть для решения даже самых простых задач в современных условиях надо научить школьников разрабатывать рабочие программы. Хорошо известно, что в основе разработки любой программы лежит алгоритм, моделирующий то или иное явление или процесс. Причём это заключение распространяется не только на математические области исследований, но и на все другие научные дисциплины.
Таким образом, для решения любого уравнения в самом начале надо разработать алгоритм процесса этого решения.
При разработке алгоритма решения задач прежде всего необходимо обозначить заключения и направления рассуждений, известные значения данных и искомые значения переменных, находить в базе данных признаки индивидуальные и общие, уделить достаточное внимание противопоставлению и сопоставлению фактов.
На начальном этапе изучения математических дисциплин учащимся обычно предлагаются для решения задачи в текстовом виде, преобразование условий которых в вид аналитических формул является достаточно эффективным средством для усвоения школьниками понятий, методов и даже математических теорий как строго формализованных построений. Такой приём является наиболее действенным средством развития логического мышления учеников и открывает возможности для воспитания математического восприятия изучаемых явлений и даёт возможность учащимся развивать умения и навыки применениях математики на практике [1].
На школьном этапе математического образования для большей наглядности учащимся полезно предлагать применение математического моделирования для решения задач, условия которых описывает конкретные жизненные ситуации, так как соответствующие уравнения наиболее просто ассоциировать с алгебраической или аналитической моделью изучаемых явлений. Подобные задачи позволяют, помимо перечисленного выше, усвоить учащимся понятия таких логических операций, как обобщение, классификация, анализ через синтез, сравнение, которые способствуют его развитию логического мышления.
На более поздних этапах обучения можно начинать создание математических моделей не только обычных алгебраических уравнений, а перейти к моделированию процессов, которые описываются в аналитическом виде с использованием понятий функций одной или нескольких переменных, а в выпускных классах даже дифференциальных уравнений. Наиболее интересующимся математикой ученикам можно предлагать моделировать неравенства, а также системы уравнений и системы неравенств и т.п. Таким образом, разработка математических моделей сопровождается приобретением школьниками навыков в умении перевода условий практических задач на язык алгебры или математического анализа [2, 3].
Для углубления знаний школьников полезно изучить процессы моделирования математических объектов, представленных самыми разными математическими формами, такими, как таблицы объектные и числовые, формулы числовые и буквенные, функции, уравнения алгебраические и дифференциальные и их системы, неравенства, системы неравенств, математические ряды, геометрические формы, различные схемы, диаграммы, графы и пр.
При разработках математических моделей используются алгоритмы явлений и процессов, изображаемые в виде отрезков, направленных отрезков, ломаных и кривых линий, геометрических фигур, числовых лучей, схем, значков и т.п. Такие представления алгоритмов называются блок-схемами алгоритмов. Существует перечень специальных знаков элементов блок-схем, унифицированный в математической литературе. Эти знаки обозначают постоянные параметры, переменные, базы данных, математические действия, логические операторы, последовательность и направления расчётов, функционалы и т.п. операции. Такая унификация позволяет наглядным образом представлять блок-схемы алгоритмов в виде, понятном специалистам.
Согласно [4], математическое моделирование представляет собой «способ, инструмент, научный прием изучения окружающего мира».
Как указывалось выше, этот процесс заключается в описании исследуемых явлений, процессов, объектов и систем самой разной природы на математическом языке с применением соответствующих понятий, обозначений и функционалов. При этом важно показать зависимость степени сложности разрабатываемых математических моделей от предполагаемой детализации исследования поставленной задачи, поставленной цели исследования, и, конечно же, степени математической подготовки и уровня знаний школьника о моделируемом объекте.
В самом простом виде процесс моделирования выглядит следующим образом: реальный объект замещается моделью. Затем строится алгоритм процесса или явления, на его основе разрабатывается компьютерная программа, и уже эта программа служит объектом проведения экспериментов и исследований, результаты которых ложатся в основу выводов о проведённых исследованиях самого оригинального объекта.
Очень важно показать и добиться твёрдого усвоения школьниками того факта, что математическое моделирование в определённых ситуациях является единственным способом изучения сложных объектов, аналитические представления которых не имеют числовых решений, или таких, с которыми невозможно проводить прямые эксперименты в силу их размеров (мегаобъекты и нано-объекты), невозможности или опасности последствий вмешательства в их функционирование (экономические процессы и экологические системы). Необходимо продемонстрировать возможность математического моделирования существенно сокращать время исследования реального объекта, принимая время как переменный параметр.
Кроме этого, в результате обучения ученики должны усвоить основные приёмы математического моделирования явлений, объектов и процессов, типы, этапы, классификации решаемых задач, научиться преобразовывать математические модели одного класса в модели другого класса и т.п.
В качестве примера разработки математической модели уравнения рассмотрим решение несложной алгебраической задачи согласно рекомендациям работы [5].
Задача. Необходимо определить скорость моторной лодки, если известно, что она двигалась равномерно параллельно направлению равномерного движения теплохода, при этом её скорость в три раза превышала скорость теплохода и, стартовав на один час позже теплохода с того же причала, моторная лодка за два часа пути проплыла расстояние на 24 км больше, чем теплоход.
Создадим математическую модель задачи:
Теперь осталось решить уравнение, составленное на основе математической модели:
х = 8, и скорость моторной лодки:
Ответ: скорость моторной лодки равна 24 км/ч.
Таким образом, показано практическое применение процесса решения задачи с помощью разработки математической модели движения моторной лодки и теплохода путём разработки блок-схемы алгоритма процесса, который может быть основой для написания компьютерной программы решения этой задачи при различных значениях параметров движения этих судов.
Статья «Уравнения и неравенства как математические модели»
Математическая статистика − наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала (например, оценить необходимый объем выборки для получения результатов требуемой точности при выборочном обследовании). Любой творчески работающий специалист физического воспитания в ходе своей работы получают фактический экспериментальный материал (первичный цифровой массив). Если эти данные не будут корректно обработаны с помощью методов математической статистики, то их работа теряет всякий теоретический и практический смысл.
Просмотр содержимого документа
«Статья «Уравнения и неравенства как математические модели»»
уравнения и неравенства как математические модели
1.Примеры решения уравнений с параметрами как математической модели………………………………………………………………………..
1.1.Вид соотношений с выделенными параметрами……………………
1.2. Пример решения неравенства с параметром…………………….
Математическая статистика − наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала (например, оценить необходимый объем выборки для получения результатов требуемой точности при выборочном обследовании). Любой творчески работающий специалист физического воспитания в ходе своей работы получают фактический экспериментальный материал (первичный цифровой массив). Если эти данные не будут корректно обработаны с помощью методов математической статистики, то их работа теряет всякий теоретический и практический смысл.
В настоящее время ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, неравенств и их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.
Цель: проанализировать уравнения и неравенства как математические модели.
Провести теоретический анализ литературы по теме исследования.
примеры решения уравнений с параметрами как математической модели;
вид соотношений с выделенными параметрами;
пример решения неравенства с параметром.
1.Примеры решения уравнений с параметрами как математической модели
Ряд проблем в различных отраслях человеческой деятельности может быть изучен математическими методами. На этом пути, применяя язык математики, изучаемым явлениям ставят в соответствие модельные явления. Если они описаны с помощью математических правил, то такие модели называются математическими. Примером такого процесса является процесс решения простейших так называемых «текстовых» задач с помощью сведения их к уравнениям или неравенствам [7].
Любая предметная область характеризуется своим набором понятий связей между ними. Каждая предметная область имеет свои специфические методы решения задач. Необходимость в формализованном представлении знаний возникла в связи с их обработкой средствами компьютерной техники. Методология моделирования и формализации концептуальных знаний, ориентированная на их компьютерную обработку, является одной из основных тем развития искусственного интеллекта [7].
Под моделью мы будем понимать «систему произвольной природы, отражающую свойства, характеристики и связи моделируемого объекта (объекта-оригинала), которые считаются существенными для решения данной задачи» [5, с. 46]. При этом отсутствие в модели несущественных элементов не менее важно, чем присутствие в ней существенных.
Главное назначение модели состоит в упрощении получения информации о свойствах объекта-оригинала. Полное соответствие модели оригиналу невозможно по определению.
Пример. Рассмотрим уравнение 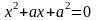
Множество решений такого уравнения – это множество пар чисел, при подстановке которых в уравнение получается верное равенство.
Взгляд относительно х говорит о решении уравнения относительно х. В этом случае аргументы х и а считают неравноправными. Поэтому необходимо выразить при решении х через а, которое называют «параметром».
Можно рассмотреть это уравнение по-другому, взгляд относительно а: необходимо иметь ответ в таком виде, чтобы для каждого значения а было указано, какие числа х в паре с этом а дают решения данного уравнения.
На этом пути, если брать разные основания для классификаций (например, от вида математического выражения, задающего уравнение) и учитывая разные взгляды на аргументы, входящие в это математическое выражение, получим спектр разных типов уравнений (неравенств).
1.1.Вид соотношений с выделенными параметрами
В реальных задачах (например, с физическим содержанием) естественно вводится неравноправие аргументов, входящих в уравнение. Они делятся на «неизвестные», обозначаемые, как правило, последними буквами латинского алфавита (…, x, y, z), и «параметры» – обозначаемые первыми буквами (a, b, c,…) [7].
Рассмотрим один из способов решения задачи с параметрами:
значение параметра (или параметров, если их несколько) считается произвольно фиксированным, и затем ищется решение задачи так, как обычно обращаются с уравнениями и неравенствами с одним неизвестным.
Ответом должно быть перечисление решений для каждого допустимого значения параметра.
Например, ответ при решении неравенства 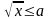
при 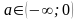
при 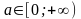
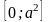
Отметим, что выяснение зависимости решений от значений параметра есть часть процесса решения задачи. Иногда это называют исследованием и отделяют от непосредственного решения. Необходимо запомнить и уяснить, что решение задачи с параметрами без такого этапа не дает решение. Задача нерешена!
1.2.Пример решения неравенства с параметром
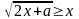
Решение. 1) Находим естественную область определения. Это множество пар 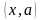
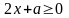

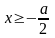
2) Так как 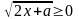
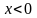
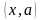
3) Рассмотрим случай 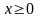
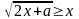

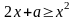

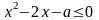
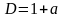
3.1. При 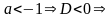
3.2. При 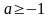
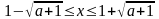
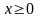
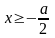
б) первое число больше второго .
Получаем два случая: и .
3.2.1) Пусть . В этом случае из трех исходных чисел самым большим является первое – число 0. Остаются условия 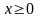
3.2.2) Пусть . Теперь первое число меньше второго и третьего. Сравним второе и третье: 

Это не выполняется ни при каких а. Итак, в этом случае третье число наибольшее. Получили, что 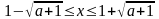
Ответ. 1) если , то решений нет;
2) если , то 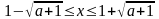
Как уже отмечалось, задачи с параметрами могут бать по-разному классифицированы:
по виду математического выражения (линейные, квадратные и т.д.);
по количеству неизвестных и выражений (системы и т.д.);
по количеству параметров [7].
Выделены и классы методов их решения (формальный, геометрический и др.).
Пример математической модели.
Производственное объединение, в которое входят две мебельные фабрики, нуждается в обновлении парка станков. Причем первой мебельной фабрике нужно заменить три станка, а второй-семь. Заказы можно разместить на двух станкостроительных заводах. Первый завод может изготовить не более 6 станков, а второй завод примет заказ если их будет не мение трех. Требуется определить как размещать заказы [8].
Введем переменные: xij-количество станков, которое будет изготавливать i-й завод для j-й фабрики.
По условию задачи:
Кроме того, должны выполняться условия:
Получаем систему ограничений в форме неравенств и уравнений:
Мы составили математическую модель нашей задачи. Решая систему мы найдем множество различных решений. Вот одно из них:
Оптимальное решение будет зависеть от других параметров, отдаленности заводов, цены на станки и т.д.
Проект «Уравнения и неравенства как математические модели»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
уравнения и неравенства как математические модели
1.1.Вид соотношений с выделенными параметрами……………………
1.2. Пример решения неравенства с параметром…………………….
Математическая статистика − наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала (например, оценить необходимый объем выборки для получения результатов требуемой точности при выборочном обследовании). Любой творчески работающий специалист физического воспитания в ходе своей работы получают фактический экспериментальный материал (первичный цифровой массив). Если эти данные не будут корректно обработаны с помощью методов математической статистики, то их работа теряет всякий теоретический и практический смысл.
В настоящее время ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, неравенств и их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.
Цель: проанализировать уравнения и неравенства как математические модели.
Провести теоретический анализ литературы по теме исследования.
примеры решения уравнений с параметрами как математической модели;
вид соотношений с выделенными параметрами;
пример решения неравенства с параметром.
1.Примеры решения уравнений с параметрами как математической модели
Ряд проблем в различных отраслях человеческой деятельности может быть изучен математическими методами. На этом пути, применяя язык математики, изучаемым явлениям ставят в соответствие модельные явления. Если они описаны с помощью математических правил, то такие модели называются математическими. Примером такого процесса является процесс решения простейших так называемых «текстовых» задач с помощью сведения их к уравнениям или неравенствам [7].
Любая предметная область характеризуется своим набором понятий связей между ними. Каждая предметная область имеет свои специфические методы решения задач. Необходимость в формализованном представлении знаний возникла в связи с их обработкой средствами компьютерной техники. Методология моделирования и формализации концептуальных знаний, ориентированная на их компьютерную обработку, является одной из основных тем развития искусственного интеллекта [7].
Под моделью мы будем понимать «систему произвольной природы, отражающую свойства, характеристики и связи моделируемого объекта (объекта-оригинала), которые считаются существенными для решения данной задачи» [5, с. 46]. При этом отсутствие в модели несущественных элементов не менее важно, чем присутствие в ней существенных.
Главное назначение модели состоит в упрощении получения информации о свойствах объекта-оригинала. Полное соответствие модели оригиналу невозможно по определению.
Пример. Рассмотрим уравнение . Его можно понимать как квадратное уравнение относительно неизвестного х , а можно понимать как квадратное уравнение относительно неизвестного а с параметром х. Следует же понимать это уравнение как уравнение с двумя неизвестными х и а. В левой части уравнения стоит математическое выражение от двух аргументов х и а.
Множество решений такого уравнения – это множество пар чисел, при подстановке которых в уравнение получается верное равенство.
Взгляд относительно х говорит о решении уравнения относительно х. В этом случае аргументы х и а считают неравноправными. Поэтому необходимо выразить при решении х через а, которое называют «параметром».
Можно рассмотреть это уравнение по-другому, взгляд относительно а: необходимо иметь ответ в таком виде, чтобы для каждого значения а было указано, какие числа х в паре с этом а дают решения данного уравнения.
На этом пути, если брать разные основания для классификаций (например, от вида математического выражения, задающего уравнение) и учитывая разные взгляды на аргументы, входящие в это математическое выражение, получим спектр разных типов уравнений (неравенств).
1.1.Вид соотношений с выделенными параметрами
В реальных задачах (например, с физическим содержанием) естественно вводится неравноправие аргументов, входящих в уравнение. Они делятся на «неизвестные», обозначаемые, как правило, последними буквами латинского алфавита (…, x, y, z), и «параметры» – обозначаемые первыми буквами (a, b, c,…) [7].
Рассмотрим один из способов решения задачи с параметрами:
значение параметра (или параметров, если их несколько) считается произвольно фиксированным, и затем ищется решение задачи так, как обычно обращаются с уравнениями и неравенствами с одним неизвестным.
Ответом должно быть перечисление решений для каждого допустимого значения параметра.
Например, ответ при решении неравенства лучше всего записывать в виде:
при решений нет;
при имеем любое х из [7].
Отметим, что выяснение зависимости решений от значений параметра есть часть процесса решения задачи. Иногда это называют исследованием и отделяют от непосредственного решения. Необходимо запомнить и уяснить, что решение задачи с параметрами без такого этапа не дает решение. Задача нерешена!
1.2.Пример решения неравенства с параметром
Решение. 1) Находим естественную область определения. Это множество пар , при которых выражение, задающее задачу определено. Имеем, что .
2) Так как рассмотрим сначала случай . Тогда все пары , входящие в область определения, являются решениями.
3) Рассмотрим случай . Тогда . Исследуем дискриминант получившегося трехчлена. Он равен .
3.1. При действительных решений нет.
3.2. При , решая квадратное неравенство, имеем, что . Однако теперь надо согласовать полученное условие с условиями: и . Это при водит к системе неравенств: Получаем, что х должен быть больше (или равен) каждого из трёх чисел 0, . Поэтому надо знать, как они расположены на числовой оси в зависимости от параметра а. Рассмотрим варианты: а) первое число больше третьего .
б) первое число больше второго .
Получаем два случая: и .
3.2.1) Пусть . В этом случае из трех исходных чисел самым большим является первое – число 0. Остаются условия и .
3.2.2) Пусть . Теперь первое число меньше второго и третьего. Сравним второе и третье: .
Это не выполняется ни при каких а. Итак, в этом случае третье число наибольшее. Получили, что . Объединив все случаи, получим
Ответ. 1) если , то решений нет;
Как уже отмечалось, задачи с параметрами могут бать по-разному классифицированы:
по виду математического выражения (линейные, квадратные и т.д.);
по количеству неизвестных и выражений (системы и т.д.);
по количеству параметров [7].
Выделены и классы методов их решения (формальный, геометрический и др.).
Пример математической модели.
Производственное объединение, в которое входят две мебельные фабрики, нуждается в обновлении парка станков. Причем первой мебельной фабрике нужно заменить три станка, а второй-семь. Заказы можно разместить на двух станкостроительных заводах. Первый завод может изготовить не более 6 станков, а второй завод примет заказ если их будет не мение трех. Требуется определить как размещать заказы [8].
Введем переменные: xij-количество станков, которое будет изготавливать i-й завод для j-й фабрики.
По условию задачи:
x11+x12 
x21+x22 
Кроме того, должны выполняться условия:
Получаем систему ограничений в форме неравенств и уравнений:
x11+x12 
x21+x22 
xij 
Мы составили математическую модель нашей задачи. Решая систему мы найдем множество различных решений. Вот одно из них:
Оптимальное решение будет зависеть от других параметров, отдаленности заводов, цены на станки и т.д.
http://multiurok.ru/files/statia-uravneniia-i-neravenstva-kak-matematicheski.html
http://infourok.ru/proekt-uravneniya-i-neravenstva-kak-matematicheskie-modeli-1203831.html

