Логарифмические уравнения и неравенства
Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
Логарифмическая функция
Определение
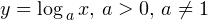
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:
| | a > 1 | 0 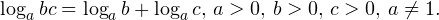 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/> 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:
• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):
Решение логарифмических уравнений и неравенствПример 1. Решите уравнение: Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:
С учетом того, что получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения: На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению: В область допустимых значений входит только первый корень. Ответ: x = 7. Пример 2. Решите уравнение: Решение. Область допустимых значений уравнения определяется системой неравенств:
Очевидно, что эти два условия противоречат друг другу. То есть нет ни одного такого значения x, при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет. Ответ: корней нет. Обратите внимание, что в этом задании нам вообще не пришлось искать корни уравнения. Достаточно оказалось определить, что его область допустимых значений не содержит ни одного действительно числа. Это одно из преимуществ такой последовательности решения логарифмических уравнений и неравенств (начинать с определения области допустимых значений уравнения, а затем решать его путем равносильных преобразований). Примет 3. Решите уравнение: Решение. Область допустимых значений уравнения определяется здесь легко: x > 0. Уравнение принимает вид: Оба ответа входят в область допустимых значений уравнения, поскольку являются положительными числами. Пример 4. Решите уравнение: Решение. Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению: Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению: Первый корень не входит в область допустимых значений уравнения, второй — входит. Ответ: x = -1. Пример 5. Решите уравнение: Решение. Будем искать решения в промежутке x > 0, x≠1. Преобразуем уравнение к равносильному: Оба ответа входят в область допустимых значений уравнения. Пример 6. Решите уравнение: Решение. Система неравенств, определяющая область допустимых значений уравнения, имеет на этот раз вид: Используя свойства логарифма, преобразуем уравнение к равносильному в области допустимых значений уравнению: Используя формулу перехода к новому основанию логарифма, получаем: В область допустимых значений входит только один ответ: x = 4. Перейдем теперь к логарифмическим неравенствам. Это как раз то, с чем вам придется иметь дело на ЕГЭ по математике. Для решения дальнейших примеров нам потребуется следующая теорема: Теорема 2. Если f(x) > 0 и g(x) > 0, то: Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству: Окончательно, с учетом области допустимых значений получаем ответ: Пример 8. Решите неравенство: Решение. Вновь начнем с определения области допустимых значений:
На множестве допустимых значений неравенства проводим равносильные преобразования: После сокращения и перехода к равносильному по теореме 2 неравенству получаем: С учетом области допустимых значений получаем окончательный ответ: Пример 9. Решите логарифмическое неравенство: Решение. Область допустимых значений неравенства определяется следующей системой:
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству: С учетом области допустимых значений получаем окончательный ответ: Пример 10. Решите неравенство: Решение. Область допустимых значений неравенства определяется системой неравенств:
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству: Неравенство будет равносильно двум системам. Первой: Итак, окончательный ответ: II способ. Решаем методом интервалов. Преобразуем неравенство к виду: Вычтем из знаменателя С учетом того, что выражения Множество решений данного неравенства Итак, Итак, что нужно для того, чтобы решать логарифмические уравнения и неравенства?
Главное же требование — это настойчивость в достижении своей цели. Учитесь, тренируйтесь, если нужно — ежедневно, изучайте и запоминайте на примерах основные способы решения неравенств и их систем, анализируйте возникающие ошибки и не допускайте их в будущем. За помощью в этом нелегком деле вы можете обратиться к своему школьному учителю по математике, репетитору, родителям, друзьям и знакомым, книгам, а также огромному количеству материалов, доступных на просторах Интернета. Желаю вам успехов в подготовке к Единому государственному экзамену по математике. АлгебраПлан урока: Задание. Укажите корень логарифмического уравнения Задание. Решите урав-ние В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид Задание. Найдите решение логарифмического уравнения Задание. Решите урав-ние Задание. Решите урав-ние Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания: Уравнения вида logaf(x) = logag(x)Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов. Задание. Решите урав-ние Задание. Найдите корень урав-ния Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями. Задание. Решите урав-ние Получили квадратное уравнение, которое решаем с помощью дискриминанта: Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем: Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4: Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log3 (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3). Уравнения, требующие предварительных преобразованийЕстественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду logaf(x) = logag(x). Задание. Решите урав-ние с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае: Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы: Задание. Решите урав-ние Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем Задание. Решите урав-ние Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log5 5. Тогда урав-ние можно преобразовать: Задание. Решите урав-ние Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что Задание. Решите урав-ние Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log25x 4 к основанию 5, используя известную нам формулу Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы: Логарифмические уравнения с заменой переменныхИногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид. Задание. Решите уравнение методом замены переменной Задание. Найдите решение уравнения методом замены переменной Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части: Логарифмирование уравненийЯсно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры. Задание. Укажите корни урав-ния Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5: Возвращаемся от переменной t к переменной х: Переход от логарифмических неравенств к нелогарифмическимРассмотрим график логарифмической функции у = logax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными. Задание. Найдите решение логарифмического неравенства Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 logas: Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 loga s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения: Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5). Методическая разработка урока «Решение логарифмических уравнений и неравенств» |
| Вложение | Размер |
|---|---|
| statya.doc | 87.5 КБ |
| prilozhenie_1.ppt | 74.5 КБ |
Предварительный просмотр:
УРОК ОБОБЩЕНИЯ И СИСТЕМАТИЗАЦИИ ЗНАНИЙ И СПОСОБОВ ДЕЙСТВИЙ В СОЧЕТАНИИ С ИХ КОМПЛЕКСНЫМ ПРИМЕНЕНИЕМ
В 11 КЛАССЕ ПО ТЕМЕ:
«РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ»
НА ФЕСТИВАЛЬ ПЕДАГОГИЧЕСКИХ ИДЕЙ «ОТКРЫТЫЙ УРОК».
Тема урока: Решение логарифмических уравнений и неравенств
Образовательные: создать условия для повторения и обобщения знаний учащихся по теме «Решение логарифмических уравнений и неравенств», систематизировать способы деятельности учащихся по применению комплекса знаний и способов действий в измененной и новой ситуациях, подготовка к ЕГЭ.
Развивающие: развивать способности применять теоретические знания на практике, развивать навыки работы с тестовыми заданиями, логическое мышление, память, внимание, развивать навыки самоконтроля.
Воспитательные: воспитывать ответственное отношение к изучению математики, трудолюбие, взаимопомощь, волю и настойчивость в достижении поставленной цели.
Тип урока: урок обобщения и систематизации знаний и способов действий в сочетании с их комплексным применением.
Оборудование урока: компьютер, проектор, экран.
- Организация начала занятия.
Учащимся сообщается тема урока и цели, подчеркивается актуальность повторения данной темы для подготовки к ЕГЭ.
Учитель: Ребята, к сегодняшнему уроку я подобрала несколько высказываний известных философов – математиков и даже одного из полководцев. Думаю, что эти слова будут помогать нам в нашей с вами работе. Перед вами слова известного французского философа и математика Рене Декарта: «Недостаточно только иметь хороший разум, но главное — это хорошо применять его».
Наши знания должны работать и принести положительный результат на экзамене. Сегодня каждый из вас проведет диагностику своих знаний по данной теме, для этого у вас имеются диагностические карты, в которых вы оцените свои знания и возможности по каждому из разделов. В соответствии с этой оценкой на индивидуальных консультациях мы постараемся устранить имеющиеся пробелы.
Последуем совету Декарта и используем свои знания в устной работе.
II. Подготовка учащихся к активной учебно-познавательной деятельности на основном этапе урока:
а) актуализация опорных знаний
Учащиеся работают устно по упражнениям, представленным на экране с помощью проектора.
Давайте с вами ещё раз вспомним какие уравнения называются логарифмическими и заострим своё внимание на тех моментах, которые играют немаловажную роль при выполнении заданий.
- Является ли уравнение lg5+xlg6=3 логарифмическим?
- Существует ли хотя бы одно значение x , при котором верно равенство lg(x+3)=lgx+lg3
- Записать область определения логарифмического уравнения log a f(x)=log b g(x) в виде системы неравенств.
- Как решается уравнение, содержащее неизвестное и в основании, и в показателе степени, например x lg x = 10?
- Нужна ли проверка полученных корней при решении логарифмических уравнений, почему? Решить двумя способами уравнение
log 3 (x+6) + log 3 (x-2) = 2 ( два человека на отворотах доски).
в) 7 log 7 x2 =36
л) log 3 x=5log 3 2-2log 3 2
м) log 2 (log 3 x)=1
н) log π (log 3 (log 2 x))=0
7) Что такое логарифмические неравенства? На чем основано решение логарифмических неравенств?
8) Как решаются логарифмические неравенства вида log g(x) f(x)>b, log g(x) f(x)
9) по вариантам решить неравенства (два человека на отворотах доски).
log 0.3 (2x-4) >log 0.3 (x+1)
Оцените свои умения решать простейшие логарифмические уравнения и неравенства.
4. Учащимся предлагается выполнить тест с последующей проверкой. Тест представлен на экране. После выполнения теста на экран выводится слайд с ответами.
первый вариант второй вариант
log 0.5 (x 2 -4x-1) = -2 log 0.5 (x 2 -3x+10) = -3
1) -1 и 5; 2) 5; 3) 5 и -1; 4) -1. 1) 1; 2) 1 и 2; 3) 2; 4)-1и 2.
2.Укажите промежуток, которому принадлежит
log 2 (7+v) — log 2 (1-v) = 2 log 5 (t+5) – log 5 (t-11) = 1
1) [-7 ; -4]; 2) [-4; -1] 3) [-1 ; 2]; 4) [2 ; 5] 1) (-5; 0); 2) (0; 3); 3) (3; 8); 4) (10; 16)
3. Решить неравенство:
log 0.5 (2x+5) > -3 log 0.5 (2x-5)
1) Ø; 2) (-∞; 1,5); 3) (-2,5; 1,5); 4) (-2,5; +∞) 1) Ø; 2) (2,5; 4,5); 3) (4,5; +∞); 4) (-∞; 2,5)
4. Какое из предложенных чисел является решением неравенства:
log √3.5 (x 2 -0,5) √2.5 (x 2 -6,5) > 2
1) -1.9; 2) -√5; 3) 2.3; 4) 5 1) √5/2; 2) 2.7; 3) 3; 4) 3.2
После окончания работы учащиеся сдают тест на отдельных листочках, оставив при этом для проверки номера выбранных ответов. Далее учащимся предоставляется возможность проверить и оценить свою работу.
На экране следующий слайд:
Первый вариант 1 3 3 1
Второй вариант 2 4 3 4
Верно 4 задания — оценка «5»
3 задания — оценка «4»
2 задания — оценка «3»
Другие варианты — «нужно поработать»
III. Закрепление и применение знаний и способов действий.
После того, как вы справились с обязательным уровнем подготовки, предлагаю заняться более интересным делом (цитирую слова Р. Декарта) «Для того, чтобы совершенствовать ум, надо больше размышлять, чем заучивать».
Предлагаю вам поразмышлять над следующими заданиями в группах. Как говориться «одна голова хорошо, а две – лучше».
Каждое ваше правильное решение поможет раскрыть одно мудрое изречение. (Дети работают с карточками в группах по 3-4 человека). Представитель каждой группы дает объяснение решения для всего класса.
На доске постепенно высвечивается высказывание А.В. Суворова «Скорость нужна, а поспешность вредна».
Задания в группах:
1) Решить уравнение:
2) Решить неравенство:
log 2 3-x (x+0.5)/( x (x-1)) ≤ 0
3) Вычислите абсциссу точки пересечения графиков функций:
y = log 0.3 (x 2 — x — 5) и y = log 0.3 (x/3).
б) учащимся предлагается выполнить дифференцированную самостоятельную работу с последующей проверкой.
log 2 0.5 x -log 0.5 x=6
2. Решить неравенство
3/(lgx – 2)+2/(lgx – 3)= -4
2. Решить неравенство
|1-log 1/9 x|+1 = |2- log 1/9 x|
2. Решить неравенство
log 4 2 x + log 4 √x > 1.5
Выполнив работу, учащиеся сдают ее на проверку. На экран выводятся ответы и краткое решение. Учащимся предлагается проверить и оценить свою работу.
Содержание следующего слайда: проверка самостоятельной работы.
1. ОДЗ: x >0, обозначим log 0.5 x=y
Ответ: x 1 = 4 x 2 = 1/8
2. ОДЗ: x >0, обозначим lg x = y
4y 2 + y – 3 = 0, y ≠ 0, y ≠ 1
x 1 = 10 x 2 = 100 4 √1000
Ответ: x 1 = 10 x 2 = 100 4 √1000
x 1 = 0,1 x 2 = 4 √10
Ответ: x Є (0; 0,1) U ( 4 √10; +∞)
б) -1 ≤ y ≤ 0: -y + 1= 1 + y, y = 0
в) y >0: y + 1 = 1 + y, y >0
Ответ: x Є (0; 1/8) U (4; +∞)
Учащимся предлагается выставить оценку за самостоятельную работу.
IV. Домашнее задание :
составить тест по теме «Решение логарифмических уравнений и неравенств». Задания могут быть с выбором ответа или с кратким ответом.
V . Итоги урока. Рефлексия.
- Благодаря сегодняшнему уроку, я …
- Сегодняшний урок помог мне …
- Сегодня на уроке мне запомнилось …
- Сегодня на уроке мне больше всего понравилось …
- После сегодняшнего урока мне захотелось …
- Сегодня на уроке я узнал(а) …
- После сегодняшнего урока я буду знать …
- После сегодняшнего урока я хочу сказать …
- Сегодня на уроке я научился …
- Сегодняшний урок дал мне …
Ребята, вы выставили себе оценки за каждый этап урока. Найдите средний балл, это есть предварительный результат вашей работы на уроке.
Довольны ли вы собой, своей работой?
Поднимите, пожалуйста, руку те, чей средний балл «5» или «4». Это результат хороший.
Ребята, а с теми из вас, кто не доволен результатами своей работы по данной теме, у кого есть вопросы, мы с вами встречаемся на дополнительном занятии.
Благодарю вас за урок и до следующей встречи.
Приложения к уроку
Приложение № 1 – презентация
Приложение № 2 – диагностическая карта
Этапы работы на уроке
1. Решение простейших логарифмических уравнений и неравенств
2. Теоретические сведения о решении логарифмических уравнений и неравенств
4. Работа в группах
5. Самостоятельная работа
Предварительный просмотр:
Подписи к слайдам:
Тема урока: « РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ » « Недостаточно только иметь хороший разум, но главное — это хорошо применять его » Рене Декарт
Логарифмические уравнения Является ли уравнение lg 5+ xlg 6=3 логарифмическим? Существует ли хотя бы одно значение x , при котором верно равенство lg ( x +3)= lgx + lg 3 Записать область определения логарифмического уравнения log a f ( x )= log b g ( x ) в виде системы неравенств. Как решается уравнение, содержащее неизвестное и в основании, и в показателе степени, например x lg x = 10? Нужна ли проверка полученных корней при решении логарифмических уравнений, почему? Решить двумя способами уравнение log 3 ( x +6) + log 3 ( x -2) = 2
Решите уравнения: а) 2 x =3 б) 3 log 3 x =5 в) 7 log 7 x2 =36 г) lg(2x+1)=lgx д) lgx 2 =0 е ) lg(x+1)+lg(x-1)=lg3 ж ) log 2 (x-4)=3 з) log 3 (x+5)=0 и) log 8 (x 2 -1)=1 к ) lg(x-5) =-2 л ) log 3 x=5log 3 2-2log 3 2 м) log 2 (log 3 x)=1 н) log π (log 3 (log 2 x))=0
Логарифмические неравенства Что такое логарифмические неравенства? На чем основано решение логарифмических неравенств? Как решаются логарифмические неравенства вида log g ( x ) f ( x )> b , log g ( x ) f ( x ) log 0.3( x +1) 2 вариант. lg (3 x -7) ≤ lg ( x +1)
первый вариант второй вариант 1.Решить уравнение: log 0.5 (x 2 -4x-1) = -2 log 0.5 (x 2 -3x+10) = -3 1) -1 и 5; 2) 5; 3) 5 и -1; 4) -1. 1) 1; 2) 1 и 2; 3) 2; 4) -1и 2. 2.Укажите промежуток, которому принадлежит корень уравнения: log 2 (7+v) — log 2 (1-v) = 2 log 5 (t+5) – log 5 (t-11) = 1 1) [-7 ; -4]; 2) [-4; -1] 3) [-1 ; 2]; 4) [2 ; 5] 1) (-5; 0); 2) (0; 3); 3) (3; 8); 4) (10; 16) 3. Решить неравенство: log 0.5 (2 x +5) > -3 log 0.5 (2 x -5) 2 1) -1.9; 2) -√5; 3) 2.3; 4) 5 1) √5/2; 2) 2.7; 3) 3; 4) 3.2 Тест
Ответы к тесту Первый вариант 1 3 3 1 Второй вариант 2 4 3 4 Верно 4 задания — оценка «5» 3 задания — оценка «4» 2 задания — оценка «3» Другие варианты — «нужно поработать»
«Для того, чтобы совершенствовать ум, надо больше размышлять, чем заучивать» Р. Декарт
«Скорость нужна, а поспешность вредна» А.В. Суворов Задания в группах: 1) Решить уравнение: x log 6 x /6 = 36 2) Решить неравенство: log 2 3-x (x+0.5)/( x (x-1)) ≤ 0 3) Вычислите абсциссу точки пересечения графиков функций: y = log 0.3 (x 2 — x — 5) и y = log 0.3 (x/3).
Самостоятельная работа I вариант 1.Решить уравнение log 2 0.5 x — log 0.5 x =6 2. Решить неравенство lg 2 x+5lgx+9>0 II вариант 1.Решить уравнение 3/( lgx – 2)+2/( lgx – 3)= -4 2. Решить неравенство lg 2 x 2 + 3lgx > 1 III вариант 1.Решить уравнение |1- log 1/9 x |+1 = |2- log 1/9 x | 2. Решить неравенство log 4 2 x + log 4 √x > 1.5
Проверка самостоятельной работы. I вариант 1. ОДЗ: x >0, обозначим log 0.5 x = y y 2 — y -6=0 y 1 = -2 y 2 = 3 x 1 = 4 x 2 = 1/8 Ответ: x 1 = 4 x 2 = 1/8 2. ОДЗ: x >0, обозначим lg x = y y 2 +5 y +9>0 D 0 Ответ: x >0
Проверка самостоятельной работы. II вариант 1. ОДЗ: x >0, x ≠ 100 , x ≠ 100 0 lg x – 2 = y 3/ y + 2/( y -1) = -4 4 y 2 + y – 3 = 0, y ≠ 0, y ≠ 1 D = 49 y 1 = — 1 y 2 = 3/4 x 1 = 10 x 2 = 100 4√1000 Ответ: x 1 = 10 x 2 = 100 4√1000 2. ОДЗ: x >0 lg x = y 4 y 2 + 3 y – 1 = 0 D = 25 y 1 = -1 y 2 = 1/4 x 1 = 0,1 x 2 = 4√10 Ответ: x Є (0; 0,1) U (4√10; +∞)
Проверка самостоятельной работы. III вариант 1. ОДЗ: x >0 1 – log 1/9 x = y | y |+1 = | 1+ y | а) y 0: y + 1 = 1 + y, y >0 1 – log 1/9 x ≥ 0 log 1/9 x ≤ 1 x ≥ 1/9 Ответ: x ≥ 1/9 2. ОДЗ: x >0 log 4 x = y 2y 2 + y – 3 > 0 D = 25 y 1 = -3/2 y 2 = 1 log 4 x 1 x 4 Ответ : x Є (0; 1/8 ) U ( 4 ; +∞)
«Ошибка одного- урок другому» Д. Рей
Информация о домашнем задании Домашнее задание : составить тест по теме «Решение логарифмических уравнений и неравенств». Задания могут быть с выбором ответа или с кратким ответом .
Рефлексия деятельности Благодаря сегодняшнему уроку, я … Сегодняшний урок помог мне … Сегодня на уроке мне запомнилось … Сегодня на уроке мне больше всего понравилось … После сегодняшнего урока мне захотелось … Сегодня на уроке я узнал(а) … После сегодняшнего урока я буду знать … После сегодняшнего урока я хочу сказать … Сегодня на уроке я научился … Сегодняшний урок дал мне …
По теме: методические разработки, презентации и конспекты
обобщающий урок-игра «Логарифмическая функция, логарифмические уравнения и неравенства».
Методическая разработка+ презентация.
Методическая разработка урока «Логарифмические уравнения»
Методическая разработка урока по алгебре и началам анализа в 10 классе к учебнику Ш.А.Алимова. Первый урок по теме «Логарифмические уравнения». Урок-консультация.
Логарифмы. Логарифмическая функция. Логарифмические уравнения и неравенства.
Обобщающий урок по алгебре и началам анализа в 11 классе на тему :»Логарифмы. Логарифмическая функция. Логарифмические уравнения и неравенства.»Цель урока: — обобщение и систематизация знаний, на.
Логарифмы. Логарифмическая функция. Логарифмические уравнения и неравенства
Урок алгебры и начал математического анализа в 11 А классе по теме « Логарифмы. Логарифмическая функция. Логарифмические уравнения и неравенства».
Методическая разработка уроков: «Логарифмические уравнения и неравенства».
Методическая разработка уроков: «Логарифмические уравнения и неравенства».
Методическая разработка темы Показательные уравнения и неравенства.
Показательные уравнения и неравенства.
разработка урока в 10 классе Решение логарифмических уравнений и неравенств.
обобщающий урок по данной теме, подготовка к контрольной работе.
http://100urokov.ru/predmety/urok-9-uravneniya-logarifmicheskie
http://nsportal.ru/shkola/algebra/library/2013/12/15/metodicheskaya-razrabotka-uroka-reshenie-logarifmicheskikh
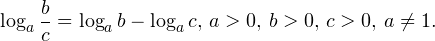 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>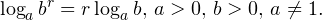 0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>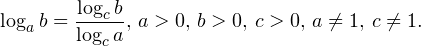 0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>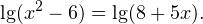
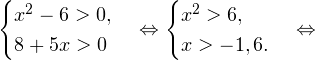 0, \\ 8+5x > 0 \end
0, \\ 8+5x > 0 \end 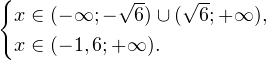
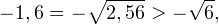 -\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>
-\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>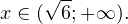
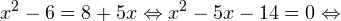
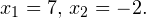
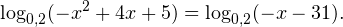
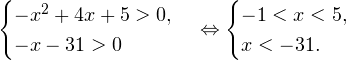 0, \\ -x-31>0 \end
0, \\ -x-31>0 \end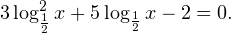
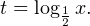
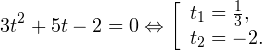
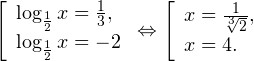
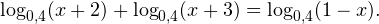
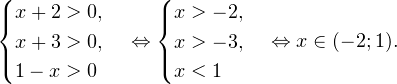 0, \\ x+3>0, \\ 1-x>0 \end
0, \\ x+3>0, \\ 1-x>0 \end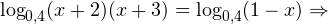
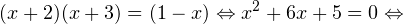
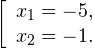
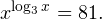
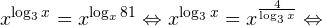
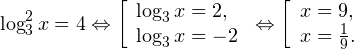
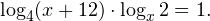
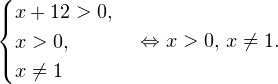 0, \\ x>0, \\ x\ne 1 \end
0, \\ x>0, \\ x\ne 1 \end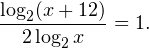
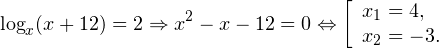
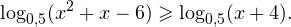
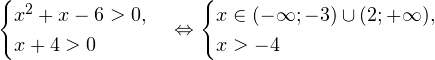 0, \\ x+4>0 \end
0, \\ x+4>0 \end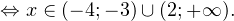
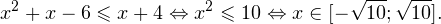
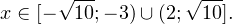
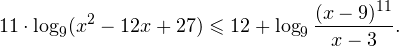
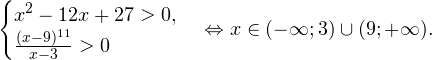 0, \\ \frac<(x-9)^<11>>
0, \\ \frac<(x-9)^<11>>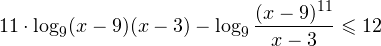
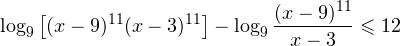
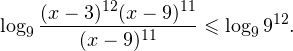
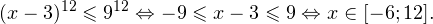
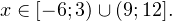
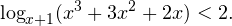
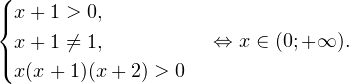 0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end
0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end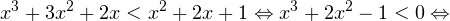
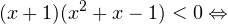
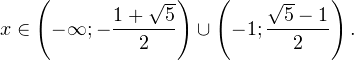
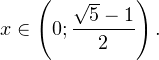
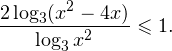
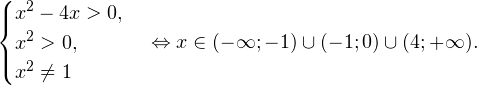 0, \\ x^2>0, \\ x^2\ne 1 \end
0, \\ x^2>0, \\ x^2\ne 1 \end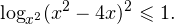
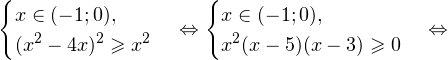
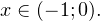
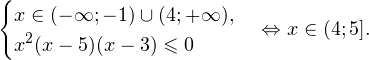
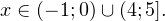
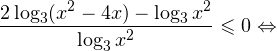
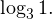 Это ничего не изменит, поскольку
Это ничего не изменит, поскольку 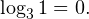
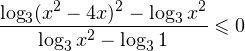
 и
и  — одного знака при
— одного знака при 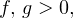 0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход:
0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход: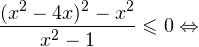
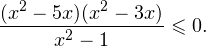
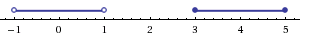
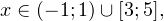 а с учетом области допустимых значений получаем тот же результат:
а с учетом области допустимых значений получаем тот же результат: