12 идеальная жидкость уравнение бернулли сила архимеда

Идеальная жидкость и уравнения, описывающие ее движение

Раздел физики, который изучает особенности движение жидких сред, называется гидродинамикой. Одним из главных математических выражений гидродинамики является уравнение Бернулли для идеальной жидкости. Именно этой теме посвящена статья.

Что такое идеальная жидкость?

Многие знают, что жидкая субстанция представляет собой такое агрегатное состояние материи, которое сохраняет при постоянных внешних условиях объем, но изменяет свою форму при малейшем воздействии на нее. Под идеальной жидкостью понимают такую текучую субстанцию, которая не имеет вязкости и является несжимаемой. Это два главных свойства, которые отличают ее от реальных текучих сред.

Вам будет интересно: Как разобрать предложение по составу? Русский язык

Отметим, что практически все реальные жидкости можно считать несжимаемыми, поскольку для небольшого изменения их объема необходимо огромное внешнее давление. Например, если создать давление в 5 атмосфер (500 кПа), то вода увеличит свою плотность всего на 0,024 %. Что касается вопроса вязкости, то для ряда практических задач, когда в качестве рабочей жидкости рассматривается вода, ею можно пренебречь. Для полноты информации отметим, что динамическая вязкость воды при 20 oC составляет 0,001 Па*с2, что в сравнении с этой величиной для меда (>2000), является мизерным значением.

Важно не путать понятия идеальной жидкости и идеального газа, поскольку последний является легко сжимаемым.

Уравнение непрерывности

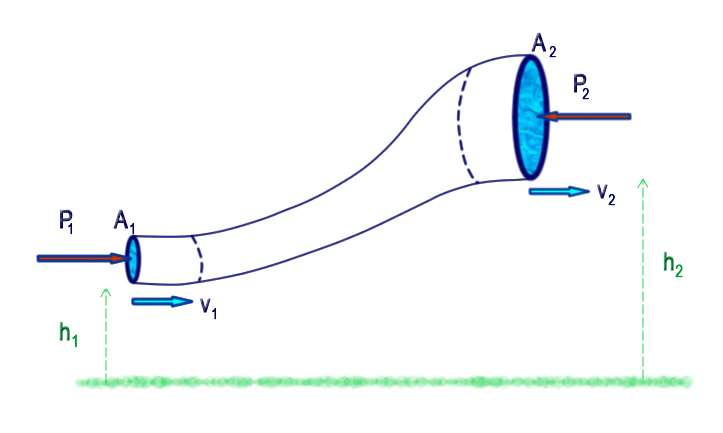
В гидродинамике движение идеальной жидкости начинают рассматривать с изучения уравнения непрерывности ее потока. Чтобы понять суть вопроса, необходимо рассмотреть движение жидкости по трубе. Представим, что на входе труба имеет площадь сечения A1, а на выходе A2.

Теперь предположим, что жидкость течет в начале трубы со скоростью v1, это означает, что за время t через сечение A1 пройдет поток объемом V1 = A1*v1*t. Поскольку жидкость является идеальной, то есть несжимаемой, то точно такой же объем воды должен выйти из конца трубы за время t, получаем: V2 = A2*v2*t. Из равенства объемов V1 и V2 следует уравнение непрерывности потока идеальной жидкости:

Из полученного уравнения следует, что если A1>A2, то v1 должно быть меньше, чем v2. Другими словами, уменьшая сечение трубы, мы тем самым увеличиваем скорость выходящего из нее потока жидкости. Очевидно, что этот эффект наблюдал каждый человек в жизни, кто хотя бы раз поливал из шланга клумбы с цветами или огород, так, прикрывая пальцем отверстие шланга, можно наблюдать, как струя бьющей из него воды становится сильнее.

Уравнение непрерывности для разветвленной трубы

Интересно рассмотреть случай движения идеальной жидкости по трубе, которая имеет не один, а два и более выхода, то есть является разветвленной. Например, площадь сечения трубы на входе равна A1, а к выходу она разветвляется на две трубы с сечениями A2 и A3. Определим скорости потоков v2 и v3, если известно, что на вход вода поступает со скоростью v1.

Используя уравнение непрерывности, получаем выражение: A1*v1 = A2*v2 + A3*v3. Чтобы решить это уравнения относительно неизвестных скоростей, нужно понимать, что на выходе, в какой бы трубе не находился поток, он движется с одинаковой скоростью, то есть v2=v3. Этот факт можно понять интуитивно. Если разделить некоторой перегородкой выходную трубу на две части, скорость потока при этом не изменится. Учитывая этот факт, получаем решение: v2 = v3 = A1*v1/(A2 + A3).

Уравнение Бернулли для идеальной жидкости

Швейцарский физик и математик голландского происхождения Даниил Бернулли в своей работе «Гидродинамика» (1734 год) представил уравнение идеальной жидкости, описывающее ее движение. Оно записывается в следующей форме:

P+ ρ*v2/2 + ρ*g*h = const.

Это выражение отражает закон сохранения энергии в случае течения жидкости. Так, первое слагаемое (P) — давление, направленное вдоль вектора перемещения жидкости, которое описывает работу потока, второе слагаемое (ρ*v2/2) — это кинетическая энергия текучей субстанции, и третье слагаемое (ρ*g*h) — это ее потенциальная энергия.

Напомним, что это уравнение справедливо для идеальной жидкости. В действительности же всегда существует трение текучей субстанции о стенки трубы и внутри ее объема, поэтому в приведенное уравнение Бернулли вводят дополнительный член, описывающий эти энергетические потери.

Использование уравнения Бернулли

Интересно привести некоторые изобретения, в которых используются выводы из уравнения Бернулли:

• Дымоход и вытяжки. Из уравнения следует, что чем больше скорость движения текучей субстанции, тем меньше ее давление. Скорость движения воздуха наверху дымохода больше, чем в его основании, поэтому поток дыма из-за разницы давлений всегда стремится вверх.
• Водопроводные трубы. Уравнение помогает понять, как изменится давление воды в трубе, если изменить диаметр последней.
• Самолеты и «Формула-1». Угол расположения крыльев самолета и антикрыла «Формулы-1» обеспечивает разность давления воздуха над и под крылом, что создает поднимающую и прижимающую силу соответственно.

Режимы течения жидкости

Уравнение Бернулли не учитывает режим движения жидкости, который может быть двух типов: ламинарный и турбулентный. Ламинарный поток характеризуется спокойным течением, при котором слои жидкости движутся по относительно плавным траекториям и не смешиваются между собой. Турбулентный режим движения жидкости характеризуется хаотичным перемещением каждой молекулы, составляющей поток. Особенностью турбулентного режима является наличие завихрений.

Каким способом будет течь жидкость, зависит от ряда факторов (особенности системы, например, наличия или отсутствия шероховатостей на внутренней поверхности трубы, вязкости субстанции и скорости ее перемещения). Переход между рассматриваемыми режимами движения описывается числами Рейнольдса.

Ярким примером ламинарного течения является медленное движение крови по гладким кровеносным сосудам. Пример турбулентного течения — сильный напор воды из крана.

Конспект по физике на тему «Уравнение Бернулли» (10 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Зависимость давления жидкости от скорости ее течения. Движение тел в жидкостях и газах. Уравнение Бернулли. Использование и учет его в технике и жизни .

Один из способов наблюдения течения жидкости состоит в том, что к жидкости подмешивают алюминиевый порошок и следят при сильном освещении за движением алюминиевых блесток. При этом траектории движения этих частиц будут совпадать с линиями тока.

Линии тока – линии, проведенные так, что касательные к ним совпадают по направлению со скоростями частиц жидкости в соответствующих точках пространства.

Свойства линий тока:

1) Цепочки, которые образует алюминиевый порошок, показывают форму линий тока.

2) Через любую точку жидкости можно провести линию тока.

3) Направление линий тока определяется направлением скорости частиц жидкости в данной точке.

4) Густота линий тока характеризует величину скорости в разных точках пространства текущей жидкости: там, где линии тока расположены гуще, скорость больше; там, где линии тока расположены реже, скорость меньше.

Трубка тока – объем жидкости, ограниченный линиями тока.

Скорости элементов жидкости в каждой точке поверхности трубки направлены по касательной к этой поверхности, поэтому частицы при своем движении не пересекают стенок трубки тока.

Различают два вида движения жидкостей:

движение жидкости, при котором отдельные ее слои скользят друг относительно друга, не перемешиваясь.

Движение жидкости, сопровождающееся перемешиванием ее различных слоев с образованием завихрений.

Примеры: течение воды в спокойных реках,

Примеры: поток быстрых рек, океанские течения.

Для описания движения жидкости обычно пользуются следующим методом: фиксируют скорости различных элементов жидкости в одних и тех же точках пространства. Кинематически описать движение реальных жидкостей достаточно сложно. Примем некоторые допущения для упрощения задачи:

1) Ограничимся рассмотрением ламинарного течения.

2) При описании движения жидкости будем рассматривать идеальные жидкости:

Идеальная жидкость – жидкость, вязкостью и сжимаемостью которой можно пренебречь.

Когда мы говорим, что жидкость несжимаема, то имеем в виду, что она не может быть сжата настолько, чтобы заметно изменился ее объем, но очень малое сжатие, вызывающее появление сил упругости, неизбежно происходит.

Вязкость – свойство жидкости оказывать сопротивление относительному перемещению своих частей. Вязкость обусловлена наличием сил внутреннего трения в жидкости.

3) Будем считать, что движение жидкости стационарное:

Скорости элементов жидкости в различных точках пространства, вообще говоря, различны. Если во всех точках пространства скорости элементов жидкости не меняются со временем, то движение жидкости называется стационарным (установившимся).

При стационарном течении любая частица жидкости проходит данную точку с одним и тем же значением скорости. В другой какой-либо точке скорость частицы будет иной, но также постоянной во времени для всех частиц.

Картина линий тока при стационарном течении остается неизменной. Линии тока в этом случае совпадают с траекториями частиц.

Рассмотрим ламинарное течение идеальной жидкости по трубе переменного сечения. Разобьем жидкость на отдельные трубки тока, настолько тонкие, что в каждом сечении скорости элементов жидкости можно считать одинаковыми.

Рассмотрим два сечения S ₁ и S ₂ . Обозначим через и соответствующие скорости течения жидкости.

За малое время Δ t через первое сечение проходит жидкость, масса которой равна: , а через второе — .

Для несжимаемой жидкости и , так как жидкость не пересекает стенок трубки и не может в ней накапливаться. Следовательно:

–уравнение неразрывности несжимаемой жидкости:

модули скоростей несжимаемой жидкости в двух сечениях трубки тока обратно пропорциональны площадям сечений.

Это уравнение справедливо как для стационарного, так и для нестационарного течения.

Давление внутри неподвижной жидкости передается в любую точку этой жидкости без изменений (закон Паскаля). Выясним распределение давления в движущейся жидкости.

Рассмотрим следующий опыт. Возьмем трубку переменного сечения с небольшими отверстиями в стенке, в которые вставлены открытые сверху измерительные трубки. При стационарном течении жидкость в каждой измерительной трубке поднимается до определенной высоты, отсчитываемой от горизонтального уровня. По высоте столба жидкости можно судить о ее давлении на стенки горизонтальной трубки. Опыт показывает, что в широких местах трубки давление больше, чем в узких. Но, согласно уравнению неразрывности несжимаемой жидкости, чем больше сечение трубки, тем меньше скорость течения жидкости. Следовательно, можно сделать вывод:

Закон Бернулли: при стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и наоборот, меньше в тех местах, где больше скорость течения.

Объяснить результат эксперимента можно следующим образом. Так как при переходе жидкости с участка трубы с большей площадью сечения, на участок с меньшей площадью сечения скорость течения увеличивается, то жидкость движется с ускорением, направленным по течению. При переходе жидкости из узкой части в широкую, скорость течения уменьшается, жидкость движется с ускорением, направленным против течения. Согласно II закону Ньютона ускорение вызывается силой и совпадает с ней по направлению. Такой силой может быть лишь равнодействующая сил давления окружающей жидкости на поверхность выделенного объема. Сила давления представляет собой силу упругости сжатой жидкости. Таким образом, в широком участке трубы давление жидкости должно быть больше, чем в узком участке трубы.

Установим зависимость давления идеальной жидкости от скорости ее стационарного течения математически. Пусть труба переменного сечения расположена наклонно к горизонту. Система труба-жидкость-Земля является замкнутой и потенциальной. Воспользуемся теоремой об изменении кинетической энергии.

Согласно теореме об изменении потенциальной энергии:

По определению работы:

(где

— уравнение Бернулли.

где — плотность кинетической энергии или динамическое давление (обусловленное );

— плотность потенциальной энергии или гидростатическое давление (обусловленное гравитационного взаимодействия);

— статическое давление (обусловленное упругого взаимодействия)

Согласно уравнению Бернулли: сумма давления и плотностей кинетической и потенциальной энергий при стационарном течении идеальной жидкости остается постоянной для любого сечения потока.

Если труба горизонтальна, то и уравнение примет вид:

.

Это уравнение показывает, что с увеличением скорости течения давление в жидкости, текущей по горизонтальной трубе, уменьшается .

Применение уравнения Бернулли:

1) Измерение давления и скорости.

Для измерения давления в текущей жидкости используют манометрические трубки, имеющие Г-образную форму с отверстиями. Если располагать трубку, чтобы отверстие было направлено навстречу потоку, скорость жидкости перед отверстием равно нулю; линии тока перед манометром расходятся, не попадая в область перед отверстием. Подставляя в уравнение Бернулли , имеем:

Давление можно измерить с помощью манометрической трубки, помещенной в поток жидкости отверстием вверх (плоскость отверстия расположена параллельно линиям тока). Течение жидкости вдоль боков трубки остается практически таким же как и без трубки, следовательно, показания манометра будут совпадать с показаниями манометра, который движется вместе с жидкостью.

Манометр, обращенный отверстием к потоку, измерит большее давление , чем манометр с отверстием, параллельным линиям тока . Избыток давления получается потому, что частицы жидкости тормозятся перед манометром, вследствие этого давление повышается.

Измерив давление и , можно определить скорость потока:

Эта формула может быть использована для измерения скорости подводной лодки или самолета.

2) Определение скорости истечения жидкостей из отверстия в сосуде.

С помощью уравнения Бернулли можно найти скорость истечения идеальной жидкости из отверстия расположенного в сосуде на глубине h относительно поверхности жидкости. Если сосуд широкий, а отверстие мало, то скорости жидкости в сосуде малы. Ко всему потоку жидкости в целом можно применить уравнение Бернулли. В верхнем сечении у поверхности давление равно атмосферному, а скорость . В нижнем сечении трубки – в отверстии давление также равно атмосферному. Если скорость в отверстии обозначить через , то из уравнения Бернулли для этих двух сечений получим:

Истечение идеальной жидкости происходит с той же скоростью, какую имело бы тело при свободном падении с высоты h .

Применение уравнения Бернулли в технике:

1) Водоструйный насос.

Струя воды подается в трубку А, имеющую на одном конце сужение. По сужению вода течет с большей скоростью. Из-за этого давление в струе в этом месте оказывается меньше атмосферного, воздух из сосуда всасывается в струю через трубку В и удаляется вместе с водой.

Простейший пульверизатор состоит из двух трубок, расположенных перпендикулярно друг другу. Через горизонтальную трубку продувается воздух. В узкой части струи при выходе из трубки давление меньше атмосферного. Атмосферное давление поднимает жидкость по вертикальной трубке, и она распыляется струей воздуха.

3) Карбюратор – прибор, предназначенный для питания двигателя внутреннего сгорания горючей смесью.

Во время всасывающих тактов движения поршня двигателя наружный воздух проходит по трубе, которая имеет суженную часть – диффузор. В диффузоре помещен жиклер (распылитель воздуха) – трубка с малым отверстием. Жиклер соединен с поплавковой камерой карбюратора. При прохождении потока воздуха его скорость в диффузоре резко возрастает, давление становится меньше атмосферного и атмосферное давление выталкивает бензин из поплавковой камеры через жиклер. Бензин распыляется в потоке воздуха – образуется рабочая смесь, которая поступает в цилиндр двигателя.

Жидкости и газы существенно отличаются друг от друга. Различие между жидкостями и газами обусловлено большой сжимаемостью газов. Несмотря на это, явления в неподвижных жидкостях и газах аналогичны (закон Паскаля, закон Архимеда). При исследовании движения в жидкостях и газах эта аналогия во многом сохраняется, а именно: при движении газов со скоростями, значительно меньшими скорости звука (340м/с), сжимаемость газов достаточно мала и ее можно не учитывать. В связи с этим полученные ранее законы и утверждения можно применять и для газов.

Применим уравнение Бернулли для расчета подъемной силы крыла самолета.

При отсутствии сил сопротивления воздуха крыло обтекает ламинарный поток. Согласно уравнению Бернулли:

и

Если учитывать сопротивление воздуха, картина будет другая. Когда воздушный поток начинает обтекать крыло, то из-за действия сил трения у задней кромки образуется вихрь, в котором воздух вращается против часовой стрелки, если крыло движется влево. Применим уравнение Бернулли:

(т.к. вблизи точки 2 образуется вихрь) и .

Но по закону сохранения момента импульса при возникновении вращения против часовой стрелки должно возникнуть вращение по часовой стрелке.

Такое вращение воздуха и возникает вокруг крыла. На обтекающий крыло поток накладывается циркуляция воздуха вокруг крыла. В результате скорость воздушного потока над крылом оказывается больше, чем под крылом, так как над крылом скорость циркуляции имеет такое же направление, как и скорость набегающего на крыло потока, а под крылом эти скорости противоположны по направлению. Но согласно закону Бернулли давление должно быть больше там, где скорость меньше. Следовательно, под крылом самолета давление больше, чем над ним. Из-за этого и возникает подъемная сила.

и .

Известно, что наименьшая сила сопротивления действует на тело каплеобразной формы. Такая форма крыла самолета обеспечивает хорошую его обтекаемость.

Элементы механики жидкостей и газов

Элементы механики жидкостей и газов

1. Давление. Закон Паскаля. Гидростатическое давление. Сила Архимеда.

2. Уравнение неразрывности.

3. Уравнение Бернулли.

4. Вязкость (внутренне трение).

5. Число Рейнольдса. Принцип подобия.

6. Методы определения вязкости: метод Стокса; формула Пуазейля.

1. Давление – это сила, действующая на единицу площади:

, или, точнее: . (6.1)

Размерность давления .

По закону Паскаля давление в любой точке покоящегося газа или жидкости одинаково по всем направлениям и одинаково передаётся по всему объёму.

Гидростатическое давление жидкости на глубине h под свободной поверхностью жидкости, обусловленное её весом, равно:

. (6.2)

Закон Архимеда : на тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу вытесненной телом жидкости (газа):

, (6.3)

где – объём погружённой в жидкость части тела. Действие силы Архимеда обусловлено разностью гидростатического давления на разной глубине.

Далее будем рассматривать движущуюся жидкость (газ).

Гидроаэромеханика – это раздел механики , в котором изучаются законы равновесия и движения жидкой (и газообразной) среды и её взаимодействия с телами, обтекаемыми этой средой. Плотность жидкости практически не зависит от давления, поэтому жидкость в гидродинамике считаем несжимаемой. Для газа, вообще говоря, это не так, но опыт показывает, что при не слишком больших скоростях потока сжимаемостью газа можно пренебречь. Гидроаэромеханика использует единый подход для описания поведения жидкостей и газов.

В гидроаэродинамике отвлекаются от молекулярного строения жидкости и рассматривают её как сплошную, непрерывную среду. Частицей среды будем называть малый элемент объёма среды, размеры которого много больше межмолекулярных расстояний, но в то же время столь малы, что в пределах её параметры потока (давление, скорость течения) можно считать одинаковыми.

Для описания течения жидкости задают поле скоростей частиц жидкости, то есть зависимость скоростей частиц от координат (радиус-вектора) и времени: . В случае установившегося (стационарного) течения скорость потока в данной точке от времени не зависит.

Линией тока называется мысленно проведённая линия, касательная к которой в каждой точке совпадает с направлением скорости частиц .

Трубка тока – это поверхность, образованная линиями тока, проведёнными через все точки замкнутого контура. При установившемся течении линии тока не изменяются, и частицы жидкости не пересекают поверхность трубки тока, так как линия тока – это, по существу, траектория частицы.

2. Уравнение неразрывности.

Рассмотрим стационарное течение несжимаемой жидкости. Возьмём трубку тока, ограниченную перпендикулярными к направлению скорости сечениями S 1 и S 2 (рис.6.1), достаточно малыми, чтобы в пределах сечения скорость частиц жидкости можно было считать постоянной: в сечении S1 скорость равна , в сечении S 2 – . Поскольку жидкость несжимаема (ρ= const ), то объём жидкости, поступающий через первое сечение, равен объёму жидкости, вытекающей через второе сечение за тот же промежуток времени :

, (6.4)

, (6.5)

где и – путь, пройденный частицами жидкости в соответствующем сечении за время . Тогда получим:

,

. (6.6)

Соотношение (6.6) – это уравнение неразрывности струи.

Объёмным расходом жидкости называется объём, протекающий через сечение за единицу времени:

. (6.7)

.

Если сечения трубки тока нельзя считать малыми, то для вычисления объёмного расхода нужно интегрировать по сечению трубки тока:

.

Уравнение неразрывности, по существу, означает равенство объёмного расхода в любом сечении трубки тока, если течение стационарно.

Массовым расходом называется масса жидкости, протекающая через сечение за единицу времени:

, (6.8)

.

В реальных жидкостях между отдельными слоями потока есть внутренне трение (вязкость). Но в ряде случаев влиянием вязкости жидкости можно пренебречь (вязкость воды и спирта, например, в обычных условиях очень невелика), а вязкость газа вообще очень незначительна.

Идеальной жидкостью называется жидкость без внутреннего трения (без вязкости).

Рассмотрим стационарно текущую идеальную жидкость (рис.6.2). Сечения опять будем считать достаточно малыми, так что скорости частиц жидкости в пределах сечения одинаковы, а кроме того, размеры сечения много меньше его высоты h над выбранным уровнем. За время dt жидкость, находящаяся между сечениями, проходящими через точки А и В, заполнит участок между точками A ` и B `.

Поскольку течение стационарно, состояние жидкости между сечениями, проходящими через точки A ` и B , не изменяется, так что этот участок можно не рассматривать и считать, что масса жидкости () за время dt переместилась из положения АА` с высоты h 1 в положение ВВ` на высоту h 2 . Внутреннего трения нет, поэтому работа внешних сил давления идёт только на увеличение механической энергии массы жидкости dm :

. (6.9)

Работа силы давления в сечении S 1 при перемещении на dl 1 :

, (6.10)

так как сила давления , а объём протекшей жидкости . Аналогично работа в сечении S2 при перемещении на dl 2 :

. (6.11)

Знак «минус» указывает на то, что в этом сечении направления силы давления и перемещения противоположны. Работа сил давления, действующих на боковую поверхность цилиндра, равна нулю, так как эти силы перпендикулярны поверхности, а следовательно, и перемещению частиц жидкости.

Далее, начальная механическая энергия массы dm , движущейся со скоростью v 1 и находящейся на высоте h 1 , равна

. (6.12)

Механическая энергия через dt на высоте h 2 аналогично:

, (6.13)

Плотность равна , поэтому

,

. (6.14)

Это – уравнение Бернулли.

Его можно записать так:

, (6.14а)

то есть сумма статического давления p, динамического и гидростатического в любом сечении трубки тока остаётся постоянной. Отсюда, в частности, следует, что в горизонтальной трубе в местах сужения, где скорость потока больше, статическое давление падает.

4. Вязкость (внутренне трение).

Во всех реальных жидкостях и газах при перемещении одного слоя относительно другого возникают силы трения. Со стороны слоя, движущегося более быстро, на слой, движущийся медленнее, действует ускоряющая сила. Наоборот, со стороны слоя, движущегося медленнее, на более быстрый слой действует тормозящая сила. Эти силы, носящие название сил внутреннего трения, направлены по касательной к поверхности слоёв.

Пусть два слоя (рис.6.3) площади , отстоящих друг от друга на расстояние , движутся со скоростями v 1 и v 2 соответственно, Δ v = v 2 – v 1 . Направление, в котором отсчитывается расстояние между слоями (ось z ), перпендикулярно вектору скорости движения слоев. Величина

,

которая показывает, как быстро меняется скорость при переходе от слоя к слою, называется градиентом скорости. Величина силы внутреннего трения , действующей между слоями, пропорциональна площади соприкосновения движущихся слоёв и градиенту скорости (закон Ньютона):

, (6.15)

где – коэффициент вязкости (динамическая вязкость). Знак «–» показывает, что сила направлена противоположно градиенту скорости, то есть быстрый слой тормозится, а медленный – ускоряется.

Единицей измерения коэффициента вязкости в СИ служит такая вязкость, при которой градиент скорости, равный 1 м/с на 1м, приводит к силе внутреннего трения в 1 Н на 1 м2 площади слоев. Эта единица называется паскаль-секундой (Па. с). В некоторые формулы (например, число Рейнольдса, формула Пуазейля) входит отношение коэффициента вязкости к плотности жидкости ρ. Это отношение получило название коэффициента кинематической вязкости :

. (6.16)

Для жидкостей, течение которых подчиняется уравнению Ньютона (6.16), вязкость не зависит от градиента скорости. Такие жидкости называются ньютоновскими. К неньютоновским (то есть не подчиняющимся уравнению (6.16)) жидкостям относятся жидкости, состоящие из сложных и крупных молекул, например, растворы полимеров.

Вязкость данной жидкости сильно зависит от температуры: при изменениях температуры, которые сравнительно нетрудно осуществить на опыте, вязкость некоторых жидкостей может изменяться в миллионы раз. При понижении температуры вязкость некоторых жидкостей настолько возрастает, что жидкость теряет текучесть, превращаясь в аморфное твердое тело.

вывел формулу, связывающую коэффициент вязкости жидкости с температурой:

, (6.17)

где А – множитель, который зависит от расстояния между соседними положениями равновесия молекул в жидкости и от частоты колебаний молекул, ΔЕ – энергия, которую надо сообщить молекуле жидкости, чтобы она могла перескочить из одного положения равновесия в другое, соседнее (энергия активации). Величина ΔЕ обычно имеет порядок (2÷3).10-20 Дж, поэтому, согласно формуле (16.3), при нагревании жидкости на 100С вязкость её уменьшается на 20÷30%.

Значения коэффициентов вязкости газов существенно меньше, чем жидкостей. С повышением температуры вязкость газа увеличивается (рис.6.4) и при критической температуре становится равной вязкости жидкости.

Отличие в характере поведения вязкости при изменении температуры указывает на различие механизма внутреннего трения в жидкостях и газах. Молекулярно-кинетическая теория объясняет вязкость газов переносом импульса из одного слоя в другой слой, происходящим за счет переноса вещества при хаотическом движении молекул газа. В результате в слое газа, движущемся медленно, увеличивается доля быстрых молекул, и его скорость (средняя скорость направленного движения молекул) возрастает. Слой газа, движущийся медленно, увлекается более быстрым слоем, а слой газа, движущийся с большей скоростью, замедляется. С повышением температуры интенсивность хаотического движения молекул газа возрастает, и вязкость газа увеличивается.

Вязкость жидкости имеет другую природу. В силу малой подвижности молекул жидкости перенос импульса из слоя в слой происходит из-за взаимодействия молекул. Вязкость жидкости в основном определяется силами взаимодействия молекул между собой (силами сцепления). С повышением температуры взаимодействие молекул жидкости уменьшается, и вязкость также уменьшается.

Несмотря на различную природу вязкость жидкостей и газов с макроскопической точки зрения описывается одинаковым уравнением (6.15). Величину импульса , перенесенного из одного слоя газа или жидкости в другой слой за время Δ t , можно найти из второго закона Ньютона:

. (6.18)

Из (16.1) и (16.4) получим:

. (6.19)

Тогда физический смысл коэффициента динамической вязкости можно сформулировать так: коэффициент вязкости численно равен импульсу, перенесенному между слоями жидкости или газа единичной площади за единицу времени при единичном градиенте скорости. Знак «минус» показывает, что импульс переносится из более быстрого слоя в более медленный.

5. Число Рейнольдса. Принцип подобия.

Различают два режима течения: ламинарное (слоистое) – без перемешивания слоёв (рис.6.5) и турбулентное (вихревое) – с перемешиванием, то есть в отдельных точках потока скорости отдельных частиц перпендикулярны потоку (рис.6.6).

На рис.6.7 видно, как с увеличением скорости обтекания тела ламинарное течение становится неустойчивым, хаотичным и переходит в турбулентное.

Для того, чтобы оценить характер течения жидкости, вводится безразмерная величина , называемая числом Рейнольдса.

(6.20)

Здесь – средняя скорость потока, – кинематическая вязкость, – характерный размер (в случае течения жидкости в трубе это диаметр трубы ). Опытные данные показывают, что существует критическое число Рейнольдса, при превышении которого происходит переход из ламинарного режима в турбулентный. Но сама величина не универсальна – она зависит от геометрии системы. Для случая течения жидкости в трубе .

Число Рейнольдса имеет огромное значение при моделировании реальных процессов в лабораторных масштабах. Если для двух течений разных размеров числа Рейнольдса одинаковы, то такие течения подобны, и возникающие в них явления могут быть получены одно из другого изменением масштаба.

6. Методы определения вязкости.

При движении тела в вязкой среде возникают силы сопротивления. Происхождение этого сопротивления двояко.

При небольших скоростях , когда за телом нет вихрей (то есть обтекание тела ламинарное), сила сопротивления обуславливается вязкостью среды. Между движущимся телом и средой существуют силы сцепления, так что непосредственно вблизи поверхности тела слой газа (жидкости) полностью задерживается, как бы прилипая к телу. Он трется о следующий слой, который слегка отстает от тела. Тот, в свою очередь, испытывает силу трения со стороны еще более удаленного слоя и т. д. Совсем далекие от тела слои можно считать покоящимися. Для ламинарного потока сила трения пропорциональна скорости тела: . Теоретический расчет внутреннего трения для движения шарика в вязкой среде с небольшой скоростью, когда нет вихрей, приводит к формуле Стокса:

, (6.21)

где – радиус шарика, – скорость его движения, – коэффициент динамической вязкости среды.

Второй механизм сил сопротивления включается при больших скоростях движения тела, когда поток становится турбулентным. При увеличении скорости тела вокруг него возникают вихри. Часть работы, совершаемой при движении тела в жидкости или газе, идет на образование вихрей, энергия которых переходит во внутреннюю энергию. При турбулентном потоке в некотором интервале скоростей сила сопротивления пропорциональна квадрату скорости тела: .

Метод Стокса основан на измерении скорости установившегося движения твердого шарика в вязкой среде под действием постоянной внешней силы, в простейшем случае – силы тяжести.

Выведем рабочую формулу для определения коэффициента вязкости методом Стокса. Если взять шарик большей плотности, чем плотность жидкости, то он будет тонуть, опускаясь на дно сосуда. На падающий шарик действуют три силы (рис.6.8):

1. сила вязкого трения FС по закону Стокса (16.6), направленная вверх, навстречу скорости: ;

2. сила тяжести, направленная вниз:

, (6.22)

где – масса шарика; – плотность шарика; – ускорение свободного падения; – объем шарика, равный:

; (6.23)

3. выталкивающая сила FАрх, согласно закону Архимеда, равная весу вытесненной жидкости:

, (6.24)

где – плотность жидкости.

Запишем уравнение движения (второй закон Ньютона) для падающего шарика в проекциях на вертикальную ось:

Сила тяжести и выталкивающая сила не зависят от скорости движения шарика. Сила трения в законе Стокса прямо пропорциональна скорости. Поэтому на некотором начальном участке l 0 (рис.6.8) падения шарика в жидкости, пока скорость мала, сила трения меньше разности сил тяжести и выталкивающей, и шарик в результате движется с ускорением. Величину участка можно оценить из уравнения движения.

По мере нарастания скорости падения шарика растет сила вязкого трения. С момента достижения равенства

сумма сил, действующих на шарик, становится равной нулю, и шарик, в соответствии с первым законом Ньютона, движется по инерции равномерно, с набранной им к этому моменту скоростью. По измеренной скорости установившегося падения шарика можно найти коэффициент вязкости жидкости η .

После подстановки в (6.26) выражений (6.22-6.24) получим:

.

Сократим на радиус и сделаем замену ( – диаметр шарика):

;

. (6.27)

Из (6.27) выразим коэффициент динамической вязкости:

. (6.28)

Далее скорость v шарика выражаем через пройденный путь и время падения : :

. (6.29)

Выведенная формула (6.29) для расчета коэффициента вязкости, как и формула Стокса (6.21), получены в предположении, что шарик движется в сосуде неограниченного объема.

б) формула Пуазейля

Ламинарный параллельный поток имеет место, например, при медленном протекании газа в цилиндрической трубе (капилляре) – в этом случае слои представляют собой совокупность бесконечно тонких цилиндрических поверхностей, вложенных одна в другую, имеющих общую ось, совпадающую с осью трубы.

Выделим в капилляре воображаемый цилиндрический объем жидкости (или газа) радиусом и длиной , как показано на рисунке 6.9. Обозначим давления на его торцах и . При установившемся течении суммарная сила давления на цилиндр

уравновесится силой внутреннего трения , которая действует на боковую поверхность цилиндра со стороны внешних слоев газа:

. (6.30)

Сила внутреннего трения определяется по формуле Ньютона (6.15). Учитывая, что (площадь поверхности цилиндра) и скорость уменьшается при удалении от оси трубы, т. е., можно записать:

(6.31)

В этом случае условие стационарности (5.30) запишется в виде:

(6.32)

Интегрируя это равенство, получим

,

где – постоянная интегрирования, которая определяется граничными условиями задачи. При скорость жидкости должна обратиться в нуль:, поскольку сила внутреннего трения о стенку капилляра тормозит смежный с ней слой жидкости. Тогда

. (6.33)

Рис.6.5 иллюстрирует получившуюся квадратичную (параболическую) зависимость скорости частиц жидкости от расстояния до оси капилляра при ламинарном течении.

Подсчитаем объемный расход жидкости , т. е. объем, который протекает за единицу времени через поперечное сечение трубы. Через кольцевую площадку с внутренним радиусом и внешним за время протекает объем жидкости, равный произведению площади этой кольцевой площадки на перемещение частиц жидкости за это время :

;

.

;

,

. (6.34)

Формулу (6.34) называется формулой Пуазейля. Она позволяет экспериментально определить динамическую вязкость жидкости (газа), измерив объёмный расход и зная разность давлений на концах капилляра и его геометрические параметры.