Информационно — реферативная работа по математике «13 способов решения квадратных уравнений», 8 класс
анотация на информационно — реферативную работу по математике
«13 способов решения квадратных уравнений»
Тема работы весьма актуальна в настоящее время. Работа отвечает выбранной теме, расширяет рамки программы общеобразовательной школы.
Информационно — реферативная работа структурно выстроена правильно, логична, чётко сформулированы цель и задачи, имеются исследования и выводы по работе.
Работа грамотно изложена, прослеживается логическая связь между частями работы, отличается завершённостью.
В работе учащиеся проявили исследовательские качества, самостоятельность в изучении большого объёма специализированной литературы, компьютерную грамотность в оформлении и создании презентации к защите.
Содержание отвечает выбранной теме, которая полностью раскрыта.
Скачать:
| Вложение | Размер |
|---|---|
| Информационно — реферативная работа по математике «13 способов решения квадратных уравнений» | 512 КБ |
Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 6
городского поселения «Рабочий посёлок Чегдомын»
Верхнебуреинского муниципального района
Информационно — реферативная работа по математике
«13 способов решения квадратных уравнений»
- Введение………………………………………………………стр 3
- Понятие квадратного уравнения…………………………… стр 4
- Виды квадратных уравнений……………………………..….стр 5
- Исторические сведения…………………………….……..…..стр.7
- Способы решения квадратных уравнений………………… стр.8
- Заключение…………………………………………………. стр.18
В восьмом классе мы изучили квадратные уравнения и некоторые способы их решения. Нам стало интересно, существуют ли другие способы решения этих уравнений.
Объектом нашего исследования являются квадратные уравнения.
Целью работы является: изучение различных способов решения квадратных уравнений.
Актуальность нашей темы в том, что умело выбирая способы решения квадратных уравнений, мы экономим время на выполнение самостоятельных и контрольных работ, а так же на экзамене.
- изучить виды квадратных уравнений
- освоить наиболее доступные и распространенные способы решения
Уравнения вида (1), где — действительные числа, причем , х – переменная, называют квадратным уравнением. Если а = 1, то квадратное уравнение называют приведенным. Числа носят следующие названия: а — коэффициент первый, в — второй коэффициент, с – свободный член.
Корни уравнения находят по формуле
Выражение называют дискриминантом квадратного уравнения (1)
- Если D ‹ 0 , то уравнение (1) не имеет действительных корней;
- Если , то уравнение (1) имеет один действительный корень;
- Если , то уравнение (1) имеет два действительных корня.
В случае, когда , иногда говорят, что квадратное уравнение имеет два одинаковых корня.
Используя обозначение , можно переписать формулу (2) в виде
Если , то формула (2) принимает вид:
Формула (3) особенно удобна в тех случаях, когда — целое число, т.е. коэффициент – четное число.
Пример . Решить уравнение .
Здесь = 2, = -5, = 2. Находим = . Так как , то уравнение имеет два корня, которые мы найдем по формуле(2): ;
Итак, ; , т.е. х 1 =2, х 2 = ½ — корни заданного уравнения. Ответ: 2, ½
Пример . Решить уравнение х 2 – 6х + 9 = 0. Здесь а = 1, в = -6, с = 9. Т.к. в = 6 – четное число, то воспользуемся формулой (3). Находим , т.е. х = 3 – корень уравнения. Ответ: х = 3
Пример . Решить уравнение 2х 2 – 5х + 2 = 0
Здесь а = 2, в = -3, с = 5. Находим D = в 2 – 4ас = (-3) 2 – 4*2*5 = 9 — 40 = — 31. Так как D 0 то уравнение не имеет действительных корней.
2. Неполные квадратные уравнения
История появления решений квадратных уравнений
Квадратные уравнения в Древнем Вавилоне.
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных Если в квадратном уравнении ах 2 + bх + с = 0 второй коэффициент в или свободный член с равен нулю, то квадратное уравнение называют неполным. Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения – проще решить его методом разложения его левой части на множители. Пример . Решить уравнение 2х 2 – 6х = 0
Имеем 2х(х – 3) = 0. Значит, либо х = 0, либо х – 3 = 0, т.е. х = 3. Уравнение имеет два корня х = 0, х = 3.
Ответ: х = 0, х = 3.
, и такие, например, полные квадратные уравнения:
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Как составил и решил Диофант квадратные уравнения.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача: «Найти два числа, зная, что их сумма равна 20, а произведение — 96».
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х, другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение: (10+x)(10—x) =96,
или же100 —x 2 = 96.
Отсюда х =± 2. Одно из искомых чисел равно 12, другое 8. Решение х = — 2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравненияy(20-y)=96
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.
Квадратные уравнения в Индии.
Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:ax 2 + bх = с, а> 0. (1)
В уравнении (1) коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
«Обезьянок резвых стая
А двенадцать по лианам
Всласть поевши, развлекалась
Стали прыгать, повисая
Их в квадрате часть восьмая
Сколько ж было обезьянок,
На поляне забавлялась
Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений.Соответствующее задаче уравнение
Бхаскара пишет: x 2 — 64x = — 768и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:
x 2 — б4х + 32 2 = -768 + 1024,
x 1 = 16, x 2 = 48.
Квадратные уравнения у ал-Хорезми.
В алгебраическом трактате ал-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1. «Квадраты равны корням», т. е. ах 2 = bх.
2.«Квадраты равны числу», т. е. ах 2 = с.
- «Корни равны числу», т. е. ах = с.
- «Квадраты и числа равны корням», т. е. ах 2 + с = bх.
- «Квадраты и корни равны числу», т. е. ах 2 + bх =с.
- «Корни и числа равны квадратам», т. е. bх + с == ах 2 .
Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Задача: «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х 2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат ал-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
4. Способы решения квадратных уравнений
Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений.
1. СПОСОБ : Разложение левой части уравнения на множители.
Решим уравнение х 2 + 10х — 24 = 0 .
Разложим левую часть на множители:
х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2 , а также при х = — 12 . Это означает, что число 2 и — 12 являются корнями уравнения х 2 + 10х — 24 = 0 .
2. СПОСОБ : Метод выделения полного квадрата.
Решим уравнение х 2 + 6х — 7 = 0 .
Выделим в левой части полный квадрат.
Для этого запишем выражение х 2 + 6х в следующем виде:
х 2 + 6х = х 2 + 2• х • 3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 3 2 , так какх 2 + 2• х • 3 + 3 2 = (х + 3) 2 . Преобразуем теперь левую часть уравнения х 2 + 6х — 7 = 0 ,прибавляя к ней и вычитая 3 2 . Имеем:
х 2 + 6х — 7 = х 2 + 2• х • 3 + 3 2 — 3 2 — 7 = (х + 3) 2 — 9 — 7 = (х + 3) 2 — 16.
Таким образом, данное уравнение можно записать так:
(х + 3) 2 — 16 =0, (х + 3) 2 = 16.
Следовательно, х + 3 — 4 = 0, х 1 = 1, или х + 3 = -4, х 2 = -7.
3. СПОСОБ : Решение квадратных уравнений по формуле.
Умножим обе части уравнения ах 2 + bх + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а 2 х 2 + 4аbх + 4ас = 0,
((2ах) 2 + 2ах • b + b 2 ) — b 2 + 4ac = 0,
(2ax + b) 2 = b 2 — 4ac,
2ax + b = ± √ b 2 — 4ac,
2ax = — b ± √ b 2 — 4ac,
а) Решим уравнение: 4х 2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b 2 — 4ac = 7 2 — 4 • 4 • 3 = 49 — 48 = 1,
D> 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b 2 — 4ac>0 , уравнение ах 2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х 2 — 4х + 1 = 0,
а = 4, b = — 4, с = 1, D = b 2 — 4ac = (-4) 2 — 4 • 4 • 1= 16 — 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b 2 — 4ac = 0 , то уравнение
ах 2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х 2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b 2 — 4ac = 3 2 — 4 • 2 • 4 = 9 — 32 = — 13 , D
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b 2 — 4ac ,
уравнение ах 2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах 2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х 2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x 1 x 2 = q,
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен ( q> 0 ), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p . Если р , то оба корня отрицательны, если р , то оба корня положительны.
x 2 – 3x + 2 = 0; x 1 = 2 и x 2 = 1, так как q = 2 > 0 и p = — 3
x 2 + 8x + 7 = 0; x 1 = — 7 и x 2 = — 1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен ( q ), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p> 0 .
x 2 + 4x – 5 = 0; x 1 = — 5 и x 2 = 1, так как q= — 5 и p = 4 > 0;
x 2 – 8x – 9 = 0; x 1 = 9 и x 2 = — 1, так как q = — 9 и p = — 8
5. СПОСОБ: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение ах 2 + bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + аbх + ас = 0.
Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению
равносильно данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.
Окончательно получаем х 1 = у 1 /а и х 1 = у 2 /а .
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Решим уравнение 2х 2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение у 2 – 11у + 30 = 0.
Согласно теореме Виета
у 1 = 5 х 1 = 5/2 x 1 = 2,5
у 2 = 6 x 2 = 6/2 x 2 = 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение ах 2 + bх + с = 0, где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х 1 = 1,
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение x 2 + b/a • x + c/a = 0.
Согласно теореме Виета
По условию а – b + с = 0, откуда b = а + с. Таким образом,
x 1 + x 2 = — а + b/a= -1 – c/a,
x 1 x 2 = — 1• ( — c/a),
т.е. х 1 = -1 и х 2 = c/a , что м требовалось доказать.
- Решим уравнение 345х 2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
х 1 = 1, х 2 = c/a = -208/345.
2)Решим уравнение 132х 2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
х 1 = 1, х 2 = c/a = 115/132.
Б. Если второй коэффициент b = 2k – четное число, то формулу корней
Решим уравнение 3х2 — 14х + 16 = 0 .
Решение . Имеем: а = 3, b = — 14, с = 16, k = — 7 ;
D = k 2 – ac = (- 7) 2 – 3 • 16 = 49 – 48 = 1, D> 0, два различных корня;
В. Приведенное уравнение
совпадает с уравнением общего вида, в котором а = 1 , b = р и с = q . Поэтому для приведенного квадратного уравнения формула корней
Формулу (3) особенно удобно использовать, когда р — четное число.
Пример. Решим уравнение х 2 – 14х – 15 = 0.
Решение. Имеем: х 1,2 =7±
Ответ: х 1 = 15; х 2 = -1.
7. СПОСОБ: Графическое решение квадратного уравнения.
Если в уравнении х 2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
Построим графики зависимости у = х 2 и у = — px — q.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости — прямая (рис.1). Возможны следующие случаи:
— прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
— прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
1) Решим графически уравнение х 2 — 3х — 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х 2 = 3х + 4 .
Построим параболу у = х 2 и прямую у = 3х + 4 . Прямую
у = 3х + 4 можно построить по двум точкам М (0; 4) и
N (3; 13) . Прямая и парабола пересекаются в двух точках
А и В с абсциссами х 1 = — 1 и х 2 = 4 . Ответ : х 1 = — 1; х 2 = 4.
2) Решим графически уравнение (рис. 3) х 2 — 2х + 1 = 0 .
Решение. Запишем уравнение в виде х 2 = 2х — 1 .
Построим параболу у = х 2 и прямую у = 2х — 1.
Прямую у = 2х — 1 построим по двум точкам М (0; — 1)
и N(1/2; 0) . Прямая и парабола пересекаются в точке А с
абсциссой х = 1 . Ответ: х = 1.
3) Решим графически уравнение х 2 — 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х 2 = 5х — 5 . Построим параболу у = х 2 и прямую у = 2х — 5 . Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х 2 — 2х + 5 = 0 корней не имеет.
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки.
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + bх + с = 0 с помощью циркуля и линейки (рис. 5).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х 1 ; 0 ) и D (х 2 ; 0), где х 1 и х 2 — корни уравнения ах 2 + bх + с = 0 , и проходит через точки
А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC , откуда OC = OB • OD / OA= х 1 х 2 / 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK , восстановленных в серединах хорд AC и BD , поэтому
1) построим точки (центр окружности) и A(0; 1) ;
2) проведем окружность с радиусом SA ;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS>SK, или R>a + c/2a) , окружность пересекает ось Ох в двух точках (рис. 6,а) В(х 1 ; 0) и D(х 2 ; 0) , где х 1 и х 2 — корни квадратного уравнения ах 2 + bх + с = 0 .
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a) , окружность касается оси Ох (рис. 6,б) в точке В(х 1 ; 0) , где х 1 — корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
Решим уравнение х 2 — 2х — 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1).
Ответ:х 1 = — 1; х 2 = 3.
9. СПОСОБ: Решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни
z 1 = 8,0 и z 2 = 1,0 (рис.12).
2) Решим с помощью номограммыуравнение 2z 2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z 2 — 4,5z + 1 = 0. Номограмма дает корни z 1 = 4 и z 2 = 0,5.
3) Для уравнения z 2 — 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t , получим уравнение t 2 — 5t + 2,64 = 0, которое решаем посредством номограммы и получим t 1 = 0,6 и t 2 = 4,4, откуда z 1 = 5t 1 = 3,0 и z 2 = 5t 2 = 22,0.
10. СПОСОБ: Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
1) Решим уравнение х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25) , т.е. S =х 2 + 10х + 25. Заменяя
х 2 + 10х числом 39 , получим, что S = 39 + 25 = 64 , откуда следует, что сторона квадрата ABCD , т.е. отрезок АВ = 8 . Для искомой стороны х первоначального квадрата получим
2) А вот, например, как древние греки решали уравнение у 2 + 6у — 16 = 0 .
Решение представлено на рис. 16, где у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9. Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у 2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у 1 = 2, у 2 = — 8 (рис.16).
3) Решить геометрически уравнение у 2 — 6у — 16 = 0.
Преобразуя уравнение, получаем у 2 — 6у = 16.
На рис. 17 находим «изображения» выражения у 2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3 . Значит, если к выражению у 2 — 6у прибавить 9 , то получим площадь квадрата со стороной у — 3 . Заменяя выражение у 2 — 6у равным ему числом 16,
получаем: (у — 3) 2 = 16 + 9, т.е. у — 3 = ± √25 , или у — 3 = ± 5, где у 1 = 8 и
Журнал Педагог
Автор: Савельева Ольга Николаевна
Должность: учитель математики
Учебное заведение: МАОУ «СОШ № 30»
Населённый пункт: город Стерлитамак, Республики Башкортостан
Наименование материала: презентация к факультативному занятию
Тема: «13 способов решения квадратного уравнения»
Раздел: полное образование
Алгебра 8 класс
Савельева Ольга Николаевна
г .Стерлитамак, Республики
Презентация к факультативному
занятию по теме
«13 способов решения квадратного
алгебру, часто полезно решить одну и
ту же задачу тремя различными
способами, чем решать три-четыре
различные задачи. Решая одну задачу
различными способами, можно путем
сравнения выяснить, какой из них
короче, эффективнее. Так
1СПОСОБ. Разложение левой
части уравнения на множители.
Решим уравнение х
Разложим левую часть на множители:
х ( х – 1 ) + 5( х – 1 ) = 0
2СПОСОБ. Метод выделения
Решим уравнение х
уравнений по формуле.
+ bх + с = 0, а ≠ 0, имеет корни
Решим уравнение х
= -4- 16-4•1(-5)= -4- 36 = -4-6 = -5
+2kx+c=0, a=0 имеет корни
Решим уравнение x
4СПОСОБ.Решение уравнений с
использованием теоремы Виета.
Его корни удовлетворяют теореме Виета, которая при
Применим этот способ к нашему уравнению
+ bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение
Пусть ах = у, откуда х = ; тогда приходим к уравнению
равносильно данному. Его корни у
помощью теоремы Виета.
Окончательно получаем х
Применим этот способ к нашему
+ 4х –5= 0 , ах = у, а=1.
Рассмотрим другое уравнение
1)Если a+b+c=0, то x
2) Если a-b+c=0, то x
Применим этот способ к нашему
а + b + с = 0, 1 + 4 – 5= 0
7СПОСОБ: Графическое решение
Если в уравнении х
+ рх + q = 0 перенести
второй и третий члены в правую часть, то
1)Если прямая и парабола пересекаются в
двух точках, то уравнение имеет два
2) Если прямая и парабола пересекаются в
одной точке, то уравнение имеет одно
3)Если прямая и парабола не
пересекаются, то уравнение не имеет
Решим графически уравнение х
Прямая и парабола пересекаются в двух точках
уравнений с помощью циркуля и
1)Построим точки S ( -b/2a ; (а+с)
/2a )(центр окружности) и А (0 ;
2)Проведем окружность с
3)Абсциссы точек пересечения
этой окружности с осью ОХ
является корнями исходного
Решим уравнение х
1. Определим координаты точки центра
окружности по формулам:
у = (а+с) /2a =(1+(-5)):2 = — 2
S ( — 2 ; — 2) и А ( 0 ; 1 ).
2. Проведем окружность с R = SA , где А ( 0 ; 1 ).
Абсцисса точек пересечения этой окружности с
9СПОСОБ: Решение квадратных
уравнений с помощью номограммы.
Номограмма даёт значения положительных корней
Если это уравнение имеет корни разных знаков , то ,
найдя по номограмме положительный корень,
отрицательный находят ,вычитая положительный из -p .В
случае ,когда оба корня отрицательны, берут
z=-t и находят по номограмме два положительных корня
коэффициенты p и q выходят за пределы шкал,
выполняют подстановку z=kt и решают посредством
Уравнение, где k берется с таким расчётом, чтобы имели
способ решения квадратных
Решим уравнение х
+ 4х числом 5, получим, что S = 5+ 4 =9.
Применим этот способ к нашему уравнению
11 СПОСОБ. Для нахождения
корней приведённого квадратного
полезно воспользоваться формулой
решения квадратных уравнений
Применим этот способ к нашему уравнению
13СПОСОБ.Альтернативный метод решения
А.В.Борисов, канд.техн.наук, Л.Н.Королевич
Рассмотрим новый метод решения квадрат-
ных уравнений, который применим к приведенным квадратным
atr, btr – длины катетов прямоугольного тре-
угольника (далее просто катеты);
ctr – длина гипотенузы прямоугольного тре-
угольника (далее просто гипотенуза);
αtr, βtr – острые углы против катетов atr и btr
φtr – один из острых углов прямоугольного
треугольника (atr или btr );
mtr – длина медианы, опущенной на гипоте-
нузу (далее просто медиана);
htr – длина высоты, опущенной на гипотенузу
(далее просто высота);
θtr – угол между медианой и высотой;
tr – угол между медианой и гипотенузой.
Для этого необходимо:
1. определить величину угла θ (соответст-
2. определить величину угла
3. определить первый корень:
4. определить второй корень:
Применим этот способ к нашему
Промежуточные величины определяются по формулам
Но как мы видим этот способ нельзя назвать
Решить каждое уравнение несколькими
способами. (Работа в парах)
наиболее удачными способами
Великий Д.Пойа говорил: «Если вы хотите научиться плавать, то
смело входите в воду, а если хотите научиться решать задачи, то
решайте их». Мне хочется продолжить, если хотите научиться
решать уравнения, то решайте их и не просто решайте, а решайте
с вдохновением самым удачным и подходящим способом. Ведь
Г.Лейбниц заметил: «Первое условие, которое надлежит
выполнять в математике, — это быть точным, второе — быть ясным
и, насколько можно, простым». Ваше решение должно приносить
12 способов решения квадратных уравнений
В работе рассматриваются способы решения квадратных уравнений, которых нет в учебнике. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения кваратных уравнений при решении задач обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.
Просмотр содержимого документа
«12 способов решения квадратных уравнений »
1.Определение квадратного уравнения, его виды 4
2. Способы решения квадратных уравнений 4
2.1 Решение неполных квадратных уравнений. 4
2.2 Разложение левой части уравнения на множители. 1. СПОСОБ 5
2.3 Метод выделения полного квадрата. 2. СПОСОБ 5
2.4 Решение квадратных уравнений по формуле. 3. СПОСОБ 5
3.5 Решение уравнений с использованием теоремы Виета. 4. СПОСОБ 6
3.6 Решение уравнений с использованием теоремы Виета 5. СПОСОБ 6
3.7 Решение уравнений способом «переброски». 6. СПОСОБ 6
3.8 Свойства коэффициентов квадратного уравнения. 7. СПОСОБ 7
3.9 Графическое решение квадратного уравнения. 8. СПОСОБ 8
3.10 Решение квадратных уравнений с помощью
циркуля и линейки. 9. СПОСОБ 8
3.11 Решение квадратных уравнений с помощью номограммы. 10. СПОСОБ 9
3.12 Геометрический способ решения квадратных уравнений. 11. СПОСОБ 10
3.13 Способ решения квадратных уравнений по теореме Безу. 12. СПОСОБ 10
Список литературы 12
Приложение 2 ЗАДАЧИ
Приложение 3 Из истории квадратных уравнений
Уравнения второй степени умели решать еще в древнем Вавилоне. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид — при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактах.
Вывод формулы решения квадратного уравнения в общем, виде имеется у Виета. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Впервые квадратное уравнение сумели решить математики Древнего Египта.
Неполные квадратные уравнения и частные виды полных квадратных уравнений 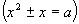
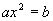
Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. итальянским математиком Леонардом Фибоначчи.
Общее правило решения квадратных уравнений, приведенных к виду 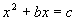
Формулы, выражающие зависимость корней уравнения от его коэффициентов, были выделены Виетом в 1591 г.
И сейчас квадратные уравнения очень актуальны. Одна из основных тем ОГЭ – это квадратные уравнения.
Одной из основных тем, проверяемых на экзамене по математике, является тема «Квадратные уравнения». Данная тема изучается в 8 классе, а на повторение данной темы в 9 классе отводится один час. Я надеюсь , что эта работа поможет сдать экзамен по алгебре на более высокий бал.
Также квадратные уравнения используются в физике и в химии для решения задач в 10 и 11 класса, знание данной темы поможет при сдаче ЕГЭ по этим предметам.
Научиться решать квадратные уравнения различными способами.
Для достижения цели мы поставили перед собой следующие задачи
1.Изучить литературу по выбранной теме;
2.Изучить историю возникновения и решения квадратных уравнений;
3.Изучить способы решения квадратных уравнений разного вида;
4. Подобрать дидактический материал по теме работы
Объект исследования – квадратные уравнения.
При выполнении исследования применялись такие методы, как сравнительный анализ литературы, сбор и обработка фактов с помощью анализа, сравнения и аналогии.
1.Определение квадратного уравнения, его виды.
Определение: Квадратным уравнением называется уравнение вида
где х— переменная, а,b и с-некоторые числа, причем, а ≠ 0.
Коэффициенты а, b, с, различают по названиям: а – первый или старший коэффициент; b – второй или коэффициент при х; с – свободный член, свободен от переменной х.
Квадратное уравнение также называют уравнением второй степени, так как его левая часть есть многочлен второй степени
Квадратное уравнение называют приведенным, если старший коэффициент равен 1; квадратное уравнение называют неприведенным, если старший коэффициент отличен от 1.
х²+рх+q=0 – стандартный вид приведенного квадратного уравнения
кроме приведенных и неприведенных квадратных уравнений различают также полные и неполные уравнения.
Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля.
Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b и с равен нулю.
Обратите внимание: об ах² речи нет, этот член всегда присутствует в квадратном уравнении.

2) ах 2 + bх = 0, где b ≠ 0;
Корнем квадратного уравнения ах²+вх+с=0 называют всякое значение переменной х, при котором квадратный трехчлен ах²+bх+с обращается в нуль; такое значение переменной х называют также корнем квадратного трехчлена.
Можно сказать и так: корень квадратного уравнения ах²+bх+с=0 – это такое значение х, подстановка которого в уравнение обращает уравнение в верное числовое равенство. 0=0.
Решить квадратное уравнение – это значит найти все его корни или установить, что их нет.
2.Способы решения квадратных уравнений
2.1 Решение неполных квадратных уравнений.
Сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать.
http://zhurnalpedagog.ru/servisy/publik/publ?id=8803
http://kopilkaurokov.ru/matematika/uroki/12-sposobov-rieshieniia-kvadratnykh-uravnienii

