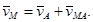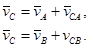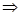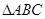Плоскопараллельное движение твердого тела.
1. Уравнения плоскопараллельного движения
Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемешаются параллельно некоторой неподвижной плоскости П.
Рассмотрим сечение S тела какой-нибудь плоскостью Oxy, параллельной плоскости П. При плоскопараллельном движении все точки тела, лежащие на прямой ММ / , перпендикулярны к сечению (S), то есть к плоскости П движутся тождественно и в каждый момент времени имеют одинаковые скорости и ускорения. Поэтому для изучения движения всего тела достаточно изучить, как движется сечение S тела в плоскости Oxy.
(4.1)
Уравнения (4.1) определяют закон происходящего движения и называются уравнениями плоскопараллельного движения твердого тела.
2. Разложение плоскопараллельного движения на поступательное
вместе с полюсом и вращательное вокруг полюса
Покажем, что плоское движение слагается из поступательного и вращательного. Для этого рассмотрим два последовательных положения I и II, которые занимает сечение Sдвижущегося тела в моменты времени t1 и t2= t1 + Δt. Легко видеть, что сечение S, а с ним и все тело можно привести из положения I в положение II следующим образом: переместим сначала тело поступательно, так, чтобы полюс А, двигаясь вдоль своей траектории, пришел в положение А2. При этом отрезок A1B1займет положение , а затем повернем сечение вокруг полюса А2 на угол Δφ1.
Следовательно, плоскопараллельное движение твердого тела слагается из поступательного движения, при котором все точки тела движутся так же как полюс А и из вращательного движения вокруг этого полюса.
При этом следует отметить, что вращательное движение тела происходит вокруг оси, перпендикулярной к плоскости П и проходящей через полюс А. Однако для краткости мы будем в дальнейшем называть это движение просто вращением вокруг полюса А.
Поступательная часть плоскопараллельного движения описывается, очевидно, первыми двумя из уравнений (2. 1), а вращение вокруг полюса А — третьим из уравнений (2. 1).
Основные кинематические характеристики плоского движения
В качестве полюса можно выбирать любую точку тела
Вывод : вращательная составляющая плоского движения от выбора полюса не зависит, следовательно, угловая скорость ω и угловое ускорение e являются общими для всех полюсов и называются угловой скоростью и угловым ускорением плоской фигуры
Векторы и направлены по оси, проходящей через полюс и перпендикулярной плоскости фигуры
 |  |
 |  |
3. Определение скоростей точек тела
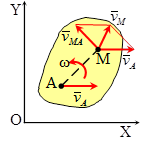
Теорема: скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и вращательной скорости этой точки вокруг полюса.
При доказательстве будем исходить из того, что плоскопараллельное движение твердого тела слагается из поступательного движения, при котором все точки тела движутся со скоростью vА и из вращательного движения вокруг этого полюса. Чтобы разделить эти два вида движения, введем две системы отсчета: Oxy – неподвижную, и Ox1y1 – движущуюся поступательно вместе с полюсом А. Относительно подвижной системы отсчета движение точки М будет «вращательным вокруг полюса А».
Таким образом, скорость любой точки М тела геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости точки М в ее вращательном движении вместе с телом вокруг этого полюса.
Геометрическая интерпретация теоремы
Следствие 1. Проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны друг другу.
 |
 |  |
4. План скоростей
Планом скоростей называется диаграмма, на которой из произвольно выбранного полюса откладываются скорости точек, а вращательные скорости звеньев из плюса не выходят и располагаются перпендикулярно звеньям.
Построение плана скоростей базируется на соотношениях (3.6)
Откуда следует, что отрезки, соединяющие концы векторов скоростей на плане скоростей, перпендикулярны отрезкам, соединяющим соответствующие точки плана, и по модулю пропорциональны этим отрезкам, а их отношение равно угловой скорости плоской фигуры.
(3. 6′)
Плоское движение твердого тела
Движение твердого тела называется плоским(плоскопараллельным), если каждая точка тела движется в одной и той же плоскости.
8.1.1 Свойства плоского движения:
ü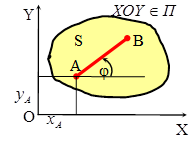 
точки тела движутся в плоскостях параллельных между собой и некоторой фиксированной плоскости П0;
ü траектории точек – плоские кривые;
ü для изучения плоского движения тела достаточно изучить движение плоской фигуры S в сечении плоскостью П÷÷ П0;
ü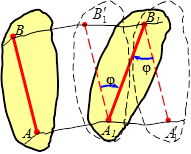 
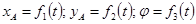
положение плоской фигуры S однозначно определяется положением в этом сечении отрезка АВ; положение отрезка АВ однозначно определяется координатами произвольно выбранной точки А (полюса) и углом φ: 
— уравнения плоского движения твердого тела;
ü движение плоской фигуры S в ее плоскости П может рассматриваться как сумма поступательного движения всех точек фигуры, движущихся как полюс – точка А и вращения фигуры S вокруг этого полюса;
ü поступательное движение полюса и угол поворота φ не зависят от выбора полюса.
8.1.2 Теорема сложения скоростей плоской фигуры:
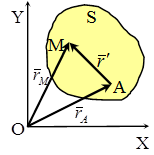
Теорема: Скорость любой точки (М) плоской фигуры геометрически складывается из скорости какой-либо другой точки (А), принятой за полюс и скорости, которую данная точка (М) получит при вращении фигуры вокруг полюса.
Доказательство
Так как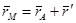 
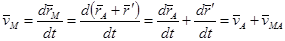
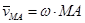
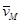
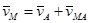
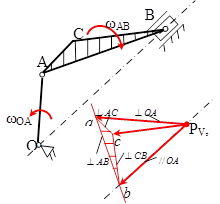
, то
.
Вектор 
и направлен перпендикулярно АМ в сторону указанную угловой скоростью ω. Модуль и направление вектора 
определяют по правилу параллелограмма. Векторное уравнение 
может быть решено аналитически (для этого его проецируют на оси координат) и графически (строят план скоростей, см. ниже).
8.1.3 Планом скоростей называется векторная диаграмма, построенная на основе теоремы сложения скоростей. Покажем порядок построения плана скоростей для кривошипно-ползунного механизма – широко распространенного в сельхозмашиностроении и других отраслях.
Кривошипно-ползунный механизм состоит из трех подвижных звеньев: кривошипа ОА; шатуна АВС; ползуна (поршня) В и неподвижной стойки (заштриховано). Если заданы: положение механизма, угловая скорость кривошипа ωОА, длины звеньев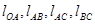 
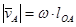
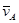
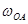
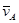
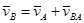
, то можно рассчитать модуль скорости точки А по формуле 
; вектор 
направлен перпендикулярно кривошипу ОА в сторону, указанную 
.
Из произвольной точки РV (полюс плана скоростей) отложим в масштабе вектор , его конец обозначим буквой а. Шатун АВ совершает плоское движение, применим к нему теорему сложения скоростей
.
Из конца вектора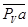 
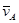
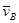
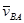
проведем перпендикуляр к АВ, а из полюса плана PV//OB. Точку пересечения обозначим b. Проведем из полюса PV стрелки к точкам a и b. Это в масштабе векторы скоростей и 
. Вектор 
изображен на плане скоростей отрезком ab и направлен от a к b.
Чтобы определить скорость точки С шатуна составим по теореме сложения скоростей два векторных уравнения, приняв за полюсы точки А и В:
Чтобы совместно графически решить эти уравнения, проведем из точки a плана скоростей перпендикуляр к АС, а из точки b перпендикуляр к ВС. Точку их пересечения обозначим с. Стрелка из полюса плана скоростей PV к точке c – в масштабе вектор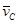 
. План построен.
Свойства плана скоростей:
ü масштаб плана скоростей определяется по заданному вектору скорости (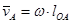 
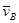
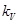
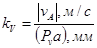
или ) с помощью масштабного коэффициента 
, который рассчитывают разделив модуль заданной скорости на выбранную длину, например, 
;
ü полюс плана скоростей точка PV, в этой точке находятся точки, скорость которых равна нулю (например, неподвижная точка стойки О;
ü скорость любой точки механизма относительно стойки (например, 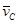) изображается отрезком, направленным от полюса плана PV к соответствующей точке (отрезок Pvc);
ü скорость вращения одной точки какого-либо звена вокруг другой (например, точки С вокруг точки А —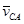 
) изображается одноименным отрезком (ac), направлен вектор к той точке, которую вращают (к точке с);
ü модуль угловой скорости звена равен частному от деления скорости вращения одной точки этого звена вокруг другой на натуральную длину расстояния между точками на звене механизма (например,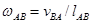 
);
ü модуль любой скорости механизма можно определить, умножив длину соответствующего отрезка на плане скоростей на масштабный коэффициент (например,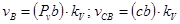 
);
ü если на плане найдены скорости двух точек звена, то скорость любой другой точки этого звена можно найти по правилу подобия: если на звене механизма точки образуют геометрическую фигуру, то одноименные точки на плане скоростей образуют подобную сходственно расположенную (повернутую в плоскости чертежа) фигуру (например, 
).
http://helpiks.org/6-66984.html