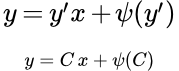2 уравнения лагранжа и клеро

Дифференциальное уравнение Клеро

Решение дифференциального уравнения Клеро

Рассмотрим уравнение Клеро:
(1)
Не трудно убедиться, что его общее решение имеет вид:
(2)

Действительно, поскольку – постоянная, то – тоже постоянная. Тогда дифференцируя (2) имеем:
;
(3) .
Подставляя (2) и (3) в (1), получаем тождество:
.

Особое решение дифференциального уравнения Клеро

Уравнение Клеро может иметь особое решение. Как известно, если общее решение дифференциального уравнения имеет вид:
,
то особое решение может получиться исключением из уравнений:
;
.

В нашем случае, решение (2) можно записать в виде:
.
Тогда
.
Тогда особое решение может получиться, исключением из уравнений:
;
.

Поскольку возможны посторонние решения, то после нахождения особого решения, необходимо проверить, удовлетворяет ли он исходному уравнению (1).

Пример

Решить уравнение:
(1.1)

Это уравнение Клеро. Его общее решение имеет вид:

Ищем особое решение. Перепишем общее решение в виде:
.
Дифференцируем по :

.
Тогда особое решение может получиться исключением из уравнений:
(1.2) ;
(1.3) .

Исключаем . Из уравнения (1.3) имеем:
(1.4) .
Возводим в квадрат и преобразуем:
;
;
. Отсюда следует, что .
Извлекаем квадратный корень:
(1.5) .
Поскольку мы возводили в квадрат, то, возможно, (1.5) содержит лишние решения, которые не удовлетворяют (1.4). Сейчас мы примем (1.5), а отсев лишних решений сделаем в самом конце.
Подставим (1.4) и (1.5) в (1.2):
.

Итак, особые решения имеют вид:
(1.6) .
Теперь сделаем проверку, чтобы выяснить, удовлетворяет ли исходному уравнению (1.1):
(1.1) .
Находим производную (1.6) и выполняем преобразования:

;
;
.
Подставляем в (1.1):
(1.7) .

При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять нижний знак:
.
То есть при , .

При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять верхний знак:
.
То есть при , .

Общее решение уравнения имеет вид:

При уравнение имеет особое решение:
.

При уравнение имеет особое решение:
.

Автор: Олег Одинцов . Опубликовано: 24-08-2012 Изменено: 10-04-2016

Дифференциальные уравнения Лагранжа и Клеро

Автор: Пользователь скрыл имя, 12 Декабря 2011 в 15:59, курсовая работа

Краткое описание

С точки зрения формально-математической задача решения (интегрирования) дифференциальных уравнений есть задача, обратная дифференцированию. Задача дифференциального исчисления состоит в том, чтобы по заданной функции найти её производную. Простейшая обратная задача уже встречается в интегральном исчислении: дана функция f(x), найти её примитивную (неопределённый интеграл).

Файлы: 1 файл

моя курсовая-лагранж и клеро2 — копия.docx

С точки зрения формально- математической задача решения ( интегрирования) дифференциальных уравнений есть задача, обратная дифференцированию. Задача дифференциального исчисления состоит в том, чтобы по заданной функции найти её производную. Простейшая обратная задача уже встречается в интегральном исчислении: дана функция f(x), найти её примитивную (неопределённый интеграл). Если искомую примитивную функцию обозначить через у, то указанная задача может быть записана в форме уравнения:

Равносильные между собой уравнения (1) и (2) являются простейшими дифференциальными уравнениями. Из интегрального исчисления известно, что наиболее общая функция у, удовлетворяющая уравнению (1), или, что то же, уравнению (2), имеет вид:

В решении (3) символ неопределённого интеграла обозначает какую-нибудь примитивную, а С есть произвольное постоянное. Итак, оказывается, что искомая функция y определяется из уравнения (1) или (2) неоднозначно. Наше дифференциальное уравнение имеет бесчисленное множество решений, каждое из которых получится, если произвольному постоянному С придать определённое числовое значение. Решение (3) уравнения (1), содержащее произвольное постоянное, называется общим решением; каждое решение, которое получается из общего, если дать постоянному С определённое числовое значение, называется частным решением.

В уравнение (1) входила только первая производная от искомой функции. Это — дифференциальное уравнение первого порядка. Самое общее дифференциальное уравнение первого порядка имеет вид:

Где F— заданная непрерывная функция трёх своих аргументов; в частности, она может не зависеть от x или от y (или от обоих этих аргументов), но непременно должен содержать . Если уравнение(4) определяет ,как неявную функцию двух остальных аргументов (в дальнейшем мы всегда будем предполагать это условие выполненным), то его можно представить в виде, разрешённом- относительно

Здесь f—непрерывная заданная функция от х, у. В дифференциальном уравнении (4) или (5) х является независимым переменным, у—искомой функцией. Итак, дифференциальное уравнение первого порядка есть соотношение, связывающее искомую функцию, независимое переменное и первую производную от искомой функции.

Решением дифференциального уравнения (4) или (5) называется всякая функция , которая, будучи подставлена в уравнение (4) или (5), обратит его в тождество.

2.Общий метод введения параметра

1.Пусть дано неразрешённое уравнение:

Если мы будем рассматривать х, у, р как декартовы координаты в пространстве, то уравнение (1) определит некоторую поверхность. Известно, что координаты точек поверхности могут быть выражены как функции двух параметров и, v; пусть нам известно такое параметрическое представление поверхности (1):

Система уравнений (5) эквивалентна уравнению (1). Теперь вспомним,

что уравнение (1) дифференциальное и что или

Подставляя в это последнее равенство выражения р, dy, dx, взятые из уравнений (5), получаем:

Это — дифференциальное уравнение первого порядка между u и v.Принимая а за независимую переменную, a v за искомую функцию, можем написать его в виде:

Мы получили уравнение первого порядка, но уже разрешённое относительно производной; если мы найдём его общее решение в виде:

то два первых уравнения (5) дадут:

т. е. общее решение уравнения (1), выраженное в параметрической форме (u-параметр, C—произвольное постоянное). Это преобразование (5) обыкновенно применяется в случае, если уравнение (1) легко разрешается относительно х или у; тогда в представлении (5) за параметры естественно взять у и p или х и p.

Рассмотрим сначала уравнение:

Соотношение dy=pdx, если принять за параметры хи р, даст нам:

Мы получили уравнение между х и р, разрешённое относительно пусть его общее решение будет:

Внося это выражение в формулу (6), получим общее решение искомого уравнения:

Примечание 1. Уравнение (7) можно получить также из уравнения (6), если дифференцировать обе его части по х, причём р рассматривается как функция х, и заменяется через р. Таким образом, мы имеем здесь новый способ сведения уравнения (6) к более простому уравнению (7) при помощи дифференцирования.

Примечание 2. Получив общий интеграл уравнения (7), мы должны помнить, что р в выражении (8) есть вспомогательная переменная; исключив его из (7) и (6), мы получаем общее решение уравнения (6) без дальнейших интеграции. Было бы ошибочным рассматривать равенство (8) как дифференциальное уравнение, полагая в нём , ибо при интеграции этого уравнения вошло бы в решение второе произвольное постоянное, и мы вместо данного уравнения (6) нашли бы решение уравнения второго порядка:

которое получается из уравнения (7), если считать в нём

2. Рассмотрим теперь уравнение:

Можно воспользоваться соотношением , вводя в него в качестве новых вспомогательных переменных у и р; можно также получить уравнение, разрешённое относительно производной от искомой функции дифференцируя обе части уравнения (9) по y и принимая во внимание, что

или при этом мы находим:

Мы получили дифференциальное уравнение между у и р; найдя его общее решение и внеся это выражение на мест р в данное уравнение (9), получим его общий интеграл: . Впрочем, уравнение (9) переходит в уравнение вида (6), если поменять роль переменных х и у.

Изложенные преобразования приводят уравнение, не разрешённое относительно производной, к новому уравнению, которое является разрешённым относительно производной; но это новое уравнение, вообще говоря, не интегрируется в квадратурах. Сейчас мы рассмотрим тип уравнений, не разрешённых относительно производных, в применении к которым метод дифференцирования всегда приводит к уравнению, интегрируемому в квадратурах. Это—уравнение Лагранжа. Так называется уравнение, линейное относительно х и у, т. е. уравнение вида:

где коэффициенты А, В, С—данные дифференцируемые функции производной Разрешая это уравнение относительно y (мы предполагаем, что приводим его к виду:

Применяя к уравнению (10) метод дифференцирования (так как это — уравнение вида (6)), приходим к уравнению (10`)

Если в этом уравнении рассматривать x как искомую функцию, а p — как независимое переменное, то получаем линейное уравнение:

Оно, как известно, интегрируется в квадратурах; решение имеет вид:

где, например . Внося найденное выражение х в данное уравнение, получим выражение вида:

Таким образом, два переменных выражены в функции параметра р; если исключить этот параметр, получим общий интеграл уравнения Лагранжа в форме Ф(х, у, С) = 0.

Примечание Приведение к виду (10″) невозможно, если Допустим теперь, что для некоторого значения р = С₀ мы имеем

. Тогда уравнение (10′), очевидно, допускает решение р = С₀; подставляя в уравнение; (10) это значение p, получаем

Легко проверить, что это есть решение уравнения (10); можно также убедиться в том, что оно не содержится в формуле общего решения.

Уравнения Лагранжа и Клеро

Некоторые дифференциальные уравнения первого порядка приходится решать методом введения вспомогательного параметра. К числу таких уравнений относятся уравнение Лагранжа

и уравнение Клеро

y = x y¢ + y ( y¢), ( 2 )

где j и y – известные функции от y¢.

Заметим, что оба этих уравнения не разрешены относительно производной y¢.

Уравнение Лагранжа (1) интегрируется следующим образом: обозначая р = y¢, запишем уравнение в виде

y = x j (р) + y (р). Дифференцируя полученное уравнение по х, имеем

Уравнение (1) может иметь особое решение вида y = x j(р₀) + y( р₀), где р₀ — корень уравнения р = j (р).

Уравнение Клеро является частным случаем уравнения Лагранжа при j ( y¢) = y¢. Его общее решение имеет вид у = Сх + y (С), особое решение получается путем исключения параметра р из уравнений у = рх + y (р) и

Пример 17. Решить уравнение Клеро у = ху′ + у′ 2 .

Общее решение (см. выше) имеет вид у = сх + с 2 . Особое решение получается путем исключения параметра р из уравнений у = рх + р 2 и х = –2р: у = – 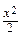+ , т.е. у = – .

Дифференциальные уравнения высших порядков

Основные понятия

Дифференциальное уравнение второго порядка в общем случае записывается в виде

или в виде, разрешенным относительно старшей (второй) производной

Решением ДУ2 (1)–(2) называется любая функция у = j (х), которая при подстановке в это уравнение обращает его в тождество. График функцииу = j (х) называется интегральной кривой.

Задача отыскания решения ДУ(1)–(2), удовлетворяющего заданным начальным условиям у(х₀) = у₀, у¢ (х₀) = у¢₀, где х₀,у₀, у¢ ₀ – некоторые числа, называется задачей Коши. Геометрически это равносильно следующему: требуется найти интегральную кривую уравнения (1)–(2), проходящую через точку М(х₀, у₀) с угловым наклоном касательной в этой точке у¢₀ .

Общим решением уравнения (1)–(2), называется функция у = j (х, С₁, С₂), зависящая от двух произвольных постоянных С₁ и С₂ и такая, что:

1) при любых конкретных значениях С₁ и С₂ она является решением этого уравнения;

2) для любых допустимых начальных условий

можно подобрать такие значения С₁ 0 и С₂ 0 постоянных, что функция у = j (х, С₁ 0 , С₂ 0 ) будет удовлетворять этим начальным условиям.

Частным решением уравнения (1)–(2) называется функция у = j (х, С₁ 0 , С₂ 0 ), получающаяся из общего решения при конкретных значениях постоянных С₁ и С₂.

Геометрически общее решение ДУ2 представляет собой множество интегральных кривых; частное решение – одну из интегральных кривых этого множества.

Аналогичные понятия и определения имеют место для ДУ n–го порядка, которое в общем виде записывается

Начальные условия для ДУ(4):

Общим решениемДУ n–го порядка называется функция вида у = j (х, С₁, С₂, … , С_n), содержащая n произвольных, не зависящих от х, постоянных.

Решение ДУ(4), получающееся из общего решения при конкретных значениях постоянных

Задача Коши дляДУ n–го порядка: найти решение ДУ(4), удовлетворяющее начальным условиям (5).

Проинтегрировать (решить) ДУ n–го порядка означает следующее: найти его общее или частное решение (интеграл) в зависимости от того, заданы начальные условия или нет.

Задача нахождения решения ДУ n–го порядка сложнее, чем первого. Поэтому рассматриваем лишь отдельные виды ДУ высших порядков (≥ 2)

Дата добавления: 2017-11-21 ; просмотров: 1965 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ