Урок устной работы по алгебре в 9-м классе. Тема: «Виды уравнений и способы их решения»
Тема: “Виды уравнений и способы их решения”.
Форма: урок устной работы.
Цели:
- Обучающая: привести в систему знания учащихся по данной теме (повторить теорию, выработать умение определять вид уравнения и выбирать рациональный способ решения данного уравнения);
- Развивающая: интенсивное и творческое мышление, желание поиска решения;
- Воспитывающая: привитие интереса к устной работе, воспитание навыков сознательного усвоения материала.
Ход урока
I. Мотивация.
Историческая справка о возникновении “алгебры” в связи с решением разнообразных задач при помощи уравнений (1 мин.)
II. Повторение теоретического материала.
III. Устная работа.
Решите уравнение, объясняя какого вида уравнение, назовите способ его решения, теоретически обосновывая каждый шаг.
А) Линейные уравнения
1.
3х + (20 – х) = 30 линейное уравнение
3х + 20 –1х = 30 раскрываем скобки, приводим подобные слагаемые
2х + 20 = 30 переносим слагаемые без переменной в правую часть, меняя знак
х = 5 находим значение переменной
2.
7m * 3 = 5 * 2m решается по свойству пропорции
21 m = 10 m переносим слагаемые в левую часть уравнения
21 m – 10 m = 0 приводим подобные члены
11 m = 0 свойство произведения (равенство 0)
3.
( х – 3 ) 2 – х 2 = 7 – 5 х раскрываем скобки
х 2 – 6х + 9 – х 2 = 7 – 5 х приводим подобные слагаемые
– 6х + 9 = 7 – 5 х переносим слагаемые
6х + 5х = 7 – 9 приводим подобные слагаемые
Б) Квадратные уравнения, и уравнения, приводимые к квадратным
1.
z 2 – 10 = 29 неполное квадратное уравнение
z 2 = 39 > 0; 2 корня
z1 =
z2 = –
2.
– х 2 = 13 неполное квадратное уравнение
х 2 = –13 2 – 5 ( х – 4 ) + 6 = 0 уравнение, приводимое к квадратному
по теореме, обратной теореме Виета
решаем обратную подстановку:
4.
х 4 – 13 х 2 + 26 = 0, уравнение биквадратное
x 2 = t, t
0
t 2 – 13 t + 36 = 0
Д = ( –13 ) 2 – 4*36 = 169 – 144 = 25 >0, 2 корня
х 2 = 9 > 0, 2 корня
х 2 =4 > 0 , 2 корня
5.
(x + 2) 2 = t, t 
t 2 – 11 t – 12 = 0
по теореме, обратной теореме Виета:
t1 t2 = –12, следовательно t1 = 12 
t2 = –1 – посторонний корень
Решаем обратную подстановку:
Д = 48 > 0, 2 корня
х1, 2 = ( –4 + 4
х1, 2 = –2 + 2
В) Уравнения высших степеней
1.
х 2 ( 1 – х ) = 0, следовательно х = 0 или 1 – х = 0 х = 1
2.
разделим обе части на 3:
y =
3.
( х 3 + х 2 ) + ( х + 1) = 0
х 2 (х + 1) + ( х+ 1) =0
( х+ 1) (х 2 +1) = 0, следовательно х + 1 = 0 или х 2 + 1 = 0
х = –1 х 2 = –1 2 = 64
2.
2 а – 5 
2 * 15 – 5 = 25
0
Е) Уравнения с модулем
х 2 – 5х = 0, если х > 0
если х 
Ж) Уравнения с параметрами
IV. Устная самостоятельная работа с последующей проверкой (уровневая)
Задание: Решите уравнение, фиксируя на листе только ответы.
“А” ( на оценку “3”)
“Б” (на “4”)
(х 2 – 1) 2 – 11 ( х 2 – 1) + 24 = 0
х 7 + х 6 + х + 1 = 0
(х + 5) (х – 6/7) (х + 1/3) (х –8) = 0
“В” ( на “5”)
1. ( х 2 –2) 2 – 9 (х 2 – 2 ) + 14 = 0
3. х 5 + х 4 + х + 1 = 0
V. Итоги урока Виды уравнений; Способы решения; Активность учащихся, оценка устной работы.
VI. Домашнее задание
Индивидуальные карточки с наборами уравнений.
Виды уравнений и методы их решения
В разработке рассматриваются виды алгебраических уравнений и методы их решения.
Просмотр содержимого документа
«Виды уравнений и методы их решения»
Виды уравнений и методы их решения
Уравнения подразделяются на две большие группы: алгебраические и трансцендентные. Алгебраическим называется такое уравнение, в котором для нахождения корня уравнения используются только алгебраические действия, а именно четыре арифметических – сложение, вычитание, умножение и деление, а также возведение в степень и извлечение натурального корня. Трансцендентным называется уравнение, в котором для нахождения корня используются не алгебраические функции: например, тригонометрические, логарифмические и иные.
В курсе математики основной школы рассматриваются только алгебраические уравнения. Рассмотрим более подробно их виды и алгоритм решения.
Группу алгебраических уравнений можно условно разделить на такие виды уравнений как:
целые — с обеими частями, состоящими из целых алгебраических выражений по отношению к неизвестным;
дробные — содержащие целые алгебраические выражения в числителе и знаменателе;
иррациональные — алгебраические выражения здесь находятся под знаком корня.
Дробные и иррациональные уравнения можно свести к решению целых уравнений.
Существует также и ещё одна классификация, которая основывается на степени, которая имеется в левой части многочлена. Исходя из этого различают линейные, квадратные и кубические уравнения. Линейные уравнения также могут называться уравнениями первой степени, квадратные — второй, а кубические, соответственно, третьей.
Рассмотрим особенности решения алгебраических уравнений
В алгебре рассматриваются два вида равенств – тождества и уравнения.
Остановимся на основных понятиях.
Тождество — это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв. Для записи тождества наряду со знаком 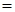
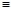
Уравнение — это равенство, которое выполняется лишь при некоторых значениях входящих в него букв. Буквы, входящие в уравнение, по условию задачи могут быть неравноправны: одни могут принимать все свои допустимые значения (их называют параметрами или коэффициентами уравнения и обычно обозначают первыми буквами латинского алфавита:a, b, c. – или теми же буквами, снабженными индексами: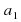
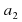
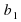
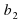
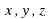
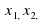
В общем виде уравнение может быть записано так:
F (
В зависимости от числа неизвестных уравнение называют уравнением с одним, двумя и т. д. неизвестными.
Значение неизвестных, обращающие уравнение в тождество (верное равенство), называют решениями уравнения.
Решить уравнение – это значит найти множество его решений или доказать, что решений нет. В зависимости от вида уравнения множество решений уравнения может быть бесконечным, конечным и пустым.
Если все решения одного уравнения являются решениями другого уравнения, то такие уравнения называют эквивалентными.
Рассмотрим некоторые эквивалентные уравнения:
Уравнение 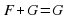
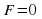
Уравнение 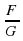
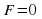
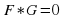
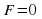
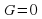
Уравнение 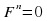
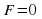
Уравнение 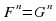
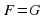
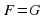
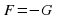
Алгебраическим уравнением называется уравнение вида 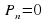
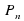
Алгебраическим уравнением с одним неизвестным называется уравнение, сводящееся к уравнению вида:
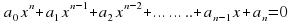
где n – неотрицательное целое число; коэффициенты многочлена называются , ……коэффициентами (или параметрами), называется неизвестным и является искомым. Число n называется степенью уравнения.
Значения неизвестного , обращающие алгебраическое уравнение в тождество, называются корнями (решениями) алгебраического уравнения.
Есть несколько видов уравнений, которые решаются по готовым формулам. Это линейное и квадратное уравнения, а также уравнения вида , где F – одна из стандартных функций (степенная или показательная функция, логарифм, синус, косинус, тангенс или котангенс). Такие уравнения считаются простейшими. Так же существуют формулы и для кубического уравнения, но его к простейшим не относят.
Главная задача при решении любого уравнения – свести его к простейшим.
Все ниже перечисленные уравнения имеют так же и свое графическое решение, которое заключается в том, чтобы представить левую и правую части уравнения как две одинаковые функции от неизвестного. Затем строится график сначала одной функции, а затем другой и точка (и) пересечения двух графиков даст решение (я) исходного уравнения. Примеры графического решения всех уравнений даны в приложении.
Рассмотрим методы решения уравнений.
Линейным уравнением называется уравнение первой степени.
где a и b – некоторые действительные числа.
Линейное уравнение всегда имеет единственный корень , который находится следующим образом.
Прибавляя к обеим частям уравнения (1) число -b, получаем уравнение
, (2) эквивалентное уравнению (1). Разделив обе части уравнения (2) на величину , получаем корень уравнения (1):
Алгебраическое уравнение второй степени (3),
где a, b, с– некоторые действительные числа, называется квадратным уравнением.
Если , то квадратное уравнение (3) называется приведенным.
Корни квадратного уравнения вычисляются по формуле
Выражение называется дискриминантом квадратного уравнения.
если , то уравнение имеет два различных действительных корня;
если , то уравнение имеет один действительный корень кратности 2;
если , то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня:
Частными видами квадратного уравнения (3) являются:
1) Приведенное квадратное уравнение (в случае, если ), которое обычно записывается в виде
Корни приведенного квадратного уравнения вычисляются по формуле
Эту формулу называют формулой Виета – по имени французского математика конца XVI в., внесшего значительный вклад в становление алгебраической символики.
2) Квадратное уравнение с четным вторым коэффициентом, которое обычно записывается в виде
Корни этого квадратного уравнения удобно вычислять по формуле
Формулы (4) и (5) являются частными видами формулы для вычисления корней полного квадратного уравнения.
Корни приведенного квадратного уравнения
связаны с его коэффициентами Формулами Виета
В случае, если приведенное квадратное уравнение имеет действительные корни, формулы Виета позволяют судить как о знаках, так и об относительной величине корней квадратного уравнения, а именно:
если , , то оба корня отрицательны;
если , , то оба корня положительны;
если , , то уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине больше положительного;
если , , уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине меньше положительного корня.
Перепишем еще раз квадратное уравнение
и покажем еще один способ как можно вывести корни квадратного уравнения (6) через его коэффициенты и свободный член. Если
то корни квадратного уравнения вычисляются по формуле
которая может быть получена в результате следующих преобразований исходного уравнения, а так же с учетом формулы (7).
Заметим, что , поэтому
но , из формулы (7) поэтому окончательно
Если положить, что + , то
Заметим, что , поэтому
но , поэтому окончательно
Уравнения n-й степени вида
называется двучленным уравнением. При и заменой (2))
где — арифметическое значение корня, уравнение (8) приводится к уравнению
которое и будет далее рассматриваться.
Двучленное уравнение при нечетном n имеет один действительный корень . В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и комплексных):
Двучленное уравнение при четном n в множестве действительных чисел имеет два корня , а в множестве комплексных чисел n корней, вычисляемых по формуле (9).
Двучленное уравнение при четном n имеет один действительный корней , а в множестве комплексных чисел корней, вычисляемых по формуле
Двучленное уравнение при четном n имеет действительный корней не имеет. В множестве комплексных чисел уравнение имеет корней, вычисляемых по формуле (10).
Приведем краткую сводку множеств корней двучленного уравнения для некоторых конкретных значений n.
Уравнение имеет два действительных корня .
Уравнение имеет один дествительный корень и два комплексных корня
Уравнение имеет два действительных корния и два комплексных корня .
Уравнение действительных корней не имеет. Комплексные корни: .
Уравнение имеет один дествительный корень и два комплексных корня
Уравнение действительных корней не имеет. Комплексные корни:
Если квадратные уравнения умели решать еще математики Вавилонии и Древней Индии, то кубические, т.е. уравнения вида
оказались «крепким орешком». В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности» задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.
Начнем с упрощения
Если кубическое уравнение общего вида
разделить на , то коэффициент при станет равен 1. Поэтому в дальнейшем будем исходить из уравнения
Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:
Чтобы не путаться в коэффициентах, заменим здесь на и перегруппируем слагаемые:
Мы видим, что надлежащим выбором , а именно взяв , можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при и свободным членом. Сложим уравнения (11) и (12) и приведем подобные:
Если здесь сделать замену , получим кубическое уравнение относительно без члена с :
Итак, мы показали, что в кубическом уравнении (11) с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида
Давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:
Сравните эту запись с уравнением (13) и попробуйте установить связь между ними. Даже с подсказкой это непросто. Надо отдать должное математикам эпохи Возрождения, решившим кубическое уравнение, не владея буквенной символикой. Подставим в нашу формулу :
Теперь уже ясно: для того, чтобы найти корень уравнения (13), достаточно решить систему уравнений
и взять в качестве сумму и . Заменой , эта система приводится к совсем простому виду:
Дальше можно действовать по-разному, но все «дороги» приведут к одному и тому же квадратному уравнению. Например, согласно теореме Виета, сумма корней приведенного квадратного уравнения равна коэффициенту при со знаком минус, а произведение – свободному члену. Отсюда следует, что и — корни уравнения
Выпишем эти корни:
Переменные и равны кубическим корням из и , а искомое решение кубического уравнения (13) – сумма этих корней:
Эта формула известная как формула Кардано.
подстановкой приводится к «неполному» виду
Корни , , «неполного» кубичного уравнения (14) равны
Пусть «неполное» кубичное уравнение (14) действительно.
а) Если («неприводимый» случай), то и
Во всех случаях берется действительное значение кубичного корня.
Алгебраическое уравнение четвертой степени.
где a, b, c – некоторые действительные числа, называется биквадратным уравнением. Заменой уравнение сводится к квадратному уравнению с последующим решением двух двучленных уравнений и ( и — корни соответствующего квадратного уравнения).
Если и , то биквадратное уравнение имеет четыре действительных корня:
Если , (3)), то биквадратное уравнение имеет два действительных корня и мнимых сопряженных корня:
Если и , то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:
Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари.
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени
можно избавиться от члена подстановкой . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
Идея Феррари состояла в том, чтобы представить уравнение в виде , где левая часть – квадрат выражения , а правая часть – квадрат линейного уравнения от , коэффициенты которого зависят от . После этого останется решить два квадратных уравнения: и . Конечно, такое представление возможно только при специальном выборе параметра . Удобно взять в виде , тогда уравнение перепишется так:
Правая часть этого уравнения – квадратный трехчлен от . Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
Это уравнение называется резольвентным (т.е. «разрешающим»). Относительно оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень . При правая часть уравнения (15) принимает вид
а само уравнение сводится к двум квадратным:
Их корни и дают все решения исходного уравнения.
Решим для примера уравнение
Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде
и добавим к обеим частям выражение , чтобы в левой части образовался полный квадрат:
Теперь приравняем к нулю дискриминант правой части уравнения:
или, после упрощения,
Один из корней полученного уравнения можно угадать, перебрав делители свободного члена: . После подстановки этого значения получим уравнение
откуда . Корни образовавшихся квадратных уравнений — и . Разумеется, в общем случае могут получиться и комплексные корни.
подстановкой приводится к «неполному» виду
Корни , , , «неполного» уравнения четвертой степени (16) равны одному из выражений
в которых сочетания знаков выбираются так, чтобы удовлетворялось условие
причем , и — корни кубичного уравнения
Уравнения высоких степеней
Разрешимость в радикалах
Формула корней квадратного уравнения известна с незапамятных времен, а в XVI в. итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Таким образом, было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции (сложение, вычитание, умножение, деление) и извлечение корней степени, не превышающей степень уравнения. Более того, все уравнения данной степени ( ) можно «обслужить» одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные.
После этого естественно возник вопрос: а есть ли похожие общие формулы для решения уравнений пятой степени и выше? Ответ на него смог найти норвежский математик Нильс Хенрик Абель в начале XIX в. Чуть раньше этот результат был указан, но недостаточно обоснован итальянцем Паоло Руффини. Теорема Абеля-Руффини звучит так:
Общее уравнение степени при неразрешимо в радикалах.
Таким образом, общей формулы, применимой ко всем уравнениям данной степени , не существует. Однако это не значит, что невозможно решить в радикалах те или иные частные виды уравнений высоких степеней. Сам Абель нашел такое решение для широкого класса уравнений произвольно высокой степени – так называемых абелевых уравнений. Теорема Абеля-Руффини не исключает даже и того, что корни каждого конкретного алгебраического уравнения можно записать через его коэффициенты с помощью знаков арифметических операций и радикалов, в частности, что любое алгебраическое число, т.е. корень уравнения вида
с целыми коэффициентами, можно выразить в радикалах через рациональные числа. На самом деле такое выражение существует далеко не всегда. Это следует из теоремы разрешимости алгебраических уравнений, построенной выдающимся французским математиком Эваристом Галуа в его «Мемуаре об условиях разрешимости уравнений в радикалах» (1832 г.; опубликован в 1846 г.).
Подчеркнем, что в прикладных задачах нас интересует только приближенные значения корней уравнения. Поэтому его разрешимость в радикалах здесь обычно роли не играет. Имеются специальные вычислительные методы, позволяющие найти корни любого уравнения с любой наперед заданной точностью, ничуть не меньшей, чем дают вычисления по готовым формулам.
Уравнения, которые решаются
Хотят уравнения высоких степеней в общем случае неразрешимы в радикалах, да и формулы Кардано и Феррари для уравнений третьей и четвертой степеней в школе не проходят, в учебниках по алгебре, на вступительных экзаменах в институты иногда встречаются задачи, где требуется решить уравнения выше второй степени. Обычно их специально подбирают так, чтобы корни уравнений можно было найти с помощью некоторых элементарных приемов.
В основе одного из таких приемов лежит теорема о рациональных корнях многочлена:
Если несократимая дробь является корнем многочлена с целыми коэффициентами, то ее числитель является делителем свободного члена , а знаменатель — делителем старшего коэффициента .
Для доказательства достаточно подставить в уравнение и умножить уравнение на . Получим
Все слагаемые в левой части, кроме последнего, делятся на , поэтому и делится на , а поскольку и — взаимно простые числа, является делителем . Доказательство для аналогично.
С помощью этой теоремы можно найти все рациональные корни уравнения с целыми коэффициентами испытанием конечного числа «кандидатов». Например, для уравнения
старший коэффициент которого равен 1, «кандидатами» будут делители числа –2. Их всего четыре: 1, -1, 2 и –2. Проверка показывает, что корнем является только одно из этих чисел: .
Если один корень найден, можно понизить степень уравнения. Согласно теореме Безу,
остаток от деления многочлена на двучлен равен , т. е. .
Из теоремы непосредственно следует, что
Если — корень многочлена , то многочлен делится на , т. е. , где — многочлен степени, на 1 меньшей, чем .
Продолжая наш пример, вынесем из многочлена
множитель . Чтобы найти частное , можно выполнить деление «уголком»:
Алгебра. Урок 4. Уравнения, системы уравнений
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Уравнения”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Линейные уравнения
Линейные уравнения
Линейное уравнение – уравнение вида a x = b , где x – переменная, a и b некоторые числа, причем a ≠ 0 .
Примеры линейных уравнений:
- 3 x = 2
- 2 7 x = − 5
Линейными уравнениями называют не только уравнения вида a x = b , но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.
Как же решать уравнения, которые приведены к виду a x = b ? Достаточно поделить левую и правую часть уравнения на величину a . В результате получим ответ: x = b a .
Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.
Для того, чтобы решить линейное уравнение , необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида a x = b . Решение данного линейного уравнения: x = b a .
Примеры решения линейных уравнений:
- 2 x + 1 = 2 ( x − 3 ) + 8
Это линейное уравнение, так как переменная стоит в первое степени.
Попробуем преобразовать его к виду a x = b :
Для начала раскроем скобки:
2 x + 1 = 4 x − 6 + 8
В левую часть переносятся все слагаемые с x , в правую – числа:
Теперь поделим левую и правую часть на число ( -2 ) :
− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5
Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.
Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:
x 2 + 3 x − 8 = x − 1
Это уравнение не является линейным уравнением.
Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)
- 2 x − 4 = 2 ( x − 2 )
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 2 x = − 4 + 4
И как же здесь искать x , если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом. Запишем ответ к данном линейному уравнению.
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 4 = 2 x − 16
2 x − 2 x = − 16 + 4
В результате преобразований x сократился, но в итоге получилось неверное равенство, так как . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x , при которых равенство становилось бы верным. Запишем ответ к данному линейному уравнению.
Квадратные уравнения
Квадратное уравнение – уравнение вида a x 2 + b x + c = 0, где x – переменная, a , b и c – некоторые числа, причем a ≠ 0 .
Алгоритм решения квадратного уравнения:
- Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: a x 2 + b x + c = 0
- Выписать, чему равны в числах коэффициенты: a = … b = … c = …
- Вычислить дискриминант по формуле: D = b 2 − 4 a c
- Если D > 0 , будет два различных корня, которые находятся по формуле: x 1,2 = − b ± D 2 a
- Если D = 0, будет один корень, который находится по формуле: x = − b 2 a
- Если D 0, решений нет: x ∈ ∅
Примеры решения квадратного уравнения:
- − x 2 + 6 x + 7 = 0
a = − 1, b = 6, c = 7
D = b 2 − 4 a c = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64
D > 0 – будет два различных корня:
x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7
Ответ: x 1 = − 1, x 2 = 7
a = − 1, b = 4, c = − 4
D = b 2 − 4 a c = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0
D = 0 – будет один корень:
x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2
a = 2, b = − 7, c = 10
D = b 2 − 4 a c = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31
D 0 – решений нет.
Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b = 0, либо с = 0, либо b = с = 0 ). Смотрите видео, как решать такие квадратные уравнения!
Разложение квадратного трехчлена на множители
Квадратный трехчлен можно разложить на множители следующим образом:
a x 2 + b x + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )
где a – число, коэффициент перед старшим коэффициентом,
x – переменная (то есть буква),
x 1 и x 2 – числа, корни квадратного уравнения a x 2 + b x + c = 0 , которые найдены через дискриминант.
Если квадратное уравнение имеет только один корень , то разложение выглядит так:
a x 2 + b x + c = a ⋅ ( x − x 0 ) 2
Примеры разложения квадратного трехчлена на множители:
- − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7
− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )
- − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2
− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2
Если квадратный трехчлен является неполным, ( ( b = 0 или c = 0 ) то его можно разложить на множители следующими способами:
- c = 0 ⇒ a x 2 + b x = x ( a x + b )
- b = 0 ⇒ применить формулу сокращенного умножения для разности квадратов.
Дробно рациональные уравнения
Пусть f ( x ) и g ( x ) – некоторые функции, зависящие от переменной x .
Дробно рациональное уравнение – это уравнение вида f ( x ) g ( x ) = 0 .
Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.
ОДЗ – область допустимых значений переменной.
В выражении вида f ( x ) g ( x ) = 0
ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).
Алгоритм решения дробно рационального уравнения:
- Привести выражение к виду f ( x ) g ( x ) = 0 .
- Выписать ОДЗ: g ( x ) ≠ 0.
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни.
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Пример решения дробного рационального уравнения:
Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.
Решение:
Будем действовать в соответствии с алгоритмом.
- Привести выражение к виду f ( x ) g ( x ) = 0 .
Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:
x 2 − 4 2 − x − 1 \ 2 − x = 0
x 2 − 4 2 − x − 2 − x 2 − x = 0
x 2 − 4 − ( 2 − x ) 2 − x = 0
x 2 − 4 − 2 + x 2 − x = 0
x 2 + x − 6 2 − x = 0
Первый шаг алгоритма выполнен успешно.
Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни:
x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.
a = 1, b = 1, c = − 6
D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25
D > 0 – будет два различных корня.
x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Корни, полученные на предыдущем шаге:
Значит, в ответ идет только один корень, x = − 3.
Системы уравнений
Системой уравнений называют два уравнения с двумя неизвестными (как правило, неизвестные обозначаются x и y ) , которые объединены в общую систему фигурной скобкой.
Пример системы уравнений
Решить систему уравнений – найти пару чисел x и y , которые при подстановке в систему уравнений образуют верное равенство в обоих уравнениях системы.
Существует два метода решений систем линейных уравнений:
- Метод подстановки.
- Метод сложения.
Алгоритм решения системы уравнений методом подстановки:
- Выразить из любого уравнения одну переменную через другую.
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
- Решить уравнение с одной неизвестной.
- Найти оставшуюся неизвестную.
Решить систему уравнений методом подстановки
Решение:
- Выразить из любого уравнения одну переменную через другую.
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
- Решить уравнение с одной неизвестной.
3 ( 8 − 2 y ) − y = − 4
y = − 28 − 7 = 28 7 = 4
- Найти оставшуюся неизвестную.
x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0
Ответ можно записать одним из трех способов:
Решение системы уравнений методом сложения.
Метод сложения основывается на следующем свойстве:
Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.
Решить систему уравнений методом сложения
Давайте избавимся в данном примере от переменной x . Суть метода состоит в том, чтобы в первом и во втором уравнении перед переменной x стояли противоположные коэффициенты. Во втором уравнении перед x стоит коэффициент 3 . Для того, чтобы метод сложения сработал, надо чтобы перед переменной x оказался коэффициент ( − 3 ) . Для этого домножим левую и правую часть первого уравнения на ( − 3 ) .
Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.
( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )
− 3 x − 6 y + 3 x − y = − 24 − 4
y = − 28 − 7 = 28 7 = 4
Осталось найти переменную x . Для этого подставим y = 4 в любое из двух уравнений системы. Например, в первое.
Ответ можно записать одним из трех способов:
Задание №9 из ОГЭ 2020. Типовые задачи и принцип их решения.
http://multiurok.ru/files/vidy-uravnienii-i-mietody-ikh-rieshieniia.html
http://epmat.ru/modul-algebra/urok-4-uravneniya-sistemy-uravnenij/




