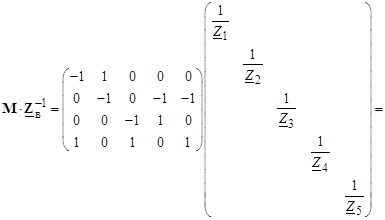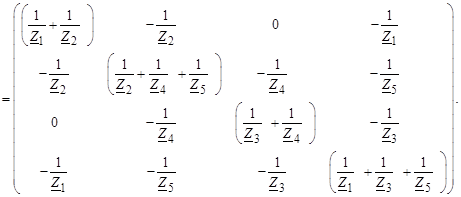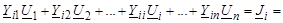4 узловые уравнения установившегося режима

Узловые уравнения установившегося режима

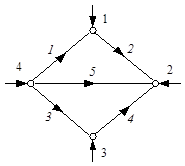
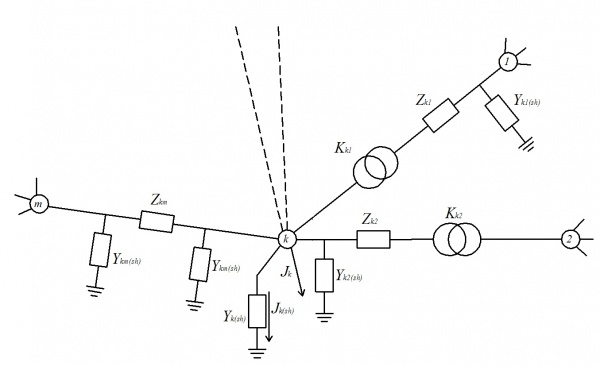
Рассмотрим пример направленного графа электрической сети, изображенного на рис. 3.10.

Для удобства записи в матричной форме параметров ветвей присвоим каждой ветви ее порядковый номер (на рис. 3.10 курсив). Составим матрицу соединений M для этого графа:

(3.10)

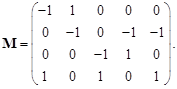
Рис. 3.10. Пример графа
электрической сети

Умножим эту матрицу на матрицу токов ветвей, будем иметь:

(3.11)

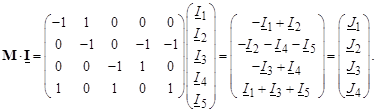
Полученное соотношение является первым законом Кирхгофа в матричной форме записи

(3.12)

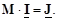
Так как к узлам графа электрической сети еще присоединены другие поперечные ветви с ЭДС и проводимостью шунта, то задающий ток в (3.12) включает в себя также токи данных ветвей

(3.13)

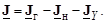
Здесь: J_г – матрица токов генерации (ветви с ЭДС), которые определяются через мощности генерации;

J_н – матрица токов нагрузки, которые определяются через мощности нагрузки (имеет обратное направление – от узла);

J_Y – матрица токов в проводимостях шунтов, которые зависят от проводимости шунта из матрицы Y_N и напряжения в узле из матрицы U (также имеет обратное направление – от узла, так как моделирует потребление мощности).

Умножим транспонированную матрицу соединений М T на матрицу узловых напряжений, получим:

(3.14)

. (3.15)

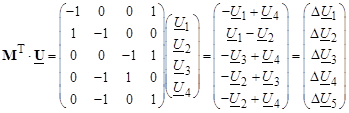
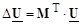
По закону Ома в матричной форме записи имеем

(3.16)

(3.17)

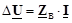
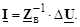
Подставим в (3.12) выражение для матрицы токов ветвей (3.17) и затем (3.15), получим

(3.18)

(3.19)

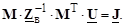
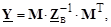
тогда (3.18) приобретет вид

(3.20)

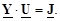
Полученное соотношение является уравнением узловых напряжений (потенциалов) в матричной форме записи. Матрицу Y называют матрицей узловых проводимостей электрической сети. Рассмотрим структуру этой матрицы, для чего выполним матричные перемножения в (3.19). Заметим, что обратная матрица сопротивлений ветвей легко получается в силу своего диагонального вида – ее элементы суть обратные величины к сопротивлениям ветвей и являются проводимостями продольных ветвей.

Вначале перемножим первые две матрицы матричного произведения (3.19):

. (3.21)

Полученную матрицу умножим справа на матрицу M T . В результате получим:

Из полученной матрицы можно сделать следующие выводы о вычислении ее элементов.

1. Элементы, расположенные на главной диагонали матрицы, вычисляются как сумма проводимостей ветвей, подходящих к соответствующему узлу:

(3.23)

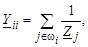
где Y_ii – диагональный элемент матрицы Y;

w_i – множество номеров узлов, связанных с i-м узлом.

2. Недиагональные элементы равны проводимостям ветвей, имя каждой из которых состоит из номеров узлов, соответствующих номеру строки и номеру столбца, на пересечении которых находится данный элемент, и взятых с противоположным знаком. Матрица Y является симметричной матрицей.

(3.24)

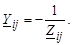
Запишем уравнение узловых напряжений для узла с номером i:

(3.25)

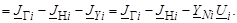
Объединив подобные члены, получим, что в диагональные элементы матрицы Y войдут дополнительные слагаемые Y_Ni:

(3.26)

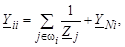
т. е. диагональный элемент будет равен сумме проводимостей всех подходящих к i-му узлу ветвей, включая поперечную ветвь – шунт Y_Ni.

Задающие токи узлов в (3.20) будут состоять только из токов генерации и токов нагрузки.

В случае отсутствия связей с нейтральной плоскостью N система уравнений (3.20) не имеет единственного решения, так как в этом случае определитель матрицы Y равен нулю. Сумма всех задающих токов в такой сети равна нулю:

(3.27)

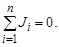
Следовательно, среди всех n узлов можно выделить узел, например с номером n, ток в котором равен

(3.28)

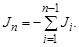
Для уравнений узловых напряжений это означает, что одно уравнение лишнее, т. е. зависит от остальных уравнений и может быть получено через сумму всех остальных уравнений. Так как ток в этом узле может быть получен из баланса токов в сети (3.28), то его называют балансирующим. Обычно это шины мощной электростанции или системы.

Таким образом, из системы (2.20) исключается одно уравнение и тогда получается система независимых линейных уравнений порядка
n – 1. Однако, поскольку число неизвестных напряжений по-прежнему равно n, в одном из узлов следует задать напряжение по величине и фазе так, чтобы все напряжения вычислялись относительно этого известного напряжения. Такой узел в сети называется базисным. Обычно фазу напряжения базисного узла принимают равной нулю, т. е. вектор напряжения базисного узла совмещают с действительной осью. Остальные узлы называют независимыми узлами.

Во многих случаях балансирующий узел и базисный узел совмещают, и в дальнейшем будем считать, что это один и тот же узел.

Таким образом, с исключением уравнения для базисного балансирующего узла с номером n будем иметь систему уравнений (3.20) с числом уравнений n – 1, однако в эти уравнения будет входить слагаемое с заданным напряжением базисного узла.

Изменим номер базисного балансирующего узла. Пусть его номер есть 0 (ноль). Тогда уравнение (3.20) приобретет следующий вид:

(3.29)

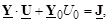
где Y₀ – матрица проводимостей ветвей, связывающих независимые узлы с базисным балансирующим узлом;

U₀ – напряжение базисного узла (скаляр).

Матрица узловых проводимостей в (3.29) имеет порядок n – 1 и определется через матрицу инциденций M, в которой нет одной строки, соответствующей балансирующему узлу.

Необходимо заметить, что во всех уравнениях, где одновременно присутствуют токи и напряжения (3.16), (3.17), (3.18), (3.20), (3.25) и (3.29), напряжения даны в фазных значениях, хотя индекс (буква «ф») для простоты не записывался. Эти же уравнения можно считать записанными и для линейных напряжений, однако токи будут увеличенными в раз, и для вычисления истинных токов их следует уменьшать в .

Дата добавления: 2015-03-19 ; просмотров: 1398 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Уравнения узловых напряжений

Уравнения узловых напряжений (УУН) — система нелинейных (иногда линейных) алгебраических уравнений, в которых неизвестными являются напряжения в узлах электрической сети, наиболее часто применяемая для расчёта установившегося режима электрической сети.

Содержание

Описание

Установившийся режим электрических систем можно рассчитывать при различных способах задания исходных данных в зависимости от физической сути и цели расчёта. В статье рассмотрен наиболее часто встречающийся и наиболее простой случай, когда известны сопротивления и проводимости всех пассивных элементов электрической сети. Кроме того, заданы постоянные величины всех значений токов (мощности) во всех узлах, кроме балансирующего и все ЭДС, а также напряжение одного узла — базисного. При этом необходимо определить напряжения всех [math](n-1)[/math] узлов и токи во всех m ветвях.

В общем случае базисный по напряжению и балансирующий узлы могут не совпадать. Как правило, при расчётах режимов электрических систем предполагают, что эти узлы совпадают, в дальнейшем для простоты изложения предполагается, что базисным по напряжению и балансирующим является один и тот же [math]n[/math] -й узел. Число независимых уравнений по первому закону Кирхгофа равно числу независимых узлов [math](n-1)[/math] . Уравнение первого закона Кирхгофа для [math]n[/math] -го узла является следствием уравнений для остальных [math](n-1)[/math] узлов и не входит в число независимых уравнений.

Если в качестве неизвестных принять [math](n-1)[/math] узловых напря¬жений, то установившийся режим можно описать только узловыми уравнениями, вытекающими из первого закона Кирхгофа и закона Ома [1] , [2] , [3] , [4] . Уравнения узловых напряжений следуют из первого закона Кирхгофа, если все токи в ветвях выразить через узловые напряжения и проводимости ветвей. Число уравнений узловых напряжений равно числу независимых узлов [math](n-1)[/math] .

Уравнения баланса токов представляют собой простейшую форму уравнений, описывающих установившиеся режимы. Существуют две математические модели уравнений узловых напряжений:

Отличительной особенностью этих моделей является то, что линейная модель предполагает задание комплексных значений токов, в отличие от нелинейной модели, которая предполагает задание активной и реактивной мощностей. В большинстве задач нагрузки в узлах задаются активной и реактивной мощностями, по этой причине обычно используется нелинейная модель.

Вывод уравнений узловых напряжений

Для формирования УУН рассмотрим представленную на рис. 1 часть схемы замещения:

Первый закон Кирхгофа для к-го узла:

Наличие знака сопряжения в этом выражении обусловлено тем, что для идеального двухобмоточного трансформатора выполняется закон сохранения мощности [math]\dot=\dot=\hat\dot=\hat\dot[/math] , где индексами «Н» и «В» обозначены соответственно низшая и высшая обмотки трансформатора, поэтому, если [math]\dot=\dot\dot>[/math] , то из закона сохранения следует:

Подстановка полученных выражений в уравнение (1.1) с приведением подобных членов позволяет получить уравнение для k-го узла в виде:

В прямоугольной системе координат

В данной системе комплексные величины [math]\displaystyle \underline_, \dot>, \dot>[/math] представляются в виде

для проводимости справедливо следующее:

получаем, что [math]\displaystyle \underline=g-jb,[/math]

но для удобства расчёта матрицы проводимостей будем использовать соотношение

Запишем УУН для линейной ЭЭС:

левая часть данной системы характеризует токи, втекающие в k-й узел, правая часть — токи, вытекающие из того же узла, но с учетом влияния токов базы.

Подставляем (1), (2), (3) в (4), [math]\dot_б[/math] представим аналогично уравнению (1), тогда имеем следующее:

[math]\displaystyle \begin \sum_^ \left( g_ + j b_ \right) \left( U_‘ + j U_» \right) = J_‘ + j J_»- \left( g_ + j b_ \right) \left(U_<б>‘ + j U_<б>»\right), i = 1 \ldots N \end.[/math]

Сгруппируем и приведем подобные:

Сгруппируем относительно [math]j[/math] левую и правую части системы (5). Два комплексных числа равны, если равны их действительные и мнимые составляющие. Распишем в новой системе отдельно действительные и мнимые части. Получаем:

Представим данную систему (6) в матричной форме:

В случае, если [math]\dot_б=U_б+j0,[/math] система (6) преобразуется к виду:

Соответственно упрощается матричная форма записи системы (8):

Вернемся к нелинейной модели ЭЭС. Для этого перенесем составляющую токов базы системы (4) в левую часть, изменив при этом диапазон [math]i=1 \ldots (N-1)[/math] . Получаем:

Добавим, что [math]\dot = P + j Q.[/math] (12)

Подставляем (11) в выражение (10), получаем следующее:

Подставляем (1), (3), (12) в (13), получаем:

[math]\displaystyle \begin \sum_^ \left( g_ + j b_ \right) \left( U_‘ + j U_» \right) = \frac< P_i - j Q_i >< U_i' - j U_i'' >, i = 1 \ldots (N-1)\end.[/math]

Раскрываем скобки, домножаем правую часть на сопряженное и группируем относительно [math]j[/math] :

Вынесем [math]j[/math] за знак суммы в левой части, а в правой части разобьем дробное выражение на две составляющие относительно [math]j[/math] , получим:

Преобразуем систему (14) к виду, аналогичному системе (8), и получаем нелинейную систему УУН для сети переменного тока в прямоугольных координатах в форме баланса токов:

Выведем систему нелинейных УУН для сети переменного тока в прямоугольных координатах в форме баланса мощностей. Для этого домножим систему (13) на [math]\hat[/math] , получаем:

[math]\displaystyle \begin\left(U_i’-jU_i»\right)\sum_^\left(g_+jb_\right)\left(U_‘+jU_»\right)=P_i-jQ_i\end, i=1 \ldots (N-1).[/math]

Вносим сопряженный комплекс напряжения под знак суммы и группируем относительно [math]j[/math] , имеем:

Преобразуем систему (17) к виду, аналогичному системе (15), и получаем нелинейную систему УУН для сети переменного тока в прямоугольных координатах в форме баланса мощностей:

В полярной системе координат

Комплексное число можно представить в алгебраической, показательной и тригонометрической формах:

[math]\displaystyle \dot=U_k’+jU_k» = V_k \cdot e^ = V_k \big(\cos(δ_k)+j \sin(δ_k)\big).[/math]

Для того, чтобы вывести УУН в форме баланса мощностей в полярной системе координат, необходимо в систему (16) подставить показательную запись комплексного числа [math]\dot[/math] . Выполнив это, получим:

[math]\displaystyle \begin V_i e^ <-j δ_i>\sum_ \limits^ (g_ + j b_) \cdot V_k \cdot e^ = P_i — j Q_i \end, i= \overline< 1 \ldots (N-1) >.[/math]

Переносим экспоненты в одну сторону:

[math]\displaystyle \begin V_i\sum_\limits^V_k(g_+jb_) \cdot e^ \cdot e^<-jδ_i>=P_i-jQ_i\end, i= \overline< 1 \ldots (N-1) >.[/math]

Используя свойство степеней, выполним преобразования:

[math]\displaystyle \begin V_i\sum_\limits^ V_k (g_+jb_) \cdot e^ = P_i — jQ_i\end, i= \overline< 1 \ldots (N-1) >.[/math]

Переходим к тригонометрической форме:

[math]\displaystyle \begin V_i\sum_\limits^ V_k \bigg( \big(g_ + jb_ \big) \big( \cos(δ_k-δ_i) + j \cdot \sin(δ_k-δ_i) \big) \bigg) = P_i-jQ_i \end, i= \overline< 1 \ldots (N-1) >.[/math]

Группируем относительно [math]j[/math] :

Преобразуем систему (19) к виду, аналогичному системе (15), и получаем нелинейную систему УУН для сети переменного тока в полярных координатах в форме баланса мощностей:

Методы решения

Основные методы решения системы уравнений узловых напряжений:

1. Метод Гаусса-Зейделя — это один из самых первых разработанных методов. Обычно показывает более медленную сходимость по сравнению с другими итерационными методами. Основными особенности — это малое использование памяти и не требуется матричная алгебра.
2. Метод Якоби.
3. Метод Z-матриц.
4. Метод Ньютона-Рафсона — один из самых популярных методов решения, основанный на разложении в ряд Тейлора.
5. Метод голоморфного встраивания — прямой метод расчёта на основе комплексного анализа.

Уравнения установившегося режима электрической сети

Установившимся режимом работы электрической сети при постоянных источниках тока и напряжения называется такое её состояние, при котором ток в любой ветви и напряжение в любом узле остаются относительно неизменны-ми в течение сколь угодно длительного времени.

Рассмотрим узел электрической сети, в котором соединены несколько ветвей. В качестве ветвей могут быть участки ЛЭП, трансформаторы, батареи статических конденсаторов (БСК), синхронные компенсаторы (СК) и другие элементы электрической сети.

1,2,3,…,j – номера узлов, имеющих электрическую связь с рассматриваемым

;

y_i0 – проводимость i — го узла, включающая проводимости (поперечные)

элементов, установленных в i – м узле (БСК, СК, реакторы, и другие

элементы), половины поперечных проводимостей линий, подключен-

ных в i – м узле, поперечные проводимости трансформаторов (если

они примыкают к этому узлу узлом начала схемы замещения).

.

— токи в ветвях, примыкающих и к рассматриваемому узлу. В зависимости от направления тока устанавливается знак » + » или » — » , если ток , то противоположный ему ток

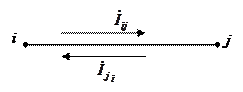
Расчетное направление тока или мощности может не совпадать с реальным.

В этом случае они будут отличаться знаками.

В соответствии с I — законом Кирхгофа в узле i должен соблюдаться баланс токов, то есть сумма токов в ветвях, присоединенных к узлу (с учетом направ-лений токов ) должна быть равна инъекции тока в узле:

(1)

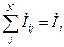
N – количество узлов непосредственно связанных с i – м узлом.

Инъекцию тока в узле Іi можно определить:

(2)

Левая часть уравнения выражения (1):

(3)

Объединим выражения (2) и (3), и запишем формулу (1):

(4)

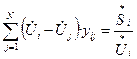
Умножим обе части уравнения (4) на :

(5)

Рассмотрим левую часть уравнения (4). Запишем баланс токов в i – м узле в развернутом виде:

(6)

(7)

Сгруппируем элементы в левой части:

(8)

y_ij – взаимная проводимость узлов i и j. Равна продольной проводимости участка i – j : y_ij = 1 / Z_ij .

— собственная проводимость узла. Равна сумме проводи-мостей всех участков, присоединенных к i – му узлу:

Во вторых скобках – сумма произведений напряжений узлов, соединенных с i – м, на их взаимные проводимости.

Запишем уравнение (8) с учетом принятых обозначений:

Это уравнение установившегося режи-ма в форме баланса токов.

(9) Оно описывает режим i — го узла и

баланс токов в нём.

Неизвестным являются напряжения узлов: — напряжение рассматрива-емого узла, — напряжение в узлах, непосредственно связанных с i – м узлом.

Заданные величины: инъекция тока . Известными являются: собственная проводимость узла , взаимная проводимость . Уравнение (9) линейно относительно неизвестных напряжений в узлах.

Подставим в правую часть формулы (9) формулу (2):

(10)

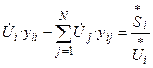
Умножим обе части уравнения (10) на :

.

Получаем уравнение установившегося режима в форме баланса мощности:

Описывает баланс мощностей в i – м узле.

— сопряженный комплекс мощности, заданной в i – м узле.

Неизвестные величины: напряжения в узлах .

Известные величины: .

Уравнение (11) — нелинейное относительно неизвестных напряжений.

1. Уравнения (9) и (11) – уравнения с комплексными неизвестными и

комплексными неизвестными. Содержат параметры, характеризую-

щие схему сети (проводимости y_ii и y_ij) и её режим ( напряжения U_i

2. Неизвестными величинами в них являются напряжения узлов U_i и U_j ;

3. Известные величины в них – собственная и взаимные проводимости

узлов. Заданные величины – ток и мощность в узле;

4. Уравнения записаны для одного узла электрической сети. Для схемы,

состоящей из N узлов, потребуется записать систему из N таких

Лекция 8

В практических расчетах комплексные уравнения (9) и (11) часто исполь-зуются в преобразованном виде. Комплексные величины в их составе пред-ставляются в виде действительных и мнимых составляющих. В результате, комплексное уравнение распадается на два действительных уравнения.

Преобразуем уравнение (11), представив неизвестные напряжения (комп-лексные величины) U_i ,U_j в прямоугольных координатах:

Проводимости тоже представим в виде составляющих:

(12)

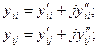
Мощность: ;

Подставим эти значения в (11):

Выполняем преобразование: раскрываем скобки, группируем, разделяем действительную и мнимую части уравнения. Получаем два действительных

уравнения установившегося режима в форме баланса мощностей, записанных в прямоугольных координатах:

(13)

Неизвестные величины в них — составляющие напряжений U_i ’ , U_i ” , U_j ’ , U_j ” .

Уравнение (13) описывает баланс активной и реактивной мощности в одном i – м узле сети. Для сети, состоящей из n узлов нужно записать 2n таких урав-нений. Неизвестными являются составляющие напряжения .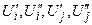

Представим уравнение (11) в полярных координатах. Для этого комплексы неизвестных напряжений запишем в соответствии с формулой Эйлера:

.

Здесь U_i – модуль, 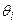— фаза напряжения .

(14)

Подставим (14) в (11) учетом того, что

(15)

Преобразуем уравнение (15): раскрываем скобки, группируем, разделя-ем действительные и мнимые части, меняем местами

(16)

Это уравнение установившегося режима в форме баланса мощности,

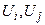
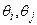
записанное в полярных координатах. Неизвестные величины в нём — модули напряжений и фазы напряжений .

Это два действительных уравнения, записанные для одного i-го узла схемы. Определяют баланс активной и реактивной мощности в нем.

Существуют и другие формы записи уравнений установившегося режима.

Пример:

Составить уравнения в форме баланса токов для каждого из узлов сети

Составим уравнение для первого узла.

— собственная проводимость 1 – го узла.

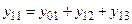
Для узла 0: i=0; j=1; n=1;

Для узла 2: i=2; j=1,3; n=2;

Для узла 3: i=3; j=1,2; n=2;

Уравнения в форме баланса мощностей можно получить, если умножить каждое из полученных уравнений на сопряженный комплекс соответствующе-го напряжения.

Запишем уравнение для 1 – го узла в прямоугольных координатах:

Для узлов 2 и 3 уравнения в прямоугольных координатах записать самостоятельно.

Уравнения для 1-го узла в полярных координатах: