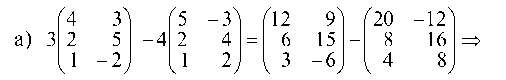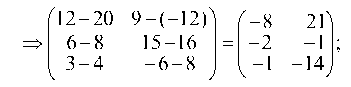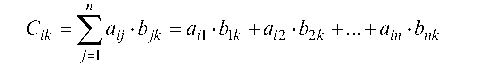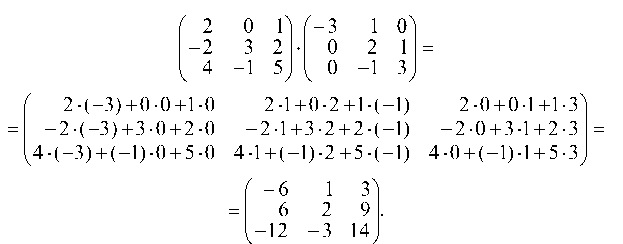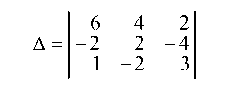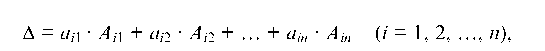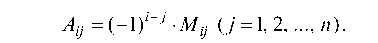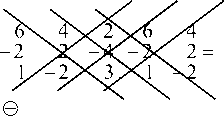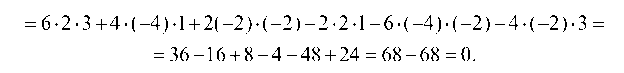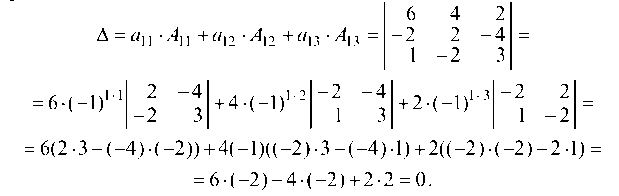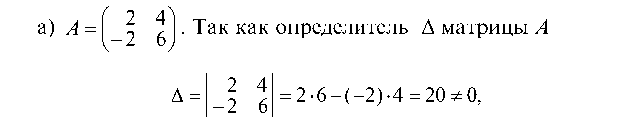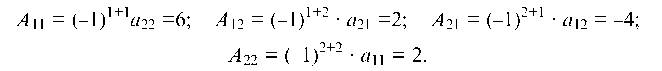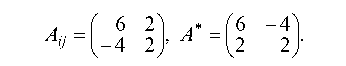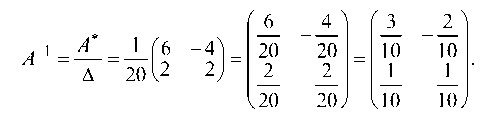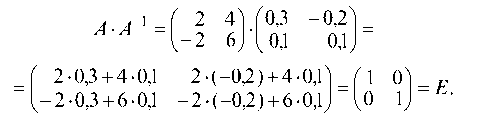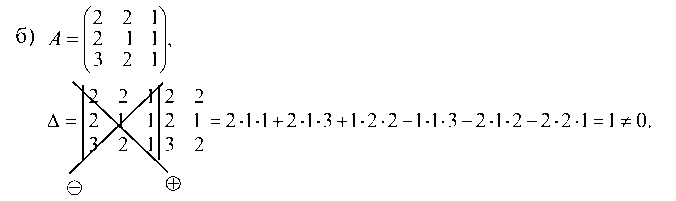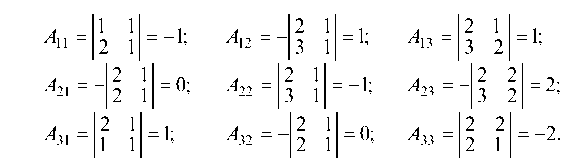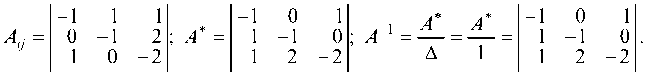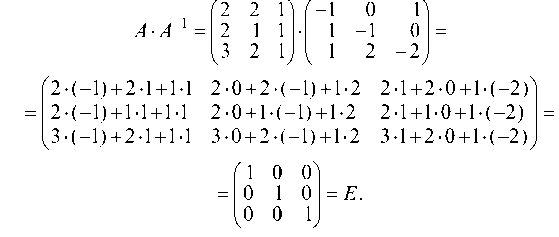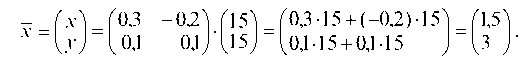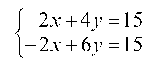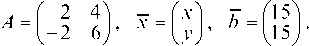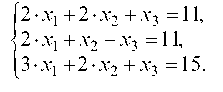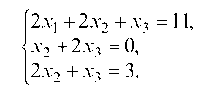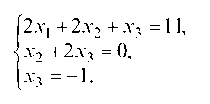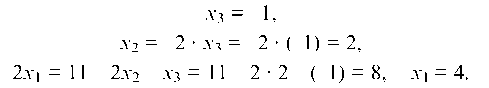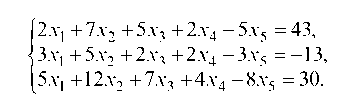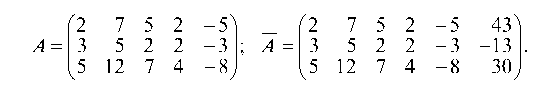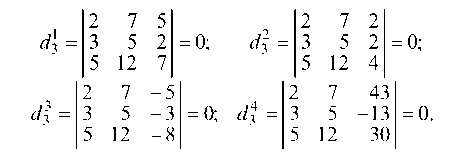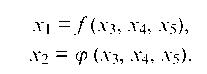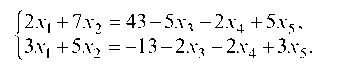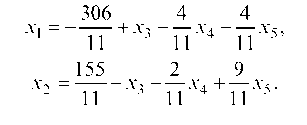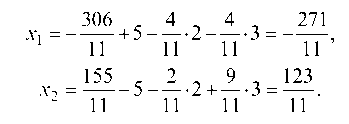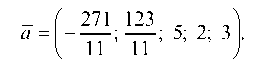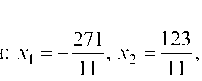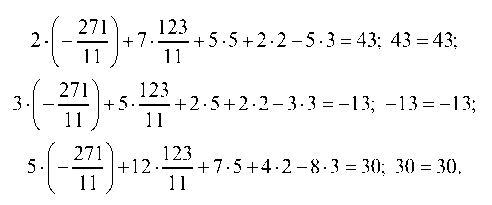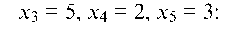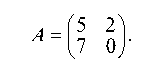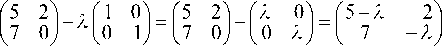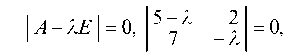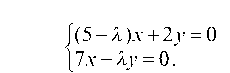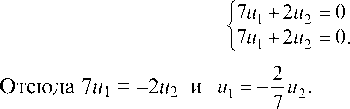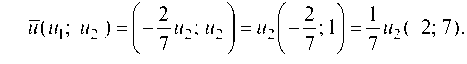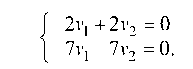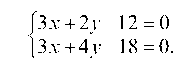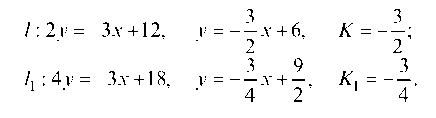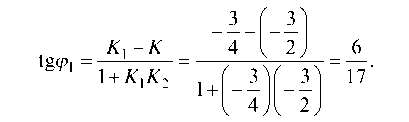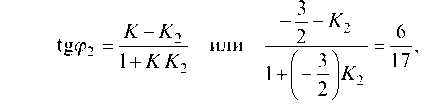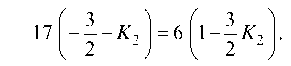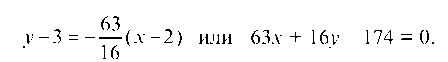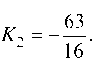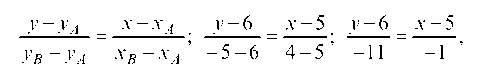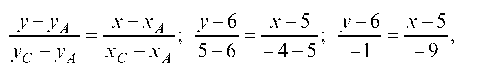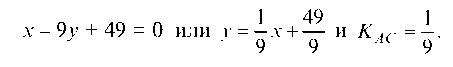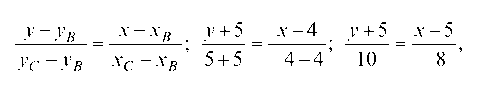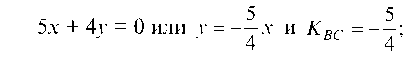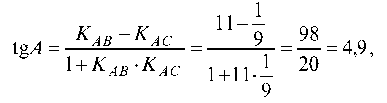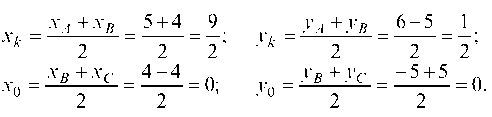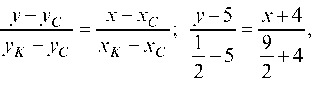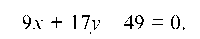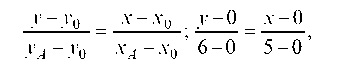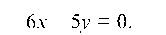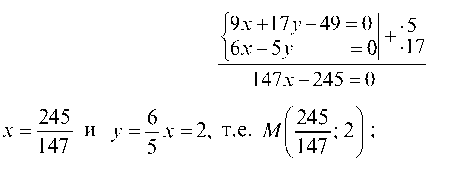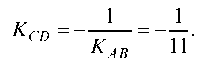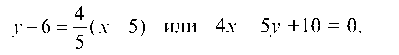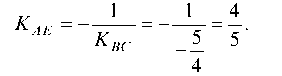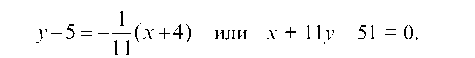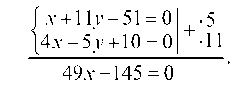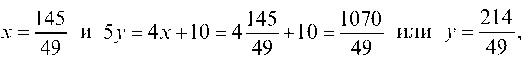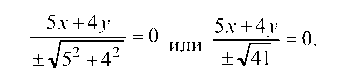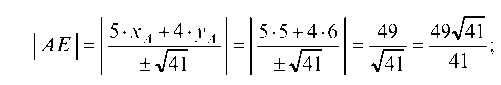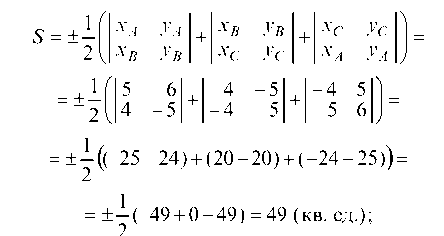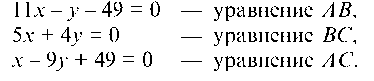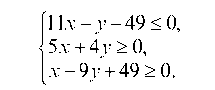А уравнение отраженного луча в среде 1

Законы отражения света

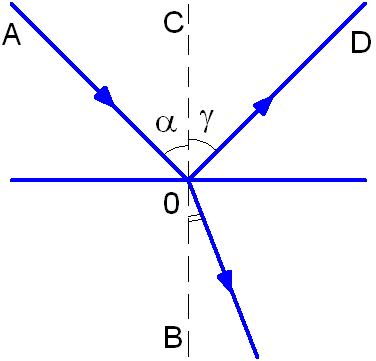
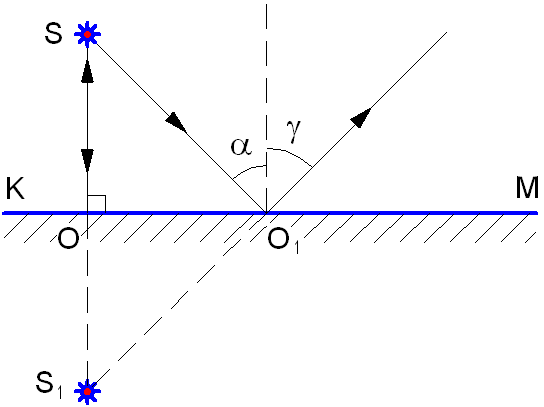
На границе раздела двух различных сред, если эта граница раздела значительно превышает длину волны, происходит изменение направления распространения света: часть световой энергии возвращается в первую среду, то есть отражается, а часть проникает во вторую среду и при этом преломляется. Луч АО носит название падающий луч, а луч OD – отраженный луч (см. рис. 1.3). Взаимное расположение этих лучей определяют законы отражения и преломления света.

Рис. 1.3. Отражение и преломление света.

Угол α между падающим лучом и перпендикуляром к границе раздела, восстановленным к поверхности в точке падения луча, носит название угол падения.

Угол γ между отражённым лучом и тем же перпендикуляром, носит название угол отражения.

Каждая среда в определённой степени (то есть по своему) отражает и поглощает световое излучение. Величина, которая характеризует отражательную способность поверхности вещества, называется коэффициент отражения. Коэффициент отражения показывает, какую часть принесённой излучением на поверхность тела энергии составляет энергия, унесённая от этой поверхности отражённым излучением. Этот коэффициент зависит от многих причин, например, от состава излучения и от угла падения. Свет полностью отражается от тонкой плёнки серебра или жидкой ртути, нанесённой на лист стекла.

Законы отражения света

Законы отражения света были найдены экспериментально ещё в 3 веке до нашей эры древнегреческим учёным Евклидом. Также эти законы могут быть получены как следствие принципа Гюйгенса, согласно которому каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Волновая поверхность (фронт волны) в следующий момент представляет собой касательную поверхность ко всем вторичным волнам. Принцип Гюйгенса является чисто геометрическим.

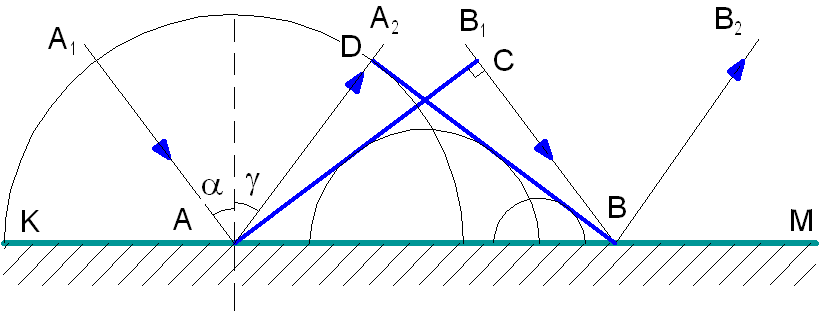
На гладкую отражательную поверхность КМ (рис. 1.4) падает плоская волна, то есть волна, волновые поверхности которой представляют собой полоски.

Рис. 1.4. Построение Гюйгенса.

А₁А и В₁В – лучи падающей волны, АС – волновая поверхность этой волны (или фронт волны).

Пока фронт волны из точки С переместится за время t в точку В, из точки А распространится вторичная волна по полусфере на расстояние AD = CB, так как AD = vt и CB = vt, где v – скорость распространения волны.

Волновая поверхность отражённой волны – это прямая BD, касательная к полусферам. Дальше волновая поверхность будет двигаться параллельно самой себе по направлению отражённых лучей АА₂ и ВВ₂.

Прямоугольные треугольники ΔАСВ и ΔADB имеют общую гипотенузу АВ и равные катеты AD = CB. Следовательно, они равны.

Углы САВ = = α и DBA = = γ равны, потому что это углы со взаимно перпендикулярными сторонами. А из равенства треугольников следует, что α = γ .

Из построения Гюйгенса также следует, что падающий и отражённый лучи лежат в одной плоскости с перпендикуляром к поверхности, восстановленным в точке падения луча.

Законы отражения справедливы при обратном направлении хода световых лучей. В следствие обратимости хода световых лучей имеем, что луч, распространяющийся по пути отражённого, отражается по пути падающего.

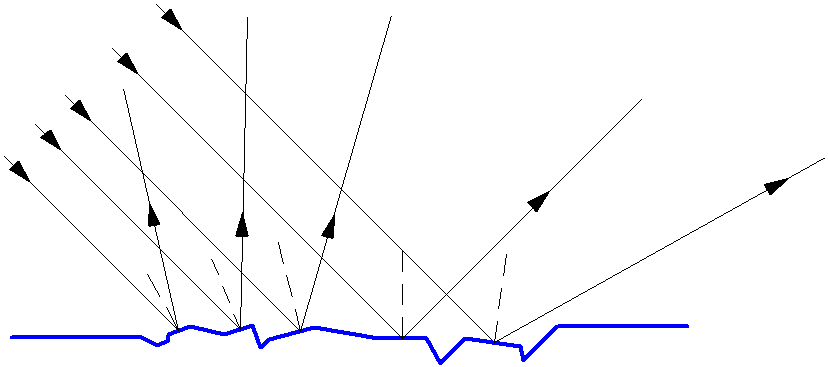
Большинство тел лишь отражают падающее на них излучение, не являясь при этом источником света. Освещённые предметы видны со всех сторон, так как от их поверхности свет отражается в разных направлениях, рассеиваясь. Это явление называется диффузное отражение или рассеянное отражение. Диффузное отражение света (рис. 1.5) происходит от всех шероховатых поверхностей. Для определения хода отражённого луча такой поверхности в точке падения луча проводится плоскость, касательная к поверхности, и по отношению к этой плоскости строятся углы падения и отражения.

Рис. 1.5. Диффузное отражение света.

Например, 85% белого света отражается от поверхности снега, 75% — от белой бумаги, 0,5% — от чёрного бархата. Диффузное отражение света не вызывает неприятных ощущений в глазу человека, в отличие от зеркального.

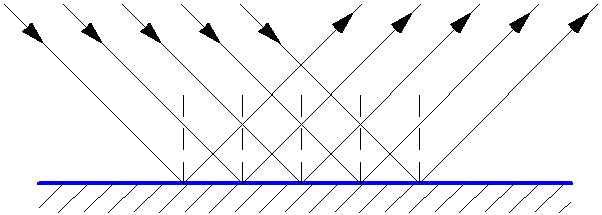
Зеркальное отражение света – это когда падающие на гладкую поверхность под определённым углом лучи света отражаются преимущественно в одном направлении (рис. 1.6). Отражающая поверхность в этом случае называется зеркало (или зеркальная поверхность). Зеркальные поверхности можно считать оптически гладкими, если размеры неровностей и неоднородностей на них не превышают длины световой волны (меньше 1 мкм). Для таких поверхностей выполняется закон отражения света.

Рис. 1.6. Зеркальное отражение света.

Плоское зеркало – это зеркало, отражающая поверхность которого представляет собой плоскость. Плоское зеркало даёт возможность видеть предметы, находящиеся перед ним, причём эти предметы кажутся расположенными за зеркальной плоскостью. В геометрической оптике каждая точка источника света S считается центром расходящегося пучка лучей (рис. 1.7). Такой пучок лучей называется гомоцентрическим. Изображением точки S в оптическом устройстве называется центр S’ гомоцентрического отражённого и преломлённого пучка лучей в различных средах. Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь от него, падает в глаз наблюдателя, то в зеркале видны изображения этих тел.

Рис. 1.7. Изображение, возникающее с помощью плоского зеркала.

Изображение S’ называется действительным, если в точке S’ пересекаются сами отражённые (преломлённые) лучи пучка. Изображение S’ называется мнимым, если в ней пересекаются не сами отражённые (преломлённые) лучи, а их продолжения. Световая энергия в эту точку не поступает. На рис. 1.7 представлено изображение светящейся точки S, возникающее с помощью плоского зеркала.

Луч SO падает на зеркало КМ под углом 0°, следовательно, угол отражения равен 0°, и данный луч после отражения идёт по пути OS. Из всего множества попадающих из точки S лучей на плоское зеркало выделим луч SO₁.

Луч SO₁ падает на зеркало под углом α и отражается под углом γ ( α = γ ). Если продолжить отражённые лучи за зеркало, то они сойдутся в точке S₁, которая является мнимым изображением точки S в плоском зеркале. Таким образом, человеку кажется, что лучи выходят из точки S₁, хотя на самом деле лучей, выходящих их этой точки и попадающих в глаз, не существует. Изображение точки S₁расположено симметрично самой светящейся точке S относительно зеркала КМ. Докажем это.

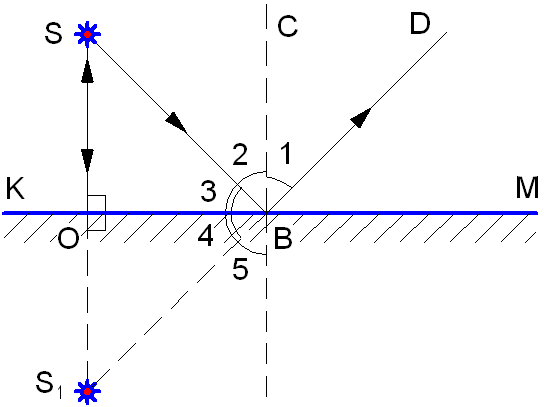
Луч SB, падающий на зеркало под углом 2 (рис. 1.8), согласно закону отражения света отражается под углом 1 = 2.

Рис. 1.8. Отражение от плоского зеркала.

Из рис. 1.8 видно, что углы 1 и 5 равны – как вертикальные. Суммы углов 2 + 3 = 5 + 4 = 90°. Следовательно, углы 3 = 4 и 2 = 5.

Прямоугольные треугольники ΔSOB и ΔS₁OB имеют общий катет ОВ и равные острые углы 3 и 4, следовательно, эти треугольники равны по стороне и двум прилежащим к катету углам. Это означает, что SO = OS₁, то есть точка S₁ расположена симметрично точке S относительно зеркала.

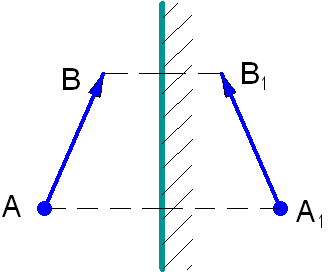
Для того чтобы найти изображение предмета АВ в плоском зеркале, достаточно опустить перпендикуляры из крайних точек предмета на зеркало и, продолжив их за пределы зеркала, отложить за ним расстояние, равное расстоянию от зеркала до крайней точки предмета (рис. 1.9). Это изображение будет мнимым и в натуральную величину. Размеры и взаимное расположение предметов сохраняются, но при этом в зеркале левая и правая стороны у изображения меняются местами по сравнению с самим предметом. Параллельность падающих на плоское зеркало световых лучей после отражения также не нарушается.

Рис. 1.9. Изображение предмета в плоском зеркале.

В технике часто применяют зеркала со сложной кривой отражающей поверхностью, например, сферические зеркала. Сферическое зеркало – это поверхность тела, имеющая форму сферического сегмента и зеркально отражающая свет. Параллельность лучей при отражении от таких поверхностей нарушается. Зеркало называют вогнутым, если лучи отражаются от внутренней поверхности сферического сегмента. Параллельные световые лучи после отражения от такой поверхности собираются в одну точку, поэтому вогнутое зеркало называют собирающим. Если лучи отражаются от наружной поверхности зеркала, то оно будет выпуклым. Параллельные световые лучи рассеиваются в разные стороны, поэтому выпуклое зеркало называют рассеивающим.

Решение типовых задач контрольной работы по разделам 1 и 2

Тема «Функции нескольких переменных» будет рассмотрена после определенного интеграла.

1. ЛИНЕЙНАЯ АЛГЕБРА

1.1. Действия с матрицами

1.1.1. Выполнить действия

Сначала умножаем матрицу на число, а затем вычитаем из одной матрицы другую

б) нужно перемножить две матрицы: С = AS. Это возможно в случае, если число столбцов матрицы А равно числу строк матрицы S. Элемент Cjk матрицы С имеет вид:

(г = 1, 2, . и; к = 1, 2, . и), т. е. элемент матрицы С, стоящей в г-й строке и к-м столбце, равен сумме произведений соответственных элементов г-й строки матрицы А и к-го столбца матрицы S.

Справа от определителя приписываются два первых столбца, берутся со знаком «+» три произведения элементов, стоящих на главной диагонали и двух диагоналях ей параллельной и со знаком минус три произведения элементов, стоящих на побочной диагонали и двух диагоналях ей параллельной;

б) разложением по строке.

Определитель D равен сумме произведений всех элементов произвольной его строки на их алгебраические дополнения

где Aj — алгебраическое дополнение элемента определителя Яу, равное

1.2.1. Убедимся, что определитель D равен нулю

а) по определению (одной из схем):

Здесь Mj — минор элемента Яу, т. е. определитель (n — 1)-го порядка, получающийся после вычеркивания из определителя n-го порядка i-й строки и у-го столбца.

Вычисляем определитель D разложением по элементам первой строки

1.3. Обратная матрица

1.3.1. Найти обратную матрицу к матрице А и проверить выполнение равенства А ¦ A1 = £:

то матрица А является невырожденной и для нее существует об-

ратная матрица А 1.

Находим алгебраические дополнения для определителя Д:

Составляем матрицу из этих алгебраических дополнений и транспонируя ее, получаем присоединенную матрицу (А*):

Вычисляем обратную матрицу А

Так как А ¦ А 1 = то обратная матрица найдена правильно;

Находим алгебраические дополнения

Отсюда: х = 1,5; у = 3.

1.4.1. Записать систему в матричном виде Ах = b :

и решить ее средствами матричного исчисления.

Решение этой системы через обратную матрицу А 1 имеет вид

В пункте 1.3.1: а) была найдена обратная матрица А 1, тогда

Можно сделать проверку, т. е. подставить найденные значения х и у в исходную систему уравнений.

1.4.2. Решить систему методом исключения переменных (методом Гаусса):

Выберем в качестве первого ведущего уравнения — первое уравнение системы и оно в дальнейшем остается без изменения, а в качестве первого ведущего неизвестного — хь

Исключаем неизвестную х1 из второго и третьего уравнений системы с помощью первого уравнения. Для этого из 1-го уравнения вычитаем второе, получим х2 + 2х3 = 0, затем 1-ое уравнение умножаем на 3, а 3-е уравнение — на 2 и вычитаем из одного другое, получим 2х2 + х3 = 3.

Неизвестная х1 исключена. Первый шаг закончен. Теперь второе уравнение берется за ведущее и оно в дальнейшем не изменяется, а за ведущую неизвестную принимается х2. Исключаем из 3-го уравнения х2, для этого 2-ое уравнение умножаем на 2 и вычитаем из него 3-е уравнение системы, получаем 3х3 = -3.

Прямой ход метода Гаусса закончен. Обратным ходом получаем:

Итак, х1 = 4, х2 = 2, х3 = -1.

1.4.3. Дана система

Рассмотрим минор 2-го порядка

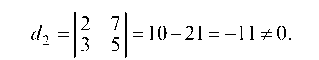
Так как миноры d^, и d| равны нулю, то ранг системы

равен двум, а так как минор = 0, то и ранг расширенной матрицы равен двум. Равенство рангов расширенной матрицы и матрицы системы на основании теоремы Кронекера—Капелли говорит о том, что система алгебраических уравнений совместна, т. е. имеет решение.

2. Найти общее решение системы в виде

Так как число неизвестных пять, а ранг матрицы равен двум, то разность между ними, равная трем (n — r = 5 — 2 = 3), говорит

о том, что три неизвестных будут свободными, пусть это будут x3, x4, x5.

Берем первые два уравнения системы и записываем их относительно x1 и x2 (коэффициенты при этих неизвестных составляют минор 2-го порядка отличный от нуля), а неизвестные x3, x4, x5 переносим в правую часть:

Имеем систему двух уравнений с двумя неизвестными x1 и x2. Умножая первое уравнение на 5, а второе на 7 и вычитая одно из другого, найдем x1 и подставляя его в 1-ое уравнение, после преобразований получим выражение для x2:

3. Найти частное решение системы a = (х1, х2, х3, х4, х5), положив х3 = 5, х4 = 2, х5 = 3 и проверить систему.

Находим х1 и х2:

Следовательно, частное решение имеет вид:

Подставляем в исходную систему значенш

Выполнение тождества для всех уравнений системы говорит о том, что вектор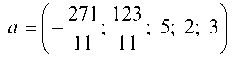Является частным реше

нием исходной системы уравнений.

1.5. Собственные числа и собственные векторы

1.5.1. Найти собственные числа и соответствующие им собственные векторы для матрицы

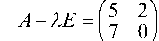
отсюда (5 — 1) ¦ (-1) — 2 ¦ 7 = 0, или I2 — 51 — 14 = 0. Корни этого уравнения 1 = -2 и 12 = 7 и являются собственными числами.

Для отыскания собственных векторов используем систему уравнений

Полагая 1 = 11 = -2, получаем систему уравнений для первого собственного вектора U(M1, M2):

Следовательно, первым собственным вектором, определяющим первое собственное направление, является

Меняя M2, будем получать различные векторы, лежащие на одной прямой (коллинеарные). Все они — собственные.

Полагая 1 = 12 = 7, получаем систему уравнений для отыскания координат второго собственного вектора V (V1; v2):

Отсюда v1 = v2 — общее решение (v2 — свободная, v1 — базисная переменная).

Второй собственный вектор V(V1; v2) = (v2; v2) = V2 (1; 1) определяет второе собственное направление.

2.1. Прямая линия на плоскости

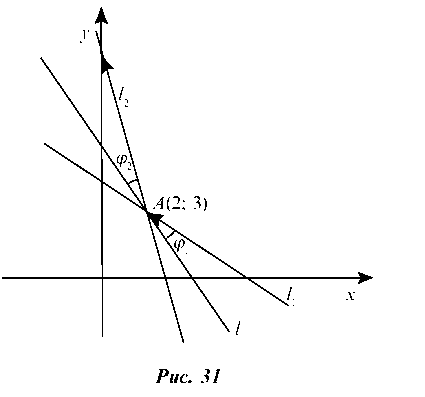
2.1.1. На прямую /: 3x + 2y — 12 = 0, которая способна отражать лучи, падает луч, заданный уравнением I1: 3x + 4y — 18 = 0. Составить уравнение отраженного луча.

Решение. Так как угол падения луча равен углу отражения луча, то Zj = Z j2, т. е. tg j1 = tg j2 (рис. 31).

Уравнение отраженного луча — прямой /2 — ищем в виде: y — yA = k2(x — xa).

Для нахождения координат точки А решим систему уравнений:

Вычитая, найдем: -2у + 6 = 0, у = 3 и 3x = 12 -2у = 12 — 2 ¦ 3 = 6, x = 2, т. е. xA = 2 и yA = 3.

Найдем угловые коэффициенты прямых / и /1:

Запишем тангенс угла между прямыми / и /1:

Для нахождения углового коэффициента прямой /2 запишем тангенс угла между прямыми / и /2 и учтем, что tg Р1 = tg (pi-

Отсюда Т огда искомое уравнение отраженного луча

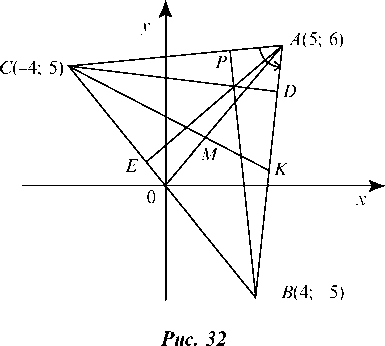
2.1.2. Дан треугольник АВС с вершинами А(5; 6), B(4; -5), C(-4; 5) (рис. 32).

Найдем уравнения всех сторон треугольника и их угловые коэффициенты.

Уравнение прямой AS:

отсюда 11 ¦ х — у — 49 = 0 или у = 11х — 49 и угловой коэффициент прямой AS равен: Kab = 11.

Уравнение прямой AC:

Уравнение прямой SC: отсюда

а) вычислим величину внутреннего угла А треугольника:

отсюда ZA = 78°27’55» = 1,37 (с точностью до 0,01) радиан;

б) найдем точку M пересечения медиан.

Определяем координаты точек K и O, делящих стороны AS и SC попалам:

Уравнение медианы CK:

отсюда

Уравнение медианы AO:

отсюда

Решая систему уравнений, описывающих медианы CK и AO, найдем координаты точки M:

в) находим точку Р пересечения высот CD и AE.

Уравнение высоты CD ищем в виде: y — yC = KCD(x — xC) и так как прямая CD L прямой AS, то

Уравнение высоты AE берем в виде: y — yA = KAE(x — xA) и так как прямая AE L прямой SC, то

г) определяем длину высоты треугольника А£, опущенной из вершины А на сторону SC, для чего запишем нормальное уравнение прямой SC:

е) находим систему линейных неравенств, определяющих внутреннюю область треугольника ASC вместе с границами.

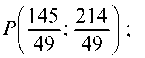
Тогда длина высоты А£ равна:

д) площадь треугольника найдем по формуле:

Имеем:

Берем любую точку, лежащую внутри треугольника ASC, например, точку (1; 1) и подставляем ее координаты в левую часть уравнений сторон: 11 ¦ 1 — 1 — 49 = -39 0;

1 — 9 ¦ 1 + 49 = 41 > 0, следовательно, система неравенств имеет вид:

Геометрическая оптика. Общие свойства лучей

Геометрическая оптика. общие свойства лучей

В рамках электромагнитной теории света его распространение представляет собой волновой процесс. С помощью волновой теории мы можем решать задачи о распространении света, как в однородной среде, так и через любую оптическую систему, т. е. совокупность различных сред, ограниченных теми или иными поверхностями или диафрагмами. Однако в очень многих областях, имеющих важное практическое значение, в частности, при решении вопросов формирования световых пучков (светотехника), образования изображения (оптотехника), решение можно получить гораздо более простым путем, с помощью представлений геометрической оптики. Интуитивно ясный и применяемый обычно без дополнительных объяснений метод геометрической оптики оперирует понятием отдельных световых лучей, поведение которых в окружающих средах было установлено экспериментально, как уже известно из исторического введения. Построения с помощью световых лучей достаточно формальны, удобны в использованиии и в большом числе случаев вполне адекватно описывают формирование даже самых сложных оптических изображений.

Понятие светового луча можно получить из рассмотрения реального светового пучка в однородной среде, из которого при помощи одной или нескольких диафрагм с отверстиями выделяется узкий параллельный пучок. Чем меньше диаметр этих отверстий, тем уже выделяемый пучок, и в пределе, переходя к отверстиям сколь угодно малым, можно, казалось бы, получить световой луч как прямую линию. Однако подобный процесс выделения сколь угодно узкого пучка (луча) невозможен вследствие явления дифракции. Неизбежное угловое расширение реального светового пучка с длиной волны l, пропущенного через диафрагму диаметра D, определяется углом дифракции j » l ¤ D (см. Оптика ч. 2, раздел “Дифракция на круглой апертуре”). Таким образом, световой луч есть абстрактное математическое понятие, а не физический образ, и приближение геометрической оптики на самом деле требует некоторого обоснования и определения границ его применимости.

Только в предельном случае, когда l ® 0, подобное расширение не имело бы места, и можно было бы говорить о луче как о геометрической линии, направление которой определяет направление распространения световой энергии. Таким образом, световой луч есть абстрактное математическое понятие, а не физический образ, и геометрическая оптика есть лишь предельный случай волновой оптики, соответствующий исчезающе малой длине световой волны.

Соотношение j » l ¤ D показывает, что угловое отклонение, нарушающее прямолинейность распространения света в однородной среде, может быть весьма мало, если размеры отверстия или экрана велики по сравнению с длиной волны l. Поэтому в реальной оптике, где l — конечная величина, отступления от законов геометрической оптики должны быть тем меньше, чем больше размеры диафрагмы.

Таким образом, при пользовании законами геометрической (лучевой) оптики нельзя забывать, что они — лишь первое приближение к действительности и что без дифракционных явлений не обходится ни один случай распространения света. Необходимо, следовательно, понимать волновой (дифракционный) смысл этих геометрических построений. Из этого ясно, что законы геометрической оптики имеют ограниченное применение, и надо уметь ориентироваться, при каких условиях применение этих законов допустимо и будет находиться в достаточном соответствии с экспериментом. Оказывается, что даже в практической оптике наиболее тонкие вопросы (например, вопрос о разрешающей силе оптических инструментов) решаются только в рамках теории дифракции.

1.2 Уравнение эйконала

Рассмотрим монохроматическую световую волну с длиной волны в вакууме l0, распространяющуюся в немагнитной (m = 1) среде с показателем преломления . Поле этой волны должно удовлетворять уравнению Гельмгольца

, (1.1)

где – волновой вектор, обратный длине волны.

Будем искать решение этого уравнения в виде

, (1.2)

где L(r) – вещественная скалярная функция координат, имеющая размерность длины и называемая оптическим путем или эйконалом (от греческого eikon – путь). Нетрудно видеть, что равенство L = const определяет поверхность постоянной фазы, т. е. геометрический волновой фронт.

Подставим выражение (1.2) в (1.1) и перейдем к пределу геометрической оптики l®0 (k0®¥), оставив только слагаемые с k02.Тогда получаем:

, или . (1.3)

Уравнение (1.3) называется уравнением эйконала и является основным уравнением, описывающим поведение света в приближении геометрической оптики. Отметим, что при его выводе мы пренебрегли многочисленными слагаемыми, получающимися при дифференцировании уравнения волны (1.2). Отсюда следует, что приближение геометрической оптики справедливо, если изменения амплитуды e на расстоянии порядка длины волны малы по сравнению с самой амплитудой. Это условие, очевидно, нарушается на границе геометрической тени, так как. там интенсивность света, а значит и напряженность поля, меняется скачком. Действительно, именно на границе тени особенно ярко проявляют себя дифракционные эффекты, обусловленные волновой природой света. Нельзя также ожидать, что геометрическая оптика даст правильное описание полей вблизи точек, где имеется резкий максимум интенсивности, например, в окрестности формируемого линзой оптического изображения точечного источника, образующегося в линзе.

Уравнение эйконала можно также записать в векторной форме. Введем единичный вектор s, совпадающий по направлению с вектором grad L, тогда

. (1.4)

Из векторного анализа известно, что вектор градиента всегда ортогонален поверхности уровня функции, т. е. поверхности, на которой функция постоянна. В данном случае поверхность уровня для эйконала представляет собой волновой фронт, следовательно s – орт нормали к волновому фронту. Исходя их уравнений Максвелла можно показать, что направление вектора Пойнтинга, определяющего перенос энергии света, совпадает с вектором s. Таким образом, линии векто­ра s представляют собой геометрические световые лучи. Рис. 1.1 иллюстрирует тот факт, что семейство волновых фронтов (a, b, c) и семейство световых лучей (1, 2, 3) образуют ортогональную (в общем случае криволинейную) сеть.

1.3 Законы распространения лучей

Оптический путь

Рассмотрим два последовательных близких положения волнового фронта (рис. 1.2). Из (1.4) следует, что в силу ортогональности отрезка ds волновым поверхностям , т. е.

. (1.5)

Это означает, что расстояние между соседними волновыми фронтами увеличивается по мере уменьшения показателя преломления. Таким образом, на рис. 1.1 показатель преломления среды в левой части рисунка больше, чем в правой. Из сказанного следует, что оптическая длина пути совпадает с геометрической только в вакууме (n = 1), во всех других средах dL > ds.

Учтем, что , где dt – время прохождения лучом расстояния ds. Тогда из (1.5) следует, что оптическая длина пути между двумя точками Р1 и Р2, лежащими на одном луче, равна

, (1.6)

т. е. оптический путь между двумя точками равен скорости света в вакууме, умноженной на время прохождения лучом расстояния между этими точками.

Уравнение светового луча в неоднородной среде

Обсудим более детально характер искривления лучей в неоднородной среде. Будем рассматривать радиус-вектор r точки P, лежащей на луче, как функцию длины дуги луча s (рис. 1.3). Тогда и уравнение эйконала запишется в виде . Продифференцируем это уравнение по длине дуги s, учитывая, что , получаем

. (1.6)

Поскольку вторая производная от радиус-вектора характеризует кривизну луча, из (1.6) следует, что в неоднородной среде световые лучи изгибаются в сторону увеличения показателя преломления. Этот вывод согласуется с ходом лучей на рис. 1.1.

Искривлением световых лучей в неоднородной среде объясняется появление миражей. Нижние миражи (рис. 1.4а) обусловлены тем, что слои воздуха, прилегающие к нагретой поверхности песка в пустыне имеют меньшую плотность (а значит и меньший показатель преломления), в результате возникает изображение удаленных предметов, как при отражении в зеркале. К этому же типу оптической иллюзии относится известный всем автомобилистам эффект зеркальных “луж” на нагретом асфальте.

Для возникновения так называемого верхнего миража (рис. 1.4б) необходимо, чтобы показатель преломления приповерхностного слоя воздуха достаточно быстро уменьшался с высотой, что возможно, когда, например, внизу располагается холодный слой, а над ним находится слой более теплого воздуха.

Эффект атмосферной рефракции возникает из-за искривления световых лучей при наклонном прохождении верхних слоев атмосферы (рис. 1.4в). Благодаря этому Солнце остается видимым еще некоторое время после ухода под горизонт, а видимые положения небесных светил смещаются относительно истинных в сторону зенита.

Закон прямолинейного распространения света в однородных средах

Из уравнения (1.6) следует, что в однородной среде (n = const, grad n = 0) кривизна лучей равна нулю, т. е. свет распространяется прямолинейно. Этот закон может считаться прочно установленным на опыте, он встречается еще за 600 лет до нашей эры в сочинениях Фалеса Милетского. Он имеет глубокий смысл, ибо понятие о прямой линии, по-видимому, возникло из оптических наблюдений. Геометрическое понятие прямой как линии, представляющей кратчайшее расстояние между двумя точками, есть понятие о линии, по которой распространяется свет в однородной среде, образуя геометрические тени (рис. 1.5).

Закон интенсивности

Рассмотрим узкую трубку лучей, выходящих из элемента dS1 волнового фронта L = a1 и пусть dS2 – элемент, который пересекают эти лучи на другом волновом фронте L = a2 (рис. 1.6). Поскольку направление вектора Пойнтинга в каждой точке трубки совпадает с направлением луча, полная энергия, протекающая по трубке постоянна и не зависит от изменения ее сечения: W1 = W2. Тогда интенсивности I1 и I2 в двух сечениях связаны соотношением , выра­жающим закон интенсивности в геометрической оптике: произведение IdS остается постоянным вдоль трубки лучей. В частном случае, если пучок прямолинейных лучей выходит из одной точки, а волновые фронты имеют вид сферических поверхностей, интенсивность света оказывается обратно пропорциональной квадрату расстояния от источника.

Закон независимости световых пучков

Закон независимости включает в себя два положения: а) если световой пучок разбить на отдельные пучки с помощью диафрагм, то действие на экране этих выделенных пучков оказывается независимым от того, действуют ли одновременно другие пучки, или они устранены; б) распространение всякого светового пучка в среде совершенно не зависит от того, есть в ней другие пучки света или нет. Закон независимости световых пучков необходимо дополнить утверждением, определяющим совместное действие световых пучков при попадании их на освещаемую поверхность: освещенность экрана, создаваемая несколькими световыми пучками, равна сумме освещенностей, создаваемых каждым пучком в отдельности. Нарушения справедливости этого утверждения имеют место в нелинейной оптике или при интерференции света.

В первом случае интенсивность пучков столь велика, что их совместное действие меняет свойства среды и поведение пучков в зоне перекрытия отличается от поведения в других областях. Во втором случае взаимная сфазированность электромагнитных волн приводит к перераспределению интенсивности света во времени и пространстве.

Стигматические световые пучки

Пользуясь представлениями лучевой (геометрической) оптики предполагается рассматривать каждую светящуюся точку источника света как вершину расходящегося пучка лучей, называемого гомоцентрическим, т. е. имеющим общий центр. Если после отражения или преломления света на границах раздела сред этот пучок превращается в пучок, сходящийся тоже в одну точку, то и последний представляет собой гомоцентрический пучок и центр его является изображением светящейся точки. При сохранении гомоцентричности каждая точка источника дает одну точку изображения (сопряженную). Такие изображения называются точечными или стигматическими (рис. 1.7).

В силу обратимости (взаимности) световых лучей (см. ниже) изображение можно рассматривать как источник, а источник — как изображение. Поэтому при стигматическом изображении центры пучков называются сопряженными точками той оптической системы, в которой происходит преобразование расходящегося гомоцентрического пучка в сходящийся. Соответственные лучи и пучки также называются сопряженными. Если в результате отражения и преломления пучок перестает быть гомоцентрическим, то стигматичность изображения теряется, и точка уже не изображается точкой. Так как в практической оптике обычно ставится задача получения изображений, точно передающих форму источника, то важнейшим вопросом геометрической оптики является выяснение условий сохранения гомоцентричности пучков.

1.4 Принцип Ферма

Найдем величину оптического пути между двумя точками А и В, лежащими на одном луче (рис. 1.8):

.

Этот интеграл, равный разности значений эйконала в точках В и А и, следовательно, не зависящий от пути интегрирования, называется интегральным инвариантом Лагранжа. Но , поэтому

. Знак равенства имеет место только в том случае, когда направления векторов s и dr совпадают в каждой точке траектории, т. е. когда она представляет собой реальный световой луч (АСВ на рис. 1.8). Для любой другой траектории, соединяющей точки А и В (например, ADB) оптическая длина пути оказывается больше, чем для реального луча.

Обобщением вышеприведенных рассуждений является принцип Ферма: свет распространяется по такой траектории, оптическая длина которой (а значит и время распространения) имеет экстремальное значение (минимальное, максимальное или стационарное) в некоторой регулярной окрестности светового луча. Под регулярной окрестностью понимается область, которую можно заполнить световыми лучами так, что через каждую точку будет проходить единственный луч. В большинстве случаев оптическая длина луча принимает минимальное значение, поэтому этот принцип называют также принципом наикратчайшего оптического пути.

В формулировке минимального светового пути этот принцип был выдвинут еще Героном Александрийским в III веке до н. э., а в формулировке минимального времени – в XVII веке Пьером Ферма.

Иллюстрация применения принципа Ферма к отражению света от поверхностей различной кривизны показан на рис. 1.9. Нетрудно доказать, что для плоской (рис. 1.9а) и выпуклой (рис. 1.9б) поверхностей из всех возможных траекторий АКВ, соединяющих точки А и В, таких, что точка К лежит на зеркале, наименьшую длину, имеет та, для которой угол падения равен

углу отражения.

Для эллиптического зеркала, у которого точки А и В являются фокусами, сумма длин отрезков АК и КВ постоянна. Поэтому оптическая длина траектории АКВ имеет стационарное значение и все реальные лучи, вышедшие из А, попадают в В. Точка В является изображением точки А, т. е. А и В – сопряженные точки. Этот пример иллюстрирует закон таутохронизма (одновременности): оптическая длина лучей между двумя сопряженными точками постоянна.

В случае когда отражение света происходит от вогнутой поверхности с кривизной большей, чем у эллипса, оптическая длина реального луча максимальна по сравнению с соседними лучами (рис. 1.9г).

Принцип Ферма может рассматриваться как основополагающий принцип геометрической оптики. Из него, так же как из уравнения эйконала, могут быть получены такие важнейшие следствия, как например

— закон прямолинейного распространения света в однородной среде;

— законы отражения и преломления на границах раздела, т. е. на тех поверхностях, где показатель преломления меняется скачком;

— траектории распространения световых лучей в неоднородной среде с непрерывно изменяющимся показателем преломления;

— закон взаимности или обратимости светового луча, в соответствии с которым траектории всех лучей, остаются без изменения при изменении их направлений распространения на противоположные.

1.5 Прохождение света через плоскую границу раздела

Предположим, что световой пучок распространяется в среде, показатель преломления которой плавно изменяется, но зависит только от одной координаты: n = n(z). Поскольку в плоскости XY показатель преломления остается постоянным, такие среды называются плоско-слоистыми. Исходя из уравнения эйконала, можно показать, что каждый световой луч в этом случае является плоской кривой, а угол q, который луч образует с осью OZ, удовлетворяет справедливому для любых зависимостей n(z) соотношению

. (1.7)

На рис. 1.10 показано распространение лучей, испущенных точечным источником, помещенным в плоско-слоистую среду. Рис. 1.10а соответствует случаю убывания функции n(z), 1.10б – возрастанию, а 1.10в – наличию минимума показателя преломления. Если луч распространяется в сторону уменьшения показателя преломления, он может углубиться в среду только на определенное расстояние, дойдя до точки поворота zп. Поскольку в точке поворота луча q = p/2 и sinq = 1, то zп определяется из соотношения , где q0 – угол выхода луча из источника, n0 – показатель преломления в месте расположения источника.

Частным, но практически наиболее важным случаем плоско-слоистых сред являются две однородные среды с показателями преломления n1 и n2 с плоской границей раздела между ними. Ось Z направлена по нормали к границе раздела.

При прохождении через такую границу раздела свет испытывает отражение и преломление (рис. 1.11). Рисунок соответствует ситуации, когда показатель преломления первой среды меньше, чем второй (n1 V2). Взаимное расположение лучей описывается законами отражения и преломления света на границе раздела. Эти законы подробно обсуждаются далее (см. Оптика, ч. 3, разделы 5.1…5.3), поэтому здесь приведем только основные формулировки.

Отражение света от границы раздела двух однородных сред

Как непосредственно вытекает из принципа Ферма и вышепреведенного анализа, луч падающий, нормаль к отражающей поверхности и луч отраженный лежат в одной плоскости (плоскости падения), которая определяется как плоскость, образованная падающим на границу раздела лучом и нормалью к границе, проведенной в точке падения луча (рис. 1.12). Углы между лучами и нормалью равны между собой: угол падения a равен углу отражения b. Установление этого закона связано с употреблением полированных металлических поверхностей (зеркал), известных уже в очень отдаленную эпоху. Построение изображения точечного источника S в плоском зеркале приведено на рис. 1.13а. В результате отражения формируется мнимое изображение S¢ источника, т. е. изображение, возникающее в точке пересечения продолжений отраженных лучей. Расстояние от зеркала до изображения b¢ равно расстоянию от источника до зеркала b.

На рис. 1.13б показано построение изображения протяженного объекта. Поскольку изображение объекта строится как совокупность изображений всех его точек, то результат для плоского зеркала очевиден: изображение получается равным, прямым и мнимым. При визуальном восприятии такого изображения правая и левая стороны как бы меняются местами.

Построение изображений в скрещенных зеркалах представлено на рис. 1.14. При отражении источника S в зеркале 1 образуется изображение S¢, которое, в свою очередь, служит источником для изображения S² в зеркале 2 (рис. 1.14а). С другой стороны, начиная построение с зеркала 2, получим изображения S²¢ и S²² (рис. 1.14б). Можно показать, что сам источник S и все формирующиеся изображения лежат на дуге одной окружности с центром в вершине зеркального угла. Кроме того, из простых геометрических соображений очевидно, что угол d между направлениями лучей до и после отражения от двух зеркал равен удвоенному углу между зеркалами: .

Последнее свойство широко используется для конструирования уголковых отражателей света (рис. 1.15). Зеркала, образующие прямой угол, возвращают все световые лучи точно в обратном направлении.

Преломление света на границе раздела двух однородных сред

Правильная формулировка этого закона принадлежит Снеллиусу и доказывается принципом Ферма. Иллюстрацией этого принципа может служить первая задача к данному разделу. Согласно закону Снеллиуса (см. рис. 1.16), луч преломленный лежит в плоскости падения, а синусы углов падения и преломления связаны соотношением

, (1.8)

которое является частным случаем общего закона (1.7).

При прохождении луча сквозь плоскопараллельную пластинку направление прошедшего луча света совпадает с направлением падающего, однако луч смещается параллельно самому себе. Расстояние х, измеренное в направлении, поперечном лучу, носит название смещения луча (рис. 1.17). Оно пропорционально толщине пластинки d и зависит от ее показателя преломления.

Если луч идет из оптически более плотной среды в менее плотную (n2