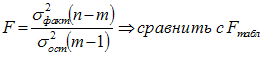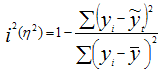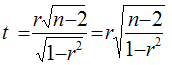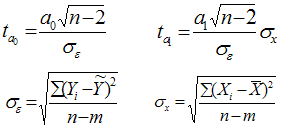Адекватность уравнения регрессии для чего

Проверка адекватности линейного уравнения регрессии

Расчет коэффициентов ПФЭ при равном числе параллельных опытов в каждой точке факторного пространства

Коэффициенты находятся по формуле:

,

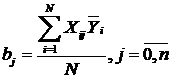
где 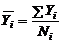— среднее значение параметра оптимизации, вычисленное по параллельным опытам – ой строки матрицы планирования .

Проверка значимости коэффициентов ПФЭ

Очевидно, что один фактор больше влияет на параметр оптимизации, другой – меньше. Поэтому можно проверить полученные коэффициенты регрессии на значимость, т.е. оценить величину влияния каждого фактора на значение параметра оптимизации. Если эта величина соизмерима с ошибкой эксперимента, то соответствующий коэффициент не несет дополнительной информации об объекте, и его можно приравнять к нулю, что упрощает математическую модель.

Значимость коэффициентов проверяется с помощью 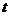– критерия Стьюдента.

Значения 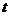– критерия вычисляются для каждого для каждого фактора по формуле:

,

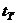
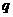
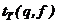
Полученные значения сравнивают с табличным значением критерия Стъюдента , которое находится по числу степеней свободы , и уровню значимости α — величина, характеризующая вероятность того, что решение будет неправильным. Обычно принимают, что α =0.05.

> ,

то коэффициент значимо отличается от нуля, если же , (1)

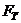
то линейное уравнение регрессии признается адекватным. Если это условие не выполняется, т.е.

При расчете F предполагается что 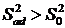. Если наблюдается обратное, то вывод об адекватности может быть сделан и без проверки условия (1).

Если модель адекватна, то ее можно использовать для поиска области оптимума объекта исследования или для предсказания отклика.

При неадекватной линейной модели наиболее часто принимают решение об уменьшении интервалов варьирования факторов и повторении эксперимента.

Итак, алгоритм расчета линейной модели с использованием ПФЭ следующий:

Задают матрицу планирования в кодированной форме для заданного числа факторов

Для каждого фактора задают базовую точку и интервал варьирования

Рассчитывают матрицу планирования в натуральной (размерной) форме

Проводят эксперименты, по матрице планирования, используя случайные числа.

Проводят серию опытов в центре плана, для определения ошибки опыта.

$ AlexLat $

Оценка значимости уравнения регрессии в целом производится на основе F-критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели. Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной (y) от среднего значения (y _ср. ) раскладывается на две части – «объясненную» и «необъясненную»:

Схема дисперсионного анализа имеет следующий вид (n –число наблюдений, m–число параметров при переменной x):

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия Фишера. Фактическое значение F -критерия Фишера сравнивается стабличным значением F _табл. (α, k ₁ , k ₂ ) при заданном уровне значимости α и степенях свободы k ₁ = m и k ₂ =n-m-1. При этом, если фактическое значение F-критерия больше табличного F _факт > F _теор , то признается статистическая значимость уравнения в целом. Для парной линейной регрессии m=1 , поэтому:

Эта формула в общем виде может выглядеть так:

Отношение объясненной части дисперсии переменной (у) к общей дисперсии называют коэффициентом детерминации и используют для характеристики качества уравнения регрессии или соответствующей модели связи. Соотношение между объясненной и необъясненной частями общей дисперсии можно представить в альтернативном варианте:

Коэффициент детерминации R 2 принимает значения в диапазоне от нуля до единицы 0≤ R 2 ≤1. Коэффициент детерминации R 2 показывает, какая часть дисперсии результативного признака (y) объяснена уравнением регрессии.Чем больше R 2 , тем большая часть дисперсии результативного признака (y) объясняется уравнением регрессии и тем лучше уравнение регрессии описывает исходные данные. При отсутствии зависимости между (у) и (x) коэффициент детерминации R 2 будет близок к нулю. Таким образом, коэффициент детерминации R 2 может применяться для оценки качества (точности) уравнения регрессии. Возникает вопрос, при каких значениях R 2 уравнение регрессии следует считать статистически незначимым, что делает необоснованным его использование в анализе? Ответ на этот вопрос дает F — критерий Фишера F _факт > F _теор — делаем вывод о статистической значимости уравнения регрессии. Величина F — критерия связана с коэффициентом детерминации R 2 _xy ( r 2 _xy ), и ее можно рассчитать по следующей формуле:

Либо при оценке значимости индекса (аналог коэффициента) детерминации:

где: i 2 — индекс (коэффициент) детерминации, который рассчитывается:

Использование коэффициента множественной детерминации R 2 для оценки качества модели, обладает тем недостатком, что включение в модель нового фактора (даже несущественного) автоматически увеличивает величину R 2 . Поэтому, при большом количестве факторов, предпочтительнее использовать, так называемый, улучшенный, скорректированный коэффициент множественной детерминации R 2 , определяемый соотношением:

где p – число факторов в уравнении регрессии, n – число наблюдений. Чем больше величина p, тем сильнее различия между множественным коэффициентом детерминации R 2 и скорректированным R 2 . При использовании скорректированного R 2 , для оценки целесообразности включения фактора в уравнение регрессии, следует учитывать, что увеличение его величины (значения), при включении нового фактора, не обязательно свидетельствует о его значимости, так как значение увеличивается всегда, когда t-статистика больше единицы (|t|>1). При заданном объеме наблюдений и при прочих равных условиях, с увеличением числа независимых переменных (параметров), скорректированный коэффициент множественной детерминации убывает. При небольшом числе наблюдений, скорректированная величина коэффициента множественной детерминации R 2 имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель. Низкое значение коэффициента множественной корреляции и коэффициента множественной детерминации R 2 может быть обусловлено следующими причинами: в регрессионную модель не включены существенные факторы; неверно выбрана форма аналитической зависимости, не реально отражающая соотношения между переменными, включенными в модель.

Для оценки значимости парного коэффициента корреляции (корень квадратный из коэффициента детерминации), при условии линейной формы связи между факторами, можно использовать t-критерий Стьюдента:

При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин. Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n t-критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t-критерия для параметров a 0 а 1 :

n-число наблюдений, m-число параметров уравнения регрессии, σ _ε -(остаточное) среднее квадратическое отклонение результативного признака от выровненных значений ŷ; σ _х -среднее квадратическое отклонение факторного признака от общей средней.

Вычисленные, по вышеприведенным формулам, значения сравнивают с критическими t, которые определяют по таблице значений Стьюдента с учетом принятого уровня значимости α и числа степеней свободы вариации k (ν)=n-2. В социально-экономических исследованиях уровень значимости α обычно принимают равным 0,05. Параметр признаётся значимым (существенным) при условии, если t _расч. > t _табл. В этом случае, практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями.

R — значит регрессия

Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.

Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.

Введение в регрессионный анализ

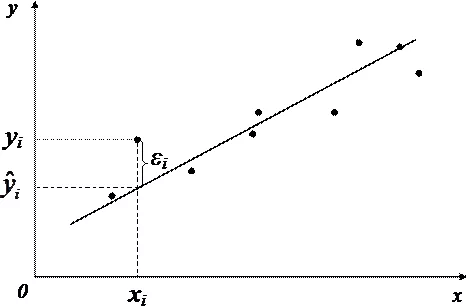
Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения называется регрессией y по x .

Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей минимальна.

Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.

Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений вокруг регрессии является дисперсия.

• k — число коэффициентов в системе уравнений регрессии.

Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x .

Линейная регрессия

Уравнения линейной регрессии можно записать в виде

В матричном виде это выгладит

• y — зависимая переменная;
• x — независимая переменная;
• β — коэффициенты, которые необходимо найти с помощью МНК;
• ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;

Случайная величина может быть интерпретирована как сумма из двух слагаемых:

• — полная дисперсия (TSS).
• — объясненная часть дисперсии (ESS).
• — остаточная часть дисперсии (RSS).

Еще одно ключевое понятие — коэффициент корреляции R 2 .

Ограничения линейной регрессии

Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.

1. Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
2. Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
3. Экзогенность независимых переменных — . Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
4. Однородность дисперсии и отсутствие автокорреляции. Каждая ε_i обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой ε_i. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.

Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.

Неоднородность дисперсии

При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.

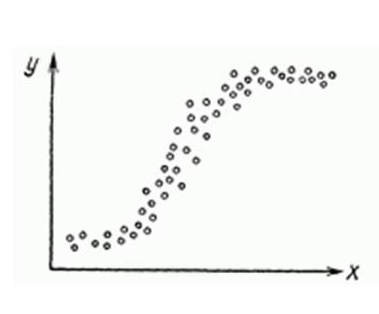
Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.

Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.

• Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4.
• Неоднородность дисперсии — Тест Уайта, , при \chi<^2>_<\alpha;m-1>$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же можно еще применить тест Бройша-Пагана.
• Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor).

В этой формуле — коэффициент взаимной детерминации между и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.

Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.

Как преодолеть эти ограничения

Нарушения одной или нескольких ограничений еще не приговор.

1. Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln .
2. Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
3. Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.

К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.

Линейная регрессия плюсов на Хабре

Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.

Загружает данные из tsv файла.

• points — Рейтинг статьи
• reads — Число просмотров.
• comm — Число комментариев.
• faves — Добавлено в закладки.
• fb — Поделились в социальных сетях (fb + vk).
• bytes — Длина в байтах.

Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.

Теперь собственно сама модель, используем функцию lm .

В первой строке мы задаем параметры линейной регрессии. Строка points

. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points

reads , набор переменных — points

Перейдем теперь к расшифровке полученных результатов.

• Intercept — Если у нас модель представлена в виде , то тогда — точка пересечения прямой с осью координат, или intercept .
• R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
• Adjusted R-squared — Проблема с в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации .
• F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
• t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
• p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.

Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.

Проверим значения параметров линейной регрессии.

Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации .

Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.

И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.

В заключение

Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.

Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.