Алгебра 10 класс мордкович тригонометрические уравнения

Методы решения тригонометрических уравнений( алгебра 10 кл, к учебнику А.Г. Мордкович)

Данная презентация подготовлена к уроку «Тригонометрические уравнения» (п.18, учебник Алгебра и начала анализа, автор А.Г.Мордкович). В презентация: 1. актуализация знаний — решение простейших уравнения, 2. Методы решения тригонометрических уравнений( введение новой переменной, разложение на множители, решение однородных уравнений первой и второй степени)

Просмотр содержимого документа
«Методы решения тригонометрических уравнений( алгебра 10 кл, к учебнику А.Г. Мордкович) »

• Повторить решение простейших тригонометрических уравнений.
• Рассмотреть способы решения тригонометрических уравнений.

Решение простейших тригонометрических уравнений:

t = ± arccos a + 2πk, k Z

t = (-1)ⁿ arcsin a + πn, n Z

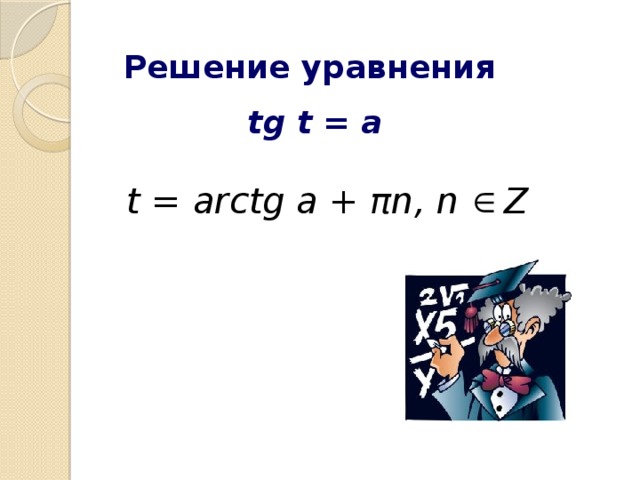
t = arctg a + πn, n Z

t = arcctg a + πn, n Z

Решение простейших тригонометрических уравнений

Решение простейших тригонометрических уравнений

Решение простейших тригонометрических уравнений

Решение простейших тригонометрических уравнений

Методы решения уравнений:

1. Введение новой переменной( №18.1-18.7)

2. Использование формул тригонометрии (18.5, 18.8)

3. Алгебраические способы:

-Вынесение множителя за скобку, группировка (18.11)

• Разложение на два уравнения (18.13).

4. Однородные линейные уравнения(деление на косинус) (18.10)

5. Однородные квадратные уравнения (деление на косинус в квадрате) (18.12)

ОДНОРОДНЫЕ И СВОДИМЫЕ К НИМ .

называется однородным уравнением I степени.

2. Уравнение вида

называется однородным уравнением II степени.

Множество значений x , удовлетворяющих уравнению

, не является решением данного уравнения. Поэтому можно обе части уравнения разделить на .

Множество значений x , удовлетворяющих уравнению , не является решением данного уравнения.

Разделим обе части уравнения на .

Уравнение примет вид:

Пример разложение на множители способом группировки:

Решение тригонометрических уравнений 10 класс апробация учебника Мордкович А. Г.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

УЧИТЕЛЬ: Азарова Ольга Геннадиевна, учитель математики ГБОУ СОШ № 32 им. Л.В.Бобковой г.Севастополя

ПРЕДМЕТ: алгебра и начала анализа

УЧЕБНИК: Мордкович А.Г. Алгебра и начала анализа.10 класс. В 2 ч. Учебник для учащихся общеобразовательных учреждения (базовый уровень) — М.:БИНОМ. Лаборатория знаний,2019

ТЕМА УРОКА: решения простейших тригонометрических уравнений и неравенств.

Образовательные: повторить, обобщить, систематизировать знания и навыки изображения решения простейших тригонометрических уравнений и неравенств на числовой окружности; напомнить основные действия с точками числовой окружности, связанные с формулами решений простейших тригонометрических уравнений. Актуализировать знания учащихся по теме «Решение простейших тригонометрических уравнений» и обеспечить их применение при решении задач вариантов ЕГЭ;

Развивающие : развивать умения учебно-познавательной деятельности, умения выделять главное, логически излагать мысли, делать выводы, расширять кругозор.

Воспитательные: воспитание ответственности, активности, побуждению интереса к математике, самостоятельности, умение работать в коллективе.

ТИП УРОКА : урок повторения и обобщения.

ОБОРУДОВАНИЕ : доска, проектор, экран, компьютер

1.Организационный момент (обеспечить внешнюю обстановку для работы на уроке, психологически настроить учащихся к общению)

2. Постановка целей .

Великий физик, математик и политик А. Эйнштейн заметил: « Мне приходиться делить время между политикой и уравнениями. Однако, уравнения гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно ».(слайд 2)

Сегодня на уроке повторяем, приводим в систему наши знания по решению простейших тригонометрических уравнений. И ваша задача – показать свои знания и умения по их решению, рассмотреть общие подходы решения тригонометрических уравнений и неравенств; закрепить навыки и проверить умение решать тригонометрические уравнения и неравенства разными способами

В начале урока мы вспомним основные понятия числовой окружности, расположение точек на числовой окружности и значения этих точек в декартовых координатах.

Далее работа будет чередоваться: вспомним формулы решения простейших тригонометрических уравнений, и на их основе посмотрим как происходит выборка корней при решении заданий ЕГЭ в 13 задании. Вспомним виды тригонометрических уравнений и неравенств. Учитывая свои знания, умения и навыки, проведём проверочные работы, задания которой вам предлагаются на листах (приложение). Решение заданий выполняются на листах, в которых предлагаются задания для самостоятельного решения. Задания Части №1выполняются по вариантам с последующей взаимопроверкой и подсчётом баллов(за каждое верное задание выставляется 1 балл).

Задания второй части решаются учащимися самостоятельно. При этом двое учащихся решают на закрытых досках. Учащихся проверяют свои решения с решением, которые проецируются на экране, и вы выставляют себе соответствующее количество баллов.

3. Актуализация опорных знаний

()учащиеся отвечают устно, при правильном ответе ставят балл в бланке ответов – приложение)

1 Продолжить определение (слайд 3)

1. Числовой прямой называется …

2. Числовой окружностью называется…

3. Синусом называется…,

4 Знаки тригонометрических функций.

5. Тригонометрические уравнения – это … ( Тригонометрические уравнения — это уравнения, в которых неизвестная находится строго под знаком тригонометрической функции .)

6. Корнем тригонометрического уравнения называется . ( Корнем тригонометрического уравнения называется такое значение входящего в него неизвестного аргумента, которое удовлетворяет этому уравнению)

Расставьте числа (слайд 4)

1 вариант: в порядке убывания: ; 3 _;2,5 ;

2 вариант : в порядке возрастания:; — ; _; ;-

2 вариант: — ; — ; -2; -;- ; —

3. Найдите значения 1 вариант 2 вариант

(слайд 6) sin (-π/3) cos (-π/4)

sin 3 π /4 cos 5 π /6

Ответы 1 вариант Ответы 2 вариант (слайд 7)

4 . (слайд 8 ) Найдите все числа, которым соответствуют отмеченные на числовой окружности точки 1 вариант 2 вариант

1 вариант: (слайд 9) 2 вариант:

t ₄ =-п/2+2пп, пеZ (3п/2+2пп, пеZ) t ₄ =7п/6+2пп, пеZ

Учащиеся подводят итоги работы 1 части: за 17-16 баллов оценка «5», за 15-12 баллов оценка «4», за 11-8 баллов оценка «3».

IV Обобщение знаний .

Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений специфична. Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнения. Запись ответа тригонометрического уравнения часто связана с понятиями объединения и пересечения множеств. Обычно при решении таких уравнений получают серии корней, и в окончательном варианте ответ записывают в виде объединения этих серий. Но как быть, если эти серии пересекаются? Сегодня мы на конкретных примерах рассмотрим различные способы и приемы при выборе ответа. Один из таких способов — геометрический. Он основан на использовании двух моделей: тригонометрической окружности и числовой прямой. Тригонометрическая окружность удобна в случае, когда речь идет об отборе корней на промежутке, длина которого не превосходит 2π, или если требуется найти наибольший отрицательный или наименьший положительный корень уравнения. В остальных случаях предпочтение отдается — числовой прямой.

Отбор корней в тригонометрическом уравнении с помощью числовой окружности.

Рассмотрим следующие примеры:

1.Изобразить на числовой окружности множество решений уравнения

sin x =/2(слайд 10)

Ответ: (1 балл)

2.Найти наименьший положительный корень sin 𝜋𝑥/ 2= 2/2. (слайд 11)

Решение: Для определения наименьшего положительного корня выбираем меньшее положительное значение 𝜋/ 4, тогда получаем

Ответ: 0,5 (2 балла)

3.На тригонометрическом круге найти корни уравнения sin 3 x =1, удовлетворяющих неравенству cos x 0.(слайд 12)

Решение: Значение sin x =1 при х = П/2 + 2 п п , п е Z

Значит 3х = П/2 + 2п п , п е Z ,

х= П/6 + 2п п/ 3, п е Z или

х= 30 0 +120 0 п, пе Z

По условию cos x 0, значит х== П/6 + 2п п, п е Z х= 3П/2 + 2п п , п е Z

Ответ: П/6 + 2п п, п е Z ; 3П/2 + 2п п , п е Z (2 балла)

Решить уравнение cos x cos 5 x =0.(слайд 13)

Решение:

(3 балла)

Найти все корни уравнения (2sinx+1)(2sinx-√3) =0, удовлетворяющие неравенству cos x ≥0 .(слайд 14)

Решение: Произведение равно нулю, если один из множителей равен нулю. Составим совокупность двух уравнений, решения системы отметим на числовой окружности. Каждому уравнению соответствуют две точки тригонометрической окружности. В ответ запишем точки, лежащие на дуге окружности при значении cos x ≥0.

(4 балла)

6. а) Решите уравнение .(слайд 15)

б) Найдите все корни этого уравнения, принадлежащие отрезку

а) Выделим полный квадрат:

б) При помощи тригонометрической окружности отберём корни, принадлежащие отрезку Получим

Ответ: а) б) (4 балла)

Ребята, сегодня повторили и систематизировали решения тригонометрических уравнений, используя различные методы решения и нахождения корней уравнений на числовой окружности.

Подведение итогов. В бланке ответов учащиеся подсчитывают набранные количество баллов за выполнение работы 2 части.

Итоги работы 2 части: за 16-15 баллов оценка «5», за 14-12 баллов оценка «4»,
за 11-8 баллов оценка «3».

Итоговая оценка за урок — среднее арифметическое оценок 1 и 2 части работы.

Решить уравнение 2 cos x = -1. В ответе укажите корень, принадлежащий промежутку [ ]

Найдите наименьший положительный корень 2sin 2х=√3.

Решите уравнение

Всем спасибо. Урок окончен. До свидания!

Тригонометрические уравнения — Тригонометрические уравнения — 1-е полугодие

Цель: рассмотреть решение тригонометрических уравнений.

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

1. Дайте определение и перечислите основные свойства функции у = arctg х.

2. Постройте график функции:

1. Дайте определение и перечислите основные свойства функции у = arcctg х.

2. Постройте график функции:

III. Изучение нового материала

Рассмотрим решение некоторых типов тригонометрических уравнений. Для этого необходимо с помощью преобразований данное уравнение свести к одному из простейших уравнений – sin x = a, cos х = a, tg х = a, ctg х = a, решение которых можно записать.

1. Простейшие тригонометрические уравнения

Еще раз напомним решения простейших тригонометрических уравнений.

1. Решения уравнений sin x = а (где |a| ≤ 1) имеют вид:

2. Решения уравнений cos x = а (где |а| ≤ 1) имеют вид:

3. Решения уравнений tg x = а имеют вид:

4. Решения уравнений ctg x = а имеют вид:

При решении уравнений sin x = 0; ±1 и cos x = 0; ±1 (частные случаи) удобнее пользоваться не общими формулами, а использовать числовую окружность, тогда получим:

Для уравнения sin x = 1 покажем предпочтительность использования числовой окружности.

Сначала запишем решения уравнения sin x = 1, применяя общую формулу Для нескольких значений n такие решения приведены в таблице.

Из данных таблицы видно, что при использовании формулы каждое решение повторяется по два раза. Кроме того, выражение более громоздко по сравнению с формулой которая получается при рассмотрении числовой окружности.

Найдем решения уравнения принадлежащие отрезку [0; π].

Решим данное уравнение, используя числовую окружность. Получим: Отберем те решения, которые принадлежат отрезку [0; π]. По условию получим неравенство Решим это неравенство: В этот промежуток попадают три целых значения n: n = 0, 1, 2. Для этих значении n найдем соответствующие решения:

Используя общую формулу, получим: Тогда

2. Два основных метода решения тригонометрических уравнений

Для решения более сложных уравнений используют метод введения новой переменной и метод разложения на множители. Рассмотрим сначала метод введения новой переменной.

а) Введем новую переменную z = cos x и получим квадратное уравнение корни которого z1 = 1 и z2 = 2/3. Вернемся к старой неизвестной и получим простейшие уравнения cos x = 1 и cos x = 2/3. Решения первого уравнения x = 2πn, решения второго уравнения

б) Используя формулу в уравнении перейдем к функции sin x. Получим: или Далее поступаем аналогично пункту а. Введем новую переменную z = sin x и получим квадратное уравнение корни которого z1 = 2 и z2 = 1/3. Вернемся к старой неизвестной и получим простейшие уравнения sin х = 2 (решений не имеет) и sin х = 1/3 (его решения ).

Теперь обсудим второй метод — метод разложения на множители. При его применении уравнение f(x) = 0 записывают в виде , тогда или f1(x) = 0, или f2(х) = 0. Таким образом, задача сводится к решению совокупности уравнений

Решим уравнение:

а) Левая часть уравнения уже разложена на множители. Задача сводится к решению совокупности уравнений tg х — 1 = 0 (или tg x = 1) и cos x + 1/2 = 0 (или cos x = -1/2). Решения первого уравнения решения второго уравнения

б) Вынесем cos 3x за скобки и получим: Теперь необходимо решить совокупность уравнений cos 3x = 0 и (или ). Решая первое уравнение, найдем: и Решая второе уравнение, получим:

Уточним рассматриваемый метод. Из уравнения следует, что или f1(x) = 0 (при этом выражение f2(х) имеет смысл), или f2(х) = 0 (при этом выражение f1(х) имеет смысл).

Решим уравнение ctg x(cos + 1) = 0.

Из уравнения ctg x = 0 находим: из уравнения cos х + 1 = 0 (или cos х = -1) получим: x = π + 2πn. Но при таких значениях х выражение ctg x не имеет смысла. Поэтому решения данного уравнения х = π/2 + пn.

3. Однородные тригонометрические уравнения

Теперь обсудим часто встречающийся вид уравнений — однородные уравнения.

Определение. Уравнение вида (где а ≠ 0, b ≠ 0) называют однородным тригонометрическим уравнением первой степени. Уравнение вида (где а ≠ 0) называют однородным тригонометрическим уравнением второй степени.

Рассмотрим сначала решение однородных тригонометрических уравнений первой степени Убедимся, что cos х ≠ 0. Предположим, что cos х = 0, и подставим эту величину в данное уравнение. Получим: a sin х = 0. Так как а ≠ 0, то sin x = 0. Очевидно, что равенства cos x = 0 и sin x = 0 одновременно выполняться не могут, так как равенство sin2x + cos2x = 1 не выполняется.

Так как cos x ≠ 0, то разделим все члены уравнения на cos x. Получим: или откуда и

Решим уравнение

Разделим все члены уравнения на и получим: Найдем и

Решим уравнение

Учтем четность функции косинуса и формулы приведения. Получим: или Разделим обе части уравнения на cos 3x. Имеем: 2tg 3x = -1, откуда tg 3x = -1/2,

Рассмотрим теперь решение однородного тригонометрического уравнения второй степени Убедимся, что cos х ≠ 0. Подставим значение cos х = 0 в данное уравнение и получим: a sin2 х = 0. Так как а ≠ 0, то имеем: sin х = 0. Но равенства cos х = 0 и sin х = 0 одновременно выполняться не могут.

Так как cos x ≠ 0, то разделим все члены уравнения на cos2x и получим: или Введем новую переменную z = tg x и придем к квадратному уравнению az2 + bz + c = 0. Решаем это уравнение. Потом возвращаемся к старой переменной, получаем простейшие тригонометрические уравнения и находим их решения.

Решим уравнение

Разделим все члены уравнения на cos2 x и получим: tg2 x – tg x — 2 = 0. Введем новую переменную z = tg x и получим квадратное уравнение z2 — z — 2 = 0, корни которого z1 = -1 и z2 = 2. Вернемся к старой переменной. Имеем простейшие тригонометрические уравнения tg х = -1 (его решения ) и tg х = 2 (его решения ).

Решим уравнение

Данное уравнение не является однородным, так как в правой части стоит число 1, а не число 0. Если учесть равенство sin2 х +cos2 х = 1, то уравнение легко свести к однородному. Получим: или Разделим все члены уравнения на cos2 x. Имеем: tg2 x + 5tg x + 4 = 0. Введем новую переменную z = tg x и получим квадратное уравнение z2 + 5z + 4 = 0, корни которого z1 = -1 и z2 = -4. Вернемся к старой переменной. Получим простейшие тригонометрические уравнения tg x = -1 (его решения ) и tg х = -4 (его решения ).

Пусть в однородном тригонометрическом уравнении коэффициент a = 0. Тогда уравнение имеет вид: В этом случае делить на cos2 x нельзя, так как cos х может равняться нулю. Поэтому надо использовать метод разложения на множители. Получим Имеем простейшее тригонометрическое уравнение cos x = 0 и однородное тригонометрическое уравнение первой степени Такие уравнения мы решать уже умеем.

Решим уравнение

Разложим левую часть уравнения на множители: Произведение двух множителей равно нулю. Поэтому один из множителей равен нулю. Получаем простейшее тригонометрическое уравнение cos х = 0 (его решения ) и однородное тригонометрическое уравнение первого порядка или (его решения ).

Метод разложения на множители также используется и в случае, когда коэффициент с = 0. Тогда уравнение имеет вид: или Вновь получаем простейшее тригонометрическое уравнение sin х = 0 и однородное тригонометрическое уравнение первого порядка которые решаются аналогично примеру 11.

Рассмотрение примеров 9-11 позволяет сформулировать алгоритм решения уравнения

1. Если коэффициент а не равен нулю, то все члены уравнения делят на cos2 x. Вводят новую переменную z = tg х и получают квадратное уравнение. Находят корни этого уравнения и возвращаются к старой неизвестной. Получают простейшие тригонометрические уравнения и решают их.

2. Если коэффициенты а и с равны нулю, то используют метод разложения на множители. При a = 0 выносят за скобки cos х, при с = 0 выносят sin x. Получают простейшее тригонометрическое уравнение и однородное тригонометрическое уравнение первого порядка и решают их.

IV. Контрольные вопросы

1. Решения простейших тригонометрических уравнений.

2. Два основных метода решения тригонометрических уравнений.

3. Определение однородного тригонометрического уравнения первой и второй степеней.

4. Решение однородного тригонометрического уравнения первой степени.

5. Алгоритм решения однородного тригонометрического уравнения второй степени.

V. Задание на уроках

§ 18, № 3 (а, в); 5 (а, б); 6 (б); 8 (г); 10 (а, б); 11 (в); 12 (а); 13 (в); 16; 18; 20 (а); 21 (а, б); 23 (а); 27 (а, б); 30 (а); 31; 33 (а); 34 (б); 35 (а).

VI. Задание на дом

§ 18, № 3 (б, г); 5 (в, г); 6 (г); 8 (б); 10 (в, г); 11 (а); 12 (б); 13 (г); 17; 19; 20 (б); 21 (в, г); 23 (б); 27 (в, г); 30 (б); 32; 33 (б); 34 (а); 35 (б).

VII. Подведение итогов уроков

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2022 Все права на дизайн сайта принадлежат С.Є.А.