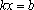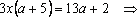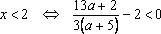Алгебра 11 класс решение уравнений с параметром

Уравнения с параметрами
план-конспект урока по алгебре (11 класс) по теме

Урок по теме: «Уравнения с параметрами»

1. Знать, что такое уравнение с параметрами, что значит решить такое уравнение.

2. Уметь решать простейшие уравнения с параметрами.

3. Развивать интерес к заданиям исследовательского характера.

1. Организационная часть.

2. Повторение пройденных тем.

3. Изучение нового материала.

4. Закрепление изученного.

5. Домашнее задание.

Скачать:

Предварительный просмотр:

Урок по теме: «Уравнения с параметрами»

1. Знать, что такое уравнение с параметрами, что значит решить такое уравнение.
2. Уметь решать простейшие уравнения с параметрами.
3. Развивать интерес к заданиям исследовательского характера.

1. Организационная часть.
2. Повторение пройденных тем.
3. Изучение нового материала.
4. Закрепление изученного.
5. Домашнее задание .

1. Организация урока.

Урок начинается с приветствия. Объявляется тема урока и задачи. Нацелить учащихся на важность изучаемого материала не только для подготовки к экзаменам в школе, но и при подготовке к поступлению в вузы.

1) Определите тип уравнения. Сколько корней у него может быть? Решите его.

а) 3х – 6 = 0, 0х = 5, 0х = 0.

ах = в — линейное

а 0 х = — один корень,

а = о, в 0 — нет корней,

а = 0, в = 0 — х – любое число.

б) 2х 2 – 3х + 6 = 0

Измените условие так, чтобы полученное уравнение имело два корня.

ах 2 + вх + с = 0 , а 0 — квадратное

1. Если Д > 0, то 2 корня,

2. Если Д = 0, то 1 корень,

Измените условие так, чтобы полученное уравнение не имело корней.

Измените условие так, чтобы полученное уравнение не имело корней.

х при х > 0,
— х при х

2) Чем отличаются уравнения а х = в и 3х = 6, а х 2 + в х + с = 0 и 2х 2 –3х+6 = 0?

(Ответ учащихся: в первом и третьем уравнениях не числовые коэффициенты).

Учитель: Действительно, в уравнениях а х = в и а х 2 + в х + с = 0 не числовые коэффициенты, а буквенные. Именно такие уравнения и станут предметом нашего изучения на уроке

3. Изучение нового материала.

1) Определение . Уравнение, в котором помимо переменной содержится буквенное выражение, называется уравнением с параметрами.

Примеры: а x + в = 0 (x – переменная, а и в – параметры),

а x 2 + в x + с = 0 (x – переменная, а, в и с – параметры).

2) Чаще всего встречаются две постановки задач.

Первая: для каждого значения параметра найти все решения заданного уравнения.

Вторая: найти все значения параметра, при каждом из которых решения уравнения удовлетворяют заданным условиям.

Пример: ( а – 2)х 2 + 3х – 4 = 0

Первая постановка задачи: решите уравнение. Это значит, что для каждого значения параметра а , необходимо найти решения.

Вторая постановка задачи: при каких значениях параметра а уравнение имеет два различных корня.

Определение. Решить уравнение с параметром – значит, для любого допустимого значения параметра найти множество всех корней заданного уравнения.

1). Простые уравнения без ветвлений:

а) x – а = 0 Ответ: при а ( — , + ) х = а .

б) 5x = а Ответ: при а ( — , + ) х = .

в) x : 2 = а Ответ: при а (- , + ) х = 2 а .

г) [x] = [ а ] Ответ: при а (- , + ) х = ± а .

д) x 3 = а Ответ: при а (- , + ) х = .

2). Простые уравнения с ветвлениями:

а) а x = 10 Ответ: при а 0 х = , при а = 0 решений нет.

б) 0x = а Ответ: при а 0 корней нет, при а = 0 х – любое число.

в) [х] = а Ответ: при а а = 0 х = 0, при а > о х = а.

г) ( а 2 – 4)x = а 2 + а – 6

Решение г). Если а 2 – 4 0, т.е. а ± 2, то х = .

При а = -2 уравнение имеет вид: 0х = -4, т.е. не имеет корней.

При а = 2 исходное уравнение принимает вид: 0х = 0, т.е. х – любое число.

Ответ: при а ± 2 х = ,

при а = — 2 корней нет,

при а = 2 х – любое число.

(Обратить внимание учащихся на тот факт, что при решении данного уравнения получили исключение для параметра. В таких случаях необходимо делать проверку (испытание) для каждого исключения: подставить значение параметра в исходное уравнение и решить его).

Решение: х 2, тогда а = х – 2 или х = а + 2.

Найдем а , при котором х = 2

Итак, при а = 0 х = 2, но это посторонний корень.

Ответ: при а = 0 корней нет, при а 0 х = а + 2.

2) ( а – 2)х 2 + 3х – 4 = 0.

(Обратить внимание учащихся на то, что в ходе решения уравнения 1) появилось исключение для х. В таком случае необходимо найти значение параметра, при котором есть исключение для переменной).

Повторить основные этапы решения уравнений с параметрами.

Домашнее задание: опорный конспект и решение уравнений (примерный набор заданий – карточки).

Урок по теме: «Уравнения с параметрами». 11-й класс

Разделы: Математика

Класс: 11

Цели:

1. Знать, что такое уравнение с параметрами, что значит решить такое уравнение.
2. Уметь решать простейшие уравнения с параметрами.
3. Развивать интерес к заданиям исследовательского характера.

Ход урока

1. Организация урока.

На классной доске — дата, тема урока, оформлены записи (элементы опорного конспекта), опорный конспект по повторению, задачи для устной работы.

На рабочих местах учащихся – опорные конспекты, карточки с заданиями.

Урок начинается с приветствия. Объявляется тема урока и задачи. Нацелить учащихся на важность изучаемого материала не только для подготовки к экзаменам в школе, но и при подготовке к поступлению в вузы.

2. Устные упражнения.

1) Определите тип уравнения. Сколько корней у него может быть? Решите его.

а) 3х – 6 = 0, 0х = 5, 0х = 0.

Работа с опорным конспектом по повторению:

ах = в — линейное

а 0 х = — один корень,

а = о, в 0 — нет корней,

а = 0, в = 0 — х – любое число.

б) 2х 2 – 3х + 6 = 0

Д 2 + вх + с = 0 , а 0 — квадратное

1. Если Д > 0, то 2 корня,

2. Если Д = 0, то 1 корень,

3. Если Д 0,
— х при х 2 + вх + с = 0 и 2х 2 –3х+6 = 0?

(Ответ учащихся: в первом и третьем уравнениях не числовые коэффициенты).

Учитель: Действительно, в уравнениях ах = в и ах 2 + вх + с = 0 не числовые коэффициенты, а буквенные. Именно такие уравнения и станут предметом нашего изучения на уроке. Работать будем с опорными конспектами.

3. Изучение нового материала.

1) Определение. Уравнение, в котором помимо переменной содержится буквенное выражение, называется уравнением с параметрами.

Примеры: аx + в = 0 (x – переменная, а и в – параметры),

аx 2 + вx + с = 0 (x – переменная, а, в и с – параметры).

2) Чаще всего встречаются две постановки задач.

Первая: для каждого значения параметра найти все решения заданного уравнения.

Вторая: найти все значения параметра, при каждом из которых решения уравнения удовлетворяют заданным условиям.

Пример: (а – 2)х 2 + 3х – 4 = 0

Первая постановка задачи: решите уравнение. Это значит, что для каждого значения параметра а, необходимо найти решения.

Вторая постановка задачи: при каких значениях параметра а уравнение имеет два различных корня.

Определение. Решить уравнение с параметром – значит, для любого допустимого значения параметра найти множество всех корней заданного уравнения.

Решение уравнений. (Работа с опорными конспектами. Учащиеся привлекаются к поиску ответов).

1). Простые уравнения без ветвлений:

а) x – а = 0 Ответ: при а ( — , + ) х = а.

б) 5x = а Ответ: при а ( — , + ) х = .

в) x : 2 = а Ответ: при а (- , + ) х = 2а.

г) [x] = [а] Ответ: при а (- , + ) х = ± а.

д) x 3 = а Ответ: при а (- , + ) х = .

2). Простые уравнения с ветвлениями:

а) аx = 10 Ответ: при а 0 х = , при а = 0 решений нет.

б) 0x = а Ответ: при а 0 корней нет, при а = 0 х – любое число.

в) [х] = а Ответ: при а о х = а.

Решение г). Если а 2 – 4 0, т.е. а ± 2, то х = .

При а = -2 уравнение имеет вид: 0х = -4, т.е. не имеет корней.

При а = 2 исходное уравнение принимает вид: 0х = 0, т.е. х – любое число.

Ответ: при а ± 2 х = ,

при а = — 2 корней нет,

при а = 2 х – любое число.

(Обратить внимание учащихся на тот факт, что при решении данного уравнения получили исключение для параметра. В таких случаях необходимо делать проверку (испытание) для каждого исключения: подставить значение параметра в исходное уравнение и решить его).

4. Закрепление. (Коллективный поиск решения, оформление решения на доске и в тетрадях учащихся).

= 1

Решение: х 2, тогда а = х – 2 или х = а + 2.

Найдем а, при котором х = 2

Итак, при а = 0 х = 2, но это посторонний корень.

Ответ: при а = 0 корней нет, при а 0 х = а + 2.

2) (а – 2)х 2 + 3х – 4 = 0.

(Обратить внимание учащихся на то, что в ходе решения уравнения 1) появилось исключение для х. В таком случае необходимо найти значение параметра, при котором есть исключение для переменной).

Повторить основные этапы решения уравнений с параметрами.

Домашнее задание: опорный конспект и решение уравнений (примерный набор заданий – карточки).

2) = 0,

Задачи с параметрами для 10-11 класса

Задачи с параметрами

(10 – 11 классы)

Параметры – это те же числа, просто заранее не известные.

1. Линейные уравнения и неравенства с параметрами

Линейная функция: — уравнение прямой с угловым коэффициентом . Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси .

Линейные уравнения с параметрами

Если , уравнение имеет единственное решение.

Если , то уравнение не имеет решений, когда , и уравнение имеет бесконечно много решений, когда .

Пример 1. При всех значениях параметра а решить уравнение: (a2 – 4)x = a + 2

Решение: Разложим коэффициент при на множители. .

Если , уравнение имеет единственное решение: .

Если , уравнение не имеет решений.

Если , то уравнение имеет бесконечно много решений .

Пример 2. При всех значениях параметра а решить уравнение: .

Решение: ОДЗ: . При этом условии уравнение равносильно следующему: . Проверим принадлежность к ОДЗ: , если . Если же , то уравнениене имеет решений.

Пример 3. При всех значениях параметра а решить уравнение:

Решение: Разобьем числовую прямую на 3 части точками, в которых выражения под знаком модуля обращаются в нуль и решим 3 системы:

1) , если . Найденный будет решением, если .

2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же

, то решением является любой .

3) , если . Найденный не удовлетворяет нужному неравенству, следовательно, не является решением при . Если же

, то решением является любой . Сформируем

Ответ: при ; при ;

при ; является также решением при всех .

Пример 4. Найти все а , при каждом из которых хотя бы одно из решений уравнения 15x – 7a = 2 – 3ax + 6a меньше 2 .

Решение: Найдем решения уравнения при каждом . , если . Решим неравенство:

При уравнение не имеет решений.

Ответ: а Î (-5, 4).

Линейные неравенства с параметрами

Пример 1. Решить неравенство:

Если , то . Если , то . Если , то при решением является любой , а при решений нет.

Аналогично решите остальные неравенства в рамочке.

Пример 2. Для всех значений параметра а решить неравенство

Решение. . Если скобка перед положительна, т.е. при , то . Если скобка перед отрицательна, т.е. при

, то . Если же или , то решений нет.

Пример 3. Для всех значений параметра а решить неравенство

Просмотр содержимого документа
«Задачи с параметрами для 10-11 класса »

Параметры – это те же числа, просто заранее не известные.

1. Линейные уравнения и неравенства с параметрами

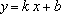
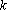
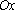
Линейная функция: — уравнение прямой с угловым коэффициентом . Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси .

Линейные уравнения с параметрами

Уравнение

Если 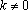, уравнение имеет единственное решение.

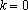
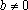
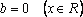
Если , то уравнение не имеет решений, когда , и уравнение имеет бесконечно много решений, когда .

Пример 1. При всех значениях параметра а решить уравнение: (a 2 – 4)x = a + 2

Решение: Разложим коэффициент при на множители. .

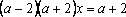
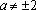
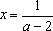
Если , уравнение имеет единственное решение: .

Если 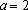, уравнение не имеет решений.

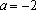
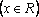
Если , то уравнение имеет бесконечно много решений .

Пример 2. При всех значениях параметра а решить уравнение: .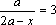

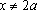
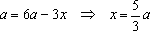
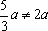
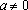
Решение: ОДЗ: . При этом условии уравнение равносильно следующему: . Проверим принадлежность к ОДЗ: , если . Если же , то уравнениене имеет решений.

Пример 3. При всех значениях параметра а решить уравнение:

Решение: Разобьем числовую прямую на 3 части точками, в которых выражения под знаком модуля обращаются в нуль и решим 3 системы:

1) , если . Найденный будет решением, если .

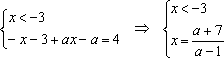
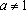
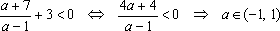
2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же

, то решением является любой .

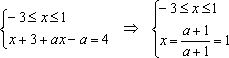
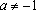
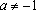
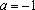
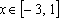
3) , если . Найденный не удовлетворяет нужному неравенству, следовательно, не является решением при . Если же

, то решением является любой . Сформируем

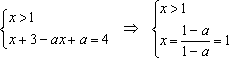
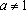
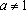
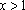
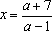
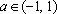
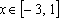
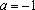
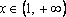
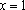
Ответ: при ; при ;

при ; является также решением при всех .

Пример 4. Найти все а , при каждом из которых хотя бы одно из решений уравнения 15x – 7a = 2 – 3ax + 6a меньше 2 .

Решение: Найдем решения уравнения при каждом . , если . Решим неравенство:

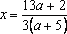
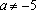
При уравнение не имеет решений.

Линейные неравенства с параметрами

Пример 1. Решить неравенство:

Если , то . Если , то . Если 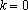, то при решением является любой , а при решений нет.

Аналогично решите остальные неравенства в рамочке.

Пример 2. Для всех значений параметра а решить неравенство

Решение. . Если скобка перед положительна, т.е. при , то . Если скобка перед отрицательна, т.е. при

, то . Если же или , то решений нет.

Пример 3. Для всех значений параметра а решить неравенство

Решение. При имеем неверное неравенство , т.е. решений нет. Пусть , тогда при оба модуля раскрываются с минусом и получаем неверное неравенство , т.е. решений нет. Если , то первый модуль раскрывается с минусом, а второй с плюсом и получаем неравенство , т.е. , т.е., решением является любой . Если оба модуля раскрываются с плюсом и получаем верное неравенство , т.е. , решением является любой . Объединяя оба ответа, получим, что при .

Пусть , тогда первое слагаемое больше, чем второе, поэтому разность в левой части неравенства положительна и, следовательно, не может быть меньше отрицательного числа . Т.о., при решений нет.

Ответ. При , при решений нет.

Замечание. Решении данной задачи получается быстрее и проще, если использовать геометрическую интерпретацию модуля разности двух чисел, как расстояние между точками. Тогда выражение в левой части можно интерпретировать, как разность расстояний от точки х до точек а и -а .

Пример 4. Найти все а , при каждом из которых все решения неравенства удовлетворяют неравенству .

Решение. Решением неравенства является множество , а решением неравенства является множество . Чтобы

удовлетворить условию задачи, нужно, чтобы множество А входило в множество В ( ). Это условие выполнится тогда и только тогда, когда

Пример 5. Найти все значения a , при которых неравенство выполняется для всех x из отрезка [1, 3] .

Решение. Дробь – меньше нуля между корнями, поэтому надо

выяснить, какой корень больше. и

. Т.о., при и чтобы неравенство выполнялось для всех x из отрезка [1, 3], нужно, чтобы

При и чтобы неравенство выполнялось для всех x из отрезка [1, 3], нужно, чтобы .

При (когда корни совпадают) решений нет, т.к. в этом случае неравенство приобретает вид : .

Пример 6. При каких значениях параметра а неравенство справедливо при всех отрицательных значениях х ?

Решение. Функция монотонно возрастает, если коэффициент при неотрицательный, и она монотонно убывает, если коэффициент при отрицательный.

Выясним знак коэффициента при . . .

Пусть . Тогда функция монотонно не убывает, и условие задачи будет выполнено, если

. Вместе с условиями получим : .

Пусть . Тогда функция монотонно убывает, и условие задачи никогда не может быть выполнено.

2. Векторы на плоскости

Пусть два вектора на плоскости заданы своими координатами:

Модуль (длина) вектора: .

где — угол между векторами.

Условие параллельности двух векторов: . Т.е.

у параллельных векторов координаты пропорциональны.

Условие перпендикулярности двух векторов: . Т.е. два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

Если вектор задан своими концами и , то вектор .

Задача 1. Через точку провести прямую, параллельную вектору .

Решение. Пусть точка — текущая точка искомой прямой. Тогда вектор параллелен вектору . Тогда выписывая условие параллельности, получим уравнение искомой прямой:

Переписав в виде , получим уравнение с угловым коэффициентом , проходящей через заданную точку .

Задача 2. Через точку провести прямую, перпендикулярную вектору . Вектор , перпендикулярный прямой, называется нормальным вектором к прямой илинормалью к прямой.

Решение. Пусть точка — текущая точка искомой прямой. Тогда вектор перпендикулярен вектору . Тогда выписывая условие перпендикулярности, получим уравнение искомой прямой:

Раскрыв скобки и обозначив число , получим так называемое общее уравнение прямой:

В этом уравнении коэффициенты при и являются координатами нормального вектора прямой.

Всякая прямая разбивает плоскость на две полуплоскости, где с одной стороны прямой и с другой стороны. При этом точки той

части плоскости, куда смотрит вектор , удовлетворяет неравенству . Поэтому:

В направлении вектора функция возрастает, а в направлении вектора она убывает.

Пример 5. Написать уравнение прямой, проходящей через точку параллельно прямой .

Решение. У параллельных прямых нормальные вектора тоже параллельны, т.е. . Согласно задаче 2 получим искомое уравнение: или .

3. Системы двух линейных уравнений с параметрами

Решениями системы двух линейных уравнений являются точки пересечения двух прямых: и .

Возможны 3 случая:

1. Прямые не параллельны . Тогда и их нормальные вектора не параллельны, т.е. . В этом случае система имеет единственное решение.

2. Прямые параллельны и не совпадают. Тогда и их нормальные вектора параллельны, но сдвиги различны, т.е. .

В этом случае система решений не имеет .

3. Прямые совпадают. Тогда их нормальные вектора параллельны и сдвиги совпадают, т.е. . В этом случае система имеет бесконечно много решений – все точки прямой.

Пример 1. При всех значениях а и b решить систему уравнений

Решение. Выразим из первого уравнения и подставим во второе уравнение. Получим: .

Если — единственное решение. Если , то если , то решений бесконечно много: . Если

же , то решений нет.

Пример 2. При каком значении параметра а система уравнений

Решение. Система не имеет решений, если .

Пример 3. При всех значениях а решить систему уравнений

Решение. Система равносильна совокупности двух систем:

Прямые параллельны , если . При этом прямые не совпадают, поэтому при 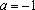решений нет.

Если 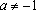, то выражая из второго уравнения и подставляя в первое, получим: .

Пример 4. Найти все такие значения а, что для любого значения b

найдётся хотя бы одно с такое, что система уравнений

имеет хотя бы одно решение.

Решение. Прямые не параллельны, если

В этом случае система имеет единственное решение при любом c.

По условию задачи система должна иметь решение при всех b.

Если то система принимает вид: . Чтобы при система также имела решения, нужно, чтобы уравнение относительно c имело хотя бы одно решение. Т.о., дискриминант этого уравнения должен быть неотрицательным, т.е.

Аналогично, если то система принимает вид: Чтобы при система также имела решения, нужно, чтобы уравнение

относительно c имело хотя бы одно решение. Т.о., дискриминант этого уравнения должен быть неотрицательным, т.е.

4. Системы двух линейных неравенств с параметрами

Пример 1. При каких значениях а система неравенств

не имеет решений?

Решение. Система имеет решения только если .

Ответ: при решением будет любой ;

при решений нет.

Пример 2. При каких значениях а система неравенств

имеет хотя бы одно решение?

Решение. При первое неравенство не имеет решений. А тогда и вся система не имеет решений.

Пусть , тогда и эта система не имеет решений, так как , а . Пусть , тогда т.е.

решения есть при , и , так как при выполнено неравенство , то решение запишется в виде .

Ответ: при решением будет любой ;

при решений нет.

Пример 3. При всех значениях а решить систему

Решение. Перепишем систему неравенств в виде . Рассмотрим все возможные случаи.

1) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем: при

2) . Тогда первое неравенство не верно. А значит, и вся система не имеет решений .

3) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем:

4) . Тогда второе неравенство не верно. А значит, и вся система не имеет решений .

5) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем: при

при и при решений нет.

Пример 4. При всех значениях а решить систему

При система не имеет решений.

Пусть , тогда и эта система не имеет решений.

Пусть , тогда и эта система будет иметь решения, если выполнено неравенство: .