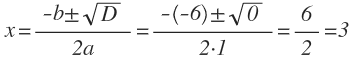Алгебра 8 класс дискриминант примеры уравнения

Как найти дискриминант квадратного уравнения

О чем эта статья:

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Квадратные уравнения (8 класс)

Уравнение называют квадратным, если его можно записать в виде \(ax^2+bx+c=0\), где \(x\) неизвестная, \(a\), \(b\) и \(с\) коэффициенты (то есть, некоторые числа, причем \(a≠0\)).

В первом примере \(a=3\), \(b=-26\), \(c=5\). В двух других \(a\),\(b\) и \(c\) не выражены явно. Но если эти уравнения преобразовать к виду \(ax^2+bx+c=0\), они обязательно появятся.

Коэффициент \(a\) называют первым или старшим коэффициентом, \(b\) – вторым коэффициентом, \(c\) – свободным членом уравнения.

Виды квадратных уравнений

Если в квадратном уравнении присутствуют все три его члена, его называют полным. В ином случае уравнение называется неполным.

Как решать квадратные уравнения

В данной статье мы рассмотрим вопрос решения полных квадратных уравнений. Про решение неполных — смотрите здесь .

Итак, стандартный алгоритм решения полного квадратного уравнения:

Преобразовать уравнение к виду \(ax^2+bx+c=0\).

Выписать значения коэффициентов \(a\), \(b\) и \(c\).
Пока не отработали решение квадратных уравнений до автоматизма, не пропускайте этот этап! Особенно обратите внимание, что знак перед членом берется в коэффициент. То есть, для уравнения \(2x^2-3x+5=0\), коэффициент \(b=-3\), а не \(3\).

Вычислить значение дискриминанта по формуле \(D=b^2-4ac\).

Решите квадратное уравнение \(2x(1+x)=3(x+5)\)
Решение:

Теперь переносим все слагаемые влево, меняя знак.

Уравнение приняло нужный нам вид. Выпишем коэффициенты.

Найдем дискриминант по формуле \(D=b^2-4ac\).

Найдем корни уравнения по формулам \(x_1=\frac<-b + \sqrt><2a>\) и \(x_2=\frac<-b - \sqrt><2a>\).

Решите квадратное уравнение \(x^2+9=6x\)
Решение:

Тождественными преобразованиями приведем уравнение к виду \(ax^2+bx+c=0\).

Найдем дискриминант по формуле \(D=b^2-4ac\).

Найдем корни уравнения по формулам \(x_1=\frac<-b + \sqrt><2a>\) и \(x_1=\frac<-b - \sqrt><2a>\).

В обоих корнях получилось одинаковое значение. Нет смысла писать его в ответ два раза.

Решите квадратное уравнение \(3x^2+x+2=0\)
Решение:

Уравнение сразу дано в виде \(ax^2+bx+c=0\), преобразования не нужны. Выписываем коэффициенты.

Найдем дискриминант по формуле \(D=b^2-4ac\).

Найдем корни уравнения по формулам \(x_1=\frac<-b + \sqrt><2a>\) и \(x_1=\frac<-b - \sqrt><2a>\).

Оба корня невычислимы, так как арифметический квадратный корень из отрицательного числа не извлекается.

Обратите внимание, в первом уравнении у нас два корня, во втором – один, а в третьем – вообще нет корней. Это связано со знаком дискриминанта (подробнее смотри тут ).

Также многие квадратные уравнения могут быть решены с помощью обратной теоремы Виета . Это быстрее, но требует определенного навыка.

Пример. Решить уравнение \(x^2-7x+6=0\).
Решение: Согласно обратной теореме Виета, корнями уравнения будут такие числа, которые в произведении дадут \(6\), а в сумме \(7\). Простым подбором получаем, что эти числа: \(1\) и \(6\). Это и есть наши корни (можете проверить решением через дискриминант).
Ответ: \(x_1=1\), \(x_2=6\).

Данную теорему удобно использовать с приведенными квадратными уравнениями, имеющими целые коэффициенты \(b\) и \(c\).

Формула корней квадратного уравнения

Дискриминант и решение квадратного уравнения

Решим квадратное уравнение $ax^2+bx+c = 0, a \neq 0$ в общем виде:

$$ ax^2+bx+c=0 | \times 4a $$

$$ 4a^2 x^2+4abx+4ac = 0 |+b^2 $$

$$ ((2ax)^2+2 \cdot 2ax\cdot b+b^2 )+4ac = b^2 $$

Если выражение справа неотрицательное, то:

И решение нашего уравнения:

Выражение $D = b^2-4ac$ называют дискриминантом квадратного уравнения $ax^2+bx+c = 0$.

Если $D \gt 0$, то квадратное уравнение имеет два корня: $x_ <1,2>= \frac<-b \pm \sqrt><2a>$

Если D = 0, то квадратное уравнение имеет один корень: $x = — \frac<2a>$

Если $D \lt 0$, то квадратное уравнение решений не имеет, $x \in \varnothing$

Количество корней квадратного уравнения

Общий алгоритм решения квадратного уравнения

Ниже представлен полный алгоритм решения квадратного уравнения на множестве действительных чисел.

В зависимости от выполнения условий (в ромбах), в алгоритме происходит ветвление. Всего на ветках «вырастает» 11 листьев – 11 возможных решений.

Если условие в ромбе выполняется, выход обозначен синей веткой, не выполняется – красной. Над некоторыми ветками для наглядности представлены текущие значения параметров.

В простейшем (в математике говорят, «тривиальном») случае, при всех нулевых коэффициентах, уравнение имеет бесконечное множество решений.

Три ветки заканчиваются пустым множеством, с отсутствием решений.

Четыре ветки дают по одному корню, и три ветки дают по два корня.

Примеры

Пример 1. Решите уравнение, вычислив дискриминант:

$$ D = 24^2-4 \cdot 5 \cdot (-5) = 576+100 = 676 = 26^2 $$

$$ D = 19^2-4 \cdot 3 \cdot (-14) = 361+168 = 529 = 23^2 $$

$$ D = 4^2-4 \cdot 12 \cdot (-1) = 16+48 = 64 = 8^2 $$

$$ D = 24^2-4 \cdot 16 \cdot 9 = 576-576 = 0 $$

$$D = 53^2-4 \cdot 7 \cdot (-24) = 2809+672 = 3481 = 59^2$$

$$ D = 3^2-4 \cdot 6 \cdot 4 = 9-96 = -87 \lt 0 $$

$x \in \varnothing$, решений нет

Пример 2. Решите уравнения:

$D = 4^2-4 \cdot 1 \cdot (-32) = 16+128 = 144 = 12^2 $

$ x = \frac<-4 \pm 12> <2>= \left[ \begin x_1 = -8 \\ x_2 = 4 \end \right. $

$ \frac<2x^2> = -\frac<1> <24>\Rightarrow 48x^2 = -(x^2-49) \Rightarrow 49x^2 = 49 \Rightarrow x^2 = 1 \Rightarrow x_1,2 = \pm 1 $

$$ \Rightarrow 4x^2-7x-6 = 3(x^2-4) \Rightarrow x^2-7x+6 = 0$$

$$ D = 7^2-4 \cdot 6 = 49-24 = 25 = 5^2$$

$$ x = \frac<7 \pm 5> <2>= \left[ \begin x_1 = 1 \\ x_2 = 6 \end \right.$$

$$ 3y^2+y = y^2+11y-12 \Rightarrow 2y^2-10y+12 = 0 \Rightarrow y^2-5y+6 = 0 $$

$$ D = 5^2-4 \cdot 6 = 1 $$

$$ x = \frac<5 \pm 1> <2>= \left[ \begin y_1 = 2 \\ y_2 = 3 \end \right.$$

Пример 3*. Решите уравнение:

$$ \frac <|x|>= \frac <|x|>x = \left[ \begin -x, x \lt 0 \\ x, x \gt 0 \end \right. $$

$$ x^2-5 \frac<|x|>-6 = 0 \Rightarrow \left[ \begin x^2+5x-6 = 0, x \lt 0 \\ x^2-5x-6 = 0, x \gt 0 \end \right. $$

Корни каждого из уравнений:

$$ D = 5^2-4 \cdot (-6) = 25+24 = 49 = 7^2, x = \frac<-5 \pm 7> <2>= \left[ \begin x_1 = -6 \\ x_2 = 1 \end \right. $$

$$ D = (-5)^2-4 \cdot (-6) = 25+24 = 49 = 7^2, x = \frac<5 \pm 7> <2>= \left[ \begin x_3 = -1 \\ x_4 = 6 \end \right. $$

$$ \left[ \begin \left[ \begin x_1 = -6 \\ x_2 = 1 \end \right. ,x \lt 0 \\ \left[ \begin x_3 = -1 \\ x_4 = 6 \end \right. ,x \gt 0 \end \right. \Rightarrow \left[ \begin x_1 = -6 \\ x_2 = 6 \end \right. $$

$$ \left[ \begin -x^2-4x-4 = 0, x \lt 0 \\ x^2-4x-4 = 0, x \gt 0 \end \right. \Rightarrow \left[ \begin x^2+4x+4 = 0, x \lt 0 \\ x^2-4x-4 = 0, x \gt 0 \end \right. $$

Корни каждого из уравнений:

$$ x^2+4x+4 = (x+2)^2 = 0 \Rightarrow x = -2 $$

$$ D = 4^2-4 \cdot (-4) = 16+16 = 32, \sqrt = \sqrt <16 \cdot 2>= 4\sqrt <2>$$

$$ \left[ \begin x = -2, x \lt 0 \\ x = 2 \pm 2\sqrt<2>, x \gt 0 \end \right. \Rightarrow \left[ \begin x_1 = -2 \\ x_2 = 2 \pm 2\sqrt <2>\end \right. $$