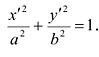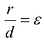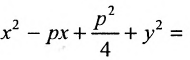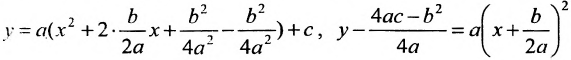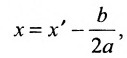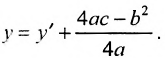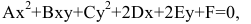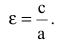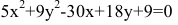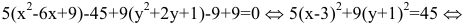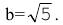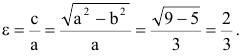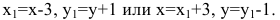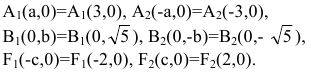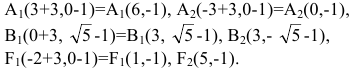3.1. Алгебраическая линия и её порядок
И сразу разбираемся в терминах:
Линию на плоскости называют алгебраической, если в аффинной системе координат её уравнение имеет вид 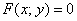
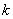
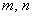
Как видите, уравнение алгебраической линии не содержит синусов, косинусов, логарифмов и прочего функционального бомонда. Только «иксы» и «игреки» в целых неотрицательных степенях (т.е. корней и переменных в знаменателе тоже нет).
Порядок линии равен максимальному значению 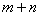
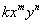
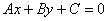
– слагаемое 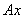
– слагаемое 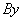
– в слагаемом 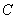
Максимальное значение равно 1, и поэтому прямая – это линия первого порядка.
Общее уравнение линии второго порядка имеет вид: 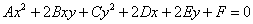
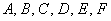
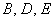
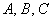
Почему порядок этой линии равен двум?
– слагаемое 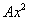
– у слагаемого 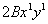
– слагаемое 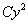
– все остальные слагаемые – меньшей степени.
Максимальное значение 2, и поэтому порядок линии равен двум.
Если к этому уравнению дополнительно приплюсовать, скажем, 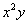
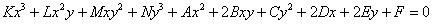
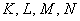
В том случае, если добавить одно или несколько слагаемых, которые содержат 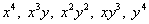
С алгебраическими линиями 3-го, 4-го и более высоких порядков нам придется столкнуться ещё не раз, в частности, при знакомстве с полярной системой координат. Ну а пока осваиваем порядок второй. Далее под словом «линия» по умолчанию будет подразумеваться алгебраическая линия на плоскости, и для простоты будем считать, что все события происходят в декартовой системе координат 
Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 
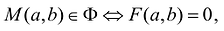
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
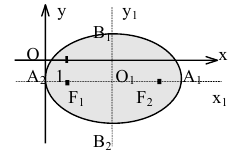
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 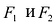
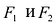
Точки 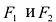
Если а =Ь, то уравнение (7.3) можно переписать в виде:
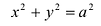
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 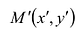
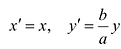
Число 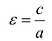
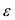
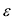
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 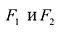
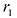
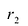
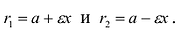
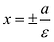
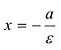
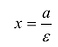
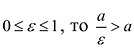
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 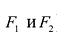
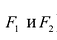
Точки 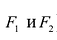
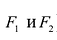
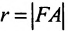
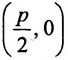
Тогда 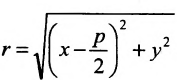
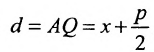
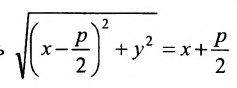
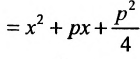
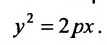
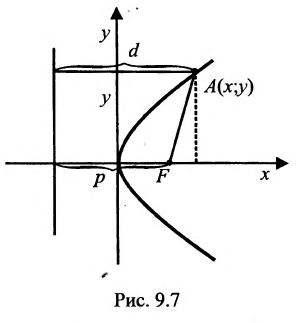
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 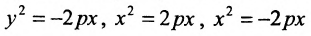
Легко показать, что уравнение 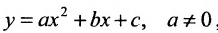
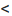
и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 
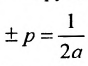
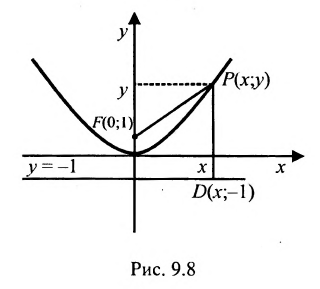
Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию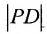
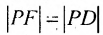
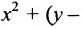
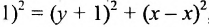
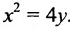
Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
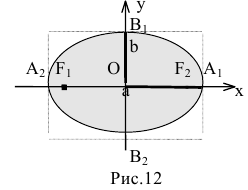
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
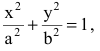
Число а называют большей полуосью эллипса, число 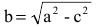
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 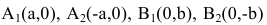
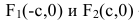
Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 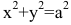
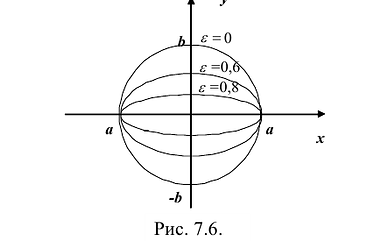
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 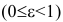
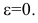
Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
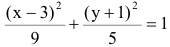
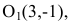
Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 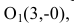
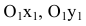
В новой системе координат координаты 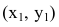
Переходя к старым координатам, получим:
Построим график эллипса.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Алгебраические уравнения линий на плоскости
Напомним, что многочленом степени одной переменной называется выражение вида
где — действительные числа (коэффициенты многочлена), — старший коэффициент, — свободный член. Степень многочлена обозначается .
Многочленом двух переменных называется выражение вида
где — действительные числа (коэффициенты многочлена), и — целые неотрицательные числа. Число
называется степенью многочлена двух переменных.
Алгебраической линией на плоскости называется множество точек, которое в какой-либо аффинной системе координат может быть задано уравнением вида
где — многочлен двух переменных и .
Уравнение вида (3.4) называется алгебраическим уравнением с двумя неизвестными. Степенью уравнения (3.4) называется степень многочлена . Одна и та же линия может быть задана уравнением вида (3.4) с многочленами разных степеней. Порядком алгебраической линии называется наименьшая из степеней этих многочленов.
Всякую неалгебраическую линию называют трансцендентной.
В примере 3.1,а,б,в,г,е — линии алгебраические: а — первого порядка, б,в,г,е — второго порядка. Примером трансцендентной линии служит синусоида, т.е. график функции . Эту линию нельзя задать уравнением вида (3.4).
Теорема (3.1) об инвариантности порядка алгебраической линии
Если в некоторой аффинной системе координат на плоскости линия задана уравнением (3.4), то и в любой другой аффинной системе координат эта линия задается уравнением того же вида (3.4) и той оке степени.
Действительно, пусть в аффинной системе координат уравнение имеет вид (3.4):
Получим уравнение этой линии в другой (новой) аффинной системе координат . Старые координаты точки связаны с новыми ее координатами выражениями (2.8):
где — координаты вектора переноса начала координат , а — элементы матрицы перехода базиса к новому . Подставим эти выражения в одночлен :
Раскрывая скобки, получаем многочлен двух переменных , степень которого не больше, чем . Аналогичные многочлены получим из других одночленов, входящих в левую часть (3.4). Сложив эти многочлены, получим многочлен , степень которого не превосходит степени исходного многочлена . Таким образом, при замене системы координат порядок алгебраической линии не увеличивается. Но он не может и уменьшиться, так как если порядок уменьшится при переходе к новой системе координат, то он должен увеличиться при обратном переходе к старой системе координат. Следовательно, порядок алгебраической линии остается неизменным в любой аффинной системе координат (говорят, что порядок алгебраической линии является инвариантом). Теорема доказана.
В аналитической геометрии на плоскости изучаются:
– алгебраические линии первого порядка, описываемые алгебраическим уравнением первой степени с двумя неизвестными:
– алгебраические линии второго порядка, описываемые алгебраическим уравнением второй степени с двумя неизвестными:
1. Теорема 3.1 фактически выражает свойство многочленов: при линейной невырожденной замене переменных
где , степень многочлена не изменяется.
Действительно, преобразование уравнения при переходе от одной системы координат к другой соответствует линейной невырожденной замене переменных многочлена в левой части уравнения.
2. Алгебраическое уравнение (3.4) может не иметь действительных решений. Например, на плоскости нет точек, координаты которых удовлетворяют уравнению . Однако в области комплексных чисел, согласно основной теоремы алгебры, любое алгебраическое уравнение имеет решения. Поэтому каждое алгебраическое уравнение (3.4) , где и , задает некоторую алгебраическую линию на двумерной комплексной плоскости (см. пункт 2 замечаний 2.9). Если все точки этой линии вещественные (действительные), т.е. , а , то линию называют вещественной (действительной). В противном случае линию называют мнимой.
3. Алгебраическими неравенствами с двумя неизвестными называются неравенства вида
где — многочлен двух переменных и . Степенью алгебраического неравенства называется степень многочлена .
4. Многочлены первой степени и алгебраические уравнения (неравенства) первой степени называются линейными.
5. Многочлен второй степени
называется также квадратичной функцией двух переменных; многочлен называется квадратичной формой (квадратичной частью функции), многочлен — линейной формой (линейной частью функции), коэффициент — свободным членом. По сравнению со стандартной записью многочлена некоторые коэффициенты квадратичной функции удвоены для удобства выполнения алгебраических преобразований.
6. Квадратичную функцию можно записать:
где — матрица квадратичной функции; расширенный (дополненный единицей)
столбец переменных;
б) выделяя квадратичную и линейную части:
7. Многочлены второй степени и алгебраические уравнения (неравенства) второй степени называются квадратичными (квадратными).
8. Линии, задаваемые системой алгебраических уравнений и неравенств, называются полуалгебраическими. Например, уравнение задает на координатной плоскости полуалгебраическую линию:
9. Теорема 3.1, разумеется, справедлива для прямоугольных систем координат на плоскости. Напомним, что преобразования прямоугольных систем координат являются ортогональными (см. пункт замечаний 2.3). Поэтому соответствующие этим преобразованиям линейные замены переменных (см. пункт 1) с ортогональной матрицей называются ортогональными (неоднородными при или однородными при ). Далее, как правило, будут рассматриваться уравнения, записанные в прямоугольной системе координат .
http://www.evkova.org/krivyie-vtorogo-poryadka
http://mathhelpplanet.com/static.php?p=algebraicheskie-uravneniya-linii-na-ploskosti