Алгебраических уравнений и систем моделирования

Основы математического моделирования систем и процессов (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

В каждом из перечисленных случаев в различной степени сказывается влияние таких ранее не учтенных факторов, как сила сопротивления воздуха, притяжение Луны, Солнца, убывание плотности атмосферы с высотой, вращение Земли, ветер, по-разному дующий на разных высотах, фактическое отличие формы Земли от шара (она является телом более сложной геометрической формы).

Проблема 3. Определение уровня детализации исследуемого объекта.

Любая физическая система представляет собой совокупность элементов. Каждый элемент в свою очередь можно расчленить на подэлементы. Процесс расчленения теоретически может быть бесконечным. Задача исследователя – выбрать оптимальный уровень детализации моделируемого объекта. Уровень детализации определяется целью моделирования и степенью знаний о свойствах элементов объекта.

Детализацию целесообразно производить до такого уровня, на котором для каждого элемента можно определить зависимость параметров выходных сигналов от параметров входных сигналов. Стремление повысить уровень детализации приводит к чрезмерной громоздкости модели и резкому увеличению ее размерности.

3-й этап. Формирование математической модели, т. е. запись модели в формализованном виде:

– все соотношения записывают в аналитической форме;

– логические условия выражают в виде систем неравенств;

– случайные процессы заменяют их типовыми моделями.

4-й этап. Исследование математической модели. Инструментами исследования являются численные и аналитические методы.

5-й этап. Анализ результатов моделирования с последующим выводом об адекватности модели либо о необходимости ее доработки, либо о ее непригодности.

1.3.4. Классификация математических моделей

Математические модели можно классифицировать по форме их представления (рис. 1.10). За основу второй классификации (рис. 1.11) взят характер модели.

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ФОРМЕ

СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

2.1. Области применения

Исследование некоторых физических систем приводит к математическим моделям в форме систем линейных алгебраических уравнений (СЛАУ). Иногда СЛАУ появляются в процессе математического моделирования как промежуточный шаг (этап) в решении более сложной задачи. Есть значительное число научно-технических задач, в которых математические модели сложных нелинейных систем посредством дискретизации или линеаризации сводятся к решению СЛАУ.

Примеры задач, использующих математические модели в форме СЛАУ:

1) при проектировании и эксплуатации электротехнических устройств требуется проведение расчета и анализа их работы в стационарных режимах. Задача сводится к расчету эквивалентных схем, в основе которого лежит формирование и решение СЛАУ;

2) при построении математической модели, связывающей функциональной зависимостью некоторые параметры x, y исследуемого объекта на основании полученных в результате эксперимента данных , где i = 1,2,3, . ,n (задачи аппроксимации данных);

3) при исследовании процессов в системах, математические модели которых строятся в классе дифференциальных уравнений в частных производных. В результате разностной аппроксимации исходной модели при определенных условиях приходят к математическим соотношениям в форме СЛАУ;

4) сущность многих физических процессов математически отображается с помощью интегральных уравнений. Ввиду сложности решения многих из них исследователь предпочитает свести задачу к решению модели в форме СЛАУ, используя известные методы аппроксимации.

5) исследование систем автоматического регулирования в установившемся режиме приводит во многих случаях к статическим моделям в форме СЛАУ.

Система линейных уравнений порядка n имеет вид:

(2.1)

или в векторно-матричной форме:

(2.2)

где – вектор свободных членов;

– вектор неизвестных;

A – матрица коэффициентов системы, размером .

2.2. Методы решения

Методы решения СЛАУ делятся на две группы: прямые (точные) и итерационные (приближенные).

Прямые методы позволяют получить решение за конечное число шагов. Итерационные методы построены по принципу многократного вычисления последовательных приближений, сходящихся к искомому решению.

Прямые методы целесообразно использовать для решения систем сравнительно небольшой размерности с плотно заполненной матрицей (матрицей, имеющей малое количество нулевых элементов). Итерационные методы предпочтительнее в задачах большой размерности со слабо заполненными матрицами.

К прямым методам относятся метод определителей, метод Гаусса и его модификации, метод LU-разложения, матричный метод и др. К разряду итерационных методов принадлежат метод простой итерации, метод Зейделя.

2.2.1. Прямые методы

2.2.1.1. Метод Гаусса

Решение СЛАУ осуществляется в два этапа (прямой и обратный ход)

Прямой ход. Исходная система (2.1) путем последовательных преобразований приводится к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений. В результате получается эквивалентная система:

(2.3)

Обратный ход. С помощью подстановки в предпоследнее (n-1)-е уравнение системы (2.3) вычисляется . Подстановкой и в (n-2)-е уравнение определяют . Таким же образом последовательно определяют неизвестные .

П р и м е р 14. Решить систему с тремя неизвестными методом Гаусса:

(2.4)

Прямой ход. Первое уравнение из системы (2.4) разделим на 3:

(2.5)

Из второго уравнения исключим неизвестное Для этого ко второму уравнению прибавим преобразованное первое уравнение, умноженное на (–2). Получим:

(2.6)

(2.7)

Разделим уравнение (2.7) на . Получим:

. (2.8)

Из третьего уравнения системы (2.4) исключим . Для этого из третьего уравнения вычтем первое преобразованное (2.5):

(2.9)

(2.10)

Разделим уравнение (2.10) на :

, (2.11)

(2.12)

Из третьего уравнения системы (2.12) исключим неизвестное . Для этого к третьему уравнению прибавим второе:

(2.13)

или , (2.14)

откуда выразим : .

Тогда эквивалентная система в треугольном виде примет вид:

(2.15)

Обратный ход. Подставим значение во второе уравнение системы (2.15) и найдем . Подстановкой значений и в первое уравнение найдем .

Если квадратная матрица линейной системы

(2.16)

имеет отличные от нуля главные диагональные миноры, т. е.

(2.17)

то она может быть разложена на произведение двух треугольных матриц – нижней с ненулевыми диагональными элементами и верхней – с единичными диагональными элементами

(2.18)

Поэтому матричное уравнение (2.16) можно заменить уравнением:

(2.19)

Введем вектор вспомогательных переменных Тогда уравнение (2.19) можно записать в виде системы двух векторно-матричных уравнений:

(2.20)

Таким образом, решение системы (2.16) сводится к последовательному решению двух систем с треугольными матрицами типа (2.3) или (2.15), из которых неизвестные определяются последовательной подстановкой.

Математически это выражается так: из первого уравнения системы (2.20) определяется вектор :

, (2.21)

после чего из второго уравнения системы (2.19) вычисляется вектор :

. (2.22)

Обратные матрицы и существуют, т. к. определители треугольных матриц L и U, вычисляемые как произведения их диагональных элементов, отличны от нуля.

Метод LU-разложения – это фактически метод Гаусса, выраженный в векторно-матричной форме, отличающийся от классического варианта способом хранения матриц.

2.2.1.3. Матричный метод

Если для системы выполняется условие невырожденности матрицы A

, (2.23)

то решение этой системы можно представить в виде:

, (2.24)

где – обратная матрица.

2.2.2. Итерационные методы

2.2.2.1. Метод простых итераций

Исходная система уравнений (2.1) приводится к виду:

(2.25)

(2.26)

Задав начальные (нулевые) приближения для искомых неизвестных:

(2.27)

подставляем их в правую часть системы (2.26). Получаемые при этом в левой части системы значения представляют собой первые приближения:

, (2.28)

где

Подставив первые приближения в правую часть системы (2.26), в левой ее части получим вторые приближения − :

. (2.29)

Таким образом, итерационный процесс описывается соотношениями:

(2.30)

Полученные в результате последовательности итераций приближения: сходятся к истинному решению системы (2.1), в том случае, если для коэффициентов системы (2.26) выполняется хотя бы одно из условий:

; (2.31)

. (2.32)

Вычисления продолжают до тех пор, пока не будет выполнено условие:

(2.33)

где – заданная точность.

2.2.2.2. Метод Зейделя

Метод Зейделя – модификация метода простых итераций, обеспечивающая ускорение сходимости итерационного процесса к истинному решению системы за счет следующего приема.

Уточненное значение , полученное из первого уравнения системы (2.26) вводится во второе уравнение системы и используется для вычисления . Затем уточненные значения , вводятся в третье уравнение системы (2.26) и используются для вычисления . Таким образом, k-е приближение будет определяться через уточненные в процессе k-й итерации значения . Следовательно, итерационный процесс, реализуемый в методе Зейделя, может быть выражен соотношениями:

(2.34)

3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ФОРМЕ НЕЛИНЕЙНЫХ

АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ

3.1. Пример формирования модели

П р и м е р 15. Моделируемый объект – нелинейная цепь постоянного тока (рис. 3.1). R2 – нелинейное сопротивление.

По закону Кирхгофа

(3.1)

Нелинейную вольт-амперную характеристику (ВАХ) элемента R2 аппроксимируем выражением:

(3.2)

Сделаем подстановку выражения (3.2) в уравнение (3.1):

(3.3)

(3.4)

f(i)

Соотношение f(i) = 0 представляет собой математическую модель электрической цепи в форме нелинейного алгебраического уравнения относительно тока i. Решение этой модели позволит определить ток i в цепи при заданных значениях U и R1.

Исследование объектов различной физической природы в установившемся режиме часто приводит к статическим моделям в форме нелинейных алгебраических уравнений.

Алгебраическое уравнение может содержать только алгебраические функции, в которых над переменной x производятся арифметические операции, возведение в степень с рациональным показателем и извлечение корня. Например:

(3.5)

(3.6)

В некоторых задачах моделирование приводит к трансцендентному уравнению.

Трансцендентным называется уравнение, в состав которого входят трансцендентные функции: показательная, логарифмическая, тригонометрические функции, возведение в иррациональную степень. Например:

(3.7)

(3.8)

3.2. Базовые понятия

Уравнение с одним неизвестным x в общем случае имеет вид:

где z(x) и g(x) — функции, определенные на некотором числовом множестве X, называемом областью допустимых значений уравнения.

Другая форма записи уравнения с одним неизвестным имеет вид:

где f(x) = z(x) – g(x) получается в результате переноса функции g(x) в левую часть уравнения (3.9).

Всякое значение x*, которое при подстановке в уравнение (3.10) обращает его в числовое равенство, а функцию f(x) — в ноль, т. е. такое, что

, (3.11)

называется корнем уравнения, или нулем функции f(x).

Решить уравнение – значит найти все его корни (решения) или доказать, что уравнение не имеет корней.

Для алгебраических уравнений число корней известно заранее. Каждое алгебраическое уравнение степени n имеет в множестве комплексных чисел n корней с учетом кратности.

3.3. Методы решения

Аналитическое (явное) решение, т. е. решение в виде готовой формулы, выражающей неизвестное x через параметры уравнения, можно получить только для ограниченного круга уравнений, например формулы для вычисления корней квадратного (аx2+bx+c=0) и кубического (x3+px+q=0) уравнений. Решение некоторых простейших трансцендентных уравнений может быть получено в аналитической форме с использованием степенных рядов, непрерывных дробей и т. д.

В большинстве случаев найти явное решение уравнения очень сложно или невозможно. Кроме того, использование аналитических формул для решения большинства уравнений не может обеспечить получение точного значения корня, поскольку коэффициенты уравнения являются приближенными величинами, определенными в результате измерений. Поэтому задача отыскания точного значения корня теряет смысл.

Ставится задача – определить приближенное значение корня уравнения с заданной точностью.

Приближенное решение математических задач лежит в основе численных методов.

3.3.1. Особенности численных методов решения

3.3.1.1. Этапы численного решения нелинейного уравнения

Численное решение уравнения f(x) = 0 (речь идет о действительных корнях) проводят в два этапа:

1) отделение корней, т. е. отыскание таких достаточно малых отрезков в области допустимых значений x, в которых содержится только один корень;

2) уточнение корней, т. е. вычисление корней с заданной точностью.

3.3.1.2. Отделение корней

Рассмотрим несколько способов отделения корней.

С п о с о б 1 – по графику функции y = f(x).

приближенно определяется как абсцисса точки пересечения графика с осью Оx (рис. 3.2). Устанавливаются границы a и b отрезка, в пределах которого заключен только один корень x*.

С п о с о б 2 – уравнение f(x) = 0 заменяют равносильным:

. (3.13)

Строят графики функций и

Приближенное значение корня определяют как абсциссу точки пересечения этих графиков.

Например: отделим корень уравнения

(3.14)

для области значений аргумента x > 0.

Преобразуем уравнение (3.14) к виду:

(3.15)

где

Строим графики (рис. 3.3) и находим приближенно x* и отрезок .

С п о с о б 3 – по таблице значений функции f(x) на интересующем интервале изменения аргумента x. Например, представим таблицу (табл.3.1) значений функции

. (3.16)

Из данных табл. 3.1 видно, что корень уравнения существует и его следует искать на отрезке [7,0; 10,0], так как значения функции на концах этого отрезка имеют разные знаки.

Таблица значений функции

С п о с о б 4 – аналитический метод отделения корней, который базируется на знании следующих свойств функции:

а) если функция непрерывна на отрезке и принимает на концах этого отрезка значения разных знаков, то внутри отрезка существует по крайней мере один корень уравнения ;

б) если функция непрерывна и монотонна на отрезке и принимает на концах отрезка значения разных знаков, а производная сохраняет постоянный знак внутри отрезка, то внутри этого отрезка существует корень уравнения и притом единственный.

Функция называется монотонной в заданном интервале, если при любых из этого интервала она удовлетворяет условию (монотонно возрастающая функция)

или (монотонно убывающая функция).

Необходимым и достаточным условием монотонности функции в заданном интервале является выполнение для всех внутренних точек этого интервала условия или

Зная свойства функции , можно сделать вывод о характере графика , что может существенно облегчить процесс отыскания корней. Продемонстрируем это для непрерывной и монотонной на отрезке функции , которая принимает на концах отрезка значения разных знаков, имеет во всех точках интервала первую и вторую производные и , сохраняющие постоянный знак (рис. 3.4).

3.3.1.3. Уточнение корней

Рассмотрим несколько численных методов уточнения корней, применяемых для решения как алгебраических, так и трансцендентных уравнений. Эти методы относятся к разряду итерационных.

Итерационный процесс состоит в последовательном шаг за шагом уточнении начального приближения x0 искомого корня. Каждый шаг такого метода называется итерацией.

В результате реализации итерационного метода получают последовательность приближенных значений корня Если эти значения с увеличением n приближаются к истинному значению корня x*, то говорят, что итерационный процесс сходится.

3.3.1.3.1. Метод половинного деления (дихотомии, бисекции)

Пусть дано уравнение

(3.17)

где функция непрерывна и монотонна на отрезке и имеет на концах отрезка разные знаки:

(3.18)

Требуется найти корень уравнения (3.17) с точностью до График функции представлен на рис. 3.5.

Рассмотрим суть и этапы реализации метода половинного деления.

1) Отрезок делим пополам и определяем середину отрезка:

(3.19)

2) Вычисляем значение функции в точке Если , то является корнем уравнения. Если то поиск корня продолжается на одном из двух полученных отрезков – или . Следует выбрать тот отрезок, на концах которого функция принимает значения противоположных знаков. В данном случае (см. рис. 3.5) выбираем отрезок , так как для него выполняется условие: Для того чтобы сохранить в дальнейших расчетах единое обозначение текущего отрезка, на котором ведется поиск корня на данном шаге вычислений, необходимо параметру b присвоить новое значение : b = . С точки зрения геометрической интерпретации (см. рис. 3.5) это означает, что правая граница исходного отрезка точка b переносится в точку а оставшаяся за пределами точки часть графика дальше не рассматривается.

Решение системы линейных алгебраических уравнений в параметрическом моделировании

Р.М.Ганеев, А.О.Максименко, А.В.Крючков

Система КОМПАС 3D предназначена для создания моделей (деталей и сборок) и графических документов. Параметрическое моделирование — неотъемлемая часть КОМПАС 3D (как и всех современных CAD/CAM-систем), позволяющая быстро получать модели типовых изделий на основе прототипа.

Особенностью системы КОМПАС 3D является использование собственного математического ядра и параметрических технологий.

В этой статье рассматривается построение параметрического дву­мерного эскиза или чертежа. При этом параметрическая модель состоит из развитого набора геометрических и алгебраических ограничений, заданных на конечном множестве геометрических объектов и переменных. Наиболее распространены такие объекты, как точки, отрезки, ­окружности и дуги окружностей. А параметрические зависимости описываются с помощью таких геометрических ограничений, как параллельность, перпендикулярность, совпадение, касание, линейные и угловые размеры и прочие отношения. Задачей параметризации в таком случае является решение, благодаря которому все геометрические объекты эскиза (чертежа) приводятся в состояние, удовлетворяющее заданным ограничениям.

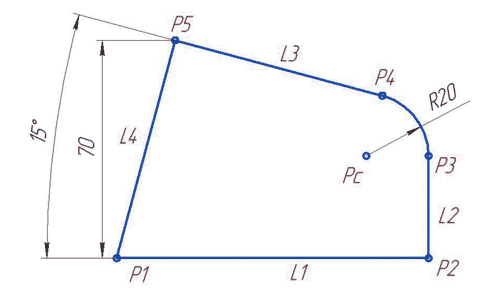
На рис. 1 представлен пример параметрического эскиза.

Рис. 1. Пример недоопределенной параметрической модели

Изображение на этом рисунке состоит из четырех прямых, шести точек, одной переменной и описывается системой из 20 ограничений:

где dispp (P1, P2, V) — расстояние на величину V между точками P1 и P2, displ (P, L, V ) — расстояние от точки P до прямой L, fix (P, c) фиксация координаты c у точки P, ang (L1, L2, V) — угол V между прямыми L1, L2, fix (V,const) — присвоение переменной V=const, hor (L) — горизонтальность прямой.

Каждое из ограничений убирает одну степень свободы объекта. С учетом того, что степень свободы точки и прямой равна 2, а переменной — равна 1, вся модель описывается 4*2 + 6*2 + 1 = 21 координатой степеней свобод. Таким образом, недостает ровно одного ограничения, чтобы полностью зафиксировать все объекты модели. Например, точки P2, P3, P4, Pc и прямая L2 имеют одну степень свободы перемещения, и в целом модель недоопределена.

Существуют различные подходы и методы решения задачи параметризации, и все они в основном подразделяются на методы, основанные на графах, на алгебраические и на численные:

• методы, основанные на графах, используют отвлеченную от геометрии эскиза информацию о структуре системы ограничений, например, для разбиения сложной в целом модели на более простые сепаратно решаемые подсистемы;

• алгебраические методы применяют к подсистемам, которые могут быть решены в аналитическом виде;

• численные методы хотя и проигрывают алгебраическим в эффективности, применяются в том случае, если ни один из альтернативных подходов не позволяет решить общую задачу.

Программное средство в составе CAD-системы, которое обеспечивает решение задач параметризации, как правило, применяет все описанные подходы в совокупности.

Для получения численного решения используют итерационные методы, которые, как известно, предполагают некоторое начальное приближение решения системы нелинейных уравнений. Оно уточняется на каждом шаге (итерации), пока не будет достигнута требуемая точность. Широко известный метод Ньютона-Рафсона на каждой итерации отыскивает решение системы линейных алгебраических уравнений (СЛАУ) согласно его итерационной формуле:

(1)

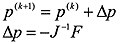
где k — номер итерации, pk — вектор решения на k-й итерации, Dp — вектор направления поиска решения, F — вектор значений функций, составляющих правую часть системы нелинейных уравнений, J — матрица Якоби 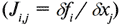, состоящая из частных производных 1-го порядка.

Для привлечения метода Ньютона к решению параметрической модели последняя формулируется в виде системы нелинейных алгебраических уравнений F(p) = 0 из функций в (1) .

Особенность параметрического моделирования состоит в том, что в общем случае система уравнений недоопределена, то есть количество неизвестных превышает количество уравнений. Кроме того, матрица J на некоторой итерации, в том числе и при начальном приближении, может оказаться вырожденной или близкой к таковой, что создает дополнительные трудности применения метода Ньютона.

Согласно (1), на каждом шаге итерационного процесса мы сталкиваемся с решением СЛАУ

(2)

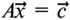
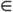
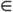
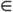
где A Rm,n, m — количество строк матрицы (количество уравнений), n — количество неизвестных, вектор правых частей c Rm , вектор неизвестных x R .

Вектор x определяет величину 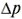в (1). В общем случае rank(A) 20,21 . Как оказалось, матрица имеет неполный ранг (rank(A)=18) по причине того, что в СЛАУ присутствуют два уравнения, векторы-строки которых образуют линейную комбинацию с другими уравнениями. В итоге СЛАУ в этом примере имеет бесчисленное множество решений, удовлетворяющих условию минимума

Для обеспечения сходимости процесса (1) в этом множестве выбирают вектор минимальной длины (нормальное решение). Известные алгоритмы решения недоопределенных СЛАУ [1, 2] не учитывают разреженную структуру больших матриц и, как следствие, обладают малой скоростью.

Р.М.Ганеев для повышения скорости решения предложил строить нормальное решение на базе предварительного приведения СЛАУ к треугольной форме.

Пусть ранг матрицы СЛАУ (2) меньше количества неизвестных. Для приведения СЛАУ (2) к треугольной форме используются методы отражений Хаусхолдера или отражений/вращений Гивенса. В случае СЛАУ с разреженной матрицей более эффективны методы Гивенса.

Пусть после приведения к треугольной форме получена совместная СЛАУ:

где R — правая треугольная n*n -матрица. При этом считаем, что i -е уравнение отсутствует, то есть в матрице R в i-й строке находятся только нули, и в векторе правой части i-й элемент равен нулю. Таких уравнений может быть несколько.

Коэффициенты дополнительного i -го уравнения вычисляются по формулам:

(4)

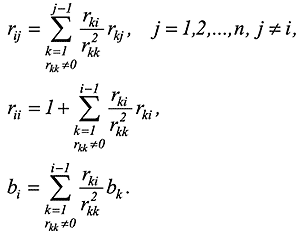
Общий алгоритм решения СЛАУ (2) содержит следующие шаги:

1. Параметры СЛАУ (2) необходимо записать в расширенную матрицу: R = [ A Ю ].

Матрица R должна содержать не менее n строк. Если количество уравнений m меньше количества неизвестных (m

Реферат по имитационному моделированию на тему «Эффективные алгоритмы численного решения алгебраических уравнений, расчета производных, решение систем линейных алгебраических и дифференциальных уравнений в Scilab.»

ФБГОУВПО «Мордовский Государственный педагогический институт им. М.Е.Евсевьева»

Кафедра информатики и вычислительной техники

Эффективные алгоритмы численного решения

алгебраических уравнений, расчета производных, решение

систем линейных алгебраических и дифференциальных

уравнений в Scilab.

Выполнил: студент группы МДМ-115

Проверила: Кормилицына Т.В.

Scilab ( /ˈsaɪlæb/ ) — пакет прикладных математических программ, предоставляющий открытое окружение для инженерных (технических) и научных расчётов. Это самая полная общедоступная альтернатива MATLAB.

С 1994 года распространяется вместе с исходным кодом через Интернет. В 2003 году для поддержки Scilab был создан консорциум Scilab Consortium. Сейчас в него входят 25 участников, в том числе Mandriva, INRIA и ENPC (Франция).

Scilab содержит сотни математических функций, и есть возможность добавления новых, написанных на различных языках (C, C++, Fortran и т. д.). Также имеются разнообразные структуры данных (списки, полиномы, рациональные функции, линейные системы), интерпретатор и язык высокого уровня.

Scilab был спроектирован как открытая система, и пользователи могут добавлять в него свои типы данных и операции путём перегрузки.

В системе доступно множество инструментов:

2D и 3D графики, анимация

Линейная алгебра, разреженные матрицы (sparse matrices)

Полиномиальные и рациональные функции

Симуляция: решение ОДУ и ДУ

Scicos: гибрид системы моделирования динамических систем и симуляции

Дифференциальные и не дифференциальные оптимизации

Scilab имеет схожий с MATLAB язык программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в Scilab.

Scilab позволяет работать с элементарными и большим числом специальных функций (Бесселя, Неймана, интегральные функции), имеет мощные средства работы с матрицами, полиномами (в том числе и символьно), производить численные вычисления (например, численное интегрирование) и решение задач линейной алгебры, оптимизации и симуляции, мощные статистические функции, а также средство для построения и работы с графиками.

Для численных расчётов используются библиотеки Lapack, LINPACK, ODEPACK , Atlas и другие.

В состав пакета также входит Scicos — инструмент для редактирования блочных диаграмм и симуляции (аналог simulink в пакете MATLAB). Имеется возможность совместной работы Scilab с программой LabVIEW.

Программа доступна для различных операционных систем, включая Linux, Microsoft Windows и Mac OS X. Возможности Scilab могут быть расширены внешними программами и модулями, написанными на разных языках программирования. Программа имеет открытый исходный код, что позволяет как свободное коммерческое использование и распространение неизменённых версий, так и некоммерческое распространение измененных версий, которые должны включать в себя исходный код. Для коммерческого распространения измёненных версий необходимо согласование с INRIA.

Начиная с версии 5.0 программа распространяется под совместимой с GNU GPL 2 лицензией CeCILL.

Отличия от некоторых коммерческих программ:

Свободность (с версии 5.0).

Маленький размер — дистрибутив 4 версии занимал менее 20 МБ против более чем двухгигабайтного пакета MATLAB. Инсталлятор 5 версии (5.4.1) увеличился в объёме до 117 МБ.

Возможность запуска в консоли без использования графического интерфейса, в том числе в версии под Windows (в UNIX и Windows версиях MatLab-а эта возможность присутствует тоже). Это позволяет производить автоматизированные вычисления, есть пакетный режим.

1 . Решение алгебраических уравнений.

Любое уравнение P(x) = 0, где P(x) — это многочлен, отличный от нулевого, называется алгебраическим уравнением или полиномом. Всякое алгебраическое уравнение относительно x можно записать в виде a0x n+a1x n−1+· · ·+an−1x+an = 0, где a0 6= 0, n > 1 и ai — коэффициенты алгебраического уравнения n–й степени. Например, линейное уравнение это алгебраическое уравнение первой степени, квадратное — второй, кубическое — третьей и так далее. Решение алгебраического уравнения в Scilab состоит из двух этапов. Необхо- димо задать полином P(x) с помощью функции poly, а затем найти его корни, применив функцию roots. Итак, определение полиномов в Scilab осуществляет функция poly(a, «x [«fl»]),

Любое уравнение P(x) = 0, где P(x) — это многочлен, отличный от нулевого, называется алгебраическим уравнением или полиномом. Всякое алгебраическое уравнение относительно x можно записать в виде a0x n+a1x n−1+· · ·+an−1x+an = 0, где a0 6= 0, n > 1 и ai — коэффициенты алгебраического уравнения n–й степени. Например, линейное уравнение это алгебраическое уравнение первой степени, квадратное — второй, кубическое — третьей и так далее. Решение алгебраического уравнения в Scilab состоит из двух этапов. Необхо- димо задать полином P(x) с помощью функции poly, а затем найти его корни, применив функцию roots. Итак, определение полиномов в Scilab осуществляет функция

параметра a воспринимаются функцией как корни, для которых необходимо рас- считать коэффициенты соответствующего полинома. По умолчанию fl=r. Следующий пример отражает создание полинома p, имеющего в качестве корня тройку, и полинома f с коэффициентом 3.

Далее приведены примеры создания более сложных полиномов.

—>//Полином с корнями 1, 0 и 2

ans = 2 3 2x — 3x + x

—>//Полином с коэффициентами 1, 0 и 2

предназначена для решения алгебраического уравнения. Здесь p — это полином, созданный функцией poly и представляющий собой левую часть уравнения P(x) = 0.

Решим несколько алгебраических уравнений.

Найти корни полинома 2x 4 − 8x 3 + 8x 2 − 1 = 0.

Для решения этой задачи необходимо задать полином p. Сделаем это при по- мощи функции poly, предварительно определив вектор коэффициентов V . Обра- тите внимание, что в уравнении отсутствует переменная x в первой степени, это означает, что соответствующий коэффициент равен нулю:

p = 2 3 4 1 + 8x — 8x + 2x

Теперь найдем корни полинома:

2. Вычисление производной функции в точке. Приближенное вычисление частных производных .

Универсальной командой дифференцирования является команда

здесь fun — имя функции, задающей выражение для дифференцирования. Функция должна быть задана в виде y=fun(x [, p1, p2. pn]),

где x — переменная, по которой будет проводится дифференцирование. Если параметры p1, p2, . . . , pn присутствуют в описании функции, то они должны быть обязательно определены при вызове, например, так:

Результат работы функции — матрица gij = dfi /dxj .

Рассмотрим несколько примеров.

Вычислить f ′ (1), если f(x) = (x + 2)3 + 5x

—>function f=my(x), f=(x+2)^3+5*x, endfunction;

Задана функция многих переменных y(x1,x2,x3) = x1x x3 2 +x 2 1×3. Вычислить dy/dx1 , dy/dx2 , dy/dx3 в точке (1, 2, 3).

—>function [Y]=f(X), Y=X(1)*X(2)^X(3)+X(1)^2*X(3),endfunction

ans = 14. 12. 6.5451775

3. Решение систем линейных алгебраических уравнений.

Система m уравнений с n неизвестными вида:

a11x1 + a12x2 + · · · + a1nxn = b1 ,

a21x1 + a22x2 + · · · + a2nxn = b2,

am1x1 + am2x2 + · · · + amnxn = bm

называется системой линейных алгебраических уравнений (СЛАУ), причем xj — неизвестные, aij — коэффициенты при неизвестных, bi — свободные коэффициенты (i = 1 . m, j = 1 . n). Система из m линейных уравнений с n неизвестными может быть описана при помощи матриц:

A · x = b, где x — вектор неизвестных, A — матрица коэффициентов при неизвестных или матрица системы, b — вектор свободных членов системы или вектор правых частей. Совокупность всех решений системы (x1,x2. ,xn) называется множеством решений или просто решением системы.

Решить СЛАУ при помощи правила Крамера:

2×1 + x2 − 5×3 + x4 = 8 ,

x1 − 3×2 − 6×4 = 9 ,

2×2 − x3 + 2×4 = −5 ,

x1 + 4×2 − 7×3 + 6×4 = 0 .

Правило Крамера заключается в следующем. Если определитель ∆ = det A матрицы системы из n уравнений с n неизвестными A · x = b отличен от нуля, то система имеет единственное решение x1,x2. ,xn, определяемое по формулам Крамера: xi = ∆i/∆, где ∆i — определитель матрицы, полученной из матрицы системы A заменой i-го столбца столбцом свободных членов b. Текст файла- сценария с решением задачи по формулам Крамера: 54

A=[2 1 -5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6];

b=[8;9;-5;0]; //Вектор свободных коэффициентов

A1=A;A1(:,1)=b; //Первая вспомогательная матрица

A2=A;A2(:,2)=b; //Вторая вспомогательная матрица

A3=A;A3(:,3)=b; //Третья вспомогательная матрица

A4=A;A4(:,4)=b; //Четвертая вспомогательная матрица

D=det(A); //Главный определитель

//Определители вспомогательных матриц:

x = d / D //Вектор неизвестных

P = A * x — b //Проверка

Решим систему из двух уравнений вида A*x=b

Задаем матрицу коэффициентов:

Задаем вектор свободных коэффициентов:

Определяем детерминант матрицы:

Так как определитель матрицы отличен от нуля, решение СЛАУ существует.

Решение СЛАУ методом обратной матрицы

Запись A\b соответствует математической операции A -1 b. Записи x=A\b эквивалентна запись x=inv(A)*b

Эту систему уравнений также можно решить с помощью специальной функции linsolve (эта функция решает уравнение вида Ax+b=0, поэтому поменяем знак вектора b)

и получили ответ: x ₀ = -3; x ₁ = 2.5;

результирующий вектор близок к нулю, то есть система решена верно.

4. Решение обыкновенных дифференциальных уравнений

Дифференциальным уравнением n-го порядка называется соотношение вида

Решением дифференциального уравнения является функция x(t), которая обращает уравнение в тождество. Системой дифференциальных уравнений n-го порядка называется система вида:

x ′ 1 = f1(t,x1,x2. ,xn)

x ′ 2 = f2(t,x1,x2. ,xn)

x ′ n = fn(t,x1,x2. ,xn)

Решение системы — вектор, который обращает уравнения системы в тождества:

  Дифференциальные уравнения и системы имеют бесконечное множество ре шений, которые отличаются друг от друга константами. Для однозначного определения решения требуется задать дополнительные начальные или граничные условия. Количество таких условий должно совпадать с порядком дифференциального уравнения или системы. В зависимости от вида дополнительных условий в дифференциальных уравнениях различают: задачу Коши — все дополнительные условия заданы в одной (чаще начальной) точке интервала; краевую зада- чу — дополнительные условия указаны на границах интервала. Большое количество уравнений может быть решено точно. Однако есть уравнения, а особенно системы уравнений, для которых точное решение записать нельзя. Такие уравнения и системы решают при помощи численных методов. Численные методы также применяют в том случае, если для уравнений с из- вестным аналитическим решением требуется найти числовое значение при опре- деленных исходных данных. Для решения дифференциальных уравнений и систем в Scilab предусмотрена функция [y,w,iw]=ode([type],y0,t0,t [,rtol [,atol]],f [,jac] [,w,iw])

для которой обязательными входными параметрами являются: y0 — вектор на- чальных условий; t0 — начальная точка интервала интегрирования; t — коорди- наты узлов сетки, в которых происходит поиск решения; f — внешняя функция, определяющая правую часть уравнения или системы уравнений (8.2); y — вектор решений . Таким образом, для того чтобы решить обыкновенное дифференциаль- ное уравнение вида dy/dt = f(t,y), y(t0) = y0, необходимо вызвать функцию y=ode(y0,t0,t,f). Рассмотрим необязательные параметры функции ode: type — параметр, с помощью которого можно выбрать метод решения или тип решаемой задачи, указав одну из строк: adams — применяют при решении дифференциальных уравнений или систем методом прогноза-коррекции Адамса; stiff — указывают при решении жестких задач; rk — используют при решении дифференциальных уравнений или систем методом Рунге — Кутта четвертого порядка; rkf — указывают при выборе пятиэтапного метода Рунге — Кутта четвертого порядка; fix — тот же метод Рунге — Кутта, но с фиксированным шагом; rtol, atol — относительная и абсолютная погрешности вычислений, вектор, раз- мерность которого совпадает с размерностью вектора y, по умолчанию rtol=0.00001, atol=0.0000001, при использовании параметров rkf и fix — rtol=0.001, atol=0.0001; jac — матрица, представляющая собой якобиан правой части жесткой системы дифференциальных уравнений, задают матрицу в виде внешней функции вида J=jak(t,y); w, iw — векторы, предназначенные для сохранения информации о параметрах интегрирования, которые применяют для того, чтобы последующие вычис- ления выполнялись с теми же параметрами.

Решить задачу Коши x ′ = cos(xy), y ′ = sin(x + ty), x(0) = 0, y(0) = 0. на интервале [0; 10].

//Функция, описывающая систему дифференциальных уравнений