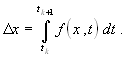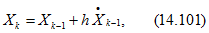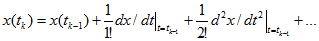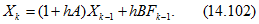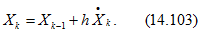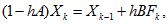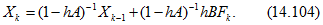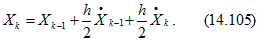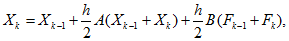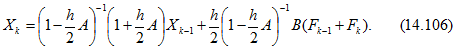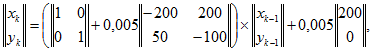Алгоритм эйлера для численного решения уравнения состояния

Алгоритм эйлера для численного решения уравнения состояния

18.1. РЕШЕНИЕ УРАВНЕНИЙ СОСТОЯНИЯ ЧИСЛЕННЫМИ МЕТОДАМИ

Для использования стандартных методов численного интегрирования обыкновенных дифференциальных уравнений интегрируемая система должна быть записана в нормальной форме

, .

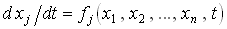
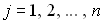
Здесь принята общая запись правой части уравнений состояния, охватывающая и нелинейные уравнения, так как рассматриваемые ниже методы пошагового интегрирования одинаковы для линейных и нелинейных уравнений. Именно к такой форме приводит метод переменных состояния. Его применение целесообразно и при формировании уравнений для численного интегрирования.

Основой используемых численных методов является вычисление приращений переменных состояния D x j за рассматриваемый промежуток времени — шаг интегрирования D t k = t k + 1 – t k = h

В последнем выражении индексы j у переменных x и f для упрощения записи опущены.

Методы численного интегрирования, известные из курса численного анализа, различаются по способу аппроксимации подынтегральной функции в последнем выражении. Наиболее простой вид имеют формулы

• явного метода Эйлера D x = f k (x k , t k )h = f k h;

• неявного метода Эйлера D x = f k+ 1 h;

• метода трапеций D x = (f k + f k+ 1 )h/2.

Поскольку и последнее выражение содержит значения f k +1 , не известные в начале вычислений на данном шаге, то метод трапеций также является неявным.

Реализация неявных методов требует на каждом шаге решения системы уравнений относительно неизвестных значений x k +1 в конце данного шага. Выбор шага интегрирования h связан с обеспечением точности и устойчивости численного решения. Обеспечение устойчивости является определяющим при интегрировании так называемых жестких систем дифференциальных уравнений, у которых корни характеристического уравнения резко различаются по модулю.

Пример расчета переходного процесса в цепи, рассмотренной в Задаче 14.1 путем численного интегрирования уравнений состояния рассмотрен в Задаче 14.3. Как следует из полученного решения, при принятом шаге интегрирования h = 10 — 5 с все три использованные метода обеспечивают достаточно высокую точность решения. В то же время при попытке увеличить шаг интегрирования до значения h = 8·10 — 4 с явный метод Эйлера теряет устойчивость, неявные же методы дают устойчивые результаты, хотя их точность ухудшается. В условиях рассмотренной задачи вопрос выбора подходящего метода интегрирования несущественен, так как точный результат обеспечивает любой из сопоставляемых методов за приемлемое число шагов, т.е. при разумных затратах машинного времени. Однако это имеет место не всегда. Так, при уменьшении индуктивности в рассматриваемой схеме (рис. П14.1) до значения L = 10 — 4 Гн предельный шаг интегрирования, выбираемый по условию устойчивости в явном методе Эйлера сокращается до значения h _м = 8·10 — 7 с. Поскольку общая длительность переходного процесса при таком уменьшении индуктивности сохраняется практически неизменной, то теперь для получения полной картины переходного процесса явным методом необходимо совершить 0,01/ h _м @ 12500 шагов. Очевидно, что для еще меньших значений индуктивности L в рассматриваемой задаче (что ведет к увеличению жесткости интегрируемой системы уравнений) подобное соотношение будет еще более невыгодным. Это характерно для решения жестких систем дифференциальных уравнений любым явным методом численного интегрирования. Дальше
Обратно к плану лекции

Алгоритмы численного решения уравнений состояния

Алгоритмы численного решения уравнений состояния

где [f₁ (t)] и [f₂ (t)] – матрицы воздействий и реакций; [A], [B] – матрицы коэффициентов.

1. Явная форма алгоритма Эйлера реализует на n-м шаге численного решения уравнение

которое, фактически, является разностным уравнением для дискретной цепи, поскольку f_n ≡ f (nT) – дискретная последовательность, а T – шаг численного интегрирования, то есть период (интервал) дискретизации; в уравнении «явной формы» справа записывают данные предыдущего шага f _(n–1) ≡ f (nT – T).

2. Неявная форма алгоритма Эйлера

то есть справа записывают данные рассматриваемого шага.

3. Смешанная форма алгоритма Эйлера

то есть справа «берут» воздействие на рассматриваемом шаге, а реакцию – на предыдущем.

4. Билинейное преобразование

[ f 2 n ] − [ f 2 ( n − 1 ) ] T = [ A ] ⋅ [ f 2 n ] − [ f 2 ( n − 1 ) ] 2 + [ B ] ⋅ [ f 1 n ] − [ f 1 ( n − 1 ) ] 2 ,

то есть справа записывают «средние», а слева – приращение реакции на рассматриваемом шаге численного интегрирования уравнений состояния.

Алгоритмы численного решения уравнений состояния, Явная форма алгоритма Эйлера, Неявная форма алгоритма Эйлера, Смешанная форма алгоритма Эйлера, Билинейное преобразование

Численные методы решения уравнений состояния

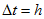
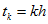
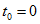
Интегрирование дифференциальных уравнений, составленных методом переменных состояния в форме Коши ( 14.91), чаще выполняется численными методами на ЭВМ с применением программ. Интервал времени, в течение которого необходимо найти значения искомых величин, разделяется на малые равные (или неравные) промежутки — шаги , и в результате расчета получаются значения этих величин в отдельные (дискретные) моменты времени , где k = 1, 2, 3. Предполагается, что значения искомых величин в начальный момент времени известны (начальные условия задачи).

Математиками разработаны различные методы численного решения уравнений, записанных в форме Коши, из которых далее рассматриваются более простые — одношаговые. В одношаговых методах искомые величины в момент времени 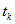определяются по уже найденным значениям на предыдущем одном шаге.

Наиболее простой из одношаговых методов — явный метод Эйлера или алгоритм Рунге-Кутта первого порядка — записывается так:

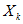
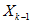
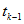
где матрица-столбец переменных состояния для k-го шага; Xk-t — то же для (к — 1)-го шага (в момент tk-1); — матрица-столбец производных (точнее, угловых коэффициентов касательных) переменных состояния в момент (в начале предыдущего шага). Метод основан на разложении каждой переменной состояния в ряд Тейлора

и учете его первых двух членов. Метод назван явным, так как искомое решение для k-го шага не входит в правую часть алгоритма (14.101), связывающего значения на последующем и предыдущем шагах.

После подстановки (14.916), записанного для (k — 1)-го шага, в (14.101) получим

Формула (14.102) — это рекуррентное соотношение, которое дает возможность непосредственно определять последующие значения переменных состояния по найденным на предыдущем шаге. Чем меньше шаг h, тем точнее расчет, но больше объем вычислений. Погрешность расчета пропорциональна .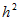

В алгоритмах Рунге-Кутта более высокого порядка искомые величины для k-го шага определяются с учетом их значений в нескольких промежуточных точках предыдущего (k — 1)-го шага, так что точность расчета увеличивается.

Если в правой части (14.101) производные для предыдущего (k — 1)-го шага заменить производными для данного k-го шага, то получим

Алгоритм называется неявным методом Эйлера, так как правая часть (14.103) содержит производные для того же шага, для которого определяются переменные состояния.

После подстановки ( 14.91 б), записанного для момента 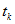, в (14.103) получим

Погрешность расчета того же порядка, что и для явного метода Эйлера.

Лучшую точность обеспечивает метод трапеций (относится к неявным), так как в правой части содержит средние значения производных (k — 1)-го и k-го шагов:

После подстановки (14.916), записанных для моментов 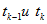, в (14.105) получим

Погрешность расчета пропорциональна .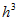

Полная погрешность зависит не только от выбранного метода расчета, т. е. от методической погрешности (алгоритмической), но и от погрешности округления из-за ограниченного количества разрядов цифровых значений величин, что относится, конечно, к любым расчетам электрических цепей.

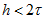
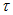
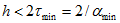
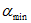
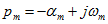
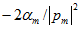
С ростом числа шагов погрешность интегрирования может увеличиваться, т. е. численное решение может давать значения, все более отличающиеся от истинных. В этом случае получается численно неустойчивый алгоритм, который нельзя использовать для расчета переходного процесса. Устойчивость явного метода Эйлера зависит от шага к Для цепей с одним накопителем алгоритм получается устойчивым при , где — постоянная времени цепи. Для цепи с несколькими накопителями при действительных корнях характеристического уравнения необходимо выбрать , где — минимальный коэффициент затухания, а при наличии и комплексных корней шаг h должен быть еще и меньше минимального значения .

Неявный метод Эйлера и метод трапеций устойчивы при любом шаге. Поэтому выбор шага диктуется только необходимой точностью расчета, которая, однако, при уже выбранном шаге еще неизвестна, что относится и к явным методам.

Для цепи примера 14.6 (рис. 14.42) сравнить результаты расчета тока 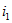явным методом Эйлера, неявным методом Эйлера и методом трапеций с данными аналитического расчета, приведенными в примере 14.6, при шаге h = 0,005 с.

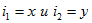
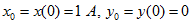
Решение. Обозначим переменные состояния , так что .

Явный метод Эйлера. Согласно (14.102)

и после выполнения операций сложения и умножения матриц получим