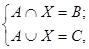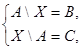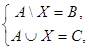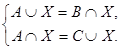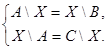Алгоритм решения систем уравнений в теории множеств

Решение некоторых задач по теории множеств

Разделы: Математика

На математическом кружке вместе с учащимися рассматривался ряд задач, благодаря наглядности которых, процесс решения становится понятным и интересным. На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.

Введем определение множества, а так же некоторые обозначения.

Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.

Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.

Можно сделать такую запись определения множества:

, где

“” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.

Два множества будем называть равными, если они состоят из одних и тех же элементов

Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если , то , где “С” знак подмножества или включения.

Графически это выглядит так (рис.1):

Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.

Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).

Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или ” ключевое в понимании элементов входящих в объединение множеств.

Это определение можно записать с помощью обозначений:

А υ В, где

где “ υ ” – знак объединения,

“ / ” – заменяет слова ”таких что“

Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:

А ∩ В = С, где

“∩“ – знак пересечения. (рис.3)

Обозначим буквой Е основное или универсальное множество, где A С Е (“”- любо число), т.е. А Е = Е; АЕ =А

Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается Ā Е или Ā (рис.4)

Е

Примерами для понимания этих понятий являются свойства:

А Ā=Е Ø = Е Е Ā=Ā

Свойства дополнения имеют свойства двойственности:

АВ = А∩В

АВ = АUВ

Введем еще одно понятие – это мощность множества.

Для конечного множества А через m (A) обозначим число элементов в множестве А.

Из определение следуют свойства:

Для любых конечных множеств справедливы так же утверждения:

m (AB) =m (A) + m (В) – m (А∩В)

m (A∩B) = m (A) + m (В) – m (АВ)

m (ABC) = m (A) + m (В) + m (С)– m (А∩В) — m (А∩С) – m (В∩С) – m (А∩В∩С).

А теперь рассмотрим ряд задач, которые удобно решать, используя графическую иллюстрацию.

Задача №1

В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек.

По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 9 человек. Ни одной задачи не решили 3 человека.

1. Сколько учащихся решили все задачи?
2. Сколько учащихся решили только две задачи?
3. Сколько учащихся решили только одну задачу?

Задача № 2

Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.

Сколько студентов успешно решили только одну контрольную работу?

Задача № 3

В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников.

Сколько учеников пользуются только одним видом транспорта?

Решение задачи № 1

Запишем коротко условие и покажем решение:

• m (Е) = 40
• m (А) = 20
• m (В) = 18
• m (С) = 18
• m (А∩В) = 7
• m (А∩С) = 8
• m (В∩С) = 9

m (АВС) = 3 => m (АВС) = 40 – 3 = 37

Обозначим разбиение универсального множества Е множествами А, В, С (рис.5).

К 1 – множество учеников, решивших только одну задачу по алгебре;

К 2 – множество учеников, решивших только две задачи по алгебре и геометрии;

К 3 – множество учеников, решивших только задачу по геометрии;

К 4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;

К 5 – множество всех учеников, решивших все три задачи;

К 6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;

К 7 – множество всех учеников, решивших только задачу по тригонометрии;

К 8 – множество всех учеников, не решивших ни одной задачи.

Используя свойство мощности множеств и рисунок можно выполнить вычисления:

• m (К 5 ) = m (А∩В∩С)= m (АВС) — m (А) — m (В) — m (С) + m (А∩В) + m (А∩С) + m (В∩С)
• m (К 5 ) = 37-20-18-18+7+8+9=5
• m (К 2 ) = m (А∩В) — m (К 5 ) = 7-5=2
• m (К 4 ) = m (А∩С) — m (К 5 ) = 8-5=3
• m (К 6 ) = m (В∩С) — m (К 5 ) = 9-5=4
• m (К 1 ) = m (А) — m (К 2 ) — m (К 4 ) — m (К 5 ) = 20-2-3-5=10
• m (К 3 ) = m (В) — m (К 2 ) — m (К 6 ) — m (К 5 ) = 18-2-4-5=7
• m (К 7 ) = m (С) — m (К4) — m (К 6 ) — m (К 5 ) = 18-3-4-5 =6
• m (К 2 ) + m (К 4 ) + m (К6) = 2+3+4=9 – число учеников решивших только две задачи;
• m (К 1 ) + m (К 3 ) + m (К 7 ) = 10+7+6=23 – число учеников решивших только одну задачу.

Ответ:

5 учеников решили три задачи;

9 учеников решили только по две задачи;

23 ученика решили только по одной задаче.

С помощью этого метода можно записать решения второй и третьей задачи так:

Решение задачи № 2

• m (АВ) = 33
• m (АС) = 31
• m (ВС) = 32
• m (К 2 ) + m (К 4 ) + m (К 6 ) + m (К 5 ) = 20

Найти m (К 1 ) + m (К 3 ) + m (К 7 )

• m (АUВ) = m (К 1 ) + m (К 2 ) + m (К 3 ) + m (К 4 ) + m (К 5 ) + m (К 6 ) = m (К 1 ) + m (К 3 ) + 20 = 33 =>
• m (К 1 ) + m (К 3 ) = 33 – 20 = 13
• m (АUС) = m (К 1 ) + m (К 4 ) + m (К 2 ) + m (К 5 ) + m (К 6 ) + m (К 7 ) = m (К 1 ) + m (К 7 ) + 20 = 31 =>
• m (К 1 ) + m (К 7 ) = 31 – 20 = 11
• m (ВUС) = m (К 3 ) + m (К 2 ) + m (К 5 ) + m (К 6 ) + m (К 7 ) + m (К 4 ) = m (К 3 ) + m (К 7 ) + 20 = 32 =>
• m (К 3 ) + m (К 7 ) = 32 – 20 = 12
• 2m (К 1 ) + m (К 3 ) + m (К 7 ) = 13+11=24
• 2m (К 1 ) + 12 = 24
• 
• m (К 3 )= 13-6=7
• m (К 7 )=12-7=5
• m (К 1 ) + m (К 3 ) + m (К 7 ) = 6+7+5=18

Ответ:

Только одну контрольную работу решили 18 учеников.

Решение задачи № 3

• m (Е) = 35
• m (А∩В∩С)= m (К 5 ) = 6
• m (А∩В)= 15
• m (А∩С)= 13
• m (В∩С)= 9

Найти m (К1) + m (К3) + m (К 7 )

• m (К 2 ) = m (А∩В) — m (К 5 ) = 15-6=9
• m (К 4 ) = m (А∩С) — m (К 5 ) = 13-6=7
• m (К 6 ) = m (В∩С) — m (К 5 ) = 9-6=3
• m (К 1 ) + m (К 3 ) + m (К 7 ) = m (Е) — m (К 4 ) — m (К 2 ) — m (К 6 ) — m (К 5 ) = 35-7-9-3-6=10

Ответ:

Только одним видом транспорта пользуется 10 учеников.

Литература: А.Х. Шахмейстер «Множества. Функции. Последовательности»

Уравнения и системы уравнений в алгебре множеств

Для формализации процесса решения уравнений и систем уравнений в алгебре множеств введем дополнительные определения.

Пусть J — универс и A(1),A(2). A(n) — заданные множества этого универса, X — неизвестное множество. Обозначим через F[A(1),A(2). A(n),X] и R[A(1),A(2). A(n),X] две формулы алгебры множеств. Множество X* называется частным решением уравнения

если F[A(1),A(2). A(n),X*] и R[A(1),A(2). A(n),X* ] определяют одно и то же множество.

Множество всех частных решений задает общее решениеуравнения (1).

Путем преобразования (используя законы алгебры множеств и следующие из них результаты) уравнение (1) может быть преобразовано к виду:

AX B C= . (2)

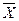
Пусть задана система уравнений в алгебре множеств. Путем эквивалентных преобразований система уравнений так же может быть преобразована к виду (2). Отсюда, для решения уравнения или системы уравнений в алгебре множеств, необходимо уметь находить общее решение уравнения типа (2).

Основные леммы, используемые при решении уравнений в алгебре множеств.

Для преобразования уравнений и систем уравнений в алгебре множеств к виду:

AX B C= , (1)

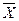
а так же для нахождения общего решения уравнения (1), используются следующие результаты, получающиеся из законов алгебры множеств.

Лемма 1.

AB тогда и только тогда, если A = .

Покажем, что из AB следует A = .

Доказательство от противного. Пусть AB, но A . Отсюда существует такой элемент а, который одновременно принадлежит и множеству А и множеству . Это означает, что этот элемент а принадлежит множеству А и не принадлежит множеству В, что противоречит условию AB.

Покажем, что из A = следует AB.

Доказательство от противного. Пусть A = , но множество А не является подмножеством В. Тогда множество А содержит такой элемент а, которого нет в множестве В. Отсюда этот элемент принадлежит и множеству А и множеству , что противоречит условию A .

Лемма 2.

А=В тогда и только тогда, если А В= .

Покажем, что из А=В следует А В= .

Если А=В, то А =А = и В =В = , отсюда А В= .

Покажем, что из А В= следует А=В.

Если А В= , то это значит что А = , т.е. по лемме 1 AB, и В = , т.е. по лемме 1 ВА, Получили одновременно АВ и В А, что соответствует А=В.

Лемма 3.

= , тогда и только тогда, если = , i=1,2. n.

Доказательство индукцией по n.

Лемма 4.

=J, тогда и только тогда, если =J, i=1,2. n.

Доказательство следует из леммы 3 на основании принципа двойственности.

Полученные теоретические результаты позволяют находить общее решение уравнений и систем уравнений.

относительно неизвестного множества X.

Из леммы 1 следует, что уравнение (1) эквивалентно уравнению

F[A(1),A(2). A(n),X] R[A(1),A(2). A(n),X]= . (2)

После преобразований (применив, если это надо, закон де Моргана и другие законы алгебры множеств; на основании ассоциативного и дистрибутивного законов раскрыв скобки и приведя подобные члены) уравнение (2) становится эквивалентным уравнению

AX B C= , (3)

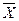
где А,В и С — некоторые множества, полученные в результате проведенных преобразований.

Из (3) по лемме 3 следует, что AX= , B = , C= .

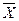
Из того, что AX= и B = , по лемме 1 следует:

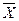
В X .

Отсюда, уравнение (3) эквивалентно условиям :

В X ,C= . (4)

Так как X произвольное множество из универса, то из (3) следует, что условия :

В ,C= (5)

являются необходимыми и достаточными для того, чтобы исходное уравнение (1) имело решение.

Вместо условий (5) можно пользоваться эквивалентными им (на основании лемм1 и 3) условиями :

АВ C= . (6)

Мы получили, что любое множество X* из универса, удовлетворяющее условиям (4), является частным решением уравнения (1).

Из условий (4) следует, что решение исходного уравнения (1) определяется следующим выражением:

X*= В К ,(7)

где К — произвольное множество универса.

Таким образом, мы получили, что при любом К из универса выражение (7) представляет собой частное решение исходного уравнения (1), т.е. (7) определяет общее решение исходного уравнения (1). Из выражения (7) следует и оценка числа решений уравнения (1) N= . Проверим полученное решение. Так как X* решение системы (1), то оно является и решением преобразованного уравнения (2). Подставив в уравнение (2) выражение для X* из (7), получим:

A(В К) B() C=AB B( ) C=AB C= .

Здесь последнее равенство следует из условий (6).

Замечание.

Так как система уравнений алгебры множеств может быть приведена на основании выше доказанных лемм к виду (3), то результаты, полученные для случая решения уравнения, справедливы и для случая решения системы уравнений.

Решение систем уравнений

Дата добавления: 2015-07-23 ; просмотров: 392 ; Нарушение авторских прав

1. Решить систему уравнений

где А, В, и С — данные множества, и В ÍА ÍС.

Используя тождества задач 1.2 и 1.3 предыдущего раздела, получим:

· А ÇХ =В Û А Ç Х ÍВ и В Í А Ç Х. Следовательно, из второго включения

В Í А, и В ÍХ; из первого включения : Х Í `А È В. Из этих двух

включений: В Í Х Í `А È В.

· А È Х = С Û А È Х Í С и С Í А È Х. Из первого включения следует,

что А Í СХ Í С, из второго включения имеем С Ç `А Í Х. Следовательно,

· Соединяя двойные включения, полученные из первого и второго уравнений,

получим (`А Ç С) È В Í Х Í С Ç ( `А È В). Преобразуя правое

выражение, получим: С\А È В Í Х Í С\А È В.

Следовательно,Х = А\С ÈВ.

2. Решить систему уравнений

где А, В, С — данные множества и В Í А, А ÇС= Æ.

Ответ: Х=С È(А\В).

3. Решить систему уравнений

где А, В, С — данные множества и В Í А Í С.

Ответ: Х = С\В.

4. Решить систему уравнений

При каких А, В и С система имеет решение?

Два множества P и Q равны тогда и только тогда, когда пересечение

P Ç `Q =Æ и P È`Q=I.

1. Пусть А È Х = В Ç Х.

Тогда (А È Х) Ç (В ÇХ)= Æ. Преобразуем это выражение обычным образом:

(А È Х) Ç(`В È `Х)= (А Ç `В) È (А Ç `Х) È (`В Ç Х) = Æ.

Объединение множеств может быть пусто тогда и только тогда, когда пусты все множества, участвующие в объединении (по определению объединения). Т.е.

А Ç `В = Æ, Х Ç`В = Æ, А Ç `Х = Æ.

Из А Ç `В = Æ , следует, что А Í В.

Из Х Ç`В = Æ, следует, что то Х Í В.

Из А Ç `Х = Æ следует, что А Í Х.

Из полученных выражений получаем двойное включение А Í Х Í В и А Í В.

2. Пусть А Ç Х = С È Х.

Тогда (А ÇХ) Ç (С È Х) = Æ. Преобразуем это выражение обычным образом:

(А Ç Х) Ç (`С Ç `Х ) = Æ. Это тождественное равенство, так как Х Ç `Х = Æ по аксиоме дополнения. Поэтому перепишем преобразование иначе:

(А Ç Х) Ç (С È Х) = Æ. Отсюда

( `А È `Х ) Ç (С È Х) = ( `А Ç С ) È (`А Ç Х) È (С Ç `Х ) = Æ.

Из ( `А Ç С ) = Æ следует, что С Í А.

Из ( `А Ç Х) = Æ следует, что Х Í А.

Из (С Ç `Х) = Æ следует, что С Í Х .

Из полученных выражений получаем двойное включение С Í Х Í А и С Í А.

3. Объединяя полученные двойные включения, получим:

А È С Í Х Í А Ç В. Так как С Í А Í В, то А È С = А и А Ç В = А.

Окончательно получаем А Í Х Í А,т.е. Х=А.

4. Решить систему уравнений

При каких А, В, С система имеет решение?

Решение: Используем для решения тот же подход что и в задаче 3.

1. Пусть (А Ç Х) Ç (В Ç `Х ) = Æ. Отсюда получим: В Ç `А Í Х и В Í Х.

2. Пусть (С È Х) Ç (Х\А)= Æ. Отсюда — С Í Х Í `А.

3. Объединяя полученные в пунктах 1 и 2 включения, получим

В È С Í Х Í `Апри условии, чтоВ È С Í `А.

5. Решить систему уравнений и определить, при каких А, В, С система имеет решение.

Решение: Воспользуемся приемом задачи 3 настоящего раздела.

1. (А Ç `Х) Ç Х\В = Æ . Отсюда получим А Ç В Í Х и AÍX.

2. Х\А Ç С\Х = Æ. Отсюда — Х Í А È С и XÍA.

Объединяя полученные включения, получим

А Í Х Í А. Отсюда Х = А.

Не нашли то, что искали? Google вам в помощь!