Решение задач с помощью уравнений
Тема урока: § 6. Решение задач с помощью уравнений. Приведены все необходимые и достаточные сведения для решения текстовых задач с помощью составления уравнений.
Введение
В школьной математике есть целый кладезь текстовых задач, которые решаются универсальным методом построения уравнения (модели) исходя из условия.
Сам факт того, что огромное количество самых разнообразных задач поддаются решению с помощью составления линейного уравнения, говорит нам, что метод решений является действительно универсальным.
Обычно условия задач удается перевести на математический язык. Полученное уравнение — это следствие перевода нашего условия с русского языка на язык алгебры. Зачастую фактической стороной повествования задачи является описание реальной ситуации, какого либо процесса, события.
Чтобы получить ответ — уравнение нужно решить, полученный корень уравнения будет являться решением, разумеется необходимо еще проверить, не является ли результат противоречивым относительно условия.
Алгоритм решения текстовых задач с помощью уравнений
Для решения задачи с помощью уравнения делают следующие действия:
- Обозначают некоторое неизвестное буквой и, пользуясь условием, составляют уравнение.
- Решают уравнение.
- Истолковывают результат.
Примеры решений
Задача 1.
В мешке было в 3 раза меньше монет, чем в сундуке. После того как из мешка переложили 24 монеты, в сундуке их стало в 7 раз больше, чем в мешке. Сколько было монет в мешке и сколько в сундуке?
Пусть $x$ — количество монет в мешке, а значит в сундуке: $3x$ монет. После того, как из мешка переложили $24$ монеты, в сундуке стало: $3x+24$, а в мешке $x-24$. И если в сундуке их стало в $7$ раз больше чем в мешке, то имеем: $3x+24=7(x-24)$.
Ну вот мы и составили уравнение (математическую модель), осталось решить уравнение относительно $x$ и записать ответ.
Решим полученное уравнение: $3x+24=7(x-24)$. Легко увидеть, что уравнение является линейным (узнать как решаются линейные уравнения можно тут.)
Раскроем скобки в правой части уравнения: $3x+24=7x-7\cdot 24$. Перенесём все слагаемые содержащие переменную в правую часть, а всё что не содержит $x$ в левую, получим: $24+7\cdot 24=7x-3x$. После упрощения получили $192=4x$, разделим обе части уравнения на коэффициент при неизвестном, т.е на $4$, тогда получим $x=48$.
Осталось истолковать ответ.
За переменную $x$ мы обозначали количество монет в мешке, значит в сундуке в три раза больше т.е $3x$.
Монет в мешке: $48$
Монет в сундуке: $48\cdot 3=144$
Задача 2.
Купили 3600 кг муки и высыпали её в три мешка. В первый мешок муки вошло в 3 раза больше, чем во второй, а в третий мешок насыпали 800 кг муки. Сколько муки насыпали в первый и сколько во второй мешок?
Пусть в первый мешок насыпали $3x$ кг муки, тогда во второй мешок насыпали $x$ кг. Если сложим количество кг в каждом мешке, то получим $3600$ кг муки. Имеем: $3x+x+800=3600$, решим уравнение классическим методом.
Все слагаемые содержащие $x$ оставим слева, а всё остальное перенесём в правую часть равенства: $3x+x=3600-800$, упростим обе части; $4x=2800$ поделим обе части равенства на $4$ и получим ответ: $x=700$.
Ответ.
За переменную $x$ мы обозначали количество муки во втором мешке, по условию в первом в три раза больше.
Муки в первом мешке: $700\cdot 3=2100$ кг.
Муки во втором мешке: $700$ кг.
Задача 3.
В первом мешке в 4 раза больше картофеля, чем во втором. После того, как из одного мешка взяли 40 кг картофеля, а во второй насыпали ещё 5 кг, в обоих мешках картофеля стало поровну. Сколько килограммов картофеля было во втором мешке.
Пусть во втором мешке $x$ кг картофеля, тогда в первом мешке $4x$ кг. Из первого взяли $40$ кг, тогда в первом стало: $4x-40$. Во второй мешок насыпали $5$ кг и теперь в нём: $x+5$ кг картошки. Нам известно, что после этих изменений количество картофеля в мешках стало поровну, запишем это с помощью линейного уравнения:
Решим это линейное уравнение. Все слагаемые содержащие переменную перенесём влево, а свободные члены вправо и получим:
Избавимся от коэффициента при неизвестном и получим ответ:
Ответ.
За переменную $x$ мы обозначали количество кг картошки во втором мешке, по условию в первом в четыре раза больше.
Картошки в первом мешке: $15\cdot 4=60$ кг.
Картошки во втором мешке: $15$ кг.
Задача 4.
По шоссе едут две машины с одной и той же скоростью. Если первая увеличит скорость на 20 км/ч, а вторая уменьшит скорость на 20 км/ч, то первая за 2 часа пройдёт то же самое расстояние, что и вторая за 4 часа. Найдите первоначальную скорость машин.
Пусть машины едут со скоростью $v$ км/ч, тогда после ускорения первой машины её скорость стала: $v+20$ км/ч, а скорость второй машины после замедления стала: $v-20$ км/ч. Нам известно по условию, что после изменения скоростей машин, первая проходит за два часа ровно столько, сколько вторая за четыре, тогда имеем:
По известной нам формуле $S=vt$ ($S$ — расстояние, $v$ — скорость, $t$ — время)
Сократим обе части равенства на $2$, тогда получим: $v+20=2(v-20)$. Раскроем скобки в правой части уравнения и сгруппируем все переменные в правой части равенства.
Ответ.
В качестве неизвестной величины в задаче мы взяли $v$ (первоначальную скорость машин).
Первоначальная скорость машин: $v=60$ км/ч.
Задача 5.
В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую. Каждый час работы первая бригада расходовала 150 кг раствора, а вторая – 200кг. Через 3 ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Сколько раствора привезли в каждую бригаду?
Пусть во вторую бригаду привезли $x$ кг раствора цемента, тогда в первую бригаду привезли $x-50$ кг. Через 3 часа работы у первой бригады осталось $x-50-3\cdot 150$ кг цемента, а у второй $x-3\cdot 200$ кг.
По условию известно, что через 3 часа работы в первой бригаде осталось в 1,5 раза больше цемента, чем во второй, тогда имеем:
$$x-50-3\cdot 150=1,5(x-3\cdot 200)$$
Осталось решить данное уравнение относительно $x$ и истолковать ответ.
Упростим и раскроем скобки в правой части, тогда получим:
Если вам неудобно работать с десятичными дробями, то вы всегда можете их переводить в рациональный вид: $1,5=\frac<15><10>=\frac<3><2>$.
Запишем с учётом перевода дробей и упростим:
Перенесём слагаемые содержащие переменную в правую сторону, а всё остальное в левую:
Домножим обе части на 2 и получим ответ:
Ответ.
В качестве переменной в задаче мы взяли $x$ (кол-во кг цемента который привезли во вторую бригаду), по условию в первую привезли на 50 кг меньше, а значит $x-50$
Кол-во цемента в первой бригаде: $800-50=750$ кг.
Кол-во цемента во второй бригаде: $800$ кг.
Задачи для самостоятельного решения
По контракту работникам причитается 48 франков за каждый отработанный день, а за каждый неотработанный день с них вычитается по 12 франков. Через 30 дней выяснилось, что работникам ничего не причитается. Сколько дней они отработали в течение этих 30 дней?
Пусть работники отработали $n$ дней, тогда $30-n$ дней они не отработали.
В итоге мы понимаем, что за $n$ рабочих дней они зарабатывают $48n$ франков и с них вычитается за $30-n$ не отработанных дней по $12(30-n)$ франков. Тогда ясно, что: $48n-12(30-n)=0$
Ответ: Рабочие отработали 6 дней.
Кирпич весит фунт и полкирпича. Сколько фунтов весит кирпич?
Пусть целый кирпич весит весит $k$ фунтов, тогда имеем:
1 фунт и половина кирпича = целый кирпич.
Бутылка с пробкой стоит 10 копеек, причем бутылка на 9 копеек дороже пробки. Сколько стоит бутылка без пробки?
Пусть бутылка стоит $b$ копеек, а пробка $p$ копеек, тогда:
$b+p=10$ и $b=p+9$, подставив значение $b$ в первое равенство — получим:
Т.е пробка стоит пол копейки, тогда бутылка $9,5$ копеек.
Ответ: 9,5 копеек стоит бутыка без пробки.
На свитер, шапку и шарф израсходовали 555 г шерсти, причем на шапку ушло в 5 раз меньше шерсти, чем на свитер, и на 5 г больше, чем на шарф. Сколько шерсти израсходовали на каждое изделие?
Пусть на свитер потратили $5x$ г шерсти, тогда на шапку ушло $x$ г и на шарф потребовалось $x-5$ г, имеем:
Ответ: На шапку ушло $80$ г, на свитер $5\cdot 80=400$ г, на шарф $80-5=75$ г.
Три пионерских звена собрали для школьной библиотеки 65 книг. Первое звено собрало на 10 книг меньше, чем второе, а третье — 30% того числа книг, которое собрали первое и второе звено вместе. Сколько книг собрало каждое звено?
Пусть второе звено собрало $x$ книг, тогда первое собрало $x-10$ книг, а третье $0,3(2x-10)$, имеем:
$$2x-10+0,3\cdot 2x-0,3\cdot 10=65$$
$$2x+0,3\cdot 2x=65+10+0,3\cdot 10$$
Ответ: Первое звено собрало $30-10=20$ книг, второе $30$ книг, третье $0,3(60-10)=15$ книг.
Решение задач методом составления уравнений. Методические рекомендации.
Наука и жизнь требует от школы не только сообщения определенных познавательных фактов своим воспитанникам, но и систематического ознакомления их с идеями и методами науки, передачи им интеллектуального опыта человечества. Очень важно научить обучаемых необходимым приемам рассуждений.
Просмотр содержимого документа
«Решение задач методом составления уравнений. Методические рекомендации.»
Решение задач методом составления уравнений
В методической литературе, в практике лучших учителей большое внимание уделяется воспитательной задаче обучения математике, формированию и развитию мышления обучающихся, выработке рациональных качеств мышления (порядка точности, краткости, схематичности).
Особое значение при этом приобретает выработка общих и специальных методов решения задач, формирование умений и навыков математической обработки различных фактов реальной жизни.
Наука и жизнь требует от школы не только сообщения определенных познавательных фактов своим воспитанникам, но и систематического ознакомления их с идеями и методами науки, передачи им интеллектуального опыта человечества. Очень важно научить обучаемых необходимым приемам рассуждений.
Важно не только сообщить учащимся сведения об этих приемах и методах, но и добиться того, чтобы приобретенные знания о методах обучающиеся знали и умело применяли. В современных учебниках и сборниках для учащихся недостаточно указаний, касающихся обще логических и специальных методов познания, применяемых в школе.
1.Идеи и принципы содержания и методики решения задач.
Обучение учащихся решению задач содержит в себе две важные составные части: выполнение подготовительных упражнений и решение текстовых задач.
В процессе обучения решению задач обучающиеся должны в известной мере овладевать основными идеями школьной математики, а именно:
соответствия, порядка, расположения;
доказуемости заключений относительно свойств пространственных форм и количественных соотношений в них;
применимости числа и меры к явлениям окружающегося мира.
Система работ по формированию у школьников умений и навыков выполнение подготовительных упражнений и решения задач должна строиться:
1.Гносеологический принцип познания- единство анализа и синтеза.
2. Методико-математические принципы: идейно-теоретическая направленность в обучении, особенно использование идей функциональной зависимости.
Овладение логическими и специальными методами познания, применяемыми при изучении математики в школе, особенно методами исследования различных процессов на основе учета всех возможных разновидностей данной ситуации, всех возможных соотношений между величинами, входящих в задачу.
Конструктивный подход к решению задач. Перспективный подход к решению задач, принцип обратной связи.
Повторяемость упражнений по спирали с постепенным усложнением, включением новых знаний в систему ранее приобретенных.
Самостоятельность выполнения упражнений, каждым учеником, внедрение элементов индивидуализации обучения детей в коллективе.
Самообучение и взаимное обучение в сотрудничестве.
Задачи школьной математики сводятся к небольшому числу зависимостей, которые приводят к нескольким типам уравнений.
Некоторые авторы указывают следующие виды уравнений, к которым сводится решение задач методом составления уравнений первой степени.
1-й тип задач. Задачи, приводящие к уравнениям вида f(x)= c.Например, ах+в=с.
Задачи этого типа тесно связаны с арифметическими задачами на зависимость между компонентами и результатами действий. Сюда относятся и задачи на деление с остатком.
2-й тип задач. Задачи, приводящие к уравнению вида: f(x)=g(x). Например, ах+в=сх+d.
Эти задачи алгебраического характера.
3-й тип задач. Задачи, приводящие к разностному и краткому сравнению величин путем сопоставления значений двух алгебраических выражений однородных величин. Решение таких задач приводит к уравнениям вида:
В некоторых пособиях третий тип рассматривают как варианты второго типа.
Задачи школьной математики, приводящие к квадратным уравнениям, в своей основе содержат комбинации двух линейных функций и их произведений, а также соотношения между функциями второй степени, аналогичные соотношениям, приведенным в трех типах задач для уравнений первой степени.
Функциональный подход к решению задач будет содействовать формированию у обучающихся умений и навыков в исследовании процессов реальной жизни, развитию их функционального мышления, способностей в анализе и синтезе, в индукции и дедукции. Без функционального подхода мы волей-неволей будем учить лишь решению отдельных задач, в итоге учащиеся из-за этих задач не увидят математики, ее идей и методов. Особое значение в развитии функционального мышления имеет составление таблиц, схем, графиков, диаграмм и формул.
2.Организация процесса обучения школьников при решении задач.
Рассматривая содержание и методику подготовительных упражнений, мы должны ответить на вопросы:
Какие упражнения следует выполнять?
Зачем их выполнять?
Когда их выполнять?
Как при этом будут работать дети, какие качества при этом у них будут воспитываться?
Что и зачем выполнять? Подготовительные упражнения можно разбить на две группы:
Система упражнений, не связанных с изучением текущего материала. Цель таких упражнений- систематическое повторение основных фактов и теоретических положений, уяснение логики и структуры изучаемой дисциплины.
Система упражнений, преследующих подготовку обучаемых к решению составных задач, с которыми обучающиеся ранее не встречались.
Эти два положения отвечают на первые два вопроса, что выполнять и зачем выполнять.
Важное значение для составления уравнения по условию задач имеют навыки и записи алгебраических выражений, равенств, неравенств с целью уяснений основных понятий и соотношений: равно, больше на столько-то, больше во столько-то, процент, отношение.
Для отработки этих понятий и соотношений между ними необходимы систематические упражнения в записи алгебраических выражений во всех классах основного общего образования. Существенно важно, чтобы упражнения носили не только абстрактный характер, но и характер практически реальных задач.
Полезно, чтобы каждый ученик приобрел умения и навыки записи под диктовку учителя алгебраических выражений, соответствующих сущности основных понятий, зависимостей и соотношений. Большое значение имеет запись формул, выражающих функциональную зависимость между величинами. Упражнения такого рода важны для уяснения учащимися сущности функциональной зависимости, аналитического выражения этой зависимости, развития функционального мышления.
Приведем упражнения, которые целесообразно давать систематически, повторяя их время от времени.
Скорость равномерного движения тела v, время движения t, путь s. Запишите формулы для определения s, v, t.
Цена товара К, количество m, стоимость c. Запишите формулы зависимости между c, m, К.
Производительность труда n, время работы t, объём выполненной работы А. Выразите зависимость между формулами для А, n и t.
Приняв объём работы за 1, запишите формулу зависимости между производительностью n, временем необходимым для выполнения этой работы, t и объёмом работы 1.
Мощность двигателя w, время работы t, работа А. Выразите зависимость формулами для А, w и t.
Расход горючего на 1км пути составляет n л/км, пробег машины s км, объём израсходованного горючего v л. Выразите зависимость формулами для v, s и n.
Резервуар объёмом V наполняется трубой за t ч, производительность трубы n л в час. Выразите зависимость между величинами V, n и t.
Вкладчик внес в кассу, а руб. по 3% годовых. Выразите его капитал через год формулой, обозначив этот капитал буквой А.
Вкладчик внес в банк, а руб. по р% годовых. Выразите его капитал через год обозначив этот капитал буквой К.
10.Выразите зависимость между массой m, объёмом V и плотностью d. Запишите выражения для каждой величины.
При делении 20 на 6 в частном получается 3 и в остатке 2. Свяжите все эти числа формулой. Выразите каждое число через другие.
Выразите формулой зависимость между делимым, а, делителем в, частным g и остатком r.Выразите каждое число через остальные.
Составьте эскизы известных фигур и запишите формулы для вычисления их площадей, обозначив стороны основания буквами, а и в, высоту буквой h, радиус r, площадь S с соответствующими индексами, например, площадь треугольника S3.
Запишите формулы для вычисления объёмов известных тел, составив предварительно эскизы и обозначив необходимые элементы.
Урожай с одного гектара a ц/га, площадь S га, вес урожая Р ц. Выразить зависимость между, а, S и Р формулой.
В отдельных упражнениях целесообразно указывать наименование величин.
Подготовительные упражнения полезно выполнять во всех разделах школьной математики в сочетании с изучением текущего материала.
Перед решением сложных задач полезны постепенно усложняющиеся упражнения, приводящие в конечном итоге рассматриваемому типу задач. Главным в этих упражнениях следует считать выявление закономерностей, установление функциональной зависимости, выражение этой зависимости формулой.
Рассмотрим несколько задач, при решении которых выявление закономерностей приводит к необходимому уравнению.
Задача. При выпечке ржаного хлеба припек составляет 0,3 массы взятой муки. Сколько муки нужно взять, чтобы получить 26 кг печеного хлеба?
В задаче очень важно установить функциональную зависимость между весом муки, весом печеного хлеба и припеком.
В этих целях полезно составить следующую таблицу, отражающую своеобразный эксперимент по составлению задач.
Во втором и последующих случаях результаты записываются на основании пропорциональности веса хлеба и муки.
В итоге проведенного исследования получается общая формула для решения прямой и обратной связи. Рх=1,3*Рм , Рм=Рх/1,3
Она же дает возможность определить коэффициент пропорциональности и процент припека К из формулы Рх=К* Рх
Сам процесс решения таких задач способствует тому, чтобы учащиеся овладевали идеей функциональной зависимости между величинами, входящими в задачу, методами и техникой расчетов.
Можно высказать одно общее пожелание учителям: прежде чем приступить с учениками к решению составной задачи, целесообразно на уроке составить вместе с ними аналогичную задачу из основных простых, комбинируя и усложняя последние. Тот, кто научился хорошо строить, будет хорошо разбирать построенное без лишних потеть времени и сил.
Когда выполнять подготовительные упражнения?
Упражнения, не связанные с изучением текущего материала, направленные на усвоение основных фактов, идей и методов, целесообразно выполнять систематически с определенной повторяемостью, по спирали. Обогащая известное новыми фактами. Из опыта работы учителей установилось правило каждый вид основных упражнений повторять ежемесячно. Не следует стремится к тому, чтобы подобные упражнения выполнялись на каждом уроке, но и нецелесообразно делать чрезмерно длительные перерывы в их выполнении. В зависимости от содержания урока упражнениям отводится различное время. Если урок посвящен изучению нового материала, то повторительные упражнения можно отнести на конец урока. На уроках закрепления материала такие упражнения целесообразно давать в начале урока. В некоторых случаях подобные упражнения можно включать небольшими порциями в изложение материала урока.
Как выполнять упражнения? Как при этом будут работать дети?
Существуют различные способы и приёмы активизации выполнения упражнений каждым учеником.
Если учитель диктует условие и предлагает ученикам кратко в символической форме записать его, то при этом почти не бывает неработающих детей. Для учащихся фиксирование условия является своеобразным включением в работу. В этот период каждый из них мобилизует свои чувства и мышление на дальнейшую активную работу.
Например, учитель диктует: Найти число ,2/3 которого равны 12,6. После слов учителя «Найти число» дети пишут в своих тетрадях: х; после слов «2/3 которого» они пишут: х* 2/3; наконец, записывают: х*2/3=12,6
Таким образом, некоторая часть работы уже выполнена самостоятельно, остаётся ее продолжить. Хорошо известная истина- трудно начало дела. Когда начало положено, то дальнейшая работа уже совершается с определенным интересом. Поэтому после записи условия пример решают все обучающиеся.
Вместо диктанта полезно во многих случаях записывать условие задачи на доске в словесной форме. Учащиеся записывают его в символах в своих тетрадях и затем выполняют действия.
Во многих случаях условие может быть изображено учащимися с помощью чертежей и других иллюстраций. Например, пусть решается задача: Определить сторону квадрата, если с увеличением одной из его сторон на 2 см, а другой на 3 см. Площадь полученного прямоугольника будет на 21 см 2 больше, чем площадь квадрата. После слов «определить сторону квадрата» рисуют квадрат и пишут на его сторонах: х. После слов «с увеличением одной стороны на 2см, а другой на 3см» учащиеся чертят прямоугольник, на сторонах которого пишут «х+2 и х+3». Затем внутри фигур пишется формула для вычисления площади, и затем задача решается. Такой порядок решения задачи дает возможность учащимся ощутить и образно представить величины, входящие в задачу, и зависимость между этими величинами. После записи условия в краткой форме учащиеся выполняют задание устно, а в необходимых случаях письменно.
Таким образом, можно наметить следующую схему выполнения упражнений: Сообщение текста учителем, символическая запись учащимися условий, устное или полу письменное решение, запись ответа, проверка решения учителем, или взаимная проверка решения учащимися, или самостоятельная проверка решения.
При любом способе выполнения упражнения оно должно быть проверено самим учеником по контрольным ответам, записанным на доске, или учителем. Если упражнения даются с целью повторения и воспроизведения знаний, то полезно организовать взаимную проверку; если же учитель хочет выставить оценки за упражнения, то проверять должен сам.
Логико-психологические этапы решения задачи.
Правило решения задач.
Надежность деятельности ученика к решению задач обуславливается его умением выбора нужных операций, приводимых к получению нужного результата. Выбор операций, определяется структурой задачи, а также сформированностью приёмов умственной учебной деятельности обучающихся. Из этого вытекает необходимость расчленения задачи на составные элементы, отбор и составление этих элементов в ином плане, обеспечивающем активную работу учащимся. Из этого также вытекает необходимость разделения хода решения задачи на отдельные логико- психологические этапы, каждый из которых представляет собой определенную законченную часть решения задачи, дающую возможность осуществить операции следующего этапа.
В логико- психологическом плане такие этапы, содержащие определенные рекомендации, представляют собой программу деятельности учащихся, вызывающую соответствующие операции на уровне познавательных компетенции восприятия и мышления.
Без конкретной программы деятельности учащихся, без алгоритмов или общих указаний по поиску решения задач, по всей видимости, трудно организовать процесс обучения детей, ибо этот процесс имеет своими частями подражание и творчество.
В каждой задаче имеются явные и неявные данные и зависимости между величинами. Явные данные и зависимости психологически представляют собой сильные раздражители. Неявные данные, и особенно неявно выраженные зависимости, являются слабыми раздражителями, и поэтому дети в процессе решения задач часто не учитывают их, пропускают и как итог не справляются с решением задач.
Одна из важных задач учителя как раз и заключается в том, чтобы научить детей делать неявное явным, слабые раздражители сильными, научить детей выявлять и учитывать все данные и зависимости условия задачи.
Процессы реальной жизни характеризуются величинами, между которыми существуют определенные зависимости. Поэтому целесообразно научить детей начинать решение всякой задачи с установления процессов, описываемых в задаче, затем выявлять величины, характеризующие каждый процесс, уяснить функциональную зависимость между величинами. Все это представляет анализ задачи на функциональной основе, своеобразную теорию задачи.
Установление процессов, выявление величин и уяснение функциональной зависимости между величинами, входящими в задачу, поможет учащимся неявно выраженные данные и зависимости сделать явно выраженными, подготовить базу для решения задачи.
Выделим следующую схему и основанные на ней рекомендации.
этап. Анализ и собственная запись условия задачи. Анализ чертежа, если он необходим и построен. Сюда относятся: а) установление объекта наблюдения (исследования);
б) выделение процессов, подлежащих рассмотрению;
в) выявление величин, входящих в каждый процесс;
г) уяснение функциональной зависимости между величинами и составление формул этой зависимости;
д) схематическая запись условия задачи с обозначением неизвестных величин.
этап. Выявление оснований для составления уравнения или системы уравнений.
этап. Составление уравнения или системы уравнений.
этап. Решение уравнения или системы уравнений.
этап. Исследование корней уравнения (системы) с целью установлений решений задачи. Смысловой анализ решения задачи. Проверка расчетов и обоснований.
Анализ решения задачи. Рефлексия. Рассмотрение всех вариантов решения задачи. Выяснение возможности обобщения. Установление общих правил для решения подобных задач. Поиск более рациональных приемов решения задач.
Рассмотрим подробно каждый этап и рекомендации для учащихся при решении следующей задачи:
Автобус проходит расстояние АВ, равное 120 км, равномерно за определенное время. Через час после отправления из А, автобус был задержан у шлагбаума на 10 минут и, чтобы прибыть в пункт В по расписанию, должен был увеличить скорость на 6 км/ч. Найти первоначальную скорость.
Этап. Анализ и собственная запись условия задачи.
Математическое описание процесса заключается в установлении величин, характеризующих этот процесс, в выявлении закономерных связей между величинами, в записи формул, уравнений, или вычерчивании графиков, отражающих эти зависимости, в определении неизвестных различными способами.
Следующим шагом должно быть осознание структуры задачи, выявление неявных данных и зависимостей между величинами. Целесообразно, чтобы задача при этом была расчленена на составные части и записана каждым из учеников по-своему, но так, чтобы ничего не было упущено из ее условия.
Важно, чтобы при решении задачи явные и неявные ее данные были приведены во взаимодействие, чтобы ученики провести эксперимент с целью получения частных соотношений, на основе которых устанавливаются общие зависимости, закономерности, а затем различными способами выразить один и тот же факт.
По первому этапу целесообразно, чтобы ученикам были даны следующие рекомендации:
1) Уясните смысл текста задачи и значение каждого слова. Вспомните или прочитайте определение понятий, входящих в условие задачи.
2) Установите объект исследования (наблюдения).
3) Выявите процессы, описываемые в задаче. Заметьте сколько их, сколько раз придется вести наблюдение, сколько раз придется вести записи.
4) Укажите величины, характеризующие каждый процесс, обозначьте их и проставьте единицы измерения, уясните зависимость между величинами и запишите ее формулой. Если трудно написать формулу сразу в общем виде, запишите ее на частных примерах, а затем в общем виде.
5) Запишите условие задачи в понятной и доступной вам форме, для чего: выберите одну из неизвестных величин и обозначьте ее буквой, составьте для каждого процесса задачи алгебраические выражения. включая данные н неизвестные. Не забудьте о выбранных единицах измерения. Упростите выражения.
6) Расположите записанные алгебраические выражения в порядке, удобном для расчетов и сравнений, используйте при этом таблицу, график, рисунок или текстовое пояснение.
При решении приведенной выше задачи целесообразно составить графическую иллюстрацию условия задачи, на которую по мере анализа задачи следует нанести данные и неизвестные.
В тетрадях пишут:
s1=x км t2 = 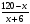
Иллюстрация и дополнительные подрисовки (стрелки, знаки, символы и т.д.) содействуют более отчетливому представлению отношений между частями задачи, связей и нередко приводят непосредственно к желаемому результату.
Величины, характеризующие каждый вид движения (процесс): скорость v км/ч, время t ч, путь s =v t (учащимся со слабой успеваемостью целесообразно предложить записывать и производные формулы v=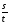
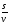
Решение задач составлением уравнения
Разделы: Математика
«Умственную самодеятельность, сообразительность и смекалку нельзя ни «вдолбить», ни «вложить» ни в чью голову. Результаты надёжны лишь тогда, когда введение в область математических знаний осуществляется в лёгкой и приятной форме, на предметах и примерах обыденной и повседневной обстановки, подобранных с надлежащим остроумием и занимательностью».
Е.И. Игнатьев «В царстве смекалки»
Цель обучающая: Научить анализировать условие задачи, выбирать рациональные способы решения, составлять уравнение, решать его, проверять правильность решения.
Цель воспитательная: Развитие абстрактного и логического мышления.
I. Актуализация опорных знаний.
1) Что называется уравнением? Что называется корнем уравнения? Что значит решить уравнение?
2) Решите уравнение 
Решение: а) 


б) НОЗ=6; 



3) Составьте буквенное выражение.
Наташа купила блокнот за m рублей, книгу на 20 рублей дороже блокнота и ручку в 2.5 раза дешевле книги. Сколько рублей стоит ручка?
Решение: (m+20) рублей цена книги, 
4) Из двух сёл, расстояние между которыми 10 км навстречу друг другу вышли мальчик и девочка и встретились через 2 часа. Скорость мальчика 3 км/час. Найдите скорость девочки.
Решение: а) 3*2=6(км) прошел мальчик, 10-6=4(км) прошла девочка, 4:2=2(км/ч) скорость девочки
б) 10:2=5(км/ч) скорость сближения, 5-3=2(км/ч) скорость девочки.
II. Сообщение темы и цели урока.
III. Решение задач составлением уравнения.
1) Андрей старше Олега на 4 года, а Олег старше Бориса в 1,5 раза. Вместе им 36 лет. Сколько лет каждому из них?
Первый ряд решает задачу, взяв за неизвестную величину возраст Андрея, второй ряд — возраст Олега, третий ряд-возраст Бориса. А затем каждый ряд объясняет своё решение у доски.
| Условие задачи | Решение уравнения | Проверка |
| Х лет Андрею, |  | 16+12+8=36 |
| Х лет Олегу |  | 12+16+8=36 |
| Х лет Борису (1,5х+4) лет Андрею |  | 8+12+16=36 |
Если в задаче несколько неизвестных величин, лучше обозначить буквой наименьшую из них.
2) Два пешехода вышли одновременно навстречу друг другу из двух посёлков и встретились через 3ч. Расстояние между посёлками 30 км. Найдите скорость каждого пешехода, если у одного она на 2 км/ч меньше, чем у другого.
а) Ученики решают задачу составлением уравнения.
Х км/ч – скорость 1-го пешехода
(х+2) км/ч – скорость 2-го пешехода
3х км прошел 1-й пешеход
3(х+2) км прошел 2-й пешеход
| 3х+3(х+2)=30 | 4 |
| 3х+3х+6=30 | +6 |
| 6х+6=30 | +12 |
| 6х=24 | +18 |
| Х=4 | =30 |
б) Затем решают арифметическим способом.
10-2=8(км/ч)-две скорости 1-го пешехода.
8:2=4(км/ч)-скорость 1-го пешехода.
4+2=6(км/ч)-скорость 2-го пешехода.
Вывод. Арифметическое решение задачи более рациональное
3)Для распечатки 340 страниц были использованы две копировальные машины. Первая машина работала 10 минут, а вторая 15 минут. Сколько страниц в минуту печатает каждая машина, если первая печатает на 4 страницы больше, чем вторая?
Снова дети решают задачу алгебраически и арифметически.
А) х страниц за 1 минуту печатает 2-я машина,
(х+4) страниц за 1 минуту напечатает 1-я машина,
15х страниц напечатает 2 машина,
10(х+4) страниц напечатает 2 машина,
| 15х+10(х+4=340 | 12 |
| 15х+10х+40=340 | +16 |
| 25х+40=340 | +180 |
| 25х=300 | +160 |
| Х=12 | =340 |
б) 10*4=40(стр) на столько страниц больше напечатает 1-я машина за 10 минут
340-40=300(стр) напечатали бы обе машины вместе, если бы у них были одинаковые скорости.
10+15=25(мин) работали обе машины.
300:25=12(стр) за 1-у минуту печатает 2-я машина.
12+4=16 (стр) за 1-у минуту печатает 1-я машина.
При решении задач с помощью уравнения поступают следующим образом:
- Внимательно читают условие задачи.
- Обозначают неизвестную величину буквой.
- Переводят условие задачи на алгебраический язык.
- Составляют уравнение.
- Решают уравнение.
- Проверяют правильность решения
V. Домашнее задание.
Решить задачу алгебраически и арифметически.
Охотничья собака спугнула зайца, который сидел под кустом в 150м от неё. Через сколько минут собака догонит зайца, если она пробегает за 6 минут 3,6км, а заяц только 3км?
- Л.В. Кузнецова, Е.А. Бунимович, Б.П. Пигарев, С.Б. Суворова «Алгебра» сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. Москва. «Дрофа». 2001г; стр 43, работа №31, вариант 1(5); стр 50, работа №38, вариант 2(7); стр 65, работа №48, вариант 1(6).
- Составители Т.А. Братусь, Н.А. Жарковская, Е.А Рисс, Т.Е Савелова «Детский математический календарь 2001-2002». Санкт — Питербург стр10.
- Н.Т. Кострикина «Задачи повышенной трудности в курсе алгебры 7-9 классов». Москва. «Просвещение» 1991 стр5-19.
http://multiurok.ru/files/rieshieniie-zadach-mietodom-sostavlieniia-uravnien.html
http://urok.1sept.ru/articles/505458



 лет Борису,
лет Борису,

 лет Борису
лет Борису