Амплитуда силы тока в уравнении

Переменный электрический ток

теория по физике 🧲 колебания и волны

Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.

Переменный ток — вынужденные электромагнитные колебания.

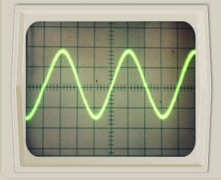
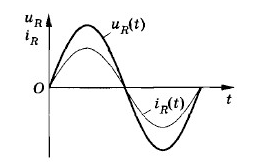
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:

Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.

Частота переменного тока — это количество колебаний за 1 с.

Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.

Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.

При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙10 8 м/с).

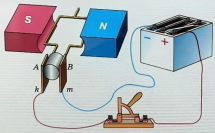
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).

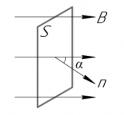
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.

Численно магнитный поток определяется формулой:

При равномерном вращении рамки угол α увеличивается пропорционально времени:

где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:

Φ = B S cos . 2 π n t

Здесь множитель 2 π n представляет собой число колебаний магнитного потока за 2 π секунд. Это не что иное, как циклическая частота колебаний:

Φ = B S cos . ω t

Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:

e = − Φ ´ = − B S ( cos . ω t ) ´ = B S ω sin . ω t = ε m a x sin . ω t

ε m a x — амплитуда ЭДС индукции, равная:

Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:

u = U m a x sin . ω t

u = U m a x cos . ω t

где U m a x — амплитуда напряжения (максимальное по модулю значение напряжения).

Сила тока меняется с той частотой, что и напряжение — ω . Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:

i = I m a x sin . ( ω t + φ с )

где I m a x — амплитуда силы тока (максимальное по модулю значение силы тока), φ с — разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.

u = U m a x cos . ω t = 12 cos . 300 , 25 π = 12 √ 2 2 . . ≈ 8 , 5 ( В ) .

Активное сопротивление в цепи переменного тока

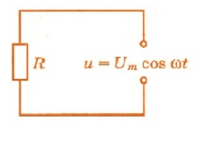
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).

Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.

Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:

u = U m a x cos . ω t

Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:

i = u R . . = U m a x cos . ω t R . . = I m a x cos . ω t

В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:

I m a x = U m a x R . .

Мощность в цепи с резистором

В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.

Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.

Мощность постоянного тока определяется формулой:

Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:

Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:

p = ( I m a x cos . ω t ) 2 R

Вспомним из курса математики:

cos 2 . α = 1 + cos . 2 α 2 . .

p = I 2 m a x 2 . . R ( 1 + cos . 2 ω t ) = I 2 m a x R 2 . . + I 2 m a x R 2 . . cos . 2 ω t

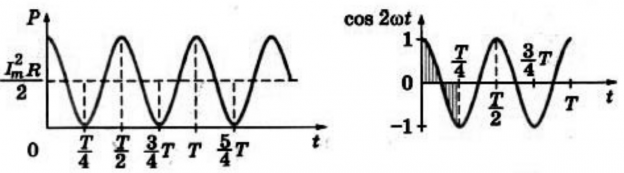
График зависимости мгновенной мощности от времени:

На протяжении первой четверти периода, когда cos . 2 ω t > 0 , мощность в любой момент времени больше величины I 2 m a x R 2 . . . На протяжении второй четверти периода, когда cos . 2 ω t 0 , мощность в любой момент времени меньше этой величины. Среднее за период значение cos . 2 ω t = 0 , следовательно, средняя за период мощность равна I 2 m a x R 2 . . .

Средняя мощность − p равна:

− p = I 2 m a x R 2 . . = − i 2 R

Пример №2. Сила переменного тока в цепи меняется по закону i = I m a x cos . ω t . Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.

p = ( I m a x cos . ω t ) 2 R = 10 ( 1 · cos . ( 100 π · 1 ) 2 = 10 ( Д ж )

Действующие значения силы тока и напряжения

Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:

− i 2 = I 2 m a x 2 . .

Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.

I = √ − i 2 = I m a x √ 2

Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.

Аналогично определяется действующее значение напряжения U:

U = √ − u 2 = U m a x √ 2 . .

Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:

Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.

P = ( I m a x √ 2 . . ) 2 R = I 2 m a x 2 . . R = 2 2 2 . . · 5 = 10 ⎛ ⎝ Д ж ⎞ ⎠

В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону U_C = U₀cos ωt, где U₀ = 5 В, ω = 1000π с – «> – 1 . Определите период колебаний напряжения на конденсаторе.

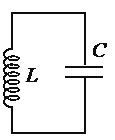
Период, частота, амплитуда и фаза переменного тока

Период и частота переменного тока

Время, в течение которого совершается одно полное изме­нение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания пере­менного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.

Период выражают в секундах и обозначают буквой Т.

Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.

1 мс =0,001сек =10 -3 сек.

1 мкс=0,001 мс = 0,000001сек =10 -6 сек.

Число полных изменений ЭДС или число оборотов ради­уса-вектора, то есть иначе говоря, число полных циклов колеба­ний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.

Частота обо­значается буквой f и выражается в периодах в секунду или в герцах.

Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.

1000 Гц = 10 3 Гц = 1 кГц;

1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Чем быстрее происходит изменение ЭДС, то есть чем бы­стрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.

Математическая связь между периодом и частотой переменного тока и напряжения выра­жается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

Т = 1/f = 1/50 = 0,02 сек.

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:

f = 1/T=1/0,02 = 100/2 = 50 Гц

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Частоты от 20 до 20 000 Гц называются звуковыми часто­тами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие вы­сокие частоты называются радиочастотами или колебаниями высокой частоты.

Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.

Амплитуда переменного тока

Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно бук­вами Im, Em и Um (рисунок 1).

Угловая (циклическая) частота переменного тока.

Скорость вращения радиуса-вектора, т. е. изменение ве­личины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (оме­га). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.

Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.

Рисунок 2. Радиан.

1рад = 360°/2

Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в тече­ние одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его ко­нец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .

? = 6,28*f = 2f

Фаза переменного тока.

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза пока­зывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.

Полный оборот радиуса-вектора равен 360°. С началом но­вого оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следова­тельно, все фазы ЭДС будут повторяться в прежнем поряд­ке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обо­их этих случаях радиус-вектор занимает одинаковое положе­ние, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Электромагнитные колебания

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Колебательный контур

Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.

Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.

Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.

Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.

Начальный момент: . Заряд конденсатора равен , ток через катушку отсутствует (рис. 1 ). Конденсатор сейчас начнёт разряжаться.

Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.

Аналогия. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.

Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2 ).

Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.

Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.

Конец первой четверти : . Конденсатор полностью разрядился. Сила тока достигла максимального значения (рис. 3 ). Сейчас начнётся перезарядка конденсатора.

Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.

Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения . Деформация пружины равна нулю.

Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4 ).

Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.

Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.

Конец второй четверти . Конденсатор полностью перезарядился, его заряд опять равен (но полярность другая). Сила тока равна нулю (рис. 5 ). Сейчас начнётся обратная перезарядка конденсатора.

Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна .

Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6 ).

Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.

Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен , но на сей раз имеет другое направление (рис. 7 ).

Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью , но на сей раз в обратном направлении.

Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8 ).

Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.

Конец четвёртой четверти и всего периода: . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9 ).

Данный момент идентичен моменту , а данный рисунок — рисунку 1 . Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.

Аналогия. Маятник вернулся в исходное положение.

Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!

Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.

В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.

Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.

Энергетические превращения в колебательном контуре

Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .

Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.

Возьмём момент времени, когда заряд конденсатора максимален и равен , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:

Теперь, наоборот, рассмотрим момент, когда ток максимален и равен , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:

В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:

Соотношение (1) применяется при решении многих задач.

Электромеханические аналогии

В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.

Для пружинного маятника мы имеем соотношение, аналогичное (1) :

Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.

Сопоставляя друг с другом равенства (1) и (2) , мы видим следующие соответствия:

Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.

В самом деле, период колебаний пружинного маятника, как мы знаем, равен:

B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость . Получим:

Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.

Гармонический закон колебаний в контуре

Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».

Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10 ).

Рис. 10. Положительное направление обхода

Сила тока считается положительной 0)’ alt='(I > 0)’ /> , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной .

Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.

При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если 0′ alt=’I > 0′ /> , то заряд левой пластины возрастает, и потому 0′ alt=’\dot > 0′ /> .

Величины и меняются со временем, но энергия контура остаётся неизменной:

Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8) ; не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ):

Подставляя сюда и , получим:

Но сила тока не является функцией, тождественно равной нулю; поэтому

Перепишем это в виде:

Мы получили дифференциальное уравнение гармонических колебаний вида , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:

Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:

Мы снова пришли к формуле Томсона.

Гармоническая зависимость заряда от времени в общем случае имеет вид:

Циклическая частота находится по формуле (10) ; амплитуда и начальная фаза определяются из начальных условий.

Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при заряд конденсатора максимален и равен (как на рис. 1 ); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой :

Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12) , опять-таки не забывая о правиле нахождения производной сложной функции:

Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:

Амплитуда силы тока равна:

Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2 ).

Ток течёт в отрицательном направлении: . Поскольку , фаза колебаний находится в первой четверти: . Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13) .

А теперь посмотрите на рис. 8 . Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!

Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13) . Для наглядности представим эти графики в одних координатных осях (рис. 11 ).

Рис. 11. Графики колебаний заряда и тока

Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.

Используя формулу приведения

запишем закон изменения тока (13) в виде:

Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная , больше фазы заряда на величину . В таком случае говорят, что ток опережает по фазе заряд на ; или сдвиг фаз между током и зарядом равен ; или разность фаз между током и зарядом равна .

Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево на относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз ).

Вынужденные электромагнитные колебания

Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.

Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12 ).

Рис. 12. Вынужденные колебания

Если напряжение источника меняется по закону:

то в контуре происходят колебания заряда и тока с циклической частотой (и с периодом, соответственно, ). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте .

Амплитуда вынужденных колебаний заряда и тока зависит от частоты : амплитуда тем больше,чем ближе к собственной частоте контура .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.