Решение линейных уравнений с параметром аналитическим и графическим способами (7-й класс)
Разделы: Математика
Класс: 7
Цель урока: научиться решать уравнения с параметром линейного вида.
- ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ.
Выполненные на отдельных листах упражнения из домашнего задания, вывешиваются перед уроком на специальной доске для самопроверки.
На конференции 85% делегатов знают английский язык и 75 % испанский. Какая часть делегатов знают оба языка?
(85% + 75%=160%, что на 60% превышает общее число делегатов конференции. За счет чего образовался излишек? За счет тех людей, которые оба языка знают, — их мы посчитали дважды. Таким образом, оба языка знают не менее 60 % делегатов конференции.)
Найдите корни уравнения
а) 1 + х = 2 – х, (0,5)
б) 9х — 4 = 9х + 5, ( ø )
в) 3х + 1 = 3х + 1. (х принадлежит R)
При каких значениях b число 3 является корнем уравнения?
Что значит решить уравнение с параметром? (Под решением уравнения f(x;a)=0
с параметром а будем понимать систему значений х и а из области определения уравнения, обращающую его в верное числовое равенство)
Решите уравнение с параметром:
а) 
б) 
в) 
 .
.- РЕШЕНИЕ ЗАДАЧ
Сегодня мы посвятим урок решению задач с параметром аналитическим и графическим способами.
№1. Решите уравнение:
Если а не равно 0, преобразуем уравнение: а+х = а 2 + ах,
(а — 1) х = — а (а — 1).
а = 1, тогда
х принадлежит R.
3) Если а не равно 1, а <> 0, х = — а.
Для удобства записи ответа сделаем рисунок решений
Ответ: если а = 0, то решений нет, если а = 1, то х– любое число, если а? 0, а? 1, то х=- а.
Дадим геометрическую интерпретацию уравнения

Работа с графиком:
Назовите пары решения уравнения
Например: а = 1, х = 2,
№ 2 Отцу 40 лет. Через сколько лет отец будет в два раза старше сына?
Пусть сыну а лет. Пусть через х лет отец будет в два раза старше сына.
х + 40 (лет) будет отцу, а + х (лет) будет сыну. Т.к. по условию задачи отец будет в два раза старше сына, то 40 + х = 2 (а + х),
По смыслу задачи а >= 0, но 40 — 2 а >= 0, а значит а 0, x + 2 = a или х + 2 = — а,
х = а — 2, х = — а — 2.
Ответ: если a 0, то х1 = а — 2.
2 способ. Графический
Построим в одной системе координат графики функций у = | х + 2| и у = а.
Если a > 0, то у = — х — 2, или у = х + 2,
— х — 2 = а, х + 2 = а,
х = — а — 2; х = а — 2.
Ответ: еслиa 0, то х1 = а — 2.
№ 4 Самостоятельно с последующей проверкой на доске.
При каком значении а уравнение имеет один корень?
а) | х| + | х — а | = — 3,
в) 2| х| + | х — 1| = а.
а) | х| + | х — а | = — 3,
Ответ: при любом а корней нет, т.к. сумма двух неотрицательных чисел есть число неотрицательное.
б) | х| + | х — а | = 0,
Ответ: при а = 0, единственный корень х = 0.
в) 2 | х| + | х — 1 | = а.
Это уравнение решить аналитически трудно. Попробуем решить его графически.
Построим в одной системе координат графики функций: у = 2 | х| + | х — 1 | и у = а.
Если х = 1,y = 2x+x- 1,
Ответ: при а = 1 уравнение имеет единственный корень х = 0.
№ 749 (4) Повторение действий с многочленами. № 737 Текстовая задача.
При каком значении а уравнение 3 | х — 1| + | х — 2| = а не имеет корней?
Необязательное задание: найти натуральное число А, если известно, что из трех данных утверждений два верно, а одно – нет. 1) А + 7 – точный квадрат,
2) последняя цифра А равна 1, 3) А — 8 – точный квадрат.
Аналитические методы решения линейных уравнений с параметрами.
консультация по алгебре (11 класс) на тему
В работа рассмотрены различные подходы к решению линейных уравнений с параметрами.
Скачать:
Вложение Размер parametry.docx 31.82 КБ Предварительный просмотр:
Аналитические методы решения линейных уравнений с параметрами.
В работе рассмотрены различные подходы к решению линейных уравнений с параметрами. Данная тема необходима учащимся для первичного ознакомления с методами решения уравнений с параметрами, которая является опорным пунктом подготовки к ЕГЭ (решение заданий части «С5»).
- Понятие уравнений с параметрами.
- Различные виды и методы решений линейных уравнений с параметрами.
- Задания для самостоятельной работы.
Рассмотрим уравнения, в которых некоторые коэффициенты заданы не конкретными числами, а обозначены буквами. Такие уравнения называются уравнениями с параметрами, а буквы – параметрами. Предполагается, что эти параметры могут принимать любые числовые значения.
Решить уравнение с параметрами – значит, найти множество всех корней данного уравнения в зависимости от допустимого значения параметра. (Т.е. указать, при каких значениях параметра существуют решения, и каковы они, затем исследовать его относительно параметра)
Алгоритм решения уравнений с параметрами примерно таков:
- Разбить область изменения параметра на промежутки, где при изменении параметра в каждом из них полученные уравнения решаются одним и тем же методом.(Границами промежутков служат те значения параметра, в которых, или при переходе через которые, происходит качественное изменение уравнения. Такие значения параметра называют «особыми» или контрольными).
- Отдельно на каждом промежутке находятся корни уравнения, выраженные через значения параметра.
- Ответ уравнения состоит из списков изменения параметра с указанием всех корней для каждого промежутка (или конкретных значений параметра).
Основные методы решения уравнений с параметрами.
- Решение простейших линейных уравнений с параметрами.
Исследуем линейное уравнение вида: ax =b (1)
- а 0, b R, то уравнение (1) имеет единственный корень х= .
- а=0, b=0, уравнение (1) имеет корнем любое действительное число, т.е. х R.
- а 0, 0, уравнение (1) не имеет корней.
Пример №1: ax = 5; при a=0 имеем 0х=5, чего не может быть,
тогда х , при а 0 х= .
Пример №2: 0х=а; при а=0 получим 0х=0 х R, при а 0 х .
Пример №3 : Iхl=а, при а=0 х=0; при а>0 х= а, при а х .
Приведем уравнение к виду: х(а-1)=6;
если а=1, то 0х=6, нет решений;
Ответ: при а 1 х = ; при а=1 нет решений.
- Более сложные линейные уравнения с параметром, при решении которых требуется дополнительная проверка, связанная с ограничением на ОДЗ.
Алгоритм решения таких уравнений:
- Найти ОДЗ.
- Решить уравнение относительно х.
- Определить контрольные значения параметра (к.з.п.)
- Проверить, нет ли таких значений параметра, при которых значение х было бы равно числу, не входящему в ОДЗ.
- ОДЗ: х 2
- К.з.п. а=0.
- Решим уравнение относительно х:
- При а=0 уравнение имеет вид =3. Уравнение корней не имеет.
- При а 0 уравнение имеет вид а=3(х-2), отсюда х=
- Проверим, нет ли таких значений параметра а, при которых х=2, т.е. решим уравнение: =2, а=0 ( т.е. приа=0 нет решений)
Ответ: при а 0 х= ; при а=0 нет решений.
2. Решим уравнение относительно х. Умножим обе части уравнения на а 0: 2(а-1)х=(х-1)а +5;
2ах -2х – ах = 5 – а;
- К.з.п. а = 2, т.к. коэффициент при х обращается в 0 при а=2
- Если а=2, то 0х=3, нет решений;
- Если а 2, то х = .
Ответ: при а=2 нет решений; при а 2 и при а 0 х = ; при а=0 уравнение не имеет смысла.
Примечание. Если при каком-нибудь значении параметра а=а 0 данное уравнение не имеет смысла, то нет и решений при а=а 0. Обратное утверждение не верно. Бывает, что при контрольном значении параметра уравнение имеет корни, но они не входят в ОДЗ.
3.Уравнения, сводящиеся к линейным
Пример №1 Решить уравнение: m = +
- ОДЗ: т 0, х 1.
- Решим уравнение относительно х. Умножим обе части уравнения на т(х-1) 0, получим т 2 (х-1) = х – 1 + т – 1;
Х( т 2 – 1) = т 2 + т – 2;
- К.з.п. т= 1
- Если т=1, то 0х=0, следовательно, х-любое действительное число, где х 1.
- Если т=-1, то 0х=-2, нет решений.
- Если т 1 и т то х= .
- Если т = 0, то нет решений.
- Проверим, нет ли значений параметра а, при которых найденное значение х равно 1:
= 1, т+2=т+1, 0т=1, нет решений.
Ответ: при т=0 и т=-1 нет решений; при т=1 х (-∞;1) (1;+∞); при т 1 и
Пример №2 Решить уравнение: = .
2)Решим уравнение относительно х: (a+b)х = a – b.
3) К.з.п.: a+b = 0, a = -b.
- Если a = -b, то нет решений.
- Если a -b, то х = .
- Найдем значения параметров а и b, при которых полученное значение х=1:
1 = , 2b = 0, b = 0. Следовательно, при b = 0 нет решений.
Ответ: при a -b и b 0 х = ; при a = -b и b=0 нет решений.
Пример №3 (МГУ, 2002) При каких значениях параметра b уравнение
9х+ b 2 – (2 — )b — 2 = b 4 х – b 2 (b + ) не имеет корней?
- ОДЗ: х .
- Решим уравнение относительно х:
(b 4 – 9)х = b 3 + (1+ ) b 2 – (2 — )b -2 ,
Линейное уравнение не имеет корней тогда и только тогда, когда
Первое уравнение системы имеет два корня: b 1 = , b 2 = — .
- Подставим во второе уравнение системы b 1 = , получим: 2 +6 ;
b 2 = — , получим 0=0. Т.е. второму условию удовлетворяет b 1 = .
Ответ: при b= уравнение корней не имеет.
Решить самостоятельно уравнения
1) (а+5)(а-3)х=а 2 — 25 ( при а и а х= ; при а=3 ; при а=-5 х ∊ R)
2) а 2 х = а(х+2) – 2 ( при а и а х= ; при а=0 ∅ ; при а=1 х ∊ R)
3) = — ( при а=-3, а=-2, а=1/2 ∅ ; при а и а х= )
4)1+ = — ( при а и а х= ; при а=-3, а=0, а=1 ∅ )
5) Для каких значений а решение уравнения 10х-15а = 13- 5ах = 2а больше 2? (МГУ, 1982)
- Г.А. Ястребинецкий. Уравнения и неравенства, содержащие параметры. М. Просвещение.1972.
- А.Г. Корянов. Задачи с параметрами. Брянск.2010.
- М.А. Галицкий, А.М.Гольдман, Л.И. Звавич. Сборник задач по алгебре для 8-9 классов. Углубленное изучение математики. М. Просвещение. 1992.
По теме: методические разработки, презентации и конспекты
Рабочая программа элективного курса по математике 10 класс «Методы решения задач с параметром».
Предлагаемый курс «Методы решения задач с параметром» предназначен для реализации в 10 классах для расширения теоретичес.
Координатно-параметрический метод решения задач с параметрами
Решение задач с параметрами систематизирует знание основных разделов школьной математики, повышает уровень математического и логического мышления, формирует первоначальные навыки исследовательской дея.
Аналитические методы решения задач с параметрами Составитель: Е.М .Чернова МКОУ КГ№ 1
Одними из наиболее сложных задач для учащихся в курсе математики — это задачи с параметрами, так как требуют от них умения рассуждать логически и анализировать полученные решения. С одной сторон.
Графические методы решения уравнений с параметрами
урок в 11 классе.
Применение различных способов и методов решения задач с параметрами
Задачи с параметрами являются сложными потому, что не существует единого алгоритма их решения. Спецификой подобных задач является то, что наряду с неизвестными величинами в них фигурируют параметры, ч.
Основные методы решения задач с параметрами
В действующем формате ЕГЭ по математике (профильный уровень) задания №18 содержат параметры и предполагают исследование свойств различных элементарных функций. Поэтому подготовку к и.
Аналитический способ решения задач с параметром.
Данный материал предназначен для обучающихся 10-11 классов и содержит задания для подготовки к ЕГЭ по теме «Задание №18. Решение задач с параметром». Он направлен на совершенствование умений.
Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на
для этого умножим все элементы первого столбца на эту неизвестную:
Второй столбец умножим на
третий столбец — на
-ый столбец — на
и все эти произведения прибавим к первому столбцу, при этом произведение
не изменится:
Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель
называется первым вспомогательным определителем СЛАУ.
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины
Проанализируем полученные формулы:
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку
Отсюда видно, что СЛАУ решена верно.
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных
матpицы-столбцы неизвестных
и свободных коэффициентов
Тогда СЛАУ можно записать в матричном виде
Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу
к матрице А, получим
в силу того, что произведение
найдем
Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу
после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.
Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу
(см. Лекцию № 2): найдем детерминант матрицы А.
Пример:
Решение:
Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу
(в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:
Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим
Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки
Разделим все элементы второй строки на (-5), получим эквивалентную матрицу
Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки
Разделим все элементы третьей строки на (-3), получим
Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной х, второй — при неизвестной у, третий — при неизвестной z, а за вертикальной чертой находится столбец свободных коэффициентов):
Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы
называется наивысший порядок отличного от нуля минора этой матрицы.
Если
то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например,
среди миноров третьего порядка также есть миноры, которые не равны нулю, например,
Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство
для определителей). Следовательно, ранг матрицы А равен 3.
Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
Рекомендую подробно изучить предметы:
- Математика
- Алгебра
- Линейная алгебра
- Векторная алгебра
- Высшая математика
- Дискретная математика
- Математический анализ
- Математическая логика
Ещё лекции с примерами решения и объяснением:
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
источники:http://nsportal.ru/shkola/algebra/library/2015/03/23/analiticheskie-metody-resheniya-lineynyh-uravneniy-s-parametrami
http://www.evkova.org/metodyi-resheniya-sistem-linejnyih-algebraicheskih-uravnenij-slau


















 для этого умножим все элементы первого столбца на эту неизвестную:
для этого умножим все элементы первого столбца на эту неизвестную: 
 третий столбец — на
третий столбец — на  -ый столбец — на
-ый столбец — на  и все эти произведения прибавим к первому столбцу, при этом произведение
и все эти произведения прибавим к первому столбцу, при этом произведение  не изменится:
не изменится:

 называется первым вспомогательным определителем СЛАУ.
называется первым вспомогательным определителем СЛАУ.
 Проанализируем полученные формулы:
Проанализируем полученные формулы: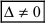 ), то система имеет единственное решение;
), то система имеет единственное решение;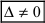 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 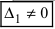 или
или 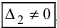 , или, . или
, или, . или 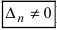 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);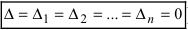 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.




 Отсюда видно, что СЛАУ решена верно.
Отсюда видно, что СЛАУ решена верно. матpицы-столбцы неизвестных
матpицы-столбцы неизвестных  и свободных коэффициентов
и свободных коэффициентов 
 Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу
Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу  к матрице А, получим
к матрице А, получим  в силу того, что произведение
в силу того, что произведение  найдем
найдем  Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу
Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу  после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.
после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.

 (см. Лекцию № 2): найдем детерминант матрицы А.
(см. Лекцию № 2): найдем детерминант матрицы А.

 Запишем обратную матрицу
Запишем обратную матрицу  (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:
(в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:

 Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки
Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки  Разделим все элементы второй строки на (-5), получим эквивалентную матрицу
Разделим все элементы второй строки на (-5), получим эквивалентную матрицу 
 Разделим все элементы третьей строки на (-3), получим
Разделим все элементы третьей строки на (-3), получим  Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной х, второй — при неизвестной у, третий — при неизвестной z, а за вертикальной чертой находится столбец свободных коэффициентов):
Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной х, второй — при неизвестной у, третий — при неизвестной z, а за вертикальной чертой находится столбец свободных коэффициентов):
 называется наивысший порядок отличного от нуля минора этой матрицы.
называется наивысший порядок отличного от нуля минора этой матрицы. то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.
то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.
 среди миноров третьего порядка также есть миноры, которые не равны нулю, например,
среди миноров третьего порядка также есть миноры, которые не равны нулю, например,  Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство
Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство  для определителей). Следовательно, ранг матрицы А равен 3.
для определителей). Следовательно, ранг матрицы А равен 3.