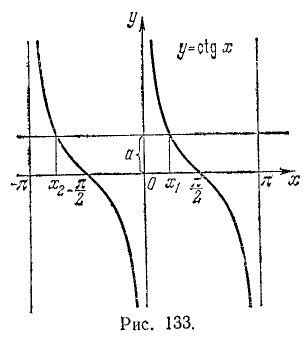
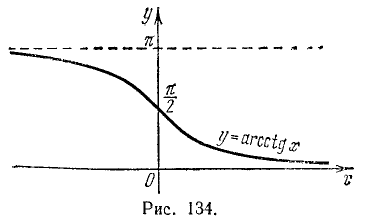
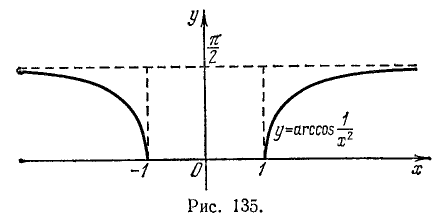
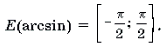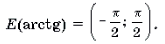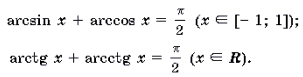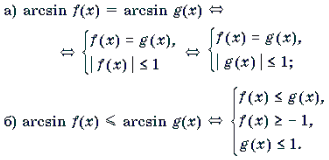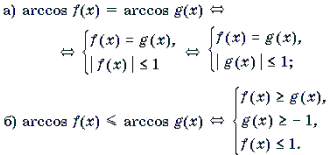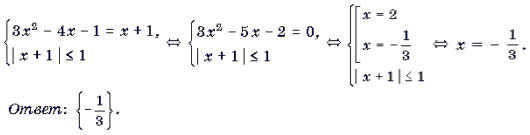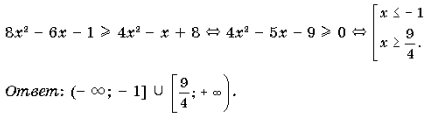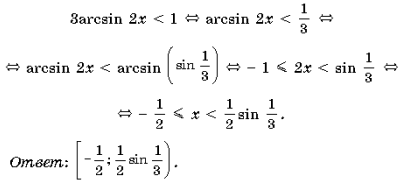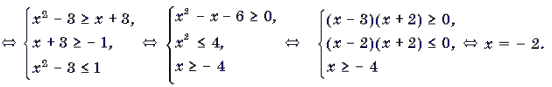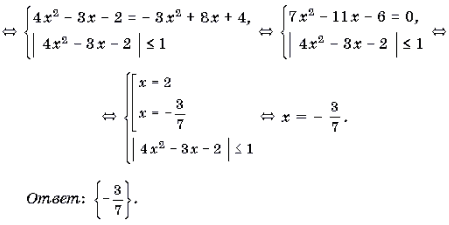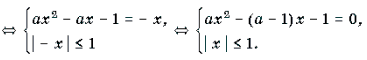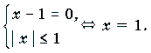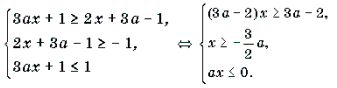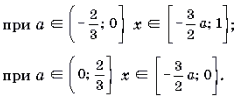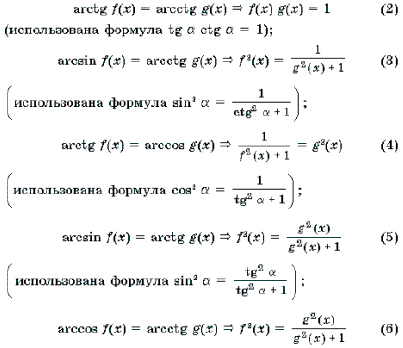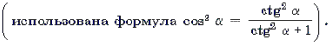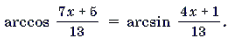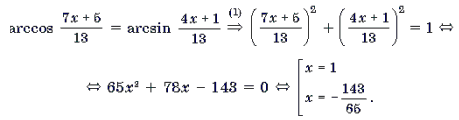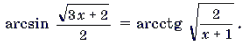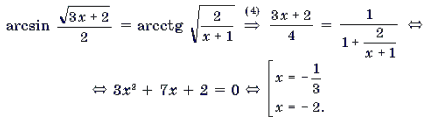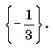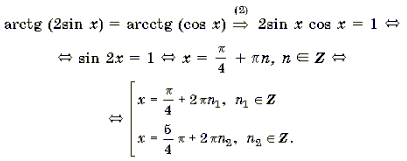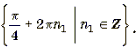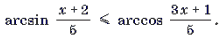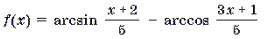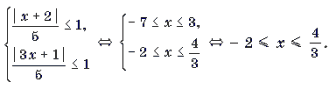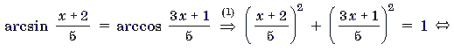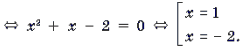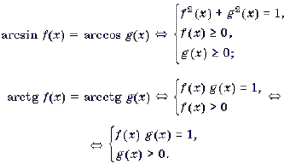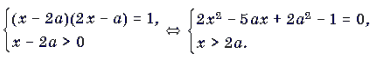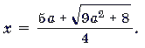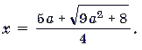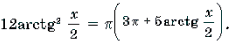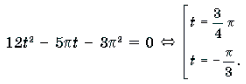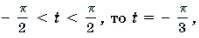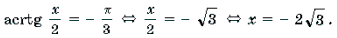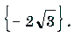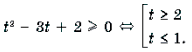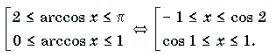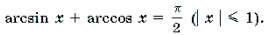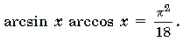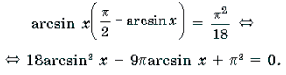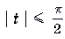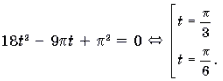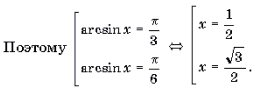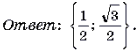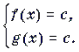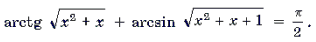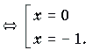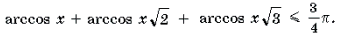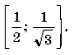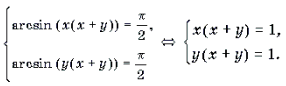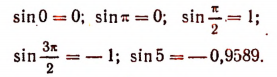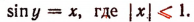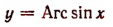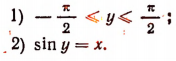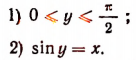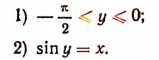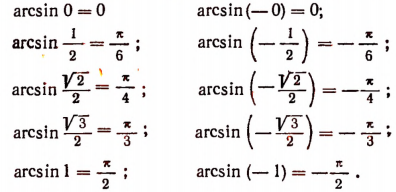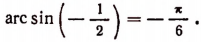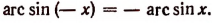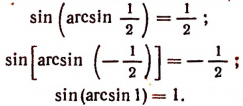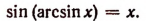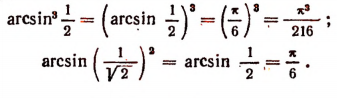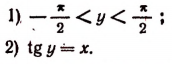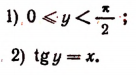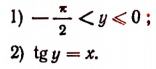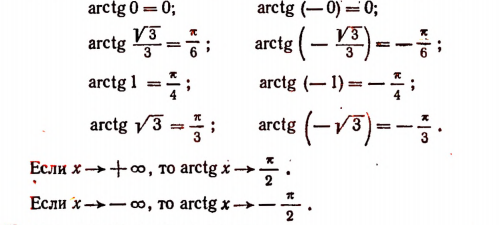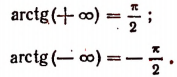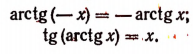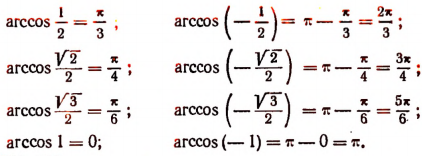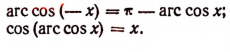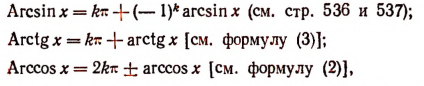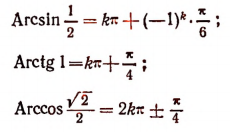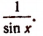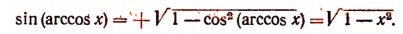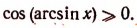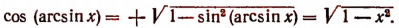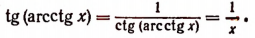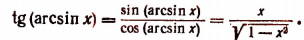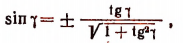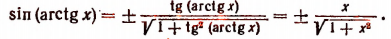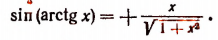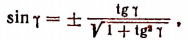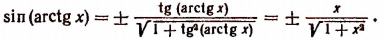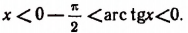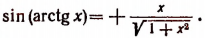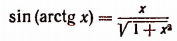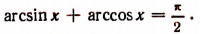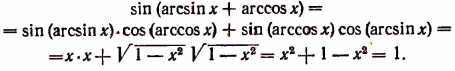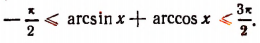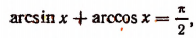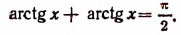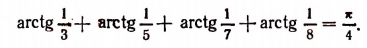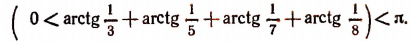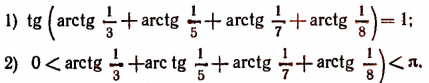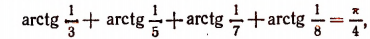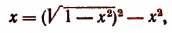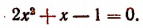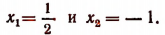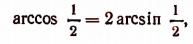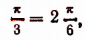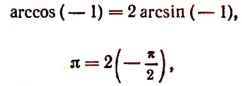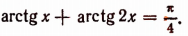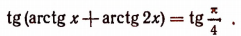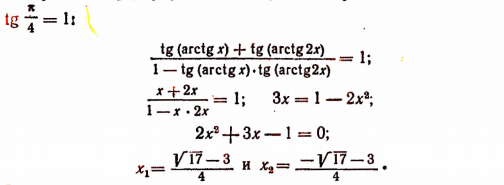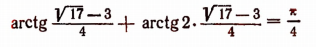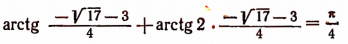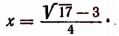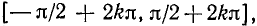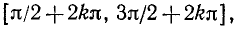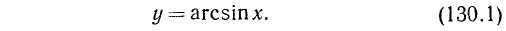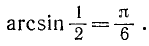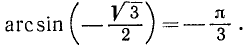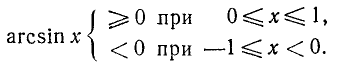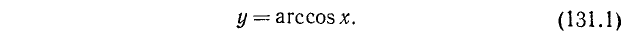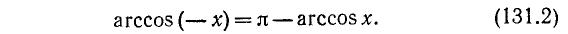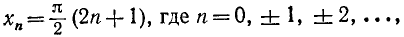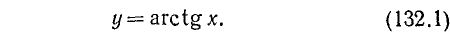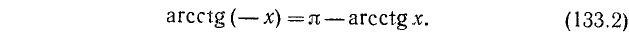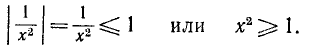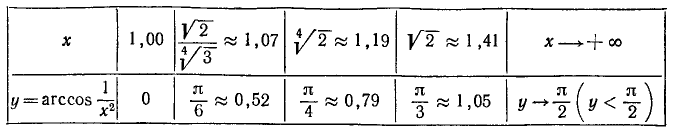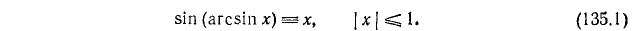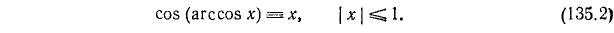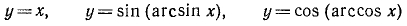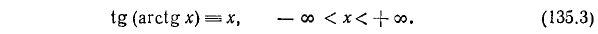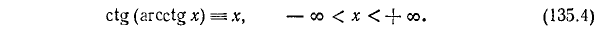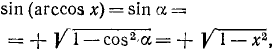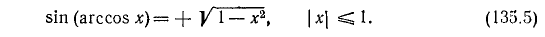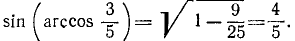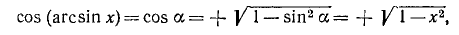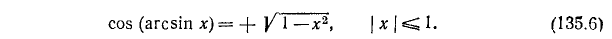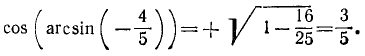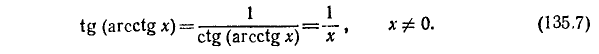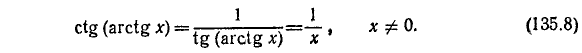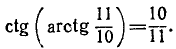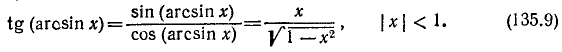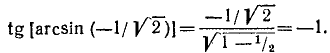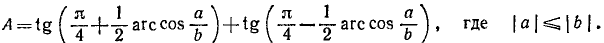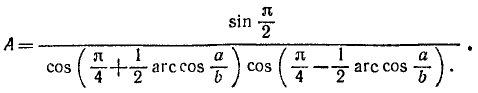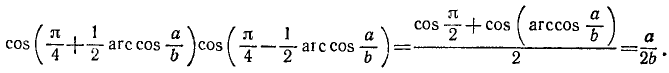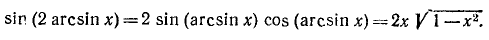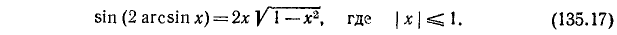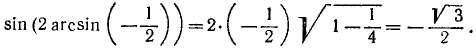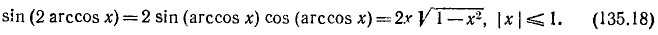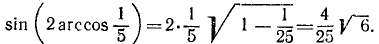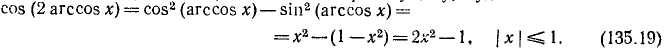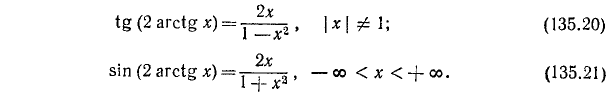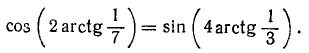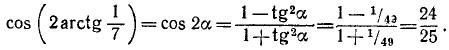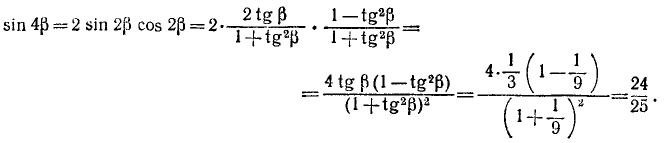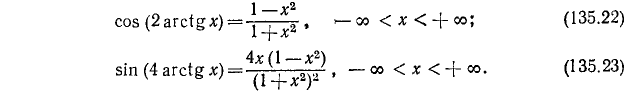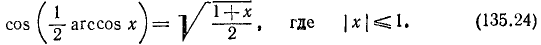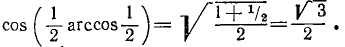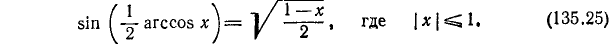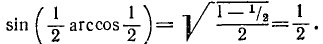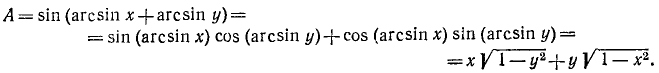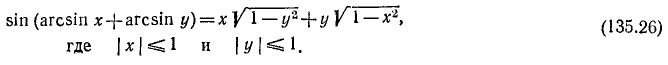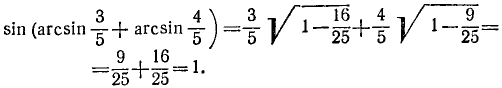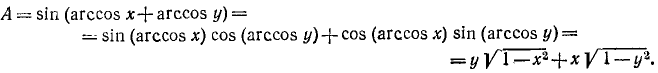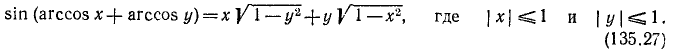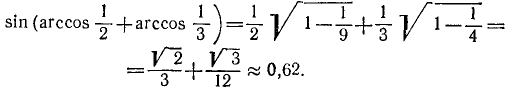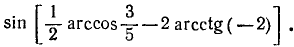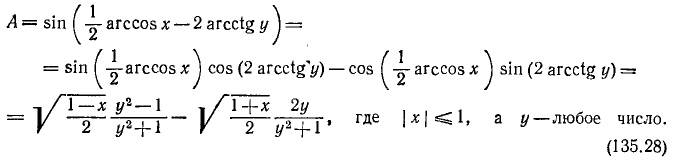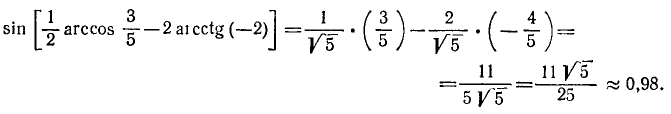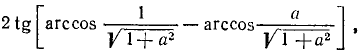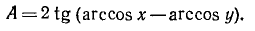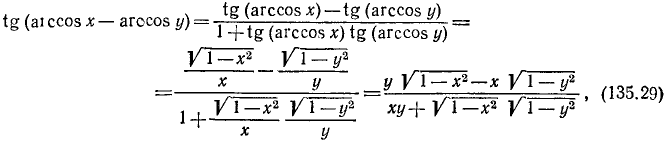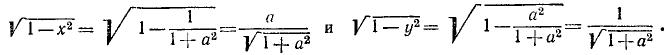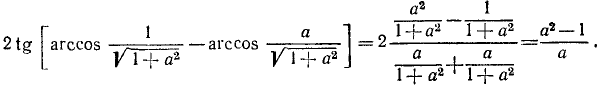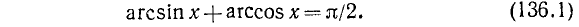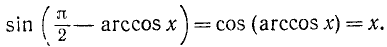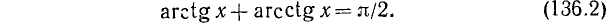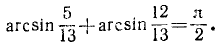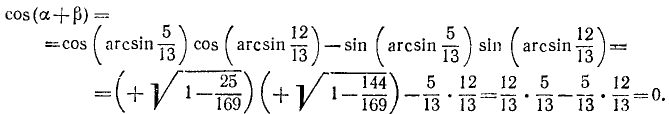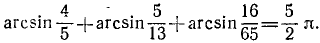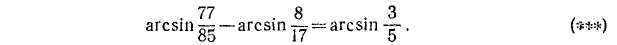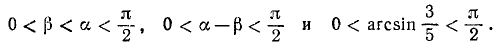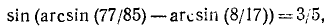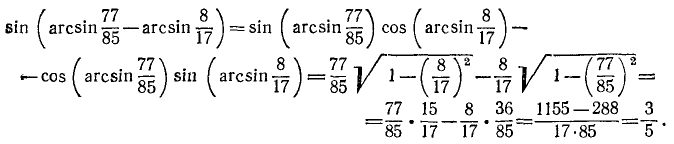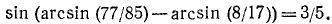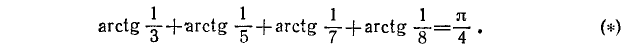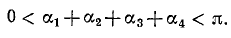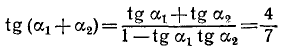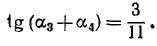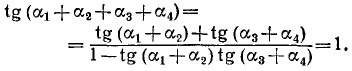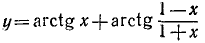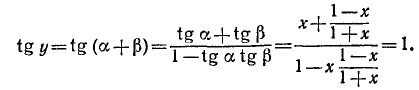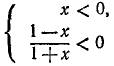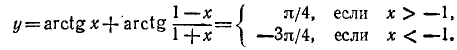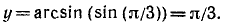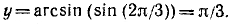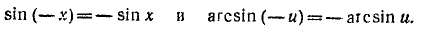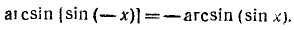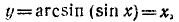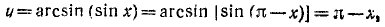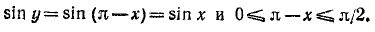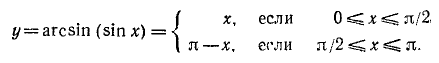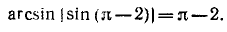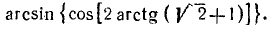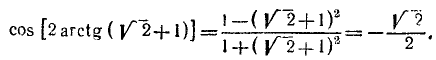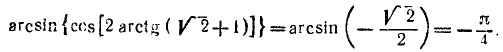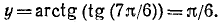Уравнения и неравенства, содержащие обратные тригонометрические функции
Задачи, связанные с обратными тригонометрическими функциями, часто вызывают у школьников старших классов значительные трудности. Связано это, прежде всего, с тем, что в действующих учебниках и учебных пособиях подобным задачам уделяется не слишком большое внимание, и если с задачами на вычисление значений обратных тригонометрических функций учащиеся еще как-то справляются, то уравнения и неравенства, содержащие эти функции, нередко ставят их в тупик. Последнее не удивительно, поскольку практически ни в одном учебнике (включая учебники для классов с углубленным изучением математики) не излагается методика решения даже простейших уравнений и неравенств такого рода. Предлагаемая вашему вниманию статья посвящена методам решения уравнений и неравенств, содержащих обратные тригонометрические функции. Надеемся, что она окажется полезной для учителей, работающих в старших классах – как общеобразовательных, так и математических.
Вначале напомним важнейшие свойства обратных тригонометрических функций.
1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];
arcsin (– x) = – arcsin x (x О [– 1; 1]);
2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];
3 Функция y = arctg x определена и монотонно возрастает на R;
arctg (– x) = – arctg x (x О R);
4 Функция y = arcctg x определена и монотонно убывает на R;
5
Свойства монотонности и ограниченности являются ключевыми при решении многих уравнений и неравенств, содержащих обратные тригонометрические функции. Перейдем к рассмотрению методов решения этих уравнений и неравенств.
I. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями
Решение уравнений и неравенств, левая и правая части которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функций, как монотонность. Напомним, что функции y = arcsin t и y = arctg t монотонно возрастают, а функции y = arccos t и y = arcctg t монотонно убывают на своих областях определения. Поэтому справедливы следующие равносильные переходы.
1 .
2 .
3 .
4 .
Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | Ј 1 (тогда используем первую систему), или | g(x) | Ј 1 (в этом случае используем вторую систему).
Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).
Решение. Уравнение равносильно системе
Замечание 2. Решать неравенство, входящее в систему, вообще говоря, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении примера 1.
Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) Ј arcctg (4x 2 – x + 8).
Решение. Неравенство равносильно следующему:
Пример 3. Решить неравенство 3arcsin 2x
Пример 4. Решить неравенство arccos (x 2 – 3) Ј arccos (x + 3).
Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = p .
Решение. Так как p – arccos t = arccos (– t), то имеет место следующая цепочка равносильных преобразований:
arccos (4x 2 – 3x – 2) = p – arccos (3x 2 – 8x – 4) Ы
Ы arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4) Ы
Аналогичные равносильные преобразования используются и при решении задач с параметрами.
Пример 7. Решить уравнение с параметром a: arcsin (ax 2 – ax + 1) + arcsin x = 0.
Решение. Уравнение равносильно уравнению
Рассмотрим два случая:
1) a = 0. В этом случае система примет вид:
2) a № 0. В этом случае уравнение системы является квадратным. Его корни: 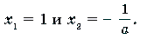
Так как | x | Ј 1, то 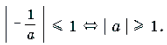
Ответ: при 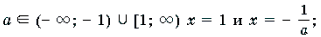
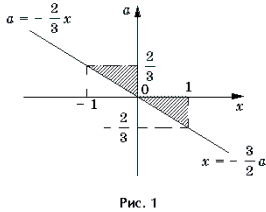
Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) Ј arccos (2x + 3a – 1).
Решение. Неравенство равносильно системе
Решать последнюю систему можно графо-аналитическим методом, учитывая то, что при a > 




II. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями
При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Эта группа задач является чуть более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x0 – решение этого уравнения. Обозначим arcsin f(x0) = arccos g(x0) через a. Тогда sin a = f(x0), cos a = g(x0), откуда f 2 (x0) + g 2 (x0) = 1. Итак, arcsin f(x) = arccos g(x) Ю f 2 (x) + g 2 (x) = 1. (1)
Рассуждая аналогично, можно получить следующие переходы:
Замечание 3. Корнем каждого из уравнений (1)–(4) может быть только такое число x0, для которого f(x0) і 0 и g(x0) і 0. В противном случае множество значений левой и правой частей уравнения не пересекаются.
Пример 9. Решить уравнение
Корень 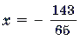
Пример 10. Решить уравнение
Корень x = – 2 является посторонним.
Ответ: .
Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).
Корни вида 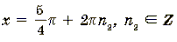
Ответ:
При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в некоторых случаях учитывать свойства монотонных функций.
Пример 12. Решить неравенство
Решение. Рассмотрим функцию
и решим неравенство f(x) Ј 0 методом интервалов.
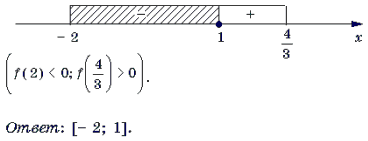
1) Найдем D(f). Для этого решим систему
2) Найдем нули f(x). Для этого решим уравнение
Корень x = – 2 является посторонним.
3) Решим неравенство f(x) Ј 0 методом интервалов.
Замечание 4. Заметим, что найдя корень уравнения 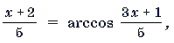

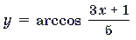
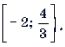
При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например,
Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).
Решение. Данное уравнение равносильно системе
Графиком квадратного трехчлена f(x) = 2x 2 – 5ax + 2a2 – 1 является парабола, ветви которой направлены вверх. Поскольку f(2a) = – 1 2a. Это корень
Ответ: при любом a
III. Замена переменной
Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно свести к алгебраическим, сделав соответствующую замену переменной. При этом следует помнить о естественных ограничениях на вводимую переменную, связанных с ограниченностью обратных тригонометрических функций.
Пример 14. Решить уравнение
Решение. Обозначим 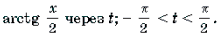
Поскольку
откуда
Ответ:
Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 і 2.
Решение. Пусть arccos x = t, 0 Ј t Ј p . Тогда
Поскольку 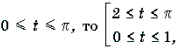
Ответ: [– 1; cos 2] И [cos 1; 1].
Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества
Пример 16. Решить уравнение
Решение. Данное уравнение равносильно следующему:
Пусть arcsin x = t,
Тогда
IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций
Решение некоторых уравнений и неравенств, содержащих обратные тригонометрические функции, основывается исключительно на таких свойствах этих функций, как монотонность и ограниченность. При этом используются следующие теоремы.
Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.
Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.
Теорема 3. Если 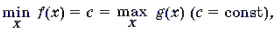
системе
Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.
Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.
Пример 18. Решить уравнение
Решение. Пусть x 2 + x = t. Тогда уравнение примет вид
Функции 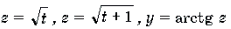
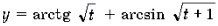
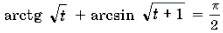
Пример 19. Решить неравенство
Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке 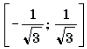
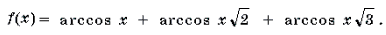
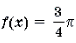
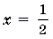
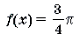
Ответ:
Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = p .
Решение. Поскольку arcsin 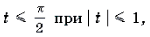
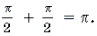
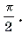
Решение последней системы не представляет труда.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение тригонометрических уравнений.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое уравнение
Решить уравнение
Немного теории.
Тригонометрические уравнения
Уравнение cos(х) = а
Из определения косинуса следует, что \( -1 \leqslant \cos \alpha \leqslant 1 \). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.
Уравнение cos x = а, где \( |a| \leqslant 1 \), имеет на отрезке \( 0 \leqslant x \leqslant \pi \) только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если a
Уравнение sin(х) = а
Из определения синуса следует, что \( -1 \leqslant \sin \alpha \leqslant 1 \). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.
Уравнение sin х = а, где \( |a| \leqslant 1 \), на отрезке \( \left[ -\frac<\pi><2>; \; \frac<\pi> <2>\right] \) имеет только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если а
Уравнение tg(х) = а
Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.
Уравнение tg x = а для любого a имеет на интервале \( \left( -\frac<\pi><2>; \; \frac<\pi> <2>\right) \) только один корень. Если \( |a| \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right) \); если а
Решение тригонометрических уравнений
Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратным
Решить уравнение 2 cos 2 (х) — 5 sin(х) + 1 = 0
Заменяя cos 2 (х) на 1 — sin 2 (х), получаем
2 (1 — sin 2 (х)) — 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) — 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y — 3 = 0, откуда y1 = -3, y2 = 0,5
1) sin(х) = — 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; \( x = (-1)^n \text
Ответ \( x = (-1)^n \frac<\pi> <6>+ \pi n, \; n \in \mathbb
Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) — 4 = 0
Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 — sin 2 (6х)) + 4 sin(6х) — 4 = 0 => 3 sin 2 (6х) — 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 — 4y +1 =0, откуда y1 = 1, y2 = 1/3
Уравнение вида a sin(x) + b cos(x) = c
Решить уравнение 2 sin(x) + cos(x) — 2 = 0
Используя формулы \( \sin(x) = 2\sin\frac
Поделив это уравнение на \( \cos^2 \frac
Обозначая \( \text
В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях \( a \neq 0, \; b \neq 0, \; c \neq 0, \; c^2 \leqslant b^2+c^2 \) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на \( \sqrt
Решить уравнение 4 sin(x) + 3 cos(x) = 5
Здесь a = 4, b = 3, \( \sqrt
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.
Решить уравнение sin(2х) — sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) — sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x — 1) = 0
Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х — х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0
Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) — sin 2 (x), то
cos(2x) = 1 — sin 2 (x) — sin 2 (x), cos(2x) = 1 — 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 — cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 — cos(2x)) + 2 (1 — cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0
Обратные тригонометрические функции в математике с примерами решения и образцами выполнения
Когда задается какое-либо отвлеченное число х и требуется найти sin х, то, как известно, всякий раз для любого определенного значения х мы находим для sin х единственный ответ, а именно некоторое определенное отвлеченное число, заключенное в границах от — 1 до
+ 1 включительно.
Это замечание относится и к каждой из остальных тригонометрических функций. Поэтому все тригонометрические функции sin х , cos х , tg х являются функциями однозначными.
Если же нам будет задано какое-либо отвлеченное число х в границах от — 1 до +1 включительно и будет предложено отыскать такое отвлеченное число у, синус которого равен числу х , то всякий раз будет получаться не один, а бесконечное множество ответов.
Например, если 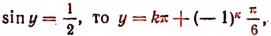
Это замечание относится и к остальным тригонометрическим функциям.
Отсюда следует, что у есть такое отвлеченное число, синус которого равен х. Вместо этого словесного утверждения пишут:
(читают: у равен арксинусу х).
Как уже разъяснялось, выражение Arc sin х для всякого данного значения х, заключенного в границах от — 1 до + 1 включительно, имеет бесконечное множество различных значений.
Приставка Arc неотделима от обозначения sin и вместе с ним образует знак нового математического действия над отвлеченным числом х.
Подобным же образом вводятся математические действия
Arc cos х обозначает такие всевозможные отвлеченные числа, что косинус каждого из них равен х;
Arc tg x обозначает такие всевозможные отвлеченные числа, что тангенс каждого из них равен х (здесь х может быть любым числом).
Выражения Arc sin x, Arc cos х, Arc tg x называются обратными тригонометрическими функциями аргумента х.
Как мы уже видели, все обратные тригонометрические функции являются функциями многозначными (с бесконечным множеством значений). В отличие от обратных тригонометрических функций функции sin x, cos x, tg x и т. д. называются прямыми тригонометрическими функциями аргумента х.
Как уже отмечалось, все прямые тригонометрические функции являются функциями однозначными.
Пользоваться обратными тригонометрическими функциями при решении задач не всегда удобно вследствие их многозначности. Поэтому наряду с обратными тригонометрическими функциями Arc sin х, Arc cos x и т. д. вводятся и изучаются еще и другие обратные тригонометрические функции, а именно
arc sin x, arc cos x, arc tg x,
которые определяются так, чтобы каждая из них была функцией однозначной.
Свойства однозначных обратных тригонометрических функций
A. arc sin х
arc sin x есть отвлеченное число в границах от — 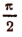
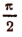
Из этого определения следует, что равенство у = arc sin х равносильно следующим утверждениям:
Если 0
Если —1
Значение функции arc sin x представляет собой определенное действительное число лишь в том случае, когда
i*i
Чтобы найти, например, 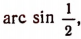
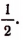
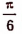
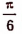
Чтобы найти 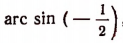
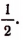
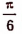
Очевидно, что
Этот результат легко обобщить и получить, что
Нетрудно убедиться, что, например,
Из определения функции arcsin х следует, что
Если над числом х сначала выполняется действие нахождения арксинуса, а затем над полученным результатом действие нахождения синуса, то в результате получится первоначальное число х.
Выражение 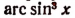
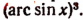
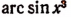
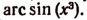
Б. arctg x
arctg х есть отвлеченное число в границах от — 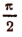
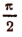
Из этого определения следует, что равенство у = arctg х равносильно следующим утверждениям:
Если то равенство у = arctg х равносильно следующим утверждениям:
Если х
Значение функции arctg х представляет собой определенное действительное число при всяком значении х.
Из данного определения функции arctg х следует, что
Поэтому иногда условно пишут:
B. arccos x
arccos х есть отвлеченное число в границах от 0 до равное числу радианов, содержащихся в таком угле, косинус которого равен х.
Равенство у = arccos х равносильно следующему:
Значение функции arccos х представляет определенное действительное число тогда и только тогда, когда |х|
Выражения многозначных обратных тригонометрических функций
Многозначные обратные тригонометрические функции выражаются формулами:
где k — любое целое число (положительное, отрицательное или нуль).
Функция y = Arcsin х называется функцией, обратной функции у = sinх. Функция же csc х не есть функция, обратная функции sin х, но есть величина, обратная величине sin х, так как csc х =
Из многозначной функции Arcsin х можно выделить сколько угодно однозначных функций. Например, можно выделить однозначную функцию, заключающуюся в границах от 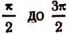
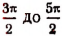
Но во всех теоретических и практических вопросах принято пользоваться преимущественно однозначной функцией арксинуса в границах от— 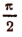
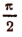
О знаках математических действий
Напишем знаки известных нам математических действий:
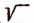
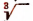
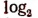
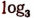
sin — знак синуса;
cos — знак косинуса;
arc sin — знак арксинуса (однозначного);
arc tg — знак арктангенса (однозначного);
Arcsin — знак арксинуса (многозначного);
Arc tg — знак арктангенса (многозначного).
Если под каждым из этих знаков поместить какое-либо число, например число 100, то получим:


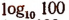
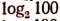

sin 100 — синус числа 100;
cos 100 — косинус числа 100;
arc sin 100 — арксинус (однозначный) числа 100;
arc tg 100 — арктангенс (однозначный) числа 100;
Arc sin 100—арксинус (многозначный) числа 100;
Arc tg 100 — арктангенс (многозначный) числа 100.
Любое из этих математических действий выполняется над отвлеченным числом и в результате опять получается отвлеченное число. Всякое математическое действие выполняется по своему особому правилу.
Пользуясь тем, что эти правила нам известны, мы получим:

Выражаясь образно, можно сказать, что каждый знак математического действия представляет собой как бы простейшую математическую «машину», принимающую к переработке отвлеченные числа. В то время как некоторые из этих «машин» принимают к переработке любые числа, другие принимают не всякие числа.
Например, «машины» 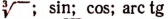
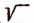
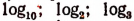
Полученное в результате математических действий число может выражать ту или иную физическую величину в зависимости от той конкретной задачи, которую мы решали с помощью этих математических действий.
Примеры преобразований и вычислений, связанных с однозначными обратными тригонометрическими функциями
1. Упростить выражение sin (arccos х).
Так как 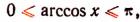
Поэтому, пользуясь формулой 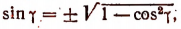
2. Упростить выражение cos (arcsin х).
Так как 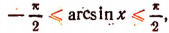
Поэтому, пользуясь формулой 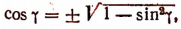
3. Упростить выражение tg (arcctgx).
Пользуясь формулой 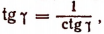
4. Упростить выражение tg (arcsin х).
Пользуясь формулой 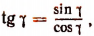
5. Упростить выражение sin (arctg х).
Пусть 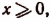
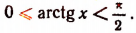
Но из этих двух знаков годным является только знак плюс. Действительно, 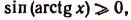
Правая же часть будет положительным числом или нулем, если из двух знаков, стоящих перед ней, выбрать только знак плюс (ведь по условию 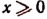
Пусть х
Но из этих двух знаков годным является только знак плюс. Действительно, 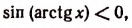
Правая же часть будет отрицательным числом лишь тогда, когда мы из двух знаков, стоящих перед ней, выберем только знак плюс (ведь по условию х
Таким образом, равенство
справедливо при всяком значении х.
6. Доказать тождество
Сначала вычислим синус левой части написанного выше равенства:
Из одного того факта, что sin (arcsin х + arccos х) = 1, мы еще не можем заключить, что 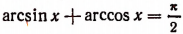
Чтобы удостовериться в том, что сумма arcsin х + arccos х равняется именно 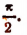
Но среди чисел, больших или равных — 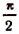
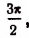
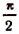
что и требовалось доказать.
Аналогично доказывается и тождество
7. Показать справедливость равенства
Сначала вычислим тангенс суммы, стоящей в левой части написанного равенства:
Для сокращения записей вычислим предварительно значения тангенсов, стоящих в числителе последней дроби:
Найдем также, что
Складывая, получим, что
Итак, мы установили два факта:
Из этих двух фактов вытекает, что
что и требовалось доказать.
8. Решить уравнение arccos х = 2arcsin x.
Если два числа равны, то равны и их косинусы. Поэтому из данного уравнения вытекает уравнение cos (arccos х) = cos(2 arcsin x). Но данное уравнение и вновь полученное, вообще говоря, не равносильны. Всякий корень первого уравнения будет корнем второго, но не всякий корень второго уравнения обязательно должен быть корнем первого, так как из равенства косинусов не обязательно следует равенство чисел, стоящих под знаками косинусов. Поэтому каждый из корней второго уравнения надо испытать подстановкой в первое уравнение и отобрать лишь те, которые удовлетворяют первому уравнению.
Второе уравнение после преобразований примет вид:
Подставляя в первоначально заданное уравнение вместо неизвестного х число 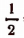
Подставляя число — 1, получим:
т. е. равенство неверное.
Итак, первоначальное уравнение имеет лишь один корень х =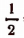
9. Решить уравнение
Преобразуем данное уравнение, взяв тангенсы его левой и правой части:
(см. пояснения к примеру 8).’
Применим формулу тангенса суммы и примем во внимание, что
справедливо, так как его левая часть заключена между 0 и 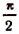
несправедливо, так как его левая часть заключена между — 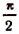
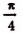
Следовательно, данное уравнение имеет только один корень
Графики обратных тригонометрических функций
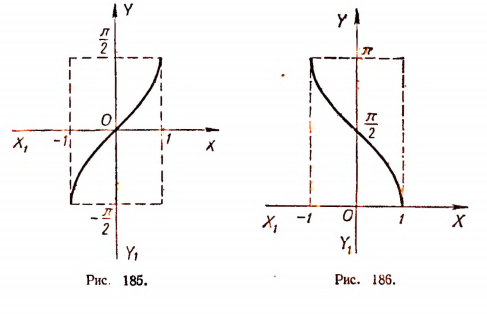
На рисунке 185 изображен график функции у = arcsin х.
На рисунке 186 изображен график функции у = arccos х.
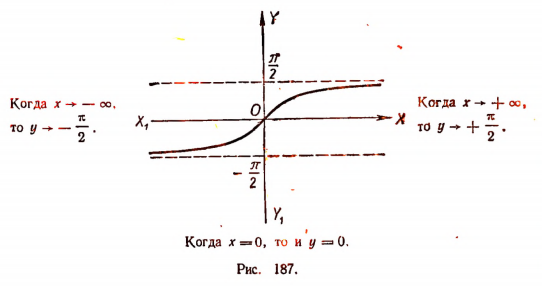
На рисунке 187 изображен график функции у = arctg х.
Дополнение к обратным тригонометрическим функциям

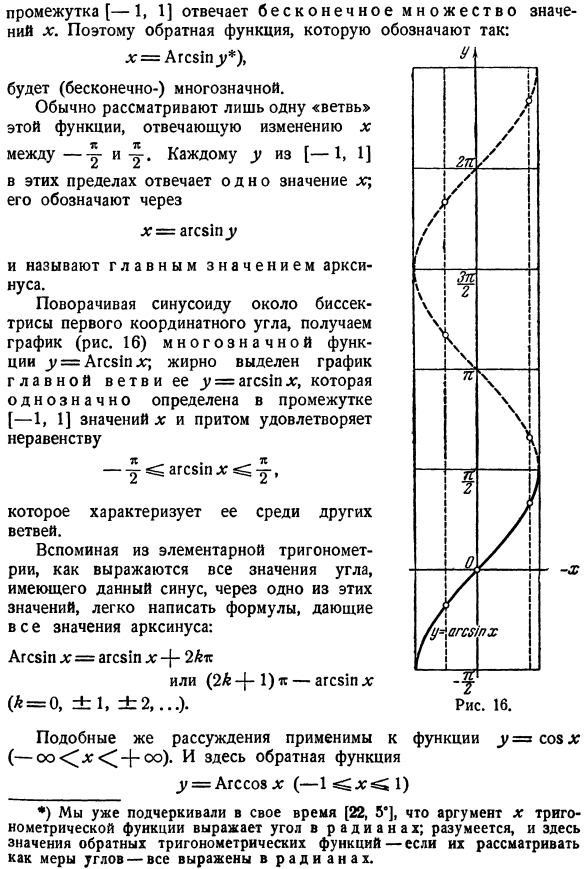
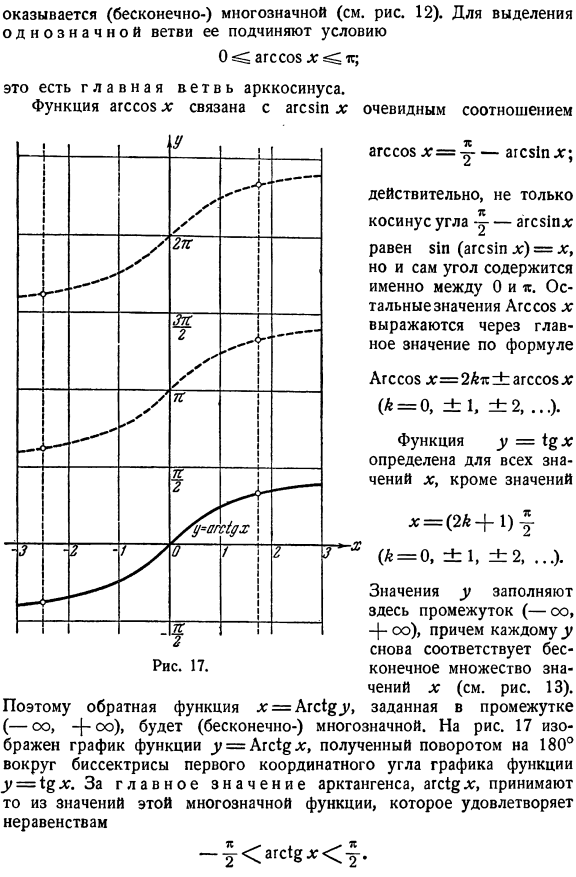


Обратные тригонометрические функции и их графики
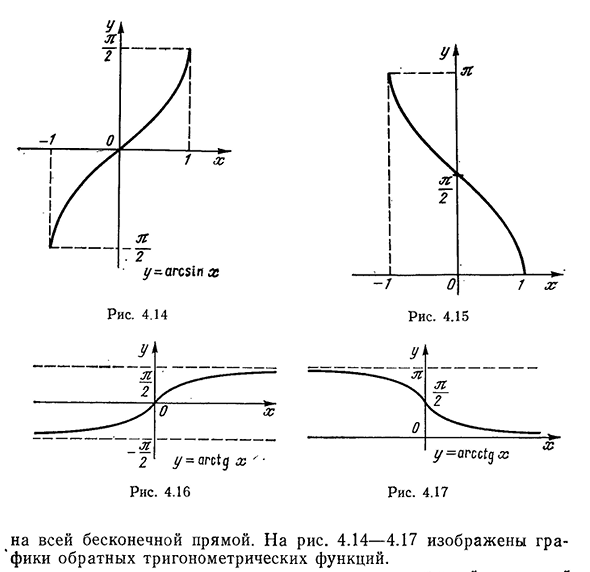
Функция y = arcsin x (арксинус).
Рассмотрим функцию y = sin x. Так как область определения этой функции — вся ось Ох (
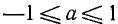
бесконечно много значений аргумента 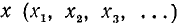
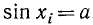
Для того чтобы получить обратную (однозначную) функцию к функции у = sin x, достаточно рассмотреть какой-либо наибольший отрезок оси Ох, на котором функция y = sin x или монотонно возрастает, или монотонно убывает (см. п. 35). Функция у = sin х монотонно возрастает от —1 до +1, например, на отрезке 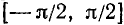
где k = 0, ±1, ±2,… Она монотонно убывает от +1 до —1 на любом отрезке вида
где k = 0, ±1, ±2, …
На всей оси Ох функция y = sin x обратной (однозначной) функции не имеет. На каждом же из отрезков монотонности функция y = sin x имеет обратную функцию. Остается теперь зафиксировать какой-либо из этих отрезков. В качестве отрезка оси Ох, на котором рассматривается функция у = sin x и обратная к ней функция, обычно берут отрезок 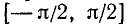
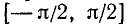
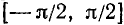
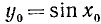
Пример:
Найти а = arcsin (1/2).
Данный пример подробно можно сформулировать так: найти такой аргумент а, лежащий в пределах от 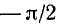
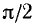
Решение:
Существует бесчисленное множество аргументов, синус которых равен 1/2, например: 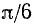
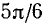
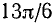
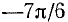
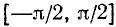
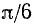
Пример:
Найти 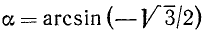
Решение:
Рассуждая так же, как и в примере 1, получим
По общему правилу (см. п. 35) график обратной функции симметричен с графиком основной функции относительно биссектрисы I—III координатных углов (рис. 21).
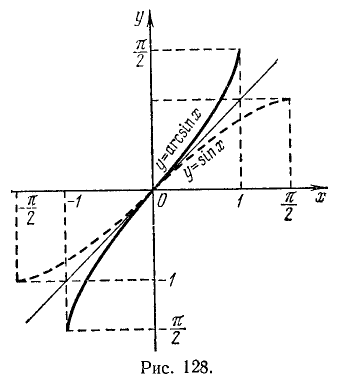
Свойства функции у = arcsin х (рис. 128).
1) Область определения: отрезок [—1, 1].
2) Область изменения: отрезок 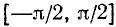
3) Функция у = arcsin х нечетная: arcsin (—x) = — arcsin х.
4) Функция y = arcsin х монотонно возрастающая.
5) График пересекает оси Ох, Оу в начале координат.
Перечисленные свойства вытекают из свойств функции у = sin x на отрезке 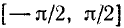
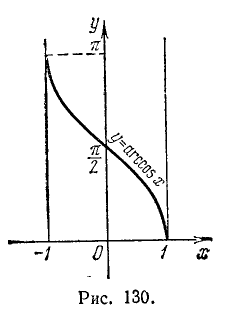
Функция y = arccos x (арккосинус)
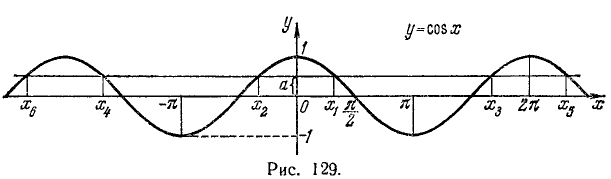
Функция у = cos x определена на всей оси Ох (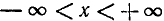
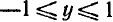
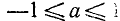
На рис. 129 видно, что существует бесконечно много значений аргумента х (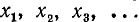
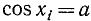
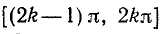
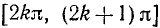
В качестве отрезка оси Ох, на котором рассматривается функция у = cos x и обратная к ней функция, обычно берут отрезок 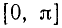
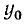
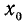
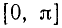
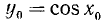
Пример:
Найти 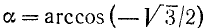
Подробно данный пример можно сформулировать так: найти такой аргумент а, лежащий в пределах от 0 до 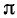
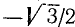
Решение:
Существует бесчисленное множество аргументов, косинус которых равен 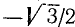
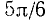
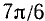
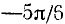
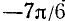
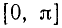
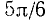
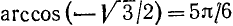
Пример:
Найти 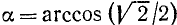
Решение:
Рассуждая так же, как и в предыдущем случае, мы получим 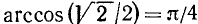
График функции у = arccos х симметричен с графиком функции у = cos x относительно биссектрисы I—III координатных углов (см. рис. 21 в п. 35).
Свойства функции у = arccos х вытекают из соответствующих свойств функции у = cos x на отрезке 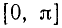
Перечислим эти свойства:
1) Область определения: отрезок [-1, 1].
2) Область изменения: отрезок 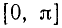
3) Функция у = arccos х ни четная, ни нечетная. Для нее выполняется тождество
4) Функция у = arccos х монотонно убывающая.
5) График пересекает ось Ох в точке (1, 0), а ось Оу в точке 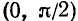
6) 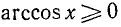
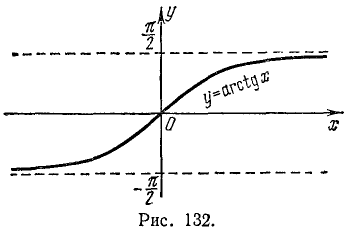
Функция y = arctg x (арктангенс)
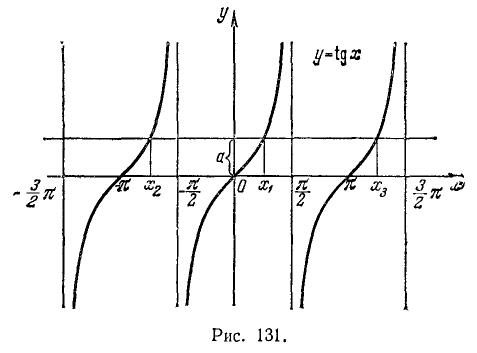
Рассмотрим функцию y = tg x. Область определения этой функции — вся ось Ох, за исключением точек вида
и область изменения значений — вся ось Оу. Об обратной функции (по отношению к функции у = tg x) можно уже говорить для всей оси Оу. Задача нахождения х из уравнения tg х = а и здесь имеет бесчисленное множество решений. На рис. 131 видно, что существует бесконечно много значений аргумента 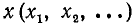
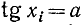
Для того чтобы получить обратную (однозначную) функцию к функции y = tg x, достаточно рассмотреть какой-либо наибольший интервал оси Ох, на котором она монотонно возрастает. Функция у= tg x монотонно возрастает от 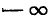
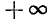
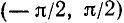
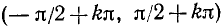
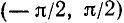
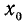
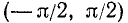
Пример:
Найти 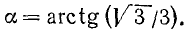
Подробно данный пример можно сформулировать так: найти такой аргумент а, лежащий в пределах от 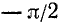
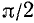
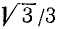
Решение:
Существует бесчисленное множество аргументов, тангенс которых равен 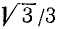
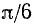
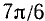
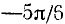
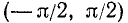
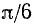
Пример:
Найти 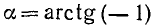
Решение:
Рассуждая так же, как и в предыдущем случае, мы получим 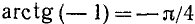
График функции у = arctg х симметричен с графиком функции y = tg x относительно биссектрисы I — III координатных углов (см. рис. 21 в п. 35).
Свойства функции у = arctg x вытекают из соответствующих свойств функции y = tg x на интервале 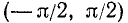
Перечислим эти свойства:
1) Область определения: x — любое действительное число.
2) Область изменения: интервал 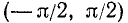
3) Функция y = arctg х нечетная: arctg ( —x) =— arctg x.
4) Функция у = arctg x монотонно возрастающая.
5) График пересекает оси Ох, Оу в начале координат.
6) arctg x 0 при 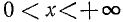
7) Прямые 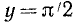

Функция y = arcctg x (арккотангенс)
Функция y = ctg x определена на всей оси Ох, за исключением точек вида 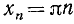
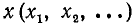
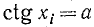
В качестве интервала оси Ох, на котором определяется обратная функция по отношению к функции у = ctg x, берут обычно интервал 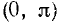
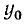
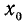
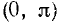
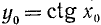
Пример:
Найти 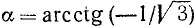
Подробно данный пример можно сформулировать так: найти такой аргумент а, лежащий в пределах от 0 до 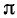
Решение:
Существует бесчисленное множество аргументов, котангенс которых равен 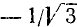
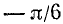
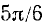
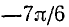
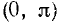
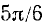
Пример:
Найти а = arcctg 1.
Решение:
Рассуждая так же, как и в предыдущем случае, мы получим 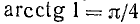
График функции у = arcctg x симметричен с графиком функции у = ctg x относительно углов (см. рис. 21 в п. 35). Свойства функции y = arcctg x вытекают из соответствующих свойств функции y = ctg x на интервале 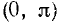
Перечислим эти свойства:
1) Область определения: х — любое действительное число.
2) Область изменения: интервал 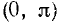
3) Функция у = arcctg х ни четная и ни нечетная. Для нее выполняется тождество
4) Функция у = arcctg x монотонно убывающая.
5) График пересекает ось Оу в точке 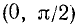
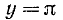
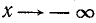
6) arcctg x > 0 при любых х.
Пример:
Построим график функции 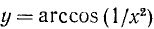
1) Область определения: функция определена для х, удовлетворяющих неравенству
Последнее неравенство удовлетворяется при 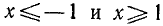
2) Область изменения значений функции: 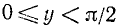
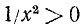
3) Функция четная, так как 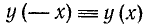
4) Точки пересечения с осями координат:
а) с осью Оу (х = 0) функция не может иметь точек пересечения, так как она определена только при 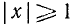
б) с осыо Ох (у = 0) она пересекается в точках (—1, 0) и (1, 0) (нули функции), так как 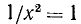
5) Наименьшее и наибольшее значения функции в области определения. В силу четности функции достаточно ее исследовать для 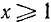
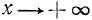
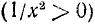
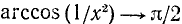
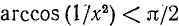
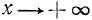
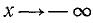
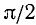
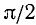
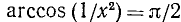
6) Интервалы знакопостоянства: функция всюду в области определения неотрицательна, т. е. 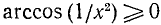
Для построения графика функции найдем некоторые опорные его точки, а затем соединим их плавной линией с учетом свойств функции.
Так как функция 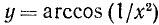
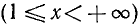
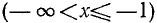
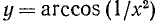
Соединив полученные опорные точки плавной линией и учтя, что прямая 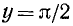
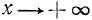
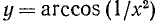
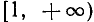
Продолжив его четным образом на бесконечный полуинтервал 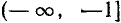
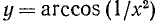
Операции над обратными тригонометрическими функциями
Тригонометрические операции: Рассмотрим некоторые простейшие тригонометрические операции над обратными тригонометрическими функциями (первая группа формул).
1) y= sin (arcsin х). По определению
Пример 1. sin (arcsin 0,93) = 0,93.
2) у = cos (arccos х). По определению
Пример:
cos [arccos (— 0,79)] = — 0,79.
Следует подчеркнуть, что тождества (135.1) и (135.2) справедливы только в области определения (существования) арксинуса и арккосинуса, т. е. при 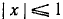
На основании предыдущего заметим также, что функции
совпадают только в области определения арксинуса и арккосинуса, т. е. на отрезке [—1, 1] оси Ох. Вне этого отрезка последние две функции просто не существуют.
3) y = tg (arctg х). По определению
Пример:
tg (arctg 123) = 123.
4) y = ctg (arcctg x). По определению
Пример:
ctg [arcctg (— 987)] = — 987.
Функции y = x, y =tg (arctg x), у = ctg (arcctg x) совпадают на всей оси Ox.
5) у = sin (arccos x). Положив arccos x = a, получим cos a = x.
На основании формулы (100.3) будем иметь
Мы взяли перед корнем знак « + » потому, что а = arccos х удовлетворяет неравенствам 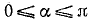
Пример:
6) у = cos (arcsin x). Положив arcsin x = а, получим sin a = x. На основании формулы (100.1) будем иметь
Мы взяли перед корнем знак « + » потому, что угол а = arcsin х удовлетво-ряет неравенствам 
Пример:
7) На основании тождества tg а = 1 /ctg а имеем
Пример:
tg (arcctg (1/9)) = 9.
8) Ha основании тождества ctg a = 1/tg a имеем
Пример:
9) На основании формулы 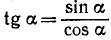
Пример:
Аналогично предыдущему, можно доказать следующие формулы:
Пример:
Решение:
На основании формулы (125.5) имеем
Знаменатель этой дроби преобразуем по формуле (123.2):
Окончательно найдем: А = 2b/а.
С помощью формул (135.1)—(135.16) получим ряд новых соотношений (вторая группа формул).
10) у = sin (2 arcsin х).
Обозначив arcsin x через а, будем иметь sin 2а = 2 sin а cos а, откуда
Мы воспользовались формулами (135.1) и (135.6). Итак,
Пример:
11) у = sin (2 arccos x). Имеем
Пример:
12) у = cos (2 arccos x). Аналогично предыдущему, будем иметь
Есть другие возможные случаи, аналогичные случаям 10) —12), можно вывести соответствующие формулы. Например:
Пример:
Решение:
Вычислим левую и правую части предполагаемого равенства. Обозначим arctg (1/7) через а, тогда tg a = 1/7. Далее, воспользовавшись формулой (122.2), получим
Обозначим arctg (1/3) через 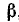
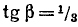
Следовательно, cos (2 arctg (1/7)) = sin (4 arctg (1/3)). Решая пример 13, мы попутно вывели еще две формулы:
Выведем теперь некоторые формулы для тригонометрических функций от половины обратной тригонометрической функции (третья группа формул).
13) 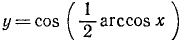
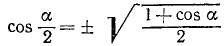
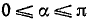
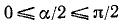
Пример:
14) 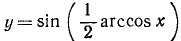
Пример:
Используя формулы сложения и полученные выше формулы, выведем еще ряд соотношений (четвертая группа формул).
15) А = sin (arcsin + arcsin у). На основании формул (116.1), (135.1) и (135.6) будем иметь
Пример:
16) А = sin (arccos x + arccos у). На основании формул (116.1), (135.5) и (135.2) будем иметь
Пример:
В этой группе формул можно образовать очень много различных соотношений. Запоминать все эти формулы не имеет смысла. В дальнейшем при решении примеров мы в каждом конкретном случае будем выводить ту или иную формулу.
Пример:
Решение:
В общем виде наш пример можно записать так:
На основании формул (116.2), (135.24), (135.25), (135.21) и (135.22) будем иметь
В нашем конкретном случае x = 3/5 и у = —2. Следовательно,
Пример:
где a > 0.
Решение:
В общем виде наш пример можно записать так:
На основании формул (117.3) и (135.12) будем иметь
где 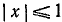
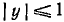
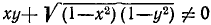
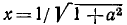
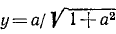
Операции сложения (вычитания)
Выведем теперь некоторые соотношения между обратными тригонометрическими функциями.
Теорема:
Для всех х из отрезка [—1, 1] имеет место тождество
Доказательство:
По определению 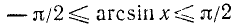
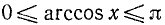
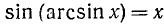
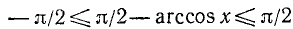
Итак, аргументы arcsin x и 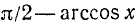
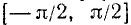
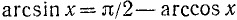
Теорема:
Для всех 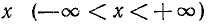
Тождество (136.2) доказывается так же, как и тождество (136.1). Рекомендуем читателю провести это доказательство самостоятельно.
Аналогично предыдущему могут быть получены формулы для arcsin х + arcsin у, arccos x + arccos у, arctg х + arctg у и т. д. Мы не будем их выводить, а приведем ряд примеров, на которых покажем метод решения таких задач.
Пример:
Проверить, имеет ли место равенство
Решение:
Обозначим 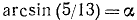
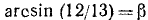
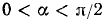
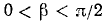
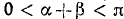
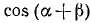
Итак, 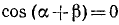
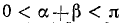
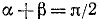
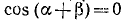
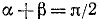
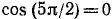
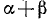
Пример:
Проверить, имеет ли место равенство
Решение:
Обозначим 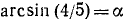
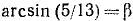
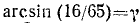
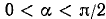
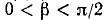
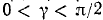
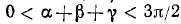
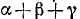
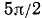
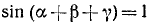
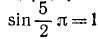
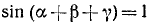
Итак, 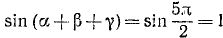
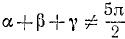
Пример:
Проверить, имеет ли место равенство
Решение:
На основании формулы (131.2)
Предполагаемое равенство (*) перейдет в равенство
Воспользовавшись формулой (136.1), получим
Обозначим 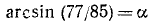
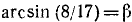
Если мы докажем теперь, что
то будет доказано равенство (**), а тем самым и предполагаемое равенство ():
Следовательно, справедливо и равенство (*).
Пример:
Решение:
Обозначим 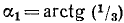
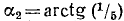
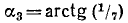
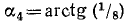
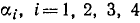
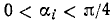
Если нам удастся доказать теперь, что 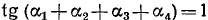
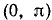
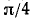
Следовательно, равенство (*) имеет место.
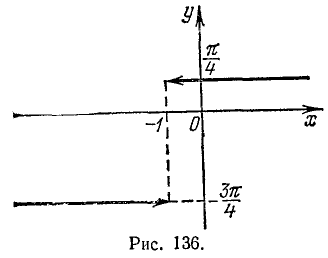
Пример:
и построить ее график.
Решение:
Функция определена всюду, кроме х =—1. Обозначим 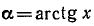
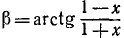
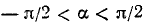
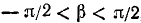
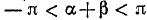
Итак, мы имеем 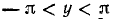
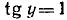
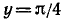
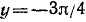
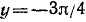
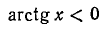
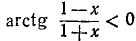
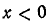
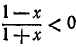
удовлетворяется, если 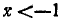

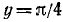
График исследуемой функции изображен на рис. 136.
Обратные тригонометрические операции над тригонометрическими функциями
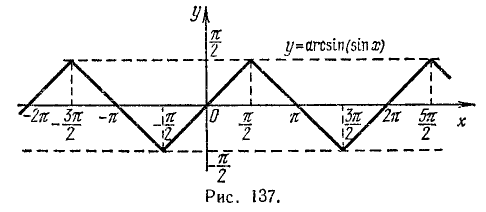
Функция у = arcsin (sin x)
Исследуем функцию y =arcsin (sin х) и построим ее график.
1) Область определения (существования): функция определена для всех x 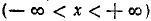
2) Область изменения функции: из определения арксинуса следует, что 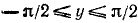
3) Сформулируем словесно правило, определяющее у по заданному х: каждому значению аргумента х 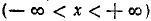
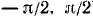
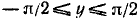
Пример:
Здесь 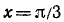
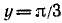
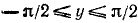
Пример:
Здесь 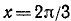
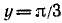
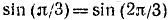
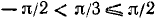
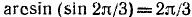
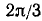
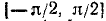
4) Функция нечетна. В самом деле.
5) Функция периодическая с периодом 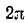
6) График функции y = arcsin (sin х) на отрезке 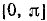
а) При 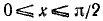
б) При 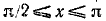
Построив график функции у = arcsin (sin х) на отрезке [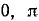
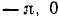
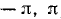
Пример:
Найти а = arcsin (sin 2).
Решение:
Требуется найти угол а, лежащий в пределах от 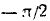
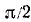
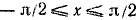
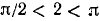
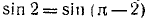

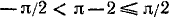
Следовательно, 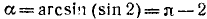
Пример:
Решение:
Воспользовавшись формулой 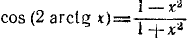
После этого получим
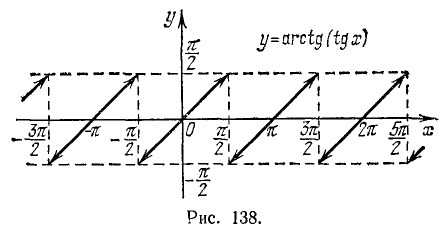
138. Функция y = arctg (tg x). Исследуем функцию y = arctg (tg x) и построим ее график.
1) Область определения (существования): функция определена для всех x, за исключением 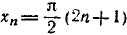
2) Область изменения функции: из определения арктангенса следует, что 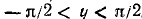
3) Каждому значению х из области определения данной функции ставшей в соответствие значение функции и находящееся в интервале (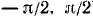
Пример:
y= aictg (tg (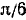
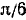
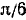
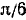
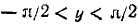
Пример:
Здесь 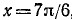
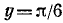
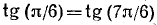
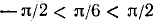
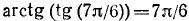
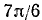
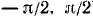
4) Функция нечетна, так как tg (—x) = — tg x и arctg(—u) = — arctg u. Следовательно, arctg (tg (—x)] = — arctg (tg x).
5) Функция периодична с периодом 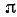
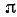
6) График функции y = arctg (tg x) на интервале 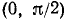
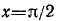
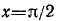
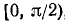
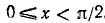
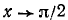
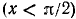
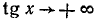
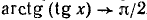
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://www.math-solution.ru/math-task/trigonometry-equality
http://lfirmal.com/obratnye-trigonometricheskie-funkcii/