Арккотангенс решение уравнения ctgx a

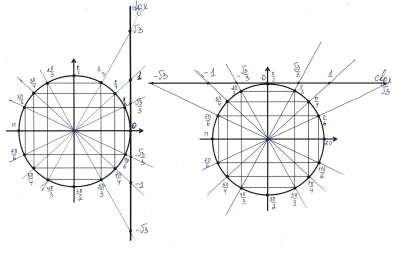
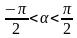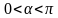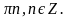Урок «Арктангенс и арккотангенс. Решение уравнений tgx = а, ctgx = a»

Краткое описание документа:

Ранее по программе учащиеся получили представление о решении тригонометрических уравнений, ознакомились с понятиями арккосинуса и арксинуса, примерами решений уравнений cos t = a и sin t = a. В этом видеоуроке рассмотрим решение уравнений tg x = a и ctg x = a.

В начале изучения данной темы рассмотрим уравнения tg x = 3 и tg x = – 3. Если уравнение tg x = 3 будем решать с помощью графика, то увидим, что пересечение графиков функций y = tg x и y = 3 имеет бесконечное множество решений, где x = x₁ + πk. Значение x₁ – это координата x точки пересечения графиков функций y = tg x и y = 3. Автор вводит понятие арктангенса: arctg 3 это число, tg которого равен 3, и это число принадлежит интервалу от –π/2 до π/2. Используя понятие арктангенса, решение уравнения tg x = 3 можно записать в виде x = arctg 3 + πk.

По аналогии решается уравнение tg x = – 3. По построенным графикам функций y = tg x и y = – 3 видно, что точки пересечения графиков, а следовательно, и решениями уравнений, будет x = x₂ + πk. С помощью арктангенса решение можно записать как x = arctg (– 3) + πk. На следующем рисунке увидим, что arctg (– 3) = – arctg 3.

Общее определение арктангенса выглядит следующим образом: арктангенсом а называется такое число из промежутка от –π/2 до π/2, тангенс которого равен а. Тогда решением уравнения tg x = a является x = arctg a + πk.

Автор приводит пример 1. Найти решение выражения arctg.Введем обозначения: арктангенс числа равен x, тогда tg x будет равен данному числу, где x принадлежит отрезку от –π/2 до π/2. Как в примерах в предыдущих темах, воспользуемся таблицей значений. По этой таблице тангенсу данного числа соответствует значение x = π/3. Запишем решение уравнения арктангенс заданного числа равен π/3, π/3 принадлежит и интервалу от –π/2 до π/2.

Пример 2 – вычислить арктангенс отрицательного числа. Используя равенство arctg (– a) = – arctg a, введем значение x. Аналогично примеру 2 запишем значение x, которое принадлежит отрезку от –π/2 до π/2. По таблице значений найдем, что x = π/3, следовательно, -– tg x = – π/3. Ответом уравнения будет – π/3.

Рассмотрим пример 3. Решим уравнение tg x = 1. Запишем, что x = arctg 1 + πk. В таблице значению tg 1 соответствует значение x = π/4, следовательно, arctg 1 = π/4. Подставим это значение в исходную формулу x и запишем ответ x = π/4 + πk.

Пример 4: вычислить tg x = – 4,1. В данном случае x = arctg (– 4,1) + πk. Т.к. найти значение arctg в данном случае нет возможности, ответ будет выглядеть как x = arctg (– 4,1) + πk.

Арккотангенс и решение уравнения ctg x=a (продолжение)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы продолжим изучение арккотангенса и решение уравнений вида ctg x = a для любого а. В начале урока решим уравнение с табличным значением и проиллюстрируем решение на графике, а потом и на круге. Далее решим уравнение ctgt = a в общем виде и выведем общую формулу ответа. Проиллюстрируем вычисления на графике и на круге и рассмотрим различные формы записи ответа. В конце урока решим несколько типовых уравнений и задач с арккотангенсом.

Урок_16_Уравнения вида ctgx=a и tgx=a

Вводится понятие арктангенса и арккотангенса.

Просмотр содержимого документа
«Инструкция к Уроку_16_Уравнения»

Инструкция к Уроку_16 по теме:

«Решение простейших тригонометрических уравнений»

Изучите новый материал и сделайте записи в тетрадь.

Арктангенсом числа a є R называется такое число α є (— 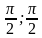), тангенс которого равен а. arctga = α , если tgα = a и

Арккотангенсом числа a є R называется такое число α є (0 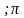), котангенс которого равен а. arcctga = α , если ctgα = a и

Внимание! Ограничения для числа а нет. Оно может принимать любое значение.

arctg(-a) = — arctga acctg(-a) = 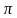– arcctga

1 способ решения простейших уравнений.

x = arctg1 +

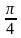
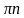
x = + , n є Z.

arctg 1 =

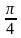
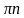
На единичной окружности значению 1 в первой четверти соответствуют угол . Периодом является , где n є Z .

Решением уравнения является формула, в которой содержится множество корней этого уравнения.

x = arctg а +

x = arctg(-1) +

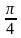
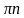
x = — + , n є Z.

arctg (- 1) = – arctg 1 = —

Решением уравнения является формула, в которой содержится множество корней этого уравнения.

x = arctg (- а) +

x = — arctg а +

x = arcctg1 +

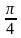
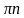
x = + , n є Z.

arcctg 1 =

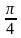
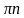
На единичной окружности значению 1 в первой четверти соответствуют угол . Периодом является , где n є Z .

Решением уравнения является формула, в которой содержится множество корней этого уравнения.

x = arcctg а +

x = arcctg(-1) +

x = — )+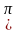

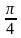
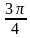
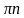
x = + , n є Z.

arcctg (- 1) = 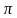– arctg 1 =

Решением уравнения является формула, в которой содержится множество корней этого уравнения.

x = arcctg (- а) +

x =( 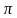— arctg а ) +

2 способ решения простейших уравнений.

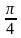
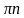
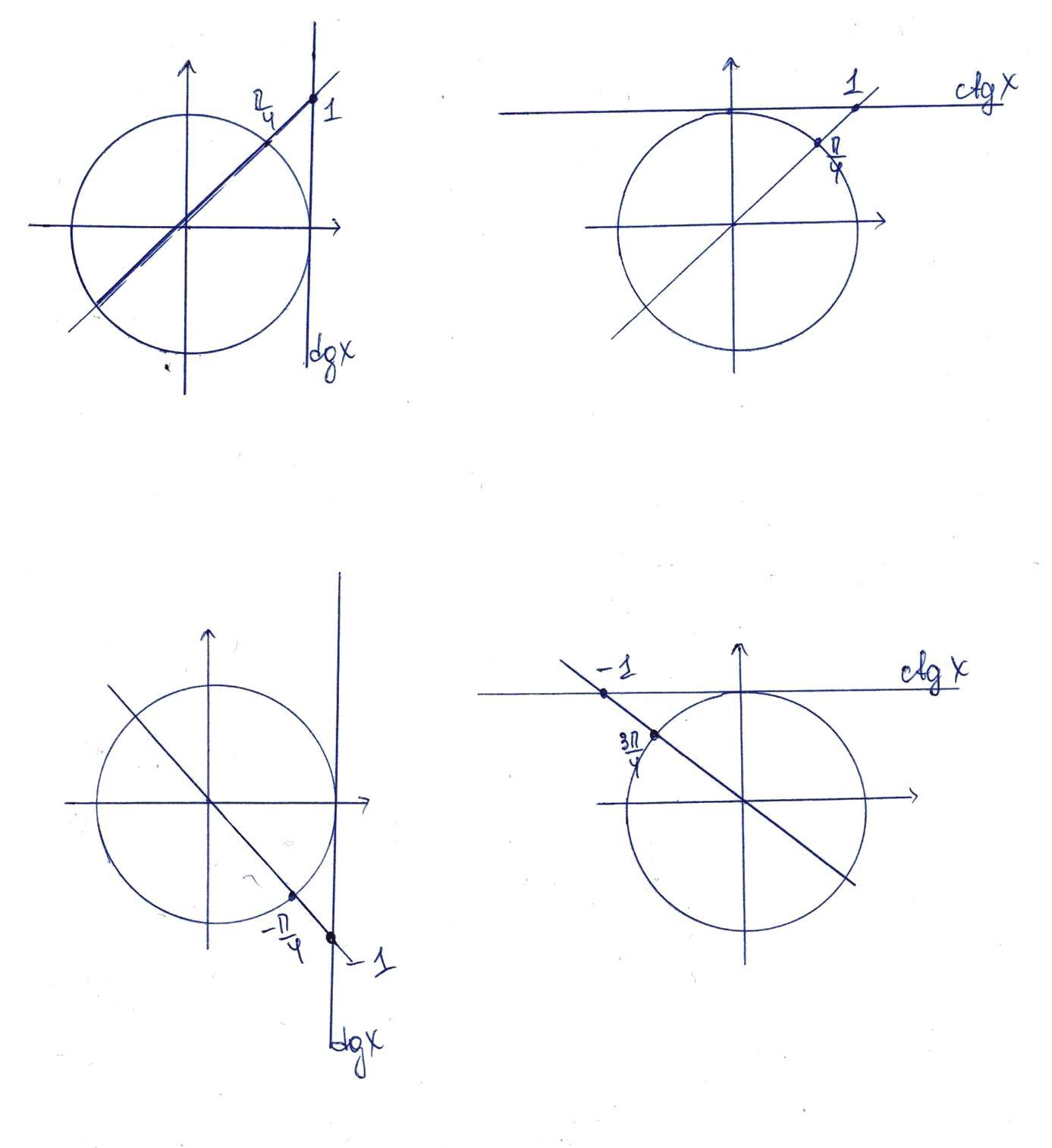
x = + , n є Z .

1. Записываем уравнение.

2. Строим маленькую единичную окружность.

3. Строим ось тангенсов.

4.Отмечаем на ней искомое значение. В данном случае 1.

5. Проводим прямую линию через начало координат.

6. Отмечаем точки.

7. Подписываем радианную меру.

8. Записываем корни уравнения.

x = — + , n є Z.

1. Записываем уравнение.

2. Строим маленькую единичную окружность.

3. Строим ось тангенсов.

4. Отмечаем на ней искомое значение. В данном случае -1.

5. Проводим прямую линию через начало координат.

6. Отмечаем точки.

7. Подписываем радианную меру.

8. Записываем корни уравнения.

x = + , n є Z.

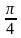
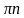
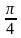
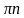
1. Записываем уравнение.

2. Строим маленькую единичную окружность.

3. Строим ось котангенсов.

4. Отмечаем на ней искомое значение. В данном случае 1.

5. Проводим прямую линию через начало координат.

6. Отмечаем точки.

7. Подписываем радианную меру.

8. Записываем корни уравнения.

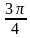
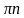
x = + , n є Z.

1. Записываем уравнение.

2. Строим маленькую единичную окружность.

3. Строим ось котангенсов.

4. Отмечаем на ней искомое значение. В данном случае — 1.

5. Проводим прямую линию через начало координат.

6. Отмечаем точки.

7. Подписываем радианную меру.

8. Записываем корни уравнения.

Решите в тетради одним из изученных способов № 41, 42, 43 на стр. 322.

Проверьте решённые номера с помощью файла «Урок_16_Самороверка».

Разобрать оба способа решения уравнений. Выучить материал.

Внимание! За праздничные дни, к 11 мая, решить вариант ЕГЭ (база).

Вариант прикреплен к уроку. Задание обязательно для всех.