Арксинус решение уравнения sint a видеоурок

Урок «Арксинус. Решение уравнения sint = a»

Краткое описание документа:

Аналогично теме в предыдущем видеоуроке рассмотрим уравнение sin t = a и его решение.

Рассмотрим пример – решение уравнения sin t =0,2. Используя числовую окружность на плоскости, найдем, что t₁ и t₂ – это длины дуг AM и AN соответственно. Значит, t = t₁ + 2πk и t = t₂ + 2πk.Найдем, что t₂ = π – t₁. Таким образом, arcsin 0,2 – это число (длина дуги АМ), синус которого равен 0,2, и это число принадлежит первой четверти числовой окружности, т.е. отрезку от 0 до π /2. Тогда корнями уравнения будут t = arcsin 0,2 + 2πk и t = π arcsin 0,2 +2πk.

Далее автор возвращается к понятию единичной числовой окружности. На окружности отмечена точка А. Поставим точку на окружности, которая будет соответствовать каждому действительному числу t в случаях: если t > 0, t n arcsin a + πn, где n – все действительные числа.

Помимо решения равенств, мы также можем решать тригонометрические неравенства. В качестве примера решим неравенство sin t 2 t + cos 2 t = 1, вычислим, что cos (arcsin 5/13) =12/13.

Арксинус. Решение уравнения sint = a.

Рассмотрим, как решаются уравнения с помощью числовой окружности.

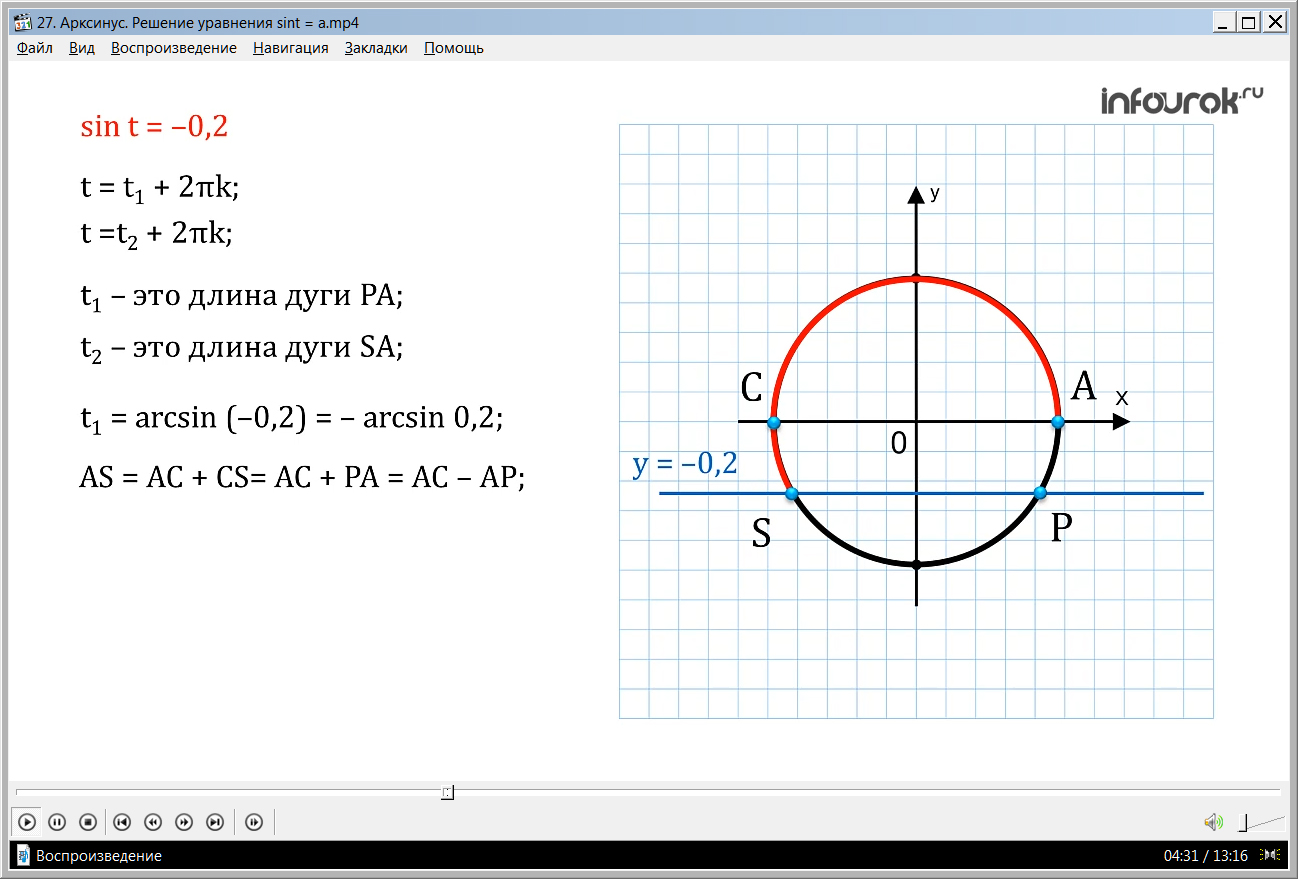
Решим уравнения sint = 0,2 и sint = — 0,2.

Решение первого уравнения будет

t =t₁ + 2πk; t =t₂ + 2πk, где t₁ – это длина дуги АМ, а t₂ – это длина дуги АN.

Так как NC = АМ и АN=АС –NC, АС =π, то t₂ = π — t_1.

По аналогии с арккосинусом математики ввели для числа t₁ новый символ: arcsin 0,2( арксинус ноль целых двух десятых). arcsin 0,2 мы будем понимать как число (длина дуги АМ), синус которого равен 0,2 и которое принадлежит первой четверти числовой окружности (т.е. отрезку [ 0;]).

Тогда корни уравнения sint = 0,2 можно записать в виде:

t = arcsin 0,2 + 2πk;

t =π — arcsin 0,2 + 2πk.

Вспомним определение единичной окружности

ОПРЕДЕЛЕНИЕ Дана единичная окружность, на ней отмечена начальная точка А – правый конец горизонтального диаметра. Поставим в соответствие каждому действительному числу t (тэ) точку окружности по следующему правилу:

1) Если t>0(тэ больше нуля), то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь АМ (а эм) длины t. Точка М и будет искомой точкой М(t) (эм от тэ).

2) Если t n ()+ πn =(– 1) n ∙( — 1) ∙ + πn = (–1) n +1 ·+ πn,

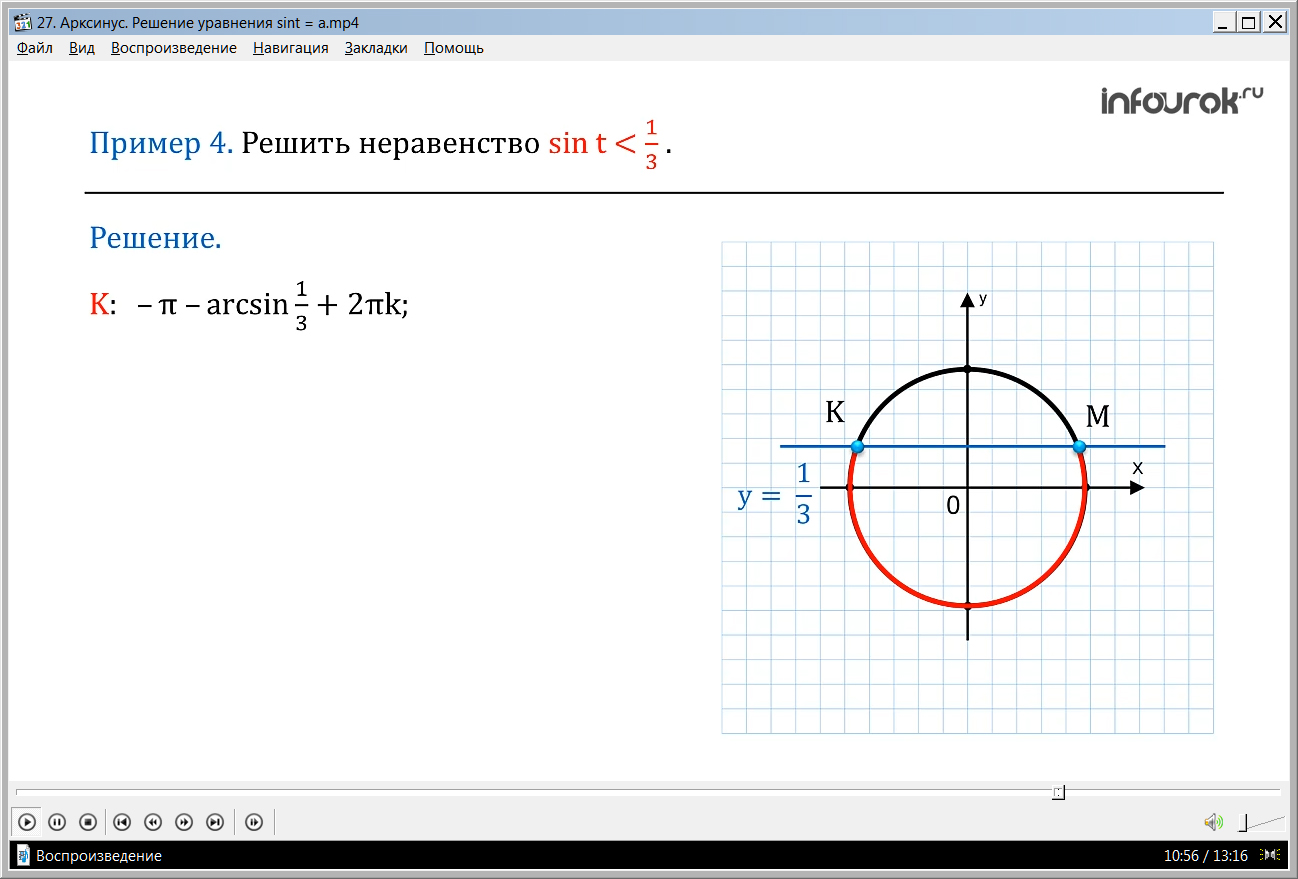
ПРИМЕР 4. Решить неравенство sint .

Решение. Вспомним, что sint – это ордината точки М(t), которая лежит на числовой окружности. То есть нам надо найти такие точки М(t)этой окружности, которые удовлетворяет неравенству у .

Прямая у пересекает числовую окружность в двух точках М и К. Неравенству у соответствуют точки открытой дуги КМ. Точке К соответствует — π – arcsin +2πk (минус пи минус арксинус одной третьей плюс два пи ка), а точке М arcsin +2πk (арксинус одной третьей плюс два пи ка). Следовательно, решение неравенства запишем в виде:

— π – arcsin +2πk t arcsin +2πk ( тэ больше, чем минус пи минус арксинус одной третьей плюс два пи ка, но меньше, чем арксинус одной третьей плюс два пи ка).

ПРИМЕР 5. Вычислить sin( arcsin ) ( синус арксинуса трех шестнадцатых).

Решение. Воспользуемся определением арксинуса. Пусть arcsin = t, тогда sint = , причем tϵ [;. Получили sin (arcsin)= sint =.

ПРИМЕР 6. Вычислить cos(arcsin) (косинус арксинуса пяти тринадцатых).

Решение. Пусть arcsin = t, тогда sint = , причем tϵ[0; ].

Используя основное тригонометрическое тождество (sin 2 t + cos 2 t = 1), выразим значение cos 2 t:

cos 2 t = 1- sin 2 t, т.к. sin 2 t =) 2 ; тогда cos 2 t = 1 — ;выполним вычисления и получим cos 2 t = ; извлечем квадратный корень cost = или cost = –

Так как tϵ[0; ]. ( тэ принадлежит первой четверти), то косинус положительный, т.е. cos(arcsin).

Арксинус и решение уравнения sin t =a

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы продолжим изучение арксинуса и решение уравнений вида sin t = a. В начале урока решим уравнение с нетабличным значением и рассмотрим решение на числовой окружности и на графике. Далее выведем общую формулу ответа для уравнения sin t = a, рассмотрим различные формы записи ответа и рассмотрим некоторые важные частные случаи решения. В конце урока решим несколько более сложных уравнений.

Арксинус. Решение простейших уравнений с синусом. Часть 2

Арксинусом числа \(a\) (\(a∈[-1;1]\)) называют число \(x∈[-\frac<π><2>;\frac<π><2>]\) синус которого равен \(a\) т.е.

Проще говоря, арксинус обратен синусу.

На круге это выглядит так:

Как вычислить арксинус?

Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от \(-\frac<π><2>\) до \(\frac<π><2>\) ) равен аргументу арксинуса?

Например, вычислите значение арксинуса:

а) Синус какого числа равен \(-\frac<1><2>\)? Или в более точной формулировке можно спросить так: если \(\sin ⁡x=-\frac<1><2>\), то чему равен \(x\)? Причем, обратите внимание, нам нужно такое значение, которое лежит между \(-\frac<π><2>\) и \(\frac<π><2>\). Ответ очевиден:

б) Синус какого числа равен \(\frac<\sqrt<3>><2>\)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ \(\frac<π><3>\).

в) Синус от чего равен \(-1\)?
Иначе говоря, \(\sin ⁡x=-1\), \(x=\) ?

Тригонометрический круг со всеми стандартными арксинусами:

Зачем нужен арксинус? Решение уравнения \(\sin x=a\)

Чтобы понять зачем придумали арксинус, давайте решим уравнение: \(\sin ⁡x=\frac<1><2>\).

Это не вызывает затруднений:

Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.

А теперь решите уравнение: \(\sin ⁡x=\frac<1><3>\).

Что тут будет ответом? Не \(\frac<π><6>\), не \(\frac<π><4>\), даже не \(\frac<π><7>\) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?

Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin⁡\frac<1><3>\), потому что известно, что синус равен \(\frac<1><3>\). Длина дуги от \(0\) до правой точки тогда тоже будет равна \(\arcsin⁡\frac<1><3>\). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному \(\arcsin⁡\frac<1><3>\) от \(π\), то её значение составляет \(π- \arcsin⁡\frac<1><3>\).

Ок, значение этих двух точек нашли. Теперь запишем полный ответ: \( \left[ \beginx=\arcsin \frac<1><3>+2πn, n∈Z\\ x=π-\arcsin \frac<1><3>+2πl, l∈Z\end\right.\) Без арксинусов решить уравнение \(\sin ⁡x=\frac<1><3>\) не получилось бы. Как и уравнение \(\sin ⁡x=0,125\), \(\sin ⁡x=-\frac<1><9>\), \(\sin⁡ x=\frac<1><\sqrt<3>>\) и многие другие. Фактически без арксинуса мы можем решать только \(9\) простейших уравнений с синусом:

С арксинусом – бесконечное количество.

Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac<1><\sqrt<3>>\).
Решение:

Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac<1><\sqrt<2>>\).

Решение:
Кто поторопился написать ответ \( \left[ \beginx=\arcsin \frac<1><\sqrt<2>>+2πn, n∈Z\\ x=π-\arcsin \frac<1><\sqrt<2>>+2πl, l∈Z\end\right.\), тот на ЕГЭ потеряет 2 балла. Дело в том, что в отличии от прошлых примеров \(\arcsin⁡ \frac<1><\sqrt<2>>\) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента. Для этого умножим и числитель и знаменатель дробь на корень из двух \(\frac<1><\sqrt<2>> = \frac<1 \cdot \sqrt<2>> <\sqrt<2>\cdot \sqrt<2>>= \frac<\sqrt<2>><2>\). Таким образом, получаем:

Значит в ответе вместо арксинусов нужно написать \(\frac<π><4>\).

Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac<7><6>\).

Решение:
И вновь тот, кто поторопился написать \( \left[ \beginx= \arcsin \frac<7><6>+2πn, n∈Z\\ x=π- \arcsin\frac<7><6>+2πl, l∈Z\end\right.\) на ЕГЭ потеряет \(2\) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать \(\arcsin⁡\frac<7><6>\)? Пролистайте до самого верха, туда, где было определение арксинуса. Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен \(1\) и больше или равен \(-1\). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.

Думаю, вы уловили закономерность.

Если \(\sin ⁡x\) равен не табличному значению между \(1\) и \(-1\), то решения будут выглядеть как: \( \left[ \beginx= \arcsin a +2πn, n∈Z\\ x=π- \arcsin a +2πl, l∈Z\end\right.\)

Арксинус отрицательного числа

Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:

Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:

Удивил последний пример? Почему в нем формула не работает? Потому что запись \(\arcsin⁡(-\frac<\sqrt<7>><2>)\) в принципе неверна, ведь \(-\frac<\sqrt<7>> <2>Синус
Тригонометрические уравнения