Урок «Арктангенс и арккотангенс. Решение уравнений tgx = а, ctgx = a»
Краткое описание документа:
Ранее по программе учащиеся получили представление о решении тригонометрических уравнений, ознакомились с понятиями арккосинуса и арксинуса, примерами решений уравнений cos t = a и sin t = a. В этом видеоуроке рассмотрим решение уравнений tg x = a и ctg x = a.
В начале изучения данной темы рассмотрим уравнения tg x = 3 и tg x = – 3. Если уравнение tg x = 3 будем решать с помощью графика, то увидим, что пересечение графиков функций y = tg x и y = 3 имеет бесконечное множество решений, где x = x1 + πk. Значение x1 – это координата x точки пересечения графиков функций y = tg x и y = 3. Автор вводит понятие арктангенса: arctg 3 это число, tg которого равен 3, и это число принадлежит интервалу от –π/2 до π/2. Используя понятие арктангенса, решение уравнения tg x = 3 можно записать в виде x = arctg 3 + πk.
По аналогии решается уравнение tg x = – 3. По построенным графикам функций y = tg x и y = – 3 видно, что точки пересечения графиков, а следовательно, и решениями уравнений, будет x = x2 + πk. С помощью арктангенса решение можно записать как x = arctg (– 3) + πk. На следующем рисунке увидим, что arctg (– 3) = – arctg 3.
Общее определение арктангенса выглядит следующим образом: арктангенсом а называется такое число из промежутка от –π/2 до π/2, тангенс которого равен а. Тогда решением уравнения tg x = a является x = arctg a + πk.
Автор приводит пример 1. Найти решение выражения arctg.Введем обозначения: арктангенс числа равен x, тогда tg x будет равен данному числу, где x принадлежит отрезку от –π/2 до π/2. Как в примерах в предыдущих темах, воспользуемся таблицей значений. По этой таблице тангенсу данного числа соответствует значение x = π/3. Запишем решение уравнения арктангенс заданного числа равен π/3, π/3 принадлежит и интервалу от –π/2 до π/2.
Пример 2 – вычислить арктангенс отрицательного числа. Используя равенство arctg (– a) = – arctg a, введем значение x. Аналогично примеру 2 запишем значение x, которое принадлежит отрезку от –π/2 до π/2. По таблице значений найдем, что x = π/3, следовательно, -– tg x = – π/3. Ответом уравнения будет – π/3.
Рассмотрим пример 3. Решим уравнение tg x = 1. Запишем, что x = arctg 1 + πk. В таблице значению tg 1 соответствует значение x = π/4, следовательно, arctg 1 = π/4. Подставим это значение в исходную формулу x и запишем ответ x = π/4 + πk.
Пример 4: вычислить tg x = – 4,1. В данном случае x = arctg (– 4,1) + πk. Т.к. найти значение arctg в данном случае нет возможности, ответ будет выглядеть как x = arctg (– 4,1) + πk.
Арктангенс, арккотангенс – свойства, графики, формулы
Арктангенс, arctg
Определение и обозначения
Арктангенс обозначается так:
.
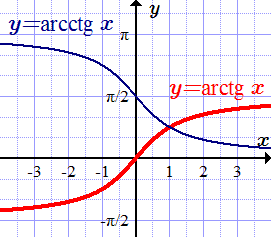
График функции арктангенс
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс, arcctg
Определение и обозначения
Арккотангенс обозначается так:
.
График функции арккотангенс
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(– x ) = arctg(–tg arctg x ) = arctg(tg(–arctg x )) = – arctg x
Функция арккотангенс не является четной или нечетной:
arcctg(– x ) = arcctg(–ctg arcctg x ) = arcctg(ctg(π–arcctg x )) = π – arcctg x ≠ ± arcctg x .
Свойства – экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x . (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | – ∞ | – ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/ 2 |
| – | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.
| x | arctg x | arcctg x | ||
| град. | рад. | град. | рад. | |
| – ∞ | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – 1 | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
Формулы
Формулы суммы и разности
при
при 0,\;xy > 1″ style=»width:122px;height:18px;vertical-align:-10px;background-position:-138px -570px»>
при 1″ style=»width:122px;height:18px;vertical-align:-10px;background-position:-261px -570px»>
при -1″ style=»width:76px;height:18px;vertical-align:-10px;background-position:-550px -570px»>
при 0,\;xy
при
Выражения через логарифм, комплексные числа
Выражения через гиперболические функции
Производные
Производные высших порядков:
Пусть . Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.
Аналогично для арккотангенса. Пусть . Тогда
;
.
Интегралы
Делаем подстановку x = tg t и интегрируем по частям:
;
;
;
Выразим арккотангенс через арктангенс:
.
Разложение в степенной ряд
При |x| ≤ 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс, соответственно.
Следующие формулы справедливы на всей области определения:
tg(arctg x ) = x
ctg(arcctg x ) = x .
Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg x ) = x при
arcctg(ctg x ) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов . Опубликовано: 14-07-2014 Изменено: 23-12-2018
Алгебра
План урока:
Арккосинус
Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:
Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1 1 либо а n ,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1) n окажется равным (– 1), и мы получим вторую серию.
Задание. Решите ур-ние
Задание. Запишите корни ур-ния
Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.
Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:
Ответ: 7π/3 и 8π/3.
Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние
Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:
Наконец, решениями ур-ния
Решение уравнений tgx = a и ctgx = a
Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):
Таким образом, у ур-ния tgx = a существует очевидное решение
Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:
Задание. Решите ур-ние
Задание. Запишите формулу корней ур-ния
Далее рассмотрим ур-ние вида
Задание. Решите ур-ние
Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии
Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.
http://1cov-edu.ru/mat_analiz/funktsii/obratnie_trigonometricheskie/arctg/
http://100urokov.ru/predmety/urok-4-prostejshaya-trigonometriya