Арктангенс и арккотангенс. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти арксинус и арккосинус от числа. Результат можно видеть как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Арктангенс и арккотангенс − теория, примеры и решения
Функция арктангенс и ее график
Функция тангенс определена в интервале [−∞;+∞] кроме точек 

 |
Однако, функцию тангенс можно разделить на интервалы, где она монотонна. Эти интервалы:
 , ,  , ,  , ,  и т.д. и т.д. |
По теореме об обратной функции, на каждом из указанных отрезков функция tg x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке 
| y=arctg x. | (1) |
Функция (1) − это функция, обратная к функции
 . . |
График функции арктангенс можно получить из графика функции 
 |
Свойства функции арктангенс.
- Область определения функции:
.
- Область значений функции:
.
- Функция является нечетной:
.
- Функция возрастает.
- Функция непрерывна.
Решим тригонометрическое уравнение
В интервале 
Следовательно в интервале 
 . . | (3) |
Решение уравнения (2) представлен на Рис.3:
 |
Так как tg t − это ординат точки пересечения прямой OMt1 c прямым x=1, то для любого a на линии тангенса есть только одна точка T(1; a). Прямая OTt пересекается с окружностью с радиусом 1 в двух точках: 



Пример 1. Решить тригонометрическое уравнение:
 . . |
Решение. Воспользуемся формулой (3):
 , , |
 . . |
Пример 2. Решить тригонометрическое уравнение:
 . . |
Решение. Воспользуемся формулой (3):
 . . |
Используя онлайн калькулятор получим:
 . . |
Функция арккотангенс и ее график
Как известно, функция котангенс определена в интервале [−∞;+∞] кроме точек -2π, —π 0, π, 2π. и не является монотонной функцией (Рис.4) (подробнее о функции котангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.
 |
Однако, функцию кокотангенс можно разделить на интервалы, где она монотонна. Эти интервалы:
  |
По теореме об обратной функции, на каждом из указанных интервалов функция ctg x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке 
| y=arcctg x. | (4) |
Функция (4) − это функция, обратная к функции
 . . |
График функции арккотангенс можно получить из графика функции 
 |
Свойства функции арккотангенс.
- Область определения функции:
.
- Область значений функции:
.
- Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
- Функция убывает.
- Функция непрерывна.
Решим тригонометрическое уравнение
В интервале (0; π) для уравнения (5) существует одно t, для которого сtg t=a. Это t=arcctg a. Следовательно в интервале (0; π) уравнение (5) имеет один корень. Так как котангенс периодичная функция с основным периодом π, то общее решение уравнения (5) имеет следующий вид:
 | (6) |
Решения уравнения (5) можно представить на единичной окружности (Рис.6):
 |
ctg t − это абсцис точки пересечения прямой 





Пример 1. Решить тригонометрическое уравнение:
 . . |
Решение. Воcпользуемся формулой (6):
 . . |
Так как в интервале (0; π)
 . . |
Пример 2. Решить следующее тригонометрическое уравнение:
 . . |
Решение. Используя формулу (6), имеем
 . . |
С помощью онлайн калькулятора вычисляем 
Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом
Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg
Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.
Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса
Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.
д л я α ∈ — 1 , 1 sin ( a r c c i s α ) = α , cos ( a r c cos α ) = α , д л я α ∈ ( — ∞ , ∞ ) t g ( a r c t g α ) = α , c t g ( a r c c t g α ) = α
Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.
Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса
д л я — π 2 ≤ α ≤ π 2 a r c sin ( sin α ) = α , д л я 0 ≤ α ≤ π arccos ( cos α ) = α , д л я — π 2 α π 2 arctg ( tg α ) = α , д л я 0 α π arcctg ( ctg α ) = α
Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.
Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел
В этом блоке мы сформулируем важное утверждение:
Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.
д л я α ∈ — 1 , 1 a r c c i s ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , д л я α ∈ ( — ∞ , ∞ ) a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — arcctg α
Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.
Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс
Они выглядят следующим образом:
д л я α ∈ — 1 , 1 a r c c i s α + a r c cos α = π 2 , д л я α ∈ ( — ∞ , ∞ ) a r c t g α + a r c c t g α = π 2
Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.
| — 1 ≤ α ≤ 1 , sin ( a r c sin α ) = α | — 1 ≤ α ≤ 1 , sin ( a r c cos α ) = 1 — α 2 | — ∞ ≤ α ≤ + ∞ , sin ( a r c t g α ) = α 1 + α 2 | — ∞ ≤ α ≤ + ∞ , sin ( a r c c t g α ) = 1 1 + α 2 |
| — 1 ≤ α ≤ 1 , cos ( a r c sin α ) = 1 — α 2 | — 1 ≤ α ≤ 1 , cos ( a r c cos α ) = α | — ∞ ≤ α ≤ + ∞ , cos ( a r c t g α ) = 1 1 + α 2 | — ∞ ≤ α ≤ + ∞ , cos ( a r c c t g α ) = 1 1 + α 2 |
| — 1 α 1 , t g ( a r c sin α ) = α 1 — α 2 | α ∈ ( — 1 , 0 ) ∪ ( 0 , 1 ) , t g ( a r c cos α ) = 1 — α 2 α | — ∞ ≤ α ≤ + ∞ , t g ( a r c t g α ) = α | α ≠ 0 , t g ( a r c c t g α ) = 1 α |
| α ∈ ( — 1 , 0 ) ∪ ( 0 , 1 ) , c t g ( a r c sin α ) = 1 — α 2 α | — 1 α 1 , c t g ( a r c cos α ) = α 1 — α 2 | α ≠ 0 , c t g ( a r c t g α ) = 1 α | — ∞ ≤ α ≤ + ∞ , c t g ( a r c c t g α ) = α |
Теперь разберем примеры, как они применяются в задачах.
Вычислите косинус арктангенса из 5 .
Решение
У нас для этого есть подходящая формула следующего вида: cos ( a r c t g α ) = 1 1 + α 2
Подставляем нужное значение: cos ( a r c t g 5 ) = 1 1 + ( 5 ) 2 = 2 6
Вычислить синус арккосинуса 1 2 .
Решение
Для этого нам понадобится формула: sin ( a r c cos α ) = 1 — a 2
Подставляем в нее значения и получаем: sin ( a r c cos 1 2 ) = 1 — ( 1 2 ) 2 = 3 2
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin ( a r c cos 1 2 ) = sin π 3 = 3 2
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
Для того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций — косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:
sin 2 α + cos 2 α = 1 1 + c t g 2 α = 1 sin 2 α
Вспомним, что t g α · c t g α = 1 . Из этого можно получить:
sin α = 1 — cos 2 α , 0 ≤ α ≤ π sin α = t g α 1 + t g 2 α , — π 2 α π 2 sin α = 1 1 + c t g 2 α , 0 α π
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Теперь в первой формуле вместо a мы добавим arccos a. Итог — формула синуса арккосинуса.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
- sin α = 1 — cos 2 α , 0 ≤ α ≤ π
Следовательно, sin ( a r c cos α ) = 1 — cos 2 ( a r c cos α ) = 1 — a 2
- sin α = t g α 1 + t g α , — π 2 α π 2 ,
Следовательно, sin ( a r c t g α ) = t g ( a r c t g α ) 1 + t g 2 ( a r c t g α ) = α 1 + α 2
- sin α = 1 1 + c t g 2 α , 0 α π
Следовательно, sin ( a r c t g α ) = 1 1 + t g 2 ( a r c t g α ) = 1 1 + α 2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
- Из cos α = 1 — sin 2 α , — π 2 ≤ α ≤ π 2 следует, что
cos ( a r c sin α ) = 1 — sin 2 ( a r c sin α ) = 1 — a 2
- Из cos α = 1 1 + t g 2 α , — π 2 α π 2 следует, что
- Из cos α = c t g α 1 + c t g 2 α , 0 α π cos ( a r c t g α ) = 1 1 + t g 2 ( a r c t g α ) = 1 1 + α 2
следует, что cos ( a r c t g α ) = c t g ( a r c c t g α ) 1 + c t g 2 ( a r c c t g α ) = α 1 + α 2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
- Исходим из t g α = sin α 1 — sin 2 α , — π 2 α π 2 . Получаем t g ( a r c sin α ) = sin ( a r c sin α ) 1 — sin 2 ( a r c sin α ) = α 1 — α 2 при условии, что — 1 α 1 .
- Исходим из t g α = 1 — cos 2 α cos α , α ∈ [ 0 , π 2 ) ∪ ( π 2 , π ] , получаем
t g ( a r c cos α ) = 1 — cos 2 ( a r c cos α ) cos ( a r c c os α ) = 1 — α 2 α при условии α ∈ ( — 1 , 0 ) ∪ ( 0 , 1 ) .
- Исходим из t g α = 1 c t g α , α ∈ ( 0 , π 2 ) ∪ ( π 2 , π ) , получаем t g ( a r c c t g α ) = 1 c t g ( a r c c t g α ) = 1 α при условии, что α ≠ 0 .
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
c t g α = 1 t g α
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
a r c sin α = a r c cos 1 — α 2 , 0 ≤ α ≤ 1 — a r c cos 1 — a 2 , — 1 ≤ α 0 a r c sin α = a r c t g α 1 — α 2 , — 1 α 1 a r c sin α = a r c c t g 1 — α 2 α , 0 α ≤ 1 a r c c t g 1 — α 2 α — π , — 1 ≤ α ≤ 0
А так мы выразим арккосинус через остальные обратные функции:
a r c cos α = a r c sin 1 — α 2 , 0 ≤ α ≤ 1 π — arcsin 1 — α 2 , — 1 ≤ α 0 a r c cos α = a r c t g 1 — α 2 α , 0 α ≤ 1 π + arctg 1 — α 2 α , — 1 α 0 arccosα = arcctg α 1 — α 2 , — 1 α 1
Формула выражения арктангенса:
a r c t g α = a r c sin α 1 + α 2 , — ∞ α + ∞ a r c t g α = a r c cos 1 1 + α 2 , α ≥ 0 — a r c cos 1 1 + α 2 , α 0 a r c t g α = a r c c t g 1 α , α ≠ 0
Последняя часть – выражение арккотангенса через другие обратные функции:
a r c c t g α = a r c sin 1 1 + α 2 , α ≥ 0 π — a r c sin 1 1 + α 2 , α 0 a r c c t g α = a r c cos α 1 + α 2 , — ∞ α + ∞ a r c c t g α = a r c t g 1 α , α ≠ 0
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Возьмём a r c sin α = a r c t g α 1 — α 2 , — 1 α 1 и постараемся вывести доказательство.
Мы знаем, что a r c t g α 1 — α 2 — это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:
sin ( a r c t g α 1 — α 2 ) = α 1 — α 2 1 + ( α 1 — α 2 ) 2 = α 1 — α 2 1 + α 2 1 — α 2 = α 1 — α 2 1 + α 2 1 — α 2 = α 1 — α 2 1 1 — α 2 = α
Получается, что a r c t g α 1 — α 2 при условии 1 a 1 – это и есть арксинус числа a .
Вывод: a r c sin a = a r c t g a 1 — a 2 , — 1 a 1
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Условие Вычислить синус арккотангенса минус корня из 3 .
Решение
Нам понадобится формула выражения арккотангенса через арксинус: a r c c t g α = a r c sin 1 1 + a 2 , α ≥ 0 π — arcsin 1 1 + a 2 , α 0
Подставим в нее α = — 3 и получим ответ – 1 2 . Непосредственное вычисление дало бы нам те же результаты: sin ( a r c c t g ( — 3 ) ) = sin 5 π 6 = 1 2 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sin α = 1 1 + c t g 2 α , 0 α π
В итоге у нас бы вышло: sin ( a r c c t g ( — 3 ) ) = 1 1 + c t g 2 ( a r c c t g ( — 3 ) ) = 1 1 + ( — 3 ) 2 = 1 2
Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin ( a r c c t g α ) = 1 1 + α 2 sin ( a r c c t g ( — 3 ) ) = 1 1 + ( — 3 ) 2 = 1 2
Прочие формулы с обратными функциями
Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:
sin 2 α 2 = 1 — cos α 2
Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:
sin α 2 = 1 — cos α 2
Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:
sin a r c cos α 2 = 1 — cos ( a r c cos α ) 2 ⇔ sin a r c cos α 2 = 1 — α 2
Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:
a r c cos α 2 = a r c sin 1 — α 2
Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.
В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
Арктангенс, арккотангенс – свойства, графики, формулы
Арктангенс, arctg
Определение и обозначения
Арктангенс обозначается так:
.
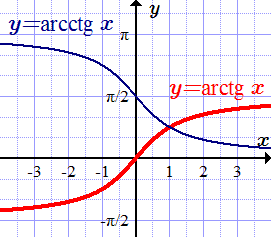
График функции арктангенс
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс, arcctg
Определение и обозначения
Арккотангенс обозначается так:
.
График функции арккотангенс
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(– x ) = arctg(–tg arctg x ) = arctg(tg(–arctg x )) = – arctg x
Функция арккотангенс не является четной или нечетной:
arcctg(– x ) = arcctg(–ctg arcctg x ) = arcctg(ctg(π–arcctg x )) = π – arcctg x ≠ ± arcctg x .
Свойства – экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x . (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | – ∞ | – ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/ 2 |
| – | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.
| x | arctg x | arcctg x | ||
| град. | рад. | град. | рад. | |
| – ∞ | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – 1 | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
Формулы
Формулы суммы и разности
при
при 0,\;xy > 1″ style=»width:122px;height:18px;vertical-align:-10px;background-position:-138px -570px»>
при 1″ style=»width:122px;height:18px;vertical-align:-10px;background-position:-261px -570px»>
при -1″ style=»width:76px;height:18px;vertical-align:-10px;background-position:-550px -570px»>
при 0,\;xy
при
Выражения через логарифм, комплексные числа
Выражения через гиперболические функции
Производные
Производные высших порядков:
Пусть . Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.
Аналогично для арккотангенса. Пусть . Тогда
;
.
Интегралы
Делаем подстановку x = tg t и интегрируем по частям:
;
;
;
Выразим арккотангенс через арктангенс:
.
Разложение в степенной ряд
При |x| ≤ 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс, соответственно.
Следующие формулы справедливы на всей области определения:
tg(arctg x ) = x
ctg(arcctg x ) = x .
Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg x ) = x при
arcctg(ctg x ) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов . Опубликовано: 14-07-2014 Изменено: 23-12-2018
http://zaochnik.com/spravochnik/matematika/trigonometrija/osnovnye-formuly-s-arksinusom-arkkosinusom-arktang/
http://1cov-edu.ru/mat_analiz/funktsii/obratnie_trigonometricheskie/arctg/

 .
. .
. .
. .
.