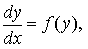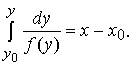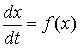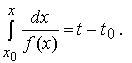Автономная система дифференциальных уравнений первого порядка

Автономная система дифференциальных уравнений первого порядка

Автономным уравнением первого порядка называется уравнение вида

правая часть f ( y ) которого не зависит от x .

Решение y ( x ) ≡ 0 называется неподвижной точкой уравнения.

Для автономного уравнения решение задачи Коши 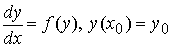определяется равенством:

Например, дифференциальное уравнение

описывает движение материальной точки по оси x под действием внешних сил f ( x ) . Координата точки x ( t ) в момент времени t — решение дифференциального уравнения . Скорость движения точки задана функцией f ( x ) . В момент времени t координата x ( t ) точки, которая в начальный момент t ₀ имела координату x ₀, определяется равенством

При t → ∞ функция x ( t ) может быть ограниченной, может стремиться к конечному пределу, может ”уходить на бесконечность” ( x ( t ) → ∞) или может быть неограниченной с каким-то более сложным поведением.

Автономная система дифференциальных уравнений первого порядка

Система обыкновенных дифференциальных уравнений называется автономной, если независимая переменная не входит явно в систему.

Рассмотрим автономные системы второго порядка:

Будем полагать, что правые части системы f₁(x₁, x₂), f₂(x₁, x₂) непрерывно дифференцируемы в области определения, т.е. справедлива теорема существования и единственности.
Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx₁/dt и dx₂/dt зависят только от x₁ и x₂. Автономные системы называют также динамическими системами.

Пусть x₁= j ₁(t), x₂= j ₂(t) — решение автономной системы второго порядка. Тогда уравнения

задают в параметрической форме кривую на плоскости (x₁, x₂). Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы. Именно поэтому автономные системы второго порядка принято называть автономными системами на плоскости.

Для фазовых траекторий автономной системы с непрерывно дифференцируемой правой частью справедливы следующие утверждения:

• две фазовые кривые либо не имеют общих точек, либо совпадают;
• фазовая траектория, отличная от точки, есть гладкая кривая (в каждой ее точке есть ненулевой касательный вектор);
• всякая фазовая кривая принадлежит к одному из трех типов— гладкая кривая без самопересечений, замкнутая гладкая кривая (цикл), точка.

ПРИМЕР 1. Виды фазовых кривых.

Если фазовая траектория x₁= j₁(t), x₂= j₂(t) — замкнутая гладкая кривая g, в некоторой окрестности которой нет других замкнутых траекторий, то она является предельным циклом: все траектории, которые начинаются достаточно близко от g, спиралевидно приближаются к ней либо при , либо при .
Предельные циклы бывают трех типов:

• устойчивые — близкие траектории «навиваются» на него при (пример 2);
• неустойчивые— близкие траектории уходят от него при (пример 3);
• полуустойчивые — траектории, лежащие по одну сторону от цикла, «навиваются» на него при , а лежащие по другую строну — «отходят» от цикла (пример 4).

ПРИМЕР 2. Устойчивый предельный цикл.

ПРИМЕР 3. Неустойчивый предельный цикл.

ПРИМЕР 4. Полуустойчивый предельный цикл.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter