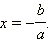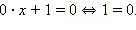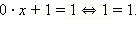Ax b 0 найти корень уравнения

Ax b 0 найти корень уравнения

Уравнение вида , где − переменная, − некоторые действительные числа, называется уравнением степени не выше первой .

Если , то решением уравнения является любое число.

Если и , то уравнение корней не имеет.

Если , то уравнение называется линейным и имеет ровно одно решение

Корнем этого уравнения является число 1, поскольку при подстановке вместо этого числа получается верное числовое равенство.

Решите уравнение 0 ∙ + 1 = 0.

Имеем:

Это уравнение не имеет решений, поскольку ни при каких значениях переменной (которая, очевидно, явно не входит в уравнение) равенство не имеет место.

Ответ. Нет решений.

Решите уравнение 0 ∙ + 1 = 1.

Имеем

Решением этого уравнения является любое действительное число. В самом деле, при любом значении переменной равенство является верным.

Квадратное уравнение

Квадратное уравнение — это уравнение вида ax² + bx + c, где a, b, c — некоторые числа (причём обязательно a ≠ 0),

В таком уравнении:

• x — переменная, которая присутствует в таком уравнении во второй степени,
• a — первый коэффициент,
• b — второй коэффициент,
• c — свободный член.

Ещё такое уравнение называется квадратный трёхчлен, т.к. самая большая степень в нём квадрат и он состоит из 3 одночленов.

Для решения таких уравнений сначала находится дискриминант по этой формуле:

• D корней не существует,
• D = 0 есть один корень,
• D > 0 есть два корня.

Пример: x² – x – 3 = 0; a = 1, b = –1, c = –3, D = (–1)² – 4×1×(–3) = 1 + 12 = 13, D > 0 есть два корня.

Когда уже точно известно, что корни существуют, и известно количество этих корней, можно приступить к их поиску с помощью этой формулы:

Пример: x² – x – 3 = 0; a = 1, b = –1, c = –3, D = 13.

x1 = (1 + √13)/2 ≈ (1 + 3,60555)/2 ≈ 2,302775

x2 = (1 – √13)/2 ≈ (1 – 3,60555)/2 ≈ -1,302775

Примеры

Пример 1

20x² – 15x – 10 = 0

Лучше сразу выписать так: a = 20, b = – 15, c = – 10.

1. Ищем дискриминант: формула D = b² – 4ac D = (– 15)² – 4 × 20 × (– 10) = 225 + 800 = 1025; D > 0 значит есть два корня.

2. Ищем эти корни: формула корней

2.1. Разбиваем формулу на две части, первый корень:

Уравнение 20x² – 15x – 10 = 0, где a = 20, b = – 15, c = – 10; D =1025.

x1 = ((–(–15)) + √ 1025)/(2×20) = (15 + 32,0156) / 40 ≈ 1,17539

2.2. Второй корень:

Уравнение 20x² – 15x – 10 = 0, где a = 20, b = – 15, c = – 10; D =1025.

x2 = ((–(–15)) – √ 1025)/(2×20) ≈ (15 – 32,0156) / 40 ≈ -0,42539

Пример 2

a = –1, b = 6, c = 18

Дискриминант D = b² – 4ac

D = 6² – 4×(–1)×(18) = 36 + 72 = 108, D > 0 есть два корня

a = –1, b = 6, c = 18, D = 108

x1 = ((–6) +√108)/(–2) = ((–6) + 10,3923)/(–2) = – 2,19615

x2 = ((–6) –√108)/(–2) = ((–6) – 10,3923)/(–2) = 8,19615

Как разложить квадратный трёхчлен на множители?

Продолжим с примером уравнения 20x² – 15x – 10 = 0

Мы уже нашли корни

x1 ≈ 1,17539, x2 ≈ -0,42539

Выносим коэффициент x² за скобки, и оба корня ставятся с противоположными знаками таким образом:

20x² – 15x – 10 = 20 (x – 1,17539) (x+0,42539)

Хотите проверить? Открываем скобки и проверяем

20 (x – 1,17539) (x+0,42539) = 20 (x²–1,17539x + 0,42539x–0,42539×1,17539) = 20 (x²–0,75x – 0,4999991521) =

Погрешность в 0,000016958 должна быть из-за округления в предыдущих расчётах.

Виды квадратных уравнений

Полное и неполное квадратное уравнение

В полном уравнении присутствуют все три его члена (ax² + bx + c = 0). В противном случае уравнение неполное, например:

–x² – 9 = 0 (отсутствует bx)

x² + 16x = 0 (отсутствует с)

–5x² = 0 (отсутствуют bx и с)

Т.е. это когда коэффициент с = 0 или b = 0 (или оба одновременно равны нулю). Внимание: о том, что «a» может быть равно нулю, не говорится, т.к. таким образом уравнение станет линейным (ax + b = 0).

Как решать неполное квадратное уравнение?

Способ решения, когда b=0

5x² = 5, делим всё на 5

x = ± √1 ⇔ x = 1 или x = –1

Первый способ решения, когда c=0 (это быстрый метод)

x² + 16x = 0 (выносим x за скобки)

x (x + 16) = 0, таким образом, либо x = 0, либо то, что в скобках, равно нулю,

x = 0 или (x + 16)= 0

(x + 16)= 0 ⇔ x = – 16

Второй способ решения, когда c=0

Неполное уравнение (c=0, b=0 или когда оба равны нулю) можно решить по той же системе, как и полное, правильно выписав коэффициенты (но это долго и нерационально).

a = 1, b = 16, c = 0 (здесь отсутствует c, значит он равен нулю)

Дискриминант: D = b² – 4ac = 16² – 4×1×0 = 16² = 256 >0, есть два корня.

Ищем корни X1,2 = ((–b) ±√D)/(2×(a)) =>

x1 = ((–16) + √256)/(2×(1)) = ((–16) + 16)/2 = 0

x2 = ((–16) – √256)/(2×(1)) = ((–16) – 16)/2 = –32/2 = – 16

Способ решения, когда b=0 и c=0

Приведённое квадратное уравнение

Чтобы получить приведённое квадратное уравнение, нужно лишь разделить обе части уравнения на a:

x² + px + q = 0, где:

3x² – 6x = 0 (делим всё на 3) ⇔ x² – (6/3)x = 0 ⇔ x² – 2x = 0 (неполное приведённое)

2x² – 4x – 2 = 0 (делим всё на 2) ⇔ x² – (4/2)x – (2/2) = 0 ⇔ x² – 2x – 1 = 0 (полное приведённое)

Геометрический смысл решения корней квадратных уравнений

Корни квадратного уравнения ещё являются и нулями функции, т.е. если вы ищете нули функции (в каких точках функция пересекает ось Ox), то вы их найдёте именно через этот процесс: поймёте, если они существуют, рассчитав дискриминант, затем найдёте их, используя формулу корней.

Вспомним наш пример уравнения 20x² – 15x – 10 = 0.

Узнайте также, что такое Теорема Виета и Парабола.

Линейные уравнения

Линейные уравнения – уравнения, которые можно представить в виде \(ax+b=0\), где \(a\) и \(b\) – какие-либо числа.

Проще говоря, это такие уравнения , в которых переменные (обычно иксы) в первой степени . При этом не должно быть переменных в знаменателях дробей .

А тут \(a=0, b=5\) (пояснение: данное уравнение может быть представлено в виде \(0\cdot x+5=0\))

Здесь \(a\) и \(b\) изначально не определены, но преобразовав уравнение, мы сможем их найти.

Тоже самое, \(a\) и \(b\) пока что неизвестны.

Решение линейных уравнений

При решении линейных уравнений, мы стремимся найти корень, то есть такое значение для переменной, которое превратит уравнение в правильное равенство.

В простых уравнениях корень очевиден сразу или легко находиться подбором. Например, понятно, что корнем уравнения \(x+3=5\) будет число \(2\), ведь именно двойка при подстановке ее вместо икса даст \(5=5\) – верное равенство.

Однако в более сложных случаях ответ сразу не виден. И тогда на помощь приходят равносильные преобразования .

Чтобы найти корень уравнения нужно равносильными преобразования привести данное нам уравнение к виду

Это число и будет корнем.

То есть, мы преобразовываем уравнение, делая его с каждым шагом все проще, до тех пор, пока не сведем к совсем примитивному уравнению «икс = число», где корень – очевиден. Наиболее часто применяемыми при решении линейных уравнений являются следующие преобразования:

1. Прибавление или вычитание из обеих частей уравнения одинакового числа или выражения.

Например: прибавим \(5\) к обеим частям уравнения \(6x-5=1\)

Обратите внимание, что тот же результат мы могли бы получить быстрее – просто записав пятерку с другой стороны уравнения и поменяв при этом ее знак. Собственно, именно так и делается школьный «перенос через равно со сменой знака на противоположный».

2. Умножение или деление обеих частей уравнения на одинаковое число или выражение.

Например: разделим уравнение \(-2x=8\) на минус два

Обычно данный шаг выполняется в самом конце, когда уравнение уже приведено к виду \(ax=b\), и мы делим на \(a\), чтобы убрать его слева.

3. Использование свойств и законов математики: раскрытие скобок, приведение подобных слагаемых, сокращение дробей и т.д.

Чаще всего при решении линейного уравнения приходиться делать несколько разных преобразований.

Пример. Решить линейное уравнение \(6(4-x)+x=3-2x\)

Прибавляем \(2x\) слева и справа

Вычитаем \(24\) из обеих частей уравнения

Опять приводим подобные слагаемые

Теперь делим уравнение на \(-3\), тем самым убирая коэффициент перед иксом в левой части.

Ответ найден. Однако давайте его проверим. Если семерка действительно корень, то при подстановке ее вместо икса в первоначальное уравнение должно получиться верное равенство — одинаковые числа слева и справа. Пробуем.

Сошлось. Значит, семерка и в самом деле является корнем исходного линейного уравнения.

Не ленитесь проверять подстановкой найденные вами ответы, особенно если вы решаете уравнение на контрольной или экзамене.

Остается вопрос – а как определить, что делать с уравнением на очередном шаге? Как именно его преобразовывать? Делить на что-то? Или вычитать? И что конкретно вычитать? На что делить?

Ваша цель – привести уравнение к виду \(x=[число]\), то есть, слева икс без коэффициентов и чисел, а справа – только число без переменных. Поэтому смотрите, что вам мешает и делайте действие, обратное тому, что делает мешающий компонент.

Чтобы лучше это понять, разберем по шагам решение линейного уравнения \(x+3=13-4x\).

Давайте подумаем: чем данное уравнение отличается от \(x=[число]\)? Что нам мешает? Что не так?

Ну, во-первых, мешает тройка, так как слева должен быть только одинокий икс, без чисел. А что «делает» тройка? Прибавляется к иксу. Значит, чтобы ее убрать — вычтем такую же тройку. Но если мы вычитаем тройку слева, то должны вычесть ее и справа, чтобы равенство не было нарушено.

Хорошо. Теперь что мешает? \(4x\) справа, ведь там должны быть только числа. \(4x\) вычитается — убираем прибавлением.

Теперь приводим подобные слагаемые слева и справа.

Уже почти готово. Осталось убрать пятерку слева. Что она «делает»? Умножается на икс. Поэтому убираем ее делением.

Решение завершено, корень уравнения – двойка. Можете проверить подстановкой.

Заметим, что чаще всего корень в линейных уравнениях только один. Однако могут встретиться два особых случая.