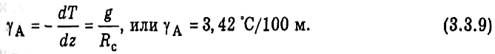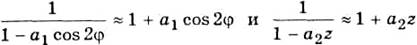Барометрическое уравнение для изотермической атмосферы

Барометрические формулы

Уравнение статики является одним из важнейших уравнений метеорологии, на основе которого устанавливаются закономерности распределения давления, плотности и массы воздуха по высоте. В своем дифференциальном виде уравнение статики (3.2.4) позволяет выполнить расчет изменения давления лишь для малых прираще­ний высоты dz.

На практике всегда необходимо иметь данные о распределении давления в слоях атмосферы конечной толщины или определить толщину таких слоев по измеренным значениям давления. Для этой цели уравнение статики следует записать в конечном (интеграль­ном) виде, т. е. найти его интегралы. Интегралы уравнения статики атмосферы, полученные при разных предположениях относительно изменения температуры и плотности воздуха с высотой, носят об­щее название барометрических формул. На основе барометриче­ских формул решаются такие важные практические задачи, как расчет распределения давления и плотности по высоте, определение высоты различных летательных аппаратов по измеренному давле­нию, приведение давления к уровню моря и др.

Для получения интегральной формы уравнения статики проин­тегрируем левую и правую части (3.2.4) в пределах от уровня моря 2=0 (или земной поверхности), где давление р0, до произвольной высоты г, где давление р. Имеем

Здесь ρ = ρ(z) – функция высоты

Другую интегральную форму уравнению статики можно при­дать, если воспользоваться уравнением состояния влажного воздуха (1.4.12) из главы 1. Подставив найденное отсюда значение р, пере­пишем (3.2.4) в виде

.

Интегрируя в пределах от 0 до z и от р₀ до р, получаем:

Интегральные формы (3.3.1) и (3.3.3) уравнения статики в даль­нейшем широко используются для получения различных баромет­рических формул. Заметим, что p₀ в формулах (3.3.1) и (3.3.3) может обозначать давление как на уровне моря, так и на поверхности Земли. Различие будет состоять лишь в начале отсчета высоты г. В общем случае температура, а вместе с ней и плотность воздуха явля­ются достаточно сложными функциями высоты, установить анали­тический вид которых не всегда представляется возможным. Поэто­му прежде чем перейти к общему случаю, рассмотрим несколько ча­стных случаев, отличающихся один от другого различными предпо­ложениями относительно вида функций Т = T(z) или р = р(z), с по­мощью которых описывается распределение температуры или плот­ности по высоте.

Однородная атмосфера. Предположим, что плотность воздуха в пределах всей атмосферы

не изменяется с высотой, т. е.

Здесь р₀— плотность воздуха при z = 0. Такая атмосфера носит на­звание однородной. Пренебрежем зависимостью ускорения свобод­ного падения от высоты. Тогда на основании (3.3.1) получаем баро­метрическую формулу однородной атмосферы:

Согласно этой формуле, давление в однородной атмосфере убывает с высотой по линейному закону (рис. 3.2).

Отметим, что в приложении к атмо­сфере формула (3.3.5) дает заведомо дале­кое от реальных условий распределение давления. Однако для гидросферы, плот­ность которой изменяется в очень узких пределах (плотность воды близка к 1 г/см3), формула (3.3.5) дает вполне удовлетворительные результаты. Поэтому ее можно назвать барометрической фор­мулой гидросферы (высота в этом случае отсчитывается от дна моря или океана).

Поставим вопрос о высоте однородной атмосферы, т. е. такой высоте, на которой давление обращается в нуль (р = 0).

Обо­значим ее через Н. Согласно (3.3.5), имеем

Поскольку в соответствии с уравнением (1.3.8) р₀/ρ₀ = R_cT₀ (T₀— температура воздуха при z = 0), формула (3.3.6) принимает вид

Отсюда следует, что высота однородной атмосферы конечна и зави­сит только от

температуры воздуха на поверхности Земли. При Т = О °С она составляет

Поскольку плотность в однородной атмосфере постоянна, а дав­ление быстро убывает с высотой, температура ее, равная в соответ­ствии с уравнением состояния

должна понижаться. Если взять производную по высоте от левой и правой части (3.3.8), то получим:

Привлекая (3.2.5), находим следующее выражение для верти­кального градиента температуры

у_А в однородной атмосфере:

Таким образом, в однородной атмосфере температура убывает с высотой по линейному закону:

при этом скорость понижения температуры (градиент) значительно больше среднего значения у в пределах тропосферы.

Изменение плотности воздуха с высотой. Рассмотрим вопрос об изменении плотности воздуха с высотой в общем случае. С этой целью сначала прологарифмируем, а затем продифференцируем по высоте левую и правую часть уравнения состояния (1.3.8):

Заменив dp/dz в соответствии с (3.2.5) и подставив в полученное выражение р из уравнения (1.3.8), найдем:

Формула (3.3.11) справедлива для любого распределения темпе­ратуры воздуха по высоте. На основе ее можно сделать выводы отно­сительно изменения плотности воздуха с высотой. Возможны три различных случая.

1. Если γ > γ_А= 3,42 o С/100 м, то dρ/dz > 0, т. е. плотность возду­ха возрастает с высотой. Вертикальные градиенты температуры γ, превышающие 3,42 o С/100 м, в реальных условиях атмосферы мо­гут наблюдаться лишь в дневные часы (летом) в приземном слое ат­мосферы. При таких условиях плотность в этом слое увеличиваетсяс высотой.

2. Если γ = γ_А, то dρ/dz = 0, т. е. плотность воздуха не изменяет­ся с высотой (постоянна): ρ = ρ₀ = const. Это случай однородной ат­мосферы.

3. Если γ γ_А. Таким образом, наиболее характерным состоянием атмосферы является такое, ког­да плотность воздуха убывает с высотой.

Изотермическая атмосфера. Атмосфера называется изотерми­ческой, если температура не изменяется с высотой, т. е.

Т = То = const,

где То — температура на уровне моря или поверхности Земли. Изо­термическая атмосфера по своим свойствам во многом противопо­ложна однородной атмосфере. Считая атмосферу сухой и пренебре­гая зависимостью ускорения свободного падения от высоты, на основании (3.3.3) и последнего соотношения получаем барометриче­скую формулу изотермической атмосферы:

Давление в изотермической атмосфере убывает с высотой по экс­поненциальному (показательному) закону

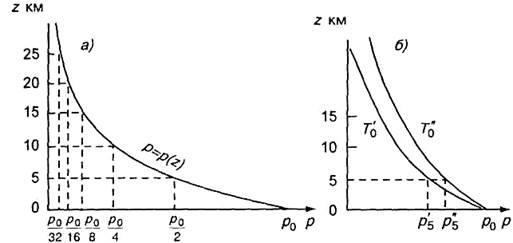
Графически зависимость давления р от высоты z в изотермиче­ской атмосфере представлена на рис. 3.3. Рисунок 3.3 а поясняет вытекающую из формулы (3.3.12) закономерность: если высота воз­растает в прогрессии арифметической, то давление убывает в про­грессии геометрической. Кривые на рис. 3.3 б соответствуют раз­личным температурам атмосферы (постоянным по высоте): T ′′ ₀ > T ′ ₀. Из этого рисунка и анализа формулы (3.3.12) следует, что при од­ном и том же давлении у земной поверхности давление на высотах (например 5, 10, 15 км) при температуре T ′′ ₀ больше, чем при T ′ ₀. Одно и то же значение давления наблюдается при температуре T ′′ ₀ на более высоких уровнях, чем при температуре T ′ ₀. Это означает, что при более высокой температуре давление в изотермической атмо­сфере убывает с высотой медленнее, чем при более низкой темпе­ратуре.

Абсолютное значение убывания давления в слоях равной толщи­ны в нижней части атмосферы больше, чем в верхней. Так, в слое от О до 5 км давление при средних условиях падает на p₀ — p₀/2 = p₀/2, т. е. примерно на 500 гПа (при р₀ = 1000 гПа); в слое от 5 до 10 км падение давления составляет р₀/2 — р₀/4 = р₀/4 т. е. около 250 гПа, а в слое от 20 до 25 км давление уменьшается всего лишь на р₀/16 — р₀/32 = р₀/32, т. е. примерно на 31—32 гПа. Таким образом, чем выше расположен слой атмосферы определен­ной толщины, тем меньше падение давления в этом слое.

Рис. 3.3. Распределение давления по высоте в изотермической атмосфере.

а — общая закономерность падения давления, б — падение давления при разных темпе­ратурах (T ′′ ₀ > T ′ ₀).

Высота изотермической атмосферы равна бесконечности, т. е. р → 0 только при z → ∞.

Формула для плотности воздуха может быть получена, если обратиться к уравнению состояния, согласно которому

Поскольку в изотермической атмосфере Т/Т₀ =1, то на основа­нии (3.3.12) получаем

Величина δ = ρ/ρо носит название относительной плотности.

Политропная атмосфера. Политропной называют такую атмо­сферу, которая характеризуется линейным изменением температу­ры с высотой (или постоянным значением вертикального градиента температуры):

Считая атмосферу сухой (T_υ = Т) и подставляя Т в соответствии с (3.3.14) в формулу (3.3.3), получаем:

Выполнив интегрирование (в предположении g — const), прихо­дим к барометрической формуле политропной атмосферы:

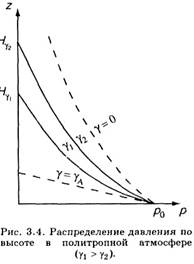
Графически зависимость р от z изображена на рис. 3.4. Кривые соответствуют одним и тем же значениям р₀ и T₀, но различным значениям вертикального градиента температуры: γ₁ и γ₂. Давле­ние при большем значении вертикального градиента температуры (γ₁) убывает с высотой быстрее, чем при меньшем (γ₂). Для сравне­ния на рис. 3.4 приведены кривые изменения давления в однород­ной и изотермической атмосферах (штриховые кривые). Высота по­литропной атмосферы конечна. В самом деле, согласно (3.3.15), дав­ление обращается в нуль на такой высоте z = Н_γ, на которой

Высота политропной атмосферы изменяется в широких пределах; при Т₀ = 288 К и γ = 0,65 К/100 м значе­ние Нγ составляет 44,3 км.

Формула для плотности воздуха в политропной атмосфере имеет вид

Полная барометрическая форму­ла (формула Лапласа).

Рассмотрим общий случай, т. е. случай произ­вольного распределения температуры по высоте. Учтем также, что реаль­ный воздух влажный, а ускорение свободного падения — функция ши­роты и высоты. Привлекая соотноше­ние (3.1.2) и учитывая, что

уравнение (3.3.2) перепишем в виде

(вследствие малости слагаемых а₁ cos 2φ> и a₂z по сравнению с едини­цей), то формулу (3.3.18) приведем к виду

где H₀ = 273R_c/g₀ — высота однородной атмосферы при t = 0 °С.

Проинтегрируем (3.3.19) в пределах от высоты z₁, где давление равно p₁, до высоты z₂, где давление равно р₂. Для величин t, s и z в правой части (3.3.19) при интегрировании введем средние значения (на основании известной теоремы о среднем). Выполнив интегрирование, получим:

полная барометрическая формула (формула Лапласа) окончательно принимает вид

Величина В = 2,30Н₀ ≈ 18 400 м называется барометрической постоянной, а средние значения и носят название средних баро­метрических (температуры и доли водяного пара соответственно).

В таком полном виде барометрическая формула на практике ис­пользуется лишь при барометрическом нивелировании. При реше­нии подавляющего большинства метеорологических задач такой высокой точности, какую может обеспечить формула Лапласа, не требуется. К тому же следует иметь в виду, что точность измерения исходных данных (температуры, влажности, давления), необходи­мых для выполнения расчетов по формуле (3.3.21), как правило, значительно меньше тех уточнений, которые дает формула Лапласа по сравнению с приводимой ниже барометрической формулой ре­альной атмосферы. Последняя получается из формулы (3.3.21), если считать воздух сухим (s = 0) и пренебречь зависимостью уско­рения свободного падения от широты и высоты:

Возвращаясь к натуральным логарифмам и абсолютной темпера­туре, формулу (3.3.22) можно переписать в виде

где = 273(1 + a ) — средняя барометрическая температура слоя воздуха, заключенного между уровнями z₁ и z₂. Из сравнения по­следней формулы с формулой (3.3.3) следует, что средняя барометрическая температура связана с температурой воздуха следующим образом:

Средняя барометрическая температура — это такая постоянная в пределах слоя температура, которая обеспечивает значения давле­ния на границах его, наблюдаемые при реальном распределении температуры по высоте. Практически Т нередко отождествляют со средней арифметической температурой, т. е. полагают

где Т₁ и Т₂ — температуры воздуха на нижней и верхней границах слоя. Если уровень z₁ совпадает с поверхностью Земли (z₁ = 0), а уровень z₂ — произвольный (z₂ = z), то формула (3.3.23) принимает вид

Эта формула имеет такой же вид, как и барометрическая форму­ла (3.3.12) изотермической атмосферы. Принципиальное различие состоит в том, что формулы (3.3.20), (3.3.23) и (3.3.25) всегда спра­ведливы лишь для слоя заданной конечной толщины, для которого температура должна быть каждый раз определена прежде, чем по формулам можно начинать выполнять расчет. Вместе с изменением толщины слоя изменяется и величина . В случае же изотермиче­ской атмосферы температура является независимой (задаваемой) величиной. Поскольку барометрическая формула реальной атмо­сферы является показательной функцией, на основе ее анализа можно сделать такие же выводы относительно закономерностей из­менения давления с высотой, какие были сделаны в случае изотер­мической атмосферы. Роль температуры T₀ в реальной атмосфере играет средняя барометрическая температура . Все выводы в слу­чае реальной атмосферы относятся к слою конечной толщины. Поэ­тому вывод о бесконечной протяженности атмосферы, сделанный на основе формулы (3.3.12), здесь отпадает.

Если необходимо учесть влияние влажности на плотность возду­ха и распределение давления по высоте, то в формулах (3.3.22) — (3.3.25) средняя барометрическая температура должна быть заме­нена средней виртуальной барометрической температурой _υ.

Атмосферное давление — измеряется весом (пропорционально массе) вышележащего столба воздуха на единицу горизонтальной поверхности.

Атмосферное давление и ветер.

Атмосферное давление выражается либо в гектопаскалях (гПа), численно равных миллибарам (мб), либо в миллиметрах ртутного столба (мм рт. ст.).

Распределение атмосферного давления называют барическим полем. Атмосферное давление есть величина скалярная: в каждой точке атмосферы оно вполне характеризуется одним числовым значением, выраженным в миллибарах или миллиметрах ртутного столба.

Как всякое скалярное поле, его можно наглядно представить в пространстве поверхностями равных значений данной величины, а на плоскости — линиями равных значений – изобар.

В случае атмосферного давления это будут изобарические поверхности и изобары.

Изобарическая поверхность со значением 1000 мб проходит вблизи уровня моря. Изобарическая поверхность 700 мб располагается на высотах, близких к 3 км, изобарическая поверхность 500 мб—на высотах, близких к 5 км. Изобарические поверхности 300 и 200 мб располагаются соответственно на высотах около 9 и около 12км, т.е. вблизи тропопаузы.

Изобарические поверхности наклонены относительно поверхностей уровня, в том числе и уровня моря. Поэтому в разных своих точках каждая изобарическая поверхность в каждый момент находится на различных высотах над уровнем моря.

Плотность воздуха ρ зависит от температуры, влажности и давления.

Эта зависимость определяется известными из физики газовыми законами, основным уравнением газового состояния Клайперона и состоит в следующем:

1) чем выше температура в-ха, тем меньше плотность;

2) чем больше влажность воздуха, тем меньше его плотность;

3) чем больше давление, под которым находится тот или иной объем воздуха, тем больше его плотность.

Изменение давления с высотой

Неподвижная по отношению к Земле атмосфера подвержена силе тяготения. Изменение давления с высотой в условиях статического равновесия, т.е. когда воздух находится в покое описывается основным

уравнением статики атмосферы, связывающим давление воздуха р, плотность p, ускорение свободного падения g и высоту z

dp = -ρg dz

g=980,616 см/с 2 R_c – удельная газовая постоянная 2,87 х 10 3 Дж/(кг 0 С)

или изменение атмосферного давления с высотой

Из этого уравнения можно сделать следующие выводы;

1. В атмосфере давление с увеличением высоты всегда убывает.

2. Атмосферное давление на каждом уровне представляет собой вес столба воздуха с поперечным сечением 1м 2 и высотой от данного уровня до верхней границы атмосферы.

3. При подъеме на одну и ту же высоту (dz=const) уменьшение давления

(- dp) тем больше, чем больше плотность воздуха ρ иускорение свободного падения g, которое играет второстепенную роль.

Поскольку плотность убывает с высотой, то чем выше расположен уровень, тем меньше убывание давления при подъеме на одну и ту же высоту dz.

Барометрические формулы.

Барометрические формулы – интегралы основного уравнения статики атмосферы, полученные при разных предположениях относительно изменения температуры и плотности воздуха с высотой.

С помощью этих формул решается целый ряд практических задач:

— определяется превышение одного уровня zнад другим, если известны давление и температура на этих двух уровнях;

— определяется давление на нижнем уровне, если известны высота, давление и температура(приведение к уровню моря);

— определяется давление на какой-либо высоте, если известны высота, давление и температура на нижнем уровне (уровне моря).

Путем интегрирования обеих частей основного уравнения статики получают различные барометрические формулы:

Барометрическая формула однородной атмосферы ( плотность воздуха в пределах всей атмосферы с высотой не изменяется) –

Высота однородной атмосферы зависит от температуры воздуха у поверхности Земли. При t=0 0 она составляет примерно 8 км.

Барометрическая формула изотермической атмосферы (атмосфера, в которой температура с высотой остается неизменной, dt=const)

Барометрическая формула политропной атмосферы (атмосфера, в которой предполагается линейное изменение температуры с высотой или постоянное значение вертикального градиента температуры.

В политропной атмосфере при одних и тех же значениях давления и температуры, давление убывает с высотой тем быстрее, чем больше значение

вертикального градиента температуры (y ).

Полная барометрическая формула атмосферы – она получена для общего случая, т.е. для произвольного распределения температуры по высоте, влажного воздуха и изменения ускорения свободного падения в зависимости от широты места и высоты (используется только при барометрическом нивелировании)

При решении большинства метеорологических задач используют более простую формулу – барометрическую формулу реальной атмосферы ( воздух сухой, а ускорение свободного падения не зависит от широты места и высоты).

При определении высоты точки по измеренному давлению и расчете распределения давления в ограниченном слое атмосфере (не более 2000м)

используется Барометрическая формула Бабине

α=0,004 коэф. теплового расширения газов

Для приближенной оценки высоты по известной разности давлений или, наоборот, для оценки давления по заданной разности высот пользуются понятием «барическая ступень».

Барической ступенью называется такая высота h, на которую нужно подняться (опуститься) от (до) исходного уровня, чтобы давление понизилось (повысилось) на 1 гПа, с увеличением высоты барическая ступень растет.

Дата добавления: 2016-01-30 ; просмотров: 2366 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

«АТМОСФЕРНОЕ ДАВЛЕНИЕ И ПЛОТНОСТЬ ВОЗДУХА. СТАТИКА АТМОСФЕРЫ» ОБЩИЙ ХАРАКТЕР РАСПРЕДЕЛЕНИЯ в АТМОСФЕРЕ ТЕМПЕРАТУРЫ

Температура воздуха в каждой точке атмосферы непрерывно меняется, в разных местах Земли в одно и тоже же время по-разному. У земной поверхности температура воздуха варьируется в довольно широких пределах: в тропических пустынях до + 60 °С, на материке Антарктика до – 90 °С.

С высотой температура воздуха изменяется в разных слоях и в разных широтах по-разному. В среднему она сначала снижается до высоты 10-15 км, а потом – растет до высоты 50-60 км, потом снова – падает. Чтобы определить температуру на любом уровне Z ввели понятия вертикального градиента температуры.

Вертикальным градиентом температуры воздуха называют ее изменение на каждые 100 г высоты.

где z_в – высота верхнего уровня, м;

z_н – высота нижнего уровня, м.

Данные о вертикальном градиенте температуры в разных пластах атмосферы используются при составлении прогнозов погоды, метеообслуживании полетов реактивных самолетов. Зная вертикальный градиент температуры, легко определить температуру t_z на любом уровне z, если известна температура t₀ на нижнем уровне:

Можно также определить температуру на нижнем уровне, если известная температура на высоте z. Такую задачу решают для приведения температуры к уровню моря. Средний по высоте и времени вертикальный градиент температуры в тропосфере составляет 0,6 °С/100 г.

График зависимости температуры воздуха от высоты, называется кривой стратификации.

УРАВНЕНИЕ СОСТОЯНИЯ СУХОГО И ВЛАЖНОГО ВОЗДУХА

Плотность воздуха непосредственно не определяется, а вычисляется при помощи уравнения состояния газа. Для одного моля газа:

где R – универсальная газовая постоянная. При нормальных условиях: Р = 101330 н/м 2 , T =273 К, R = 287,05 Дж/(кг·град).

По уравнению (3.3) можно определить плотность сухого воздуха. При н.у. ρ_в = 1,293 кг/м 3 .

Теперь найдем выражение для плотности влажного воздуха с температурой T, давлением воздуха Р і давлением водного пара е.

Влажный воздух – это смесь сухого воздуха и водяного пара.

где Р ’ – давление сухого воздуха.

Поэтому, давление сухого воздуха равняется (Р – е).

Для сухого воздуха уравнения состояния запишется в таким образом:

Для водяного пара:

Коэффициент 0,622 – это отношения молярной массы водяного пара к молярной массе сухого воздуха.

Общая плотность влажного воздуха равняется сумме плотности сухого воздуха и водного пара:

Тогда уравнение состояния влажного воздуха запишется так:

R_в – газовая постоянная для сухого воздуха, равная 287 Дж/(кг·град);

R_п – газовая постоянная для влажного воздуха, равная 460 Дж/(кг·град).

Отношение е/Р мало, поэтому можно записать так:

Тогда, уравнение состояния для влажного воздуха примет вид:

Величина называется виртуальной температурой (T_v).

то есть плотность влажного воздуха описывается уравнением состояния сухого воздуха, но только с заменой температуры T на виртуальную температуру T_v.

Виртуальная температура влажного воздуха T_v – это такая температура, какую должен был бы иметь сухой воздух, чтобы его плотность равнялась плотности влажного воздуха с температурой T, давлением Р и давлением водяного пара е.

Виртуальная температура всегда немного выше истинной температуры влажного воздуха.

Плотность воздуха в каждом месте непрерывно изменяется во времени. Кроме того, она меняется с высотой, так как с высотой меняется также атмосферное давление и температура воздуха. Давление с высотой всегда уменьшается, а вместе с ним убывает и плотность. Температура с высотой, в основной, снижается, по крайней мере, в нижних слоях (10-15 км) атмосферы. Но падение температуры вызывает повышение плотности. В результате общего влияния изменения давления и температуры плотность с высотой, как правило, снижается, но не так сильно, как давление. В среднем для Европы она равняется у земной поверхности 1,25 кг/м 3 ; на высоте 5 км – 0,74 кг/м 3 ; 10 км – 0,41 кг/м 3 ; 20 км – 0,09 кг/м 3 .

ИЗМЕНЕНИЕ ДАВЛЕНИЯ ВОЗДУХ С ВЫСОТОЙ. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА

По какому закону меняется атмосферное давление с высотой?

Допустим, что известно давление на одном уровне. Какое оно в тот же момент на другом уровне? Возьмем вертикальный столб воздуха с поперечным разрезом, равным единице, и выделим в этом столбе тонкий слой, ограниченный снизу поверхностью на высоте Z , а сверху – поверхностью на высоте (Z+dZ). Толщина слоя dZ.

Рисунок 3.1 – Силы, которые действуют на элементарный объем воздуха

На нижнюю поверхность выделенного элементарного объема соседний воздух действует с силой давления, которая направленная снизу вверх. Модуль этой силы на рассмотренной поверхности площадью, равной единице, и будет давлением воздуха Р на этой поверхности. На верхнюю поверхность элементарного объема соседний воздух действует с силой давления, которая направлена сверху вниз. Модуль этой силы P+dP есть давление на верхней границе. Это давление отличается от давления на нижней границе на маленькую величину dр, причем заранее не известно, будет dр положительным или отрицательной, то есть будет давление на верхней границе выше или ниже, чем на нижней границе.

Что касается сил давления, которые действуют на боковые стенки объема, то допустим, что в горизонтальном направлении атмосферное давление не меняется. Это значит, что силы давления, которые действуют со всех сторон на боковые стенки, уравновешиваются: их равнодействующая равняется нулю. Отсюда вытекает, что воздух в горизонтальном направлении не имеет ускорения и не перемещается.

Кроме того, на рассмотренный элементарный объем действует сила тяжести, которая направленная вниз и равняется ускорению свободного падения g, умноженному на массу воздуха во взятом объеме. Поэтому при вертикальном разрезе, равном единице, объем равняется dz, масса воздуха в нем равняется ρdz, где ρ – плотность воздуха, а сила тяжести равняется gρdz.

Сила тяжести gρdz и сила давления Р+dp направлены вниз; возьмем их с отрицательным знаком. Вверх направлена сила давления Р, ее возьмем с знаком “ + “.

В состоянии равновесия:

— ( Р + dp ) + Р – gρdz = 0

или dр = – gρdz (3.4)

Отсюда следует, что при движении вверх атмосферное давление падает.

Уравнение (3.4) называется основным уравнением статики атмосферы.

— gp = 0

— – падение давления на единицу прироста высоты, то есть вертикальный барический градиент (вертикальный градиент давления).

— вертикальный барический градиент, отнесенный к единице массы и направленный вверх.

Основное уравнение статики выражает условие равновесия между двумя силами, которые действуют на единицу массы воздуха по вертикали – вертикальным барическим градиентом и силой тяжести.

Чтобы получить уравнение для изменения давления при конечном приросте высоты нужно проинтегрировать уравнение (3.4) в пределах от уровня z₁ до z₂ с давлением от Р₁ до Р₂. При этом плотность воздуха ρ есть переменной величиной, функцией высоты.

dp = – dz ли

= – dz (3.5)

Проинтегрируем уравнение (3.5)

ln p₂ – ln p₁ = —

Температура – величина перемена, зависит от высоты. Но эта зависимость не может быть точно описана математической функцией. Поэтому, берут среднее значение температуры T_m между уровнями z₁ и z₂. Тогда среднюю температуру можно вынести за знак интеграла.

ln p₂ – ln p₁ = —

ln = – ( z₂ – z₁ ) (3.6)

Потенцируем уравнения 3.6, и получим:

Уравнение (3.7) называется барометрической формулой.

Эта формула показывает, как меняется атмосферное давление с высотой в зависимости от температуры воздуха.

С помощью барометрической формулы можно решить три задачи:

1. зная давление на одном уровне и среднюю температуру слоя воздуха, найти давление на другом уровне;

2. зная давление на обоих уровнях и среднюю температуру слоя воздуха, найти разность уровней (барометрическое нивелирование );

3. зная разность уровней и значения давления на них, найти среднюю температуру слоя воздуха.

В случае расчетов для влажного воздуха берется значение R для сухого воздуха, умноженное на (1 + 0,378) .

Важным вариантом первой задачи есть приведение давления к уровню моря. Зная давление на некоторой станции, расположенной на высоте Z над уровнем моря, и температуру t на этой станции, вычисляют сначала среднюю температуру на рассмотренной станции и на уровне моря. Для уровня станции берется фактическая температура, а для уровня моря – та же температура, но увеличенная в той мере, в которой в среднем меняется температура воздуха с высотой. Средний вертикальный градиент температуры в тропосфере принимается равным 0,6 °С /100 г.

Итак, если станция имеет высоту 200 м и температура на ней 16 °С, то для уровня моря температура принимается равной 17,2 °С , а средняя температура составит 16,6 °С. После этого по давлению на станции и по полученной средней температуре определяется давление на уровне моря. Приведение давления к уровню моря необходимо потому, что на приземные карты погоды всегда наносится давление, приведенное к уровню моря. Этим исключается влияние расхождений в высотах станций на значение давления и становится возможной выяснить горизонтальное распределение давления.

ВЕРТИКАЛЬНЫЙ ГРАДИЕНТ ДАВЛЕНИЯ

Вертикальный градиент давления – это изменение давления при перемещении на единицу высоты.

Основное уравнение статики:

где ρ – средняя плотность воздуха в слое ∆z, кг/м 3 ;

∆Р – изменение давления при изменении высоты, гПа.

Разделим обе части уравнения статики на ∆z.

Вертикальный градиент давления выражается в гПа/100 г.

Барическая ступень – высота, на которую нужно подняться или опуститься, чтобы давление изменилось на 1 гПа.

Барическая ступень (м/гПа) – величина, обратная вертикальному градиенту давления.

h = RT/g = [2,87 · 10 6 (273,15 + t)]/(980,6*P) ≈ 8000 (1+αt)/P, (м/гпа),

α – коэффициент температурного расширения, равный 0,004. (1/273=0,004).

Если пренебречь незначительными изменениями ускорения силы тяжести, то барическая ступень зависит только от плотности воздуха. Так как плотность воздуха с высотой уменьшается, то барическая ступень при увеличении высоты растет. При одном и того же давлении Р барическая ступень большее в теплом воздухе, чем в холодном.

При температуре 0 0 С и давлении 1000 гПа барическая ступень равняется 8 м/гПа. При повышении температуры барическая ступень увеличивается в (1+αt) раз, то есть на 0,4 % на каждый градус нагревания.

В метеорологии принято понятие Международной стандартной атмосферы. В Международной стандартной атмосфере значения давления, температуры и других параметров рассчитаны к высотам 200 км. За начальный уровень принят уровень моря, на котором давление считается равным 1013,3 гПа, а температура воздуха 15 °С. К высоте 11 км стандартная атмосфера политропная (температура с высотой изменяется линейно) и имеет вертикальный градиент температуры 0,65 °С/100 г, от 11 до 30 км она является изотермической и имеет температуру (-56,5 °С).

Однородная атмосфера

Однородная атмосфера – это слой воздуха, где плотность воздуха не изменяется с высотой. В однородной атмосфере изменение давления с высотой определяется соотношением:

где Р₁ и Р₂ – давление на высотах z₁ и z₂ соответственно;

r – плотность воздух, кг/м 3 ;

g – ускорение свободного падения, м/с 2 .

Изотермическая атмосфера

Изотермическая атмосфера – это слой воздуха, где температура воздуха не изменяется с высотой.

В изотермической атмосфере изменение давления с высотой определяется соотношением:

Политропная атмосфера

Политропная атмосфера – это слой воздуха, где температура воздуха с высотой изменяется линейно, то есть вертикальный градиент температуры имеет постоянную величину.

В политропной атмосфере изменение давления с высотой определяется соотношением

где g – вертикальный градиент температуры, 0 С/100 г;

Т₁ – температура (R) на высоте z₁ (м).

Реальная атмосфера

Формула Лапласа есть одним из интегралов основного уравнения статики. Она имеет вид:

z₂ – z₁ = 18400 (1 + at) (1 +0,378 e/p) (1 + 0,0026 cosj) (1 + bz) lg Р₁/Р₂, (3.11)

где Р₁ и Р₂ – давление на уровнях z₁ и z₂; z = (z₁ + z₂) /2 – высота над уровнем моря рассмотренного пули;

t, e, Р – средние по высоте значения температуры ( 0 С), парциального давления водной пари и атмосферного давления в рассмотренном пласте;

j – широта места;

b – коэффициент, равный 3,14*10 -7 г -1 для горных местностей;

α – коэффициент, равный 0,004;

множитель (1+0,378 e/p) учитывает влажность воздуха;

множители (1+ 0,0026 cosj) и (1 + β·z) характеризуют зависимость ускорения свободного падения от широты и высоты места над уровнем моря.

На практике часто пользуются сокращенной формулой Лапласа;