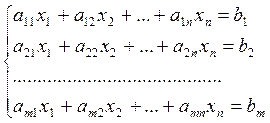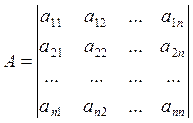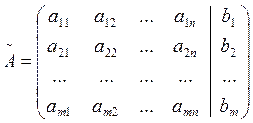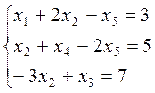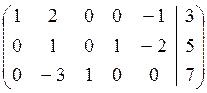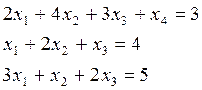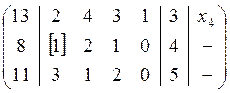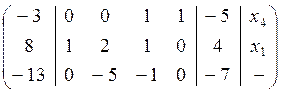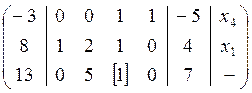Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.
Что означает фраза «ранг матрицы равен $r$»? Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют.
Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.
Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $\widetilde$.
Решить СЛАУ $ \left \ < \begin
Итак, мы имеем СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:
$$ \left( \begin
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.
И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $\rang A=\rang\widetilde = 2$.
Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).
Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:
На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $\left( \begin
Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:
$$ M_<2>^<(1)>=\left| \begin
Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.
Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №3 и №4:
$$ M_<2>^<(2)>=\left| \begin
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №3 (он соответствует переменной $x_3$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_3$ и $x_4$ можно принять в качестве базисных.
Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.
Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_
В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.
Базисные переменные выбраны: это $x_1$ и $x_3$. Остальные $n-r=2$ переменных (т.е. $x_2$ и $x_4$) являются свободными. Нам нужно выразить базисные переменные через свободные.
Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $\left( \begin
$$ \left( \begin
Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:
Почему меняются знаки? Что вообще значит это перенесение столбцов? показать\скрыть
Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $\left( \begin
Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
$$ \left( \begin
Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Если вспомнить, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, то получим:
Нами получено общее решение заданной СЛАУ. Чтобы найти базисное решение, нужно все свободные переменные приравнять к нулю. Т.е. полагая $x_2=0$ и $x_4=0$, будем иметь:
Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $\left\ <\begin
Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-\frac<1><3>x_4$ и $x_3=-2-\frac<4><3>x_4$ в левую часть первого уравнения, получим:
$$ 3x_1-6x_2+9x_3+13x_4=3\cdot \left(9+2x_2-\frac<1><3>x_4\right)-6x_2+9\cdot \left(-2-\frac<4><3>x_4\right)+13x_4=9. $$
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Если система является неопределённой, указать базисное решение.
Похожий пример уже был решен в теме «метод Крамера» (пример №4). Переменные $x_4$ и $x_5$ были перенесены в правые части, а дальше применялись стандартные операции метода Крамера. Однако такой метод решения не гарантирует достижения результата. Например, мы переносим некие переменные в правую часть, а оставшийся определитель оказывается равным нулю, – что тогда? Решать перебором? 🙂 Поэтому гораздо удобнее применять преобразования метода Гаусса, как и в предыдущем примере.
$$ \left( \begin
Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $\rang A=\rang\widetilde = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.
Количество неизвестных $n=5$, ранги обеих матриц $r=3$, поэтому нужно выбрать три базисных переменных и $n-r=2$ свободных переменных. Применяя тот же метод «ступенек», что и в предыдущем примере, выберем в качестве базисных переменных $x_1$, $x_2$, $x_3$, а в качестве свободных переменных – $x_4$ и $x_5$.
Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:
$$ \left( \begin
Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.
Размерность и базис линейного пространства
Определения размерности и базиса
Линейное пространство называется n-мерным , если в нем существует система из линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число называется размерностью (числом измерений) линейного пространства и обозначается . Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве найдется система, состоящая из линейно независимых векторов, то такое пространство называют бесконечномерным (записывают: ). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.
Базисом n-мерного линейного пространства называется упорядоченная совокупность линейно независимых векторов ( базисных векторов ).
Теорема 8.1 о разложении вектора по базису. Если — базис n-мерного линейного пространства , то любой вектор может быть представлен в виде линейной комбинации базисных векторов:
и притом единственным образом, т.е. коэффициенты определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
Действительно, размерность пространства равна . Система векторов линейно независима (это базис). После присоединения к базису любого вектора , получаем линейно зависимую систему (так как это система состоит из векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.
Следствие 1. Если — базис пространства , то , т.е. линейное пространство является линейной оболочкой базисных векторов.
В самом деле, для доказательства равенства двух множеств достаточно показать, что включения и выполняются одновременно. Действительно, с одной стороны, любая линейная комбинация векторов линейного пространства принадлежит самому линейному пространству, т.е. . С другой стороны, любой вектор пространства по теореме 8.1 можно представить в виде линейной комбинации базисных векторов, т.е. . Отсюда следует равенство рассматриваемых множеств.
Следствие 2. Если — линейно независимая система векторов линейного пространства и любой вектор может быть представлен в виде линейной комбинации (8.4): , то пространство имеет размерность , а система является его базисом.
В самом деле, в пространстве имеется система линейно независимых векторов, а любая система из большего количества векторов n)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAEAAAAAWBAMAAACCkIcHAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAAX1hEMCpIZfQQeAxUfDvHPe4AAABRklEQVQoz2NgIAyYD+CS4TUAU2YMDBbBWBUwxoJI9icMDFd/YTfCuwBIsCowMLB9xK6ALQFInHdgYJAOBPOZFqIpYP8OJDoFGBjqFcB8Fk1DNEc8AuIIIMN+gUcMigqWtgNmQBcypgHxJyA/XyYrDCKhrQKmOVY8M9QHel8PqOAvEG894fQJaqglWIWk2C+G9QsYGPUFGNiBPmT/2cCyAGatZQuQrJUOYACZYC/AwAJUwPz1GTw0GU1TQFS9AmO0AFgByAq2j94T4Aa0g2n7BSw/gBTQCpAjpQNYNxpBHAlxAtDZAsx/PBkYgY5kiACZxxoQDvEmVJ5xKwPHA2UGhlQgW1MA6F7mZwaoAfWJgfdHAwPjJpBzHBh4GBjcwb5HBCQwllygQS2mgDupcAQACZ4tuBX4FUATDC4ASUdMF3DJMxkQkWIB7TREH/AzV/MAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы . Значит, и — базис .
Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему векторов n-мерного линейного пространства можно дополнить до базиса пространства.
В самом деле, пусть — линейно независимая система векторов n-мерного пространства . Рассмотрим линейную оболочку этих векторов: . Любой вектор образует с векторами линейно зависимую систему , так как вектор линейно выражается через остальные. Поскольку в n-мерном пространстве существует линейно независимых векторов, то и существует вектор , который не принадлежит . Дополняя этим вектором линейно независимую систему , получаем систему векторов , которая также линейно независимая. Действительно, если бы она оказалась линейно зависимой, то из пункта 1 замечаний 8.3 следовало, что , а это противоречит условию . Итак, система векторов линейно независимая. Значит, первоначальную систему векторов удалось дополнить одним вектором без нарушения линейной независимости. Продолжаем аналогично. Рассмотрим линейную оболочку этих векторов: . Если , то — базис и теорема доказана. Если , то дополняем систему вектором и т.д. Процесс дополнения обязательно закончится, так как пространство конечномерное. В результате получим равенство , из которого следует, что — базис пространства . Теорема доказана.
1. Базис линейного пространства определяется неоднозначно. Например, если — базис пространства , то система векторов при любом также является базисом . Количество базисных векторов в разных базисах одного и того же конечномерного пространства, разумеется, одно и то же, так как это количество равно размерности пространства.
2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.
3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.
4. Если множество является линейной оболочкой , то векторы называют образующими множества . Следствие 1 теоремы 8.1 в силу равенства позволяет говорить, что базис — это минимальная система образующих линейного пространства , так как нельзя уменьшить количество образующих (удалить хотя бы один вектор из набора ) без нарушения равенства .
5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.
6. Следствие 2 теоремы 8.1 удобно применять для нахождения базиса и размерности линейного пространства. В некоторых учебниках оно берется за определение базиса, а именно: линейно независимая система векторов линейного пространства называется базисом, если любой вектор пространства линейно выражается через векторы . Количество базисных векторов определяет размерность пространства . Разумеется, что эти определения эквивалентны приведенным выше.
Примеры базисов линейных пространств
Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.
1. Нулевое линейное пространство не содержит линейно независимых векторов. Поэтому размерность этого пространства полагают равной нулю: . Это пространство не имеет базиса.
2. Пространства имеют размерности 1, 2, 3 соответственно. Действительно, любой ненулевой вектор пространства , образует линейно независимую систему (см. пункт 1. замечаний 8.2), а любые два ненулевых век тора пространства коллинеарны, т.е. линейно зависимы (см. пример 8.1). Следовательно, , а базисом пространства является любой ненулевой вектор. Аналогично доказывается, что и . Базисом пространства служат любые два неколлинеарных вектора, взятые в определенном порядке (один из них считается первым базисным вектором, другой — вторым). Базисом пространства являются любые три некомпланарных (не лежащих в одной или параллельных плоскостях) вектора, взятые в определенном порядке. Стандартным базисом в является единичный вектор на прямой. Стандартным базисом в считается базис , со стоящий из двух взаимно перпендикулярных единичных векторов плоскости. Стандартным базисом в пространстве считается базис , составленный из трех единичных попарно перпендикулярных векторов, образующих правую тройку.
3. Пространство содержит не более, чем , линейно независимых векторов. В самом деле, возьмем столбцов из и составим из них матрицу размеров . Если n» png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQCAMAAACIsme9AAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMActEwobEQRsAhMfCRYeCBZdtIVwAAAMRJREFUKM+dkdsSwyAIRJUKivHC/39tJY6Npplm0jxEHT3A7hrzx/dyAZ8RnOUhYaLYh4SVOA9Z+ZbAbTn64O6YDfVZWhhvzlWIU/t9ZCSblkbehZkhJEHHBDhkpGhkOzk4MzazQFtDf4SCTXmkL9ddGYynLLovocsAKFf2coKji5MjBl1Wf8dUeTru1ZPwSMO3nrCEuio3LFUxaIpUhlHC19lLPLnbZUglrVuaY822QL8SrLtJGECn77dxGugicer19OYNWVcGI0RZra4AAAAASUVORK5CYII=» />, то столбцы линейно зависимы по теореме 3.4 о ранге матрицы. Следовательно, . В пространстве не трудно найти п линейно независимых столбцов. Например, столбцы единичной матрицы
линейно независимы. Следовательно, . Пространство называется n-мерным вещественным арифметическим пространством . Указанный набор векторов считается стандартным базисом пространства . Аналогично доказывается, что , поэтому пространство называют n-мерным комплексным арифметическим пространством .
4. Напомним, что любое решение однородной системы можно представить в виде , где , a — фундаментальная система решений. Следовательно, , т.е. базисом пространства решений однородной системы служит ее фундаментальная система решений, а размерность пространства , где — количество неизвестных, а — ранг матрицы системы.
5. В пространстве матриц размеров можно выбрать 6 матриц:
которые линейно независимы. Действительно, их линейная комбинация
равна нулевой матрице только в тривиальном случае . Прочитав равенство (8.5) справа налево, заключаем, что любая матрица из линейным образом выражается через выбранные 6 матриц, т.е. . Следовательно, , а матрицы являются базисом (стандартным) этого пространства. Аналогично доказывается, что .
6. Для любого натурального в пространстве многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены линейно независимы, так как их линейная комбинация
равна нулевому многочлену только в тривиальном случае . Поскольку эта система многочленов линейно независима при любом натуральном л, пространство бесконечномерное. Аналогично делаем вывод о бесконечной размерности пространства многочленов с действительными коэффициентами. Пространство многочленов степени не выше, чем , конечномерное. Действительно, векторы образуют базис (стандартный) это го пространства, так как они линейно независимы и любой многочлен из можно представить в виде линейной комбинации этих векторов:
7. Пространство непрерывных функций является бесконечно мерным. Действительно, для любого натурального многочлены , рассматриваемые как непрерывные функции, образуют линейно независимые системы (см. предыдущий пример).
В пространстве тригонометрических двучленов (частоты ) с действительными коэффициентами базис образуют одночлены . Они линейно независимы, так как тождественное равенство возможно только в тривиальном случае . Любая функция вида линейно выражается через базисные: .
8. Пространство действительных функций, определенных на множестве , в зависимости от области определения может быть конечномерным или бесконечномерным. Если — конечное множество, то пространство конечномерное (например, ). Если — бесконечное множество, то пространство бесконечномерное (например, пространство последовательностей).
9. В пространстве любое положительное число , не равное единице, может служить базисом. Возьмем, например, число . Любое положительное число можно выразить через , т.е. представить в виде , где . Следовательно, размерность этого пространства равна 1, а число является базисом.
10. Пусть — базис вещественного линейного пространства . Определим на линейные скалярные функции , положив:
При этом, в силу линейности функции , для произвольного вектора получаем .
Итак, определены элементов (ковекторов) сопряженного пространства . Докажем, что — базис .
Во-первых, покажем, что система линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов и приравняем ее нулевой функции
Подставляя в это равенство , получаем . Следовательно, система элементов пространства линейно независима, так как равенство возможно только в тривиальном случае.
Во-вторых, докажем, что любую линейную функцию можно представить в виде линейной комбинации ковекторов . Действительно, для любого вектора в силу линейности функции получаем:
т.е. функция представлена в виде линейной комбинации функций (числа — коэффициенты линейной комбинации). Следовательно, система ковекторов является базисом сопряженного пространства и (для конечномерного пространства ).
Системы линейных уравнений. Основные понятия. Переменные, входящие в уравнения системы
Страницы работы
Содержание работы
Глава 7 Системы линейных уравнений.
Определение 1:Системой линейных уравнений называется система вида:
Определение 2: Решением системы линейных уравнений называется упорядоченный набор чисел 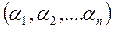
Определение 3: Основной матрицей системы линейных уравнений называется матрица А размерности 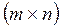
Определение 4: Основная матрица А системы дополненная столбцом свободных членов, называется расширенной матрицей системы и обозначается 
Определение 5: Система уравнений называется совместной, если она имеет хотя бы одно решение и несовместной если у неё нет.
Определение 6: Система уравнений называется однородной, если все свободные члены равны нулю.
Определение 7: Неизвестная хi в системе линейных уравнений называется базисной, если она встречается в единственном уравнении системы и имеет коэффициент равный единице.
Определение 8: Система уравнений имеет базисный вид, то есть приведена к единичному базису, если в каждом уравнении выделена одна базисная переменная.
Приведём системы базисного вида:
Расширенная матрица этой системы:
Нетрудно увидеть, что базисными переменными в приведённом примере являются переменные х1, х3, х4.
Определение 9: Переменные входящие в уравнения системы и не являющиеся базисными называются свободными переменными.
Определение 10: Две системы линейных уравнений называются равносильными, если множества их решений совпадают. Все несовместные системы равносильны.
Перечислим элементарные преобразования систем, приводящие к равносильным системам:
2. Умножение на число 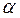
3. Прибавление к левой и правой части i-ого уравнения соответствующих частей j – ого уравнения, умноженных на число 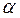
4. Перестановка местами i-ого и j-ого уравнений.
7.2 Решение системы линейных уравнений методом Жордана-Гаусса.
Этот метод позволяет привести к базисному виду совместную систему уравнений.
Элементарные преобразования будем осуществлять по следующей схеме.
1. Выбираем разрешающий элемент в каком либо уравнении и если этот элемент расширенной матрицы не является единицей, то элементы разрешающей строки делим на этот элемент.
2. Разрешающий столбец с помощью элементарных преобразований заполняем нулями.
3. Получаем новую расширенную матрицу, в которой снова выбираем другую разрешающую строку и повторяем все действия.
4. В случае возникновения нулевой строки ее вычеркиваем.
5. В случае возникновения строки вида: 0х1+0х2+0хn=bi система не имеет решений, то есть является несовместной.
Рассмотрим пример решения системы с использованием столбца контрольных сумм КΣ, которые представляют собой суммы всех коэффициентов, соответствующих уравнений. Эти числа преобразуются по тем же правилам, что и остальные элементы матрицы. Контроль состоит в том, что на каждом этапе проверяется совпадение контрольной суммы с суммой всех коэффициентов данного уравнения. Решим систему уравнений.
Составим расширенную матрицу системы, причем в первом столбце будут контрольные суммы, а в последнем будем указывать базисные переменные. Легко видеть что в первом уравнении такой переменной будет переменная х4.
выберем разрешающий элемент во второй строке, пусть это будет 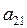
1. Разрешающая строка умножается на (-2) и складывается с первой строкой, результат записываем на место первой строки.
2. Разрешающая строка умножается на (-3) и складывается с третьей строкой, результат записывается на место третьей строки.
В результате получаем матрицу:
Используя столбец контрольных сумм, сделаем проверку:
Следующим шагом необходимо выбрать разрешающий элемент в третьей строке. В качестве такого элемента можно взять элемент 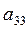
используя элементарные преобразования, преобразуем разрешающий столбец матрицы так, чтобы все элементы кроме разрешающего (базисного) стали равны нулю, для этого выполняем следующие элементарные преобразования.
1. Разрешающая строка умножается на (-1) и складывается со второй строкой, результат записывается на место второй строки.
2. Разрешающая строка умножается на (-1) и суммируется с первой строкой, результат записывается на место первой строки.
http://mathhelpplanet.com/static.php?p=razmernost-i-bazis-linyeinogo-prostranstva
http://vunivere.ru/work70872