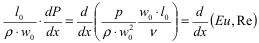Безразмерные переменные и уравнения подобия

Безразмерные переменные (числа подобия) и уравнения

Подобия

Помимо безразмерных величин θ, W_XiW_y и безразмерных координат, составленных из однородных физических величин, в уравнения входят также безразмерные комплексы, состоящие из разнородных физических величин:

Этим комплексам, называемым числами подобия, присвоены имена ученых, внесших значительный вклад в развитие гидродинамики или теплопередачи.

1. Первый из этих безразмерных комплексов обозначают

и называют числом Нуссельта, или безразмерным коэффициентом теплоотдачи. Число Нуссельта характеризует теплообмен на границе стенка — жидкость. В задачах конвективного теплообмена число Nuобычно искомая величина, поскольку в него входит определяемая величина а.

Несмотря на внешнее сходство с числом Био (Bi)

используемым при изучении теплопроводности, число Нуссельта существенно отличается от него. В число Bi входит коэффициент теплопроводности твердого тела; в число Nu — коэффициент теплопроводности жидкости. Кроме того, в число Био коэффициент теплоотдачи вводится как величина, заданная в условиях однозначности, мы же рассматриваем коэффициент теплоотдачи, входящий в Nu, как величину искомую.

2. Безразмерный комплекс

называют числом Рейнольдса. Оно характеризует соотношение сил инерции и сил вязкости. Число Рейнольдса – важная характеристика как изотермического, так и неизотермического процессов течения жидкости.

3. Третий безразмерный комплекс обозначают

и называют числом Пекле. Его можно преобразовать следующим образом:

Здесь числитель характеризует теплоту, переносимую конвекцией, а знаменатель — теплоту, переносимую теплопроводностью.

4. Безразмерный комплекс

называют числом Грасгофа. Оно характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей.

Используя введенные обозначения, систему безразмерных дифференциальных уравнений можно записать в следующем виде:

Безразмерные величины Θ,W_x, W_y, X, У, Nu, Re, Ре, Gr можно рассматривать как новые переменные.

Их можно разделить на три группы:

– независимые переменные — это безразмерные координаты X, У;

– зависимые переменные — это Nu, Θ, W_x, W_y ; они однозначно определяются значениями независимых переменных при определенных значениях величин, входящих в условия однозначности;

– постоянные величины — это Ре, Re, Gr; они заданы условиями однозначности и для конкретной задачи являются постоянными. Действительно, числа Ре, Re и Gr состоят только из величин, входящих в условия задачи.

В результате можно написать

Уравнения (3.4) называют уравнениями подобия.

Здесь Х_с , У_с соответствуют поверхности теплоотдачи (стенки). Нахождение а (или Nu) для точек пространства, не лежащих на поверхности стенки, не имеет смысла. В рассматриваемой задаче У_с = 0.

Если в уравнении движения учесть член-

то в результате приведения к безразмерной записи появился бы и член

5. Безразмерный комплекс

называют числомЭйлера.Эточисло характеризует соотношение сил давления и сил инерции.

Необходимо отметить, что при неизменной формулировке задачи новые безразмерные величины могут быть получены соответствующим комбинированием старых безразмерных комплексов, однако при этом число переменных под знаком функции не должно измениться.

Числу Прандтля можно придать определенный физический смысл.

и уравнение движения

При a = v расчетные поля температур и скоростей будут подобны, если только аналогичны и условия однозначности. Условию a = v соответствует равенствоРг = 1. Таким образом, при определенных условиях числу Прандтля может быть придан смысл меры подобия полей температур и скоростей.

В зависимости от значения числаРг жидкости делят на три группы: жидкости с числами Рг 1 (неметаллические капельные жидкости).

Учитывая, чтоPe=Re·Pr, уравнения подобия можно записать в виде:

Исходя из уравнений (3.5), безразмерные переменные можно разделить на два вида:

– определяемые — что числа, в которые входят искомые зависимые переменные; в рассматриваемом случае зависимыми являются a, θ,:w_x и w_y, следовательно, определяемыми будут Nu, θ, W_x и W_y;

– определяющие — это числа, целиком составленные из независимых переменных и постоянных величин, входящих в условия однозначности; в рассматриваемом случае определяющими являются X, У, Re, Рг (или Ре) и Gr.

Анализ размерностей и нормализация уравнений взаимосвязи физических величин.

Основной метод теории подобия – анализ размерностей физических величин, характеризующих состояние объекта исследования, и параметров, которые определяют это состояние. Под размерностью физической величины понимают выражение связи между ней и физическими величинами, положенными в основу системы единиц. Анализ размерностей позволяет определять вид таких уравнений взаимосвязи физических величин в изучаемых явлениях. Базой анализа размерностей служит требование, согласно которому основные уравнения, выражающие связь между переменными и параметрами объекта, должны быть справедливы при любом выборе единиц измерения входящих в них величин; значения переменных определяются решением данной системы уравнений, значения параметров должны быть заданы для решения этой системы. Из этого требования следует, в общем, что все слагаемые каждого уравнения должны иметь одинаковые размерности и, в частности, что с помощью операции, называемой нормализацией (преобразованием), могут быть приведены к безразмерному виду.

Нормализацию обычно проводят в два этапа. На первом этапе все переменные преобразуются к безразмерному виду путем выбора соответствующих масштабов так, чтобы диапазоны изменения всех безразмерных переменных были одинаковы (например, равны 1). При этом масштабные коэффициенты переменных включают в состав коэффициентов соответствующих членов нормализуемого уравнения. На втором этапе все члены уравнения делят на один из коэффициентов, что дает возможность сделать каждый член уравнения безразмерным. Если уравнение имеет начальные и граничные условия, то и они, соответственно, преобразуются.

Нормализованные уравнения содержат, как правило, величины двух типов:

а) безразмерные зависимые и независимые переменные;

б) безразмерные параметры (иногда называют π-комплексами).

Последние включают характерные размеры (масштабы) объекта, а также физические параметры исходного уравнения и граничных условий. Объекты, описание свойств которых сводится к одинаковым безразмерным уравнениям и граничным условиям, независимо от их физической природы относятся к одному классу. Очевидно, что геометрически подобные или даже физически идентичные системы нельзя относить к одному классу, если граничные условия для них не будут представлены одинаково (например, при различных профилях скоростей потока на входе в идентичные аппараты).

Объекты, относящиеся к одному классу и имеющие одинаковые численные значения π-комплексов в уравнениях и соответствующих граничных условиях, подобны, поскольку поля изменения физических характеристик, определяемые безразмерными переменными, отличаются лишь выбранными масштабными коэффициентов, отношения которых задают коэффициентами подобия. Поэтому π-комплексы называют также критериями или числами подобия, равенство которых для объектов, описываемых идентичными безразмерными уравнениями и граничными условиями, обеспечивает их подобие.

Изменение значений критериев подобия означает переход от одного объекта к другому в пределах объектов данного класса. При таком переходе условия подобия не соблюдаются, только при относительно небольших изменениях критериев или изменениях тех из них, которые слабо влияют на решение уравнений, можно говорить о неполном, или частичном, подобии. Такие случаи чаще всего встречаются на практике при изучении подобия реальных объектов. Например, при изменении геометрических размеров технологической установки затрудняется соблюдение постоянства критериев подобия, включающих объемные и поверхностные характеристики аппаратов, т. к. отношение объема к поверхности изменяется пропорционально их размерам.

Размерные физические параметры, входящие в критерии подобия, для подобных объектов могут иметь сильно различающиеся значения; важно только, чтобы мало отличались друг от друга значения самих критериев. Именно это свойство подобных систем составляет основу метода моделирования и позволяет корректно решать задачи масштабирования, т. е. использовать результаты исследований одного объекта при изучении другого, полностью или частично ему подобного, хотя и существенно отличающегося размерами либо режимами работы. Поэтому соблюдение постоянства критериев подобия – решающее условие успешного переноса исследований на иные объекты.

3.10.3. Анализ решения нормализованных уравнений

Важное следствие процедуры нормализации состоит в том, что число критериев подобия в безразмерных уравнениях и их граничных условиях всегда оказывается меньше числа физических параметров, входящих в исходные соотношения. С одной стороны, это устанавливает необходимое количество критериев подобия различных объектов, принадлежащих к одному классу, с другой – упрощает до некоторой степени решение целого ряда сложных задач.

Решения безразмерных уравнений с соответствующими граничными условиями определяют безразмерные переменные объекта как функции независимых переменных и критериев:

(3.80)

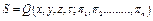
где х, у, z — безразмерные пространств. координаты; τ — безразмерная переменная, соответствующая времени; π₁—π_n-критерии подобия.

Безразмерный вид функции Q зависит от вида уравнений и граничных условий и обычно не может быть записан в общей форме. Однако сам факт существования зависимости (3.80) приводит к различным выводам. Например, при решении задачи оценки некоторых параметров начальных уравнений по опытным данным выражение (3.80) позволяет установить, какими критериями определяется безразмерный комплекс, включающий неизвестный параметр. Далее можно попытаться найти данную связь в виде некоторой принятой (например, степенной) функциональной зависимости от остальных критериев. Для этого выполняют необходимый объем экспериментов в различных условиях (при которых изменяются значения критериев) и с помощью выбранной зависимости осуществляют соответствующие расчеты наблюдаемых результатов. Полученное соотношение может быть использовано уже для анализа целой группы объектов, критерии подобия которой отвечают изученной области изменения их значений. Такие исследования часто проводят при решении проблем гидромеханики, тепло- и массообмена и т. п. в химико-технологических процессах.

Дата добавления: 2015-01-29 ; просмотров: 2082 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Условия подобия физических процессов.

ОСНОВЫ ТЕОРИИ ПОДОБИЯ.

Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. Попытки аналитического решения полной системы уравнений наталкиваются на серьезные трудности. Поэтому большое значение приобретает экспериментальный путь исследования. С помощью эксперимента для определенных значений аргументов можно получить числовые значения искомых переменных и затем подобрать уравнения, описывающие результаты опытов. Однако при изучении столь сложного процесса, как конвективный теплообмен, не всегда легко проводить и опытное исследование.

Для исследования влияния на процесс какой – либо величины остальные нужно сохранять неизменными, что не всегда возможно или затруднительно из-за большого количества переменных. Кроме того, при этом нужно быть уверенными, что результаты, получаемые с помощью какой-либо конкретной установки (модели ), можно перенести на другие аналогичные процессы (образец). Эти трудности помогает разрешить теория подобия. С помощью теории подобия размерные физические величины можно объединить в безразмерные комплексы, причем так, что комплексов будет меньше числа величин, из которых составлены эти комплексы. Полученные безразмерные комплексы можно рассматривать как новые переменные.

При введении в уравнения безразмерных комплексов число величин под знаком искомой функции формально сокращается, что упрощает исследование физических процессов. Кроме того, новые безразмерные переменные отражают влияние не только отдельных факторов, но их совокупности, что позволяет легче определить физические связи в исследуемом процессе.

Теория подобия устанавливает также условия, при которых результаты лабораторных исследований можно распространить на другие явления, подобные рассматриваемому.

Для практического исследования выводов теории подобия необходимо уметь приводить к безразмерному виду математические описания изучаемых процессов.

Имеется несколько методов выполнения этой операции.

Один из них — метод масштабных преобразований.

; ; ; .

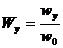
В результате масштабирования получим новые безразмерные переменные:

Помимо приведенных безразмерных величин в уравнение входят безразмерные комплексы, состоящие из различных физических величин. Эти комплексы называются числами подобия.

Первый из этих безразмерных комплексов обозначают:

1) — число Нуссельта,

где — коэффициент теплоотдачи, ;

— коэффициент теплопроводности жидкости, ;

— характеристический размер, м.

Число Нуссельта характеризует конвективный теплообмен между жидкостью и поверхностью твердого тела. Число Нуссельта еще называют безразмерным коэффициентом теплоотдачи.

Несмотря на внешнее сходство с числом Био, рассмотренном при изучении теплопроводности, число Нуссельта существенно отличается от него. В число Bi входит коэффициент теплопроводности твердого тела; в число Nu-коэффициент теплопроводности жидкости. Кроме того, в число Био коэффициент теплоотдачи вводиться как величина, заданная в условиях однозначности, а мы рассматриваем коэффициент теплоотдачи, входящий в Nu, как величину искомую.

2) — число Рейнольдса,

где — скорость движения жидкости, м/с;

— коэффициент кинематической вязкости жидкости, .

Число Рейнольдса характеризует течение жидкости и представляет собой отношение сил инерции к силам вязкости.

Число Рейнольдса является важной характеристикой, как в изотермических, так и в неизотермических процессов течения жидкости.

Третий безразмерный комплекс обозначают:

3) — Число Пекле,

где — число Прандтля.

Число Пекле характеризует собой отношение теплоты, переносимой конвекцией к теплоте, переносимой теплопроводностью.

Число Прандтля характеризует физические свойства жидкости и является мерой подобия полей температур и скоростей.

,

где – коэффициент температуропроводности жидкости, .

Для капельных жидкостей число изменяется от температуры аналогично вязкости:

,

То есть при повышении температуры число Прандтля и вязкость уменьшаются.

Для газов число практически не зависит от температуры и давления и является для данного газа величиной постоянной и определяемой атомностью газа:

— для одноатомных газов число = 0,67

— для двухатомных газов число = 0,72

— для трехатомных газов число = 0,80

— для четырехатомных и более число = 1

Для тяжелых и щелочных жидких металлов число Прандтля = 0,005 0,05.

Малые значения числа Pr жидких металлов объясняется высокой теплопроводностью последних.

4) — Число Грасгофа,

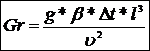
где — коэффициент объемного расширения;

— разность температуры между стенкой и жидкостью.

Оно характеризует соотношение подъемной силы, возникающей в результате разности плотностей жидкости к силам молекулярного трения.

5) — Число Архимеда,

где и — плотности нагретой и холодной жидкости,

Число Архимеда представляет собой модификацию числа Грасгофа. Если =const, .

Уравнения подобия

Полученные безразмерные комплексы можно рассматривать как новые переменные. Их можно разбить на 3 группы:

1. независимые переменные: X, Y

2. зависимые:

3. постоянные величины (они состоят из условий однозначности): .

Кроме того безразмерные переменные можно разделить на две большие группы:

1.Определяемые величины-это числа, в которые входят искомые зависимые ,

следовательно, определяемыми являются

2.Определяющие величины — это числа, целиком составленные из независимых переменных и постоянных величин, входящих в условия однозначности: X,Y,Re,Pr,Pe и Gr.

Уравнением подобия называется зависимость между каким-либо определяемым числом подобия и другими определяющими числами.

Условия подобия физических процессов.

Выражаются тремя теоремами подобия:

Первая теорема подобия (теорема Ньютона) – подобные процессы должны быть качественно одинаковыми, то есть они должны иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями, а также иметь одинаковые числа подобия, т.е.:

Вторая теорема подобия (теорема Бэкингема) – зависимость между переменными, характеризующими какой-либо процесс может быть представлен в виде уравнения подобия. Уравнения подобия для подобных между собой процессов одинаковы. Зависимости между физическими параметрами, характеризующими какое либо явление, могут быть представлены методами масштабных преобразований, анализа размерностей или др.

Третья теорема подобия (теорема Кирпичева и Гухмана). Необходимым условием и достаточным условием подобия физических явлений является подобие условий однозначности (заданных условий) при равенстве чисел подобия , составленных из условий однозначности. Более конкретно смысл третьей теоремы подобия формулируется так.

1.Подобные явления происходят в геометрически подобных системах и описываются подобными уравнениями.

2.Для теплового подобия необходимо наличие физического подобия движения жидкостей.

3.При указанных условиях подобны те явления, для которых подобны условия однозначности, а числа подобия, составленные из условий однозначности, численно равны.

Необходимой предпосылкой теории подобия является математическое описание изучаемого процесса в виде дифференциальных уравнений и условий однозначности.