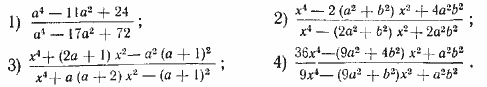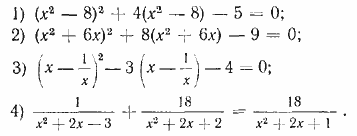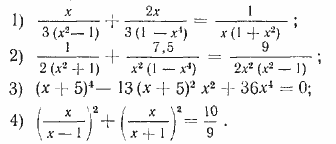Биквадратные уравнения примеры для решения с ответами

Биквадратные уравнения

Биквадратное уравнение — уравнение, которое можно привести к виду:

Для решения биквадратных уравнений x 2 заменяется на любую другую букву, например, на y, то есть:

Следовательно, относительно y, уравнение является квадратным и решается по формуле корней квадратного уравнения, а затем вычисляются корни биквадратного уравнения, если они есть.

Пример. Решить уравнение:

Решение: Заменяем x 2 на y, чтобы получить квадратное уравнение:

D = b 2 — 4ac = (-10) 2 — 4 · 1 · 9 = 100 — 36 = 64, D > 0.

Биквадратные уравнения примеры для решения с ответами

3 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КВАДРАТНЫЕ УРАВНЕНИЯ

§ 8. БИКВАДРАТНЫЕ УРАВНЕНИЯ

Решить биквадратные уравнения:

458. 1) х 4 + х 2 — 2 = 0;
2) х 4 — 3х 2 — 4 = 0;
3) 9х 4 + 8х 2 — 1 = 0;
4) 20х 4 — х 2 — 1 = 0.

459. 1) х 4 — 26х 2 + 25 = 0;
2) х 4 — 40х 2 + 144 = 0;
3) 4х 4 — 5х 2 + 1 = 0;
4) 4х 4 — 17х 2 + 4 = 0.

460. 1) х 4 — 18х 2 + 81=0;
2) 256х 4 — 32х 2 +1=0;
3) х 4 — 8х 2 + 20 = 0;
4) 5х 4 — 4х 2 + 1 = 0.

462. Убедиться, что уравнение х 4 + 10х 2 + 9 = 0 не имеет действительных корней. Почему этот вывод можно сделать, не решая уравнения?

463. Дано биквадратное уравнение ах 4 + bх 2 + с = 0, где а, b, с—данные действительные числа, причем а > 0. Введя вспомогательное неизвестное у = х 2 , исследовать корни данного уравнения и результаты исследования занести в таблицу 4.

464. Решить уравнения:

465. Почему биквадратное уравнение, имеющее корень, равный т, имеет также и второй корень, равный — т?

466. Один из корней биквадратного уравнения равен 2, а другой корень 2√ 2 . Составить уравнение.

* 467. Составить биквадратное уравнение, сумма квадратов корней которого равна 26, а произведение корней равно 36.

468. Разложить на множители:

469. Сократить дроби:

470. Решить уравнения посредством введения вспомогательного неизвестного:

471. Решить уравнения выделением из левой части полного квадрата:

1) х 4 — 20х 2 + 64 = 0;
2) х 4 — 13х 2 + 36 = 0;
3) х 4 — 4х 2 + 1 = 0;
4) х 4 — 2х 2 +1 = 0.

472*. Зная, что т и п— корни уравнения х 2 + рх + q = 0, найти биквадратное уравнение, имеющее корни —т, —п, т и п.

473. Решить уравнения:

474*. В какой системе счисления число 100 запишется в виде 10 201?

475. Сумма площадей двух квадратов равна 4,25 дм 2 . Найти коэффициенты подобия этих квадратов, если известно, что их стороны выражаются взаимно обратными числами.

476. Каким радиусом следует описать дугу с центром на окружности, радиус которой R, чтобы расстояние между точками пересечения этой дуги с данной окружностью было равно а, где а 3 ; R√ 2 и R.

Биквадратные уравнения

теория по математике 📈 уравнения

Уравнение вида ax 4 +bx 2 +c=0, где а≠0 число, называется биквадратным уравнением (приставка «би» означает «двойной»). Для решения такого уравнения применяют метод введения новой переменной, чтобы получить квадратное уравнение, решение которого легко выполняется.

Рассмотрим на примерах решение таких уравнений.

Пример №1. Решить уравнение:

В данном уравнении заменим х 2 на переменную, например а (букву для замены можно брать любую): х 2 =а. Степень данного уравнения при этом понизится на 2, получаем квадратное уравнение:

Решаем данное уравнение, например, по теореме Виета. Тогда:

Методом подбора получаем корни квадратного уравнения 9 и 16. Проверяем, что действительно 9+16=25, 916=144. Теперь переходим к нахождению корней биквадратного уравнения, которое дано по условию. Мы заменяли х 2 на а, поэтому подставляем вместо а полученные значения – это 9 и 16:

Теперь находим корни каждого из этих неполных квадратных уравнений: х 2 =9, отсюда уравнение имеет два корня ±3; х 2 =16, отсюда имеет еще два корня ±4. Следовательно, данное биквадратное уравнение имеет четыре корня: 3, -3, 4, -4.

Пример №2. Решить уравнение:

Заменим на переменную у: х 2 =у. Получим уравнение:

Найдем его корни: у₁=–1, у₂=4. Подставим корни вместо у и получим уравнения: х 2 =–1; х 2 =4. Видим, что первое неполное квадратное уравнение не имеет корней, а корни второго уравнения – это ±2. Значит, данное биквадратное уравнение имеет корни ±2.

Пример №3. Решить уравнение:

Выполним замену переменной: х 2 =у. Решим уравнение:

Подбором корни найти невозможно, поэтому через дискриминант получаем, что корней нет, так как дискриминант будет отрицательный. Значит и данное биквадратное уравнение тоже не имеет корней.