Основные блок-схемы решения линейных и квадратичных задач с параметрами
Разделы: Математика
Задачи с параметрами (ЗсП) традиционно являются наиболее сложными для учащихся, поскольку требуют от них умения логически рассуждать и проводить анализ решения. Подобные задачи являются первыми исследовательскими задачами, с которыми встречаются школьники. Для их решения не требуются знания, выходящие за пределы школьной программы, но недостаточно применения лишь стандартных приемов, а необходимо глубокое понимание всех разделов элементарной математики.
В данной статье предпринята попытка систематизации и формализации (в форме блок-схем) наиболее часто встречающихся и наиболее типичных ЗсП. При этом выделены классы задач, решаемых по единой методике.
Рассматриваются аналитические методы решения ЗсП, сводящиеся к исследованию линейных или квадратных уравнений (неравенств), а также квадратного трехчлена. Такой выбор обусловлен тем, что курс школьной математики ограничен «вглубь», по существу, «теорией квадратичного».
Линейные уравнения
Определение. Уравнение вида ax=b, где a, b принадлежат множеству всех действительных чисел, будем называть стандартным видом линейного уравнения. Всевозможные варианты, возникающие при решении линейных уравнений, отразим в блок–схеме I.
Количество корней линейного уравнения отразим в блок-схеме II:
Пример 1. Для всех действительных значений параметра m решите уравнение m 2 x–2=4x+m.
Решение. Приведем заданное линейное уравнение к стандартному виду:
m 2 x–2=4x+m, m 2 x–4x=m+2, (m 2 –4)x=m+2.(1)
Следуя схеме I, рассмотрим два случая для коэффициента при x:
1)если m 2 – 4 не равно 0, m не равно ±2, то x=(m+2)/(m 2 -4), x=1/(m–2);
а) при m = –2 уравнение (1) примет вид 0х=0, отсюда х – любое действительное число;
б) при m = 2 уравнение (1) примет вид 0х= 4, отсюда следует, что корней нет.
Ответ. Если m 2 то x=1/(m–2); если m= – 2, то x – любое действительное число; если m=2, то корней нет.
Пример 2. При каких значениях параметра k уравнение 2(k–2x)=kx+3 не имеет корней?
Решение. 2(k–2x)=kx+3, (k+4)x=2k–3. В силу схемы II уравнение не имеет корней, если k+4=0 и 2k–3 не равно 0 => k= –4 и k не равно 1,5 => k = –4.
Ответ. k=–4.
Системы линейных уравнений
Определение 1. Система называется совместной, если она имеет хотя бы одно решение.
Определение 2. Система называется несовместной, если она не имеет ни одного решения.
Количество решений системы линейных уравнений отразим в блок-схеме III.
Замечание. Так как уравнение прямой y=kx+b в общем виде записывается следующим образом ax+by+c=0, то взаимное расположение двух прямых отразим в блок-схеме IV.
Пример. При каких значениях параметра c система из двух уравнений c 2 x+(2–c)y–4=c3 и (2c–1)y+cx+2=c 5 совместна?
Решение. Запишем систему в стандартном виде: c 2 x+(2–c)y=c 3 +4 и cx+(2c–1)y=c 5 –2. Сначала найдем значения c, при которых эта система не имеет решений. В силу схемы III имеем условие,
c 2 /с=(2-с)/(2с–1), с не равно (c 3 +4)/(c 5 –2),
которое равносильно системе из уравнения и неравенства
с=(2–с)/(2с–1) и с не равно (c 3 +4)/(c 5 –2).
Решением системы является с=1. Итак, система имеет решения при всех действительных значениях с, кроме с=1.
Ответ. с — любое действительное число, с не равно 1.
Линейные неравенства
Определение. Неравенство вида ax>b, ax b, ax b, отразим в блок-схеме V.
Пример. Для всех значений параметра m решите неравенство 5x–m>mx–3.
Решение. 5x–m>mx–3, (5–m)x>m–3.
Следуя схеме V, рассмотрим три случая для коэффициента при х:
2)если 5–m 5, то x 2. Откуда следует, что решений нет.
Ответ. Если m (m–3)/(5–m); если m=5, то решений нет; если m>5, то х 2 +bx+c=0, где a, b, c — любые действительные числа, a>0, называется квадратным уравнением относительно действительного переменного x.
Ситуации, возникающие при решении квадратных уравнений, отразим в блок–схеме VI.
Пример. При каких значениях параметра c уравнение (c–2)x 2 +2(с–2)x+2=0 не имеет корней?
Решение. Рассмотрим два случая:
1) если с–2 не равно 0, c не равно 2, то D 2 –2(c–2) 2 +(c+4)x+c+7=0 имеет только отрицательные корни?
Решение. В силу условия задачи необходимо рассмотреть два случая (линейный и квадратичный):
1) если c–1=0, c=1, то уравнение примет вид 5x+8=0, x= –5/8 – отрицательный корень;
2) если c–1 не равно 0, c не равно 1, то, следуя схеме VII, получим систему
Решением ее являются промежутки –22/3 2 +bx+c, где a не равно 0, называется квадратичной. График квадратичной функции называется параболой.
Абсциссы точек пересечения параболы y=ax 2 +bx+c с осью (Ox) являются корнями уравнения ax 2 +bx+c=0.
Учитывая это, отразим взаимное расположение параболы и оси (Ox) в следующей схеме:
Замечание. Если уравнение параболы имеет вид y=a(x–p) 2 +q, то (p; q) – координаты вершины параболы.
Пример 1. При каких значениях параметра a вершина параболы y=(x–7a) 2 +a 2 –10+3a лежит в III координатной четверти?
Решение. Пусть (x0, y0) – координаты вершины параболы. В силу замечания имеем x0=7a, y0=a 2 –10+3a. Так как вершина параболы лежит в третьей четверти, то
Ответ. –5
Пример 2. При каких значениях параметра b график функции y=(4–b 2 )x 2 +2(b+2)x–1 лежит ниже оси (Ox)?
Решение. Рассмотрим два случая.
1. Пусть 4–b 2 =0, b= + 2;
1) если b=2, то прямая y=8x–1 не лежит ниже оси (Ox);
2) если b= –2, то прямая y= –1 лежит ниже оси (Ox).
2. Пусть 4–b 2 не равно 0. Тогда в соответствии со схемой VIII получим
Объединяя ответы, получим b 2 +bx+c=0. Введем функцию y(x)= ax 2 +bx+c. Тогда расположение корней этого уравнения на числовой оси отразим в блок–схеме IX.
Следствие. С учетом схемы IX схема VII для знаков корней квадратного уравнения примет следующий вид:
Пример. При каких значениях параметра a корни уравнения x 2 –2(a+3)x+a 2 +6,25a+8=0 больше 2?
Решение. Введем функцию y(x)=x 2 –2(a+3)x+a 2 +6,25a+8; x0 – абсцисса вершины этой параболы. Так как корни уравнения находятся справа от числа 2, то в соответствии со схемой IX имеем:
Решение. Данная задача равносильна следующей: при каких значениях параметра b система
имеет одно решение?
Решим неравенство (2): 2x 2 –2x–1>0, x1,2=0,5(1±(3) 1/2 ), x 1/2 ) или x>0,5(1+(3) 1/2 ).
Найдем корни уравнения (1): D=(2b–7) 2 , x1=2, x2=2b–5. Поскольку корень x1=2 удовлетворяет неравенству (2), то система имеет одно решение в следующих случаях:
1) если x2=2b–5 не удовлетворяет неравенству (2), то 0,5(1–(3) 1/2 ) 1/2 ) или 0,25(11–O3) 1/2 );
Ответ. 0,25(11–(3) 1/2 ) 1/2 ), b=3,5.
Пример 2. При каких значениях параметра p уравнение 5–4sin 2 x–8cos 2 (x/2)=3p имеет корни?
Решение. Преобразуем заданное уравнение:
5– 4sin 2 x–8cos 2 (x/2)=3p => 5–4(1–cos2x)–4(1+cosx)=3p => 4cos 2 x–4cosx–3p–3=0.
Сделаем замену cosx=t. Тогда заданная задача равносильна следующей: при каких значениях p система
4t2–4t–3p–3=0, (1)
-1 2 –4t–3p–3; t0–вершина этой параболы. В силу схемы IX случаи 1, 2 и 3 описываются следующей совокупностью:
Блок схема алгоритма системы решения линейных уравнений
Блок 1. Линейные уравнения и неравенства с параметрами
Покажем решение линейного уравнения 
SHAPE \* MERGEFORMAT
Рис.1. Блок-схема решения линейного уравнения.
Эта блок-схема удобна тем, что идеально отражает обычное для задач с параметрами «ветвление» решения в зависимости от значений параметра. Мы видим, что из одного уравнения 



Добавим, что в рассмотренной блок-схеме предполагается, что все значения и переменной x , и параметра a являются допустимыми. Если это не так, т.е. при определенных значениях x и a уравнение не имеет смысла, то решение усложняется. Возникает необходимость во-первых, определить эти недопустимые значения, а во-вторых, учесть их в процессе решения.
Часто в задачах на линейные уравнения и неравенства с параметрами бывает полезно «опереться» на линейную функцию 
SHAPE \* MERGEFORMAT
Рис.2. График линейной функции.
Это, как известно, прямая, расположенная под углом 



В этом же модуле рассмотрим тему «Системы двух линейных уравнений с двумя неизвестными с параметрами».
Решить такую систему – значит найти такие пары чисел 

Учитывая тот факт, что каждое уравнение системы геометрически представляет прямую на плоскости, возможны три случая расположения двух прямых, а, следовательно, три случая решения системы.
Метод Гаусса решения системы линейных уравнений
Дана система 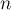
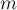
Формально задача ставится следующим образом: решить систему:
где коэффициенты 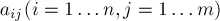

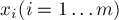
Удобно матричное представление этой задачи:
где 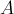
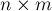
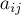
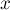
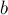
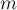
Стоит отметить, что СЛАУ может быть не над полем действительных чисел, а над полем по модулю какого-либо числа 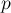
— алгоритм Гаусса работает и для таких систем тоже (но этот случай будет рассмотрен ниже в отдельном разделе).
Алгоритм Гаусса
Строго говоря, описываемый ниже метод правильно называть методом «Гаусса-Жордана» (Gauss-Jordan elimination), поскольку он является вариацией метода Гаусса, описанной геодезистом Вильгельмом Жорданом в 1887 г. (стоит отметить, что Вильгельм Жордан не является автором ни теоремы Жордана о кривых, ни жордановой алгебры — всё это три разных учёных-однофамильца; кроме того, по всей видимости, более правильной является транскрипция «Йордан», но написание «Жордан» уже закрепилось в русской литературе). Также интересно заметить, что одновременно с Жорданом (а по некоторым данным даже раньше него) этот алгоритм придумал Класен (B.-I. Clasen).
Базовая схема
Кратко говоря, алгоритм заключается в последовательном исключении переменных из каждого уравнения до тех пор, пока в каждом уравнении не останется только по одной переменной. Если 
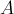
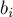
При этом алгоритм основывается на двух простых эквивалентных преобразованиях системы: во-первых, можно обменивать два уравнения, а во-вторых, любое уравнение можно заменить линейной комбинацией этой строки (с ненулевым коэффициентом) и других строк (с произвольными коэффициентами).
На первом шаге алгоритм Гаусса-Жордана делит первую строку на коэффициент 

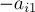
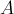
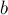
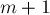
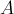
В итоге, по окончании первого шага первый столбец матрицы 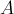
Аналогично производится второй шаг алгоритма, только теперь рассматривается второй столбец и вторая строка: сначала вторая строка делится на 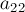
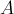
И так далее, пока мы не обработаем все строки или все столбцы матрицы 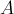

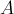
Поиск опорного элемента (pivoting)
Разумеется, описанная выше схема неполна. Она работает только в том случае, если на каждом 


Чтобы сделать алгоритм работающим в таких случаях, как раз и существует процесс выбора опорного элемента (на английском языке это называется одним словом «pivoting»). Он заключается в том, что производится перестановка строк и/или столбцов матрицы, чтобы в нужном элементе 
Заметим, что перестановка строк значительно проще реализуется на компьютере, чем перестановка столбцов: ведь при обмене местами двух каких-то столбцов надо запомнить, что эти две переменных обменялись местами, чтобы затем, при восстановлении ответа, правильно восстановить, какой ответ к какой переменной относится. При перестановке строк никаких таких дополнительных действий производить не надо.
К счастью, для корректности метода достаточно одних только обменов строк (т.н. «partial pivoting», в отличие от «full pivoting», когда обмениваются и строки, и столбцы). Но какую же именно строку следует выбирать для обмена? И правда ли, что поиск опорного элемента надо делать только тогда, когда текущий элемент 
Общего ответа на этот вопрос не существует. Есть разнообразные эвристики, однако самой эффективной из них (по соотношению простоты и отдачи) является такая эвристика: в качестве опорного элемента следует брать наибольший по модулю элемент, причём производить поиск опорного элемента и обмен с ним надо всегда, а не только когда это необходимо (т.е. не только тогда, когда 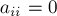
Иными словами, перед выполнением 


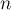

Во-первых, эта эвристика позволит решить СЛАУ, даже если по ходу решения будет случаться так, что элемент 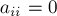
Без этой эвристики, даже если система такова, что на каждой 


Вырожденные случаи
Итак, если останавливаться на алгоритме Гаусса-Жордана с partial pivoting, то, утверждается, если 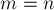
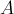
Рассмотрим теперь общий случай — когда 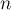
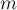





Итак, некоторые переменные в процессе работы алгоритма могут оказываться независимыми. Понятно, что когда количество 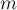
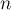
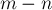
В целом, если обнаружилась хотя бы одна независимая переменная, то она может принимать произвольное значение, в то время как остальные (зависимые) переменные будут выражаться через неё. Это означает, что, когда мы работаем в поле действительных чисел, система потенциально имеет бесконечно много решений (если мы рассматриваем СЛАУ по модулю, то число решений будет равно этому модулю в степени количества независимых переменных). Впрочем, следует быть аккуратным: надо помнить о том, что даже если были обнаружены независимые переменные, тем не менее СЛАУ может не иметь решений вовсе. Это происходит, когда в оставшихся необработанными уравнениях (тех, до которых алгоритм Гаусса-Жордана не дошёл, т.е. это уравнения, в которых остались только независимые переменные) есть хотя бы один ненулевой свободный член.
Впрочем, проще это проверить явной подстановкой найденного решения: всем независимыми переменным присвоить нулевые значения, зависимым переменным присвоить найденные значения, и подставить это решение в текущую СЛАУ.
Реализация
Приведём здесь реализацию алгоритма Гаусса-Жордана с эвристикой partial pivoting (выбором опорного элемента как максимума по столбцу).
На вход функции 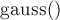
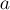
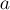
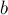
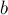
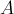
Функция возвращает число решений системы (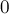

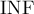
В функции поддерживаются два указателя — на текущий столбец 
Также заводится вектор 
Реализация использует технику partial pivoting, производя поиск строки с максимальным по модулю элементом, и переставляя затем эту строку в позицию 
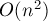
В реализации в целях простоты текущая строка не делится на опорный элемент — так что в итоге по окончании работы алгоритма матрица становится не единичной, а диагональной (впрочем, по-видимому, деление строки на ведущий элемент позволяет несколько уменьшить возникающие погрешности).
После нахождения решения оно подставляется обратно в матрицу — чтобы проверить, имеет ли система хотя бы одно решение или нет. Если проверка найденного решения прошла успешно, то функция возвращает 
Асимптотика
Оценим асимптотику полученного алгоритма. Алгоритм состоит из 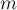
- поиск и перестановка опорного элемента — за время
при использовании эвристики «partial pivoting» (поиск максимума в столбце)
- если опорный элемент в текущем столбце был найден — то прибавление текущего уравнения ко всем остальным уравнениям — за время
Очевидно, первый пункт имеет меньшую асимптотику, чем второй. Заметим также, что второй пункт выполняется не более 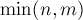
Таким образом, итоговая асимптотика алгоритма принимает вид 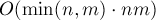
При 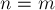

Заметим, что когда СЛАУ рассматривается не в поле действительных чисел, а в поле по модулю два, то систему можно решать гораздо быстрее — об этом см. ниже в разделе «Решение СЛАУ по модулю».
Более точная оценка числа действий
Для простоты выкладок будем считать, что 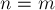
Как мы уже знаем, время работы всего алгоритма фактически определяется временем, затрачиваемым на исключение текущего уравнения из остальных.
Это может происходить на каждом из 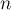
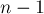
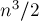
Дополнения
Ускорение алгоритма: разделение его на прямой и обратный ход
Добиться двукратного ускорения алгоритма можно, рассмотрев другую его версию, более классическую, когда алгоритм разбивается на фазы прямого и обратного хода.
В целом, в отличие от описанного выше алгоритма, можно приводить матрицу не к диагональному виду, а к треугольному виду — когда все элементы строго ниже главной диагонали равны нулю.
Система с треугольной матрицей решается тривиально — сначала из последнего уравнения сразу находится значение последней переменной, затем найденное значение подставляется в предпоследнее уравнение и находится значение предпоследней переменной, и так далее. Этот процесс и называется обратным ходом алгоритма Гаусса.
Прямой ход алгоритма Гаусса — это алгоритм, аналогичный описанному выше алгоритму Гаусса-Жордана, за одним исключением: текущая переменная исключается не из всех уравнений, а только из уравнений после текущего. В результате этого действительно получается не диагональная, а треугольная матрица.
Разница в том, что прямой ход работает быстрее алгоритма Гаусса-Жордана — поскольку в среднем он делает в два раза меньше прибавлений одного уравнения к другому. Обратный ход работает за 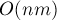
Таким образом, если 
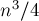
Решение СЛАУ по модулю
Для решения СЛАУ по модулю можно применять описанный выше алгоритм, он сохраняет свою корректность.
Разумеется, теперь становится ненужным использовать какие-то хитрые техники выбора опорного элемента — достаточно найти любой ненулевой элемент в текущем столбце.
Если модуль простой, то никаких сложностей вообще не возникает — происходящие по ходу работы алгоритма Гаусса деления не создают особых проблем.
Особенно замечателен модуль, равный двум: для него все операции с матрицей можно производить очень эффективно. Например, отнимание одной строки от другой по модулю два — это на самом деле их симметрическая разность («xor»). Таким образом, весь алгоритм можно значительно ускорить, сжав всю матрицу в битовые маски и оперируя только ими. Приведём здесь новую реализацию основной части алгоритма Гаусса-Жордана, используя стандартный контейнер C++ «bitset»:
Как можно заметить, реализация стала даже немного короче, при том, что она значительно быстрее старой реализации — а именно, быстрее в 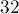
Если модуль произвольный (не обязательно простой), то всё становится несколько сложнее. Понятно, что пользуясь Китайской теоремой об остатках, мы сводим задачу с произвольным модулем только к модулям вида «степень простого». [ дальнейший текст был скрыт, т.к. это непроверенная информация — возможно, неправильный способ решения ]
Наконец, рассмотрим вопрос числа решений СЛАУ по модулю. Ответ на него достаточно прост: число решений равно 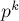
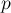
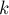
Немного о различных способах выбора опорного элемента
Как уже говорилось выше, однозначного ответа на этот вопрос нет.
Эвристика «partial pivoting», которая заключалась в поиске максимального элемента в текущем столбце, работает на практике весьма неплохо. Также оказывается, что она даёт практически тот же результат, что и «full pivoting» — когда опорный элемент ищется среди элементов целой подматрицы — начиная с текущей строки и с текущего столбца.
Но интересно отметить, что обе эти эвристики с поиском максимального элемента, фактически, очень зависят от того, насколько были промасштабированы исходные уравнения. Например, если одно из уравнений системы умножить на миллион, то это уравнение почти наверняка будет выбрано в качестве ведущего на первом же шаге. Это кажется достаточно странным, поэтому логичен переход к немного более сложной эвристике — так называемому «implicit pivoting».
Эвристика implicit pivoting заключается в том, что элементы различных строк сравниваются так, как если бы обе строки были пронормированы таким образом, что максимальный по модулю элемент в них был бы равен единице. Для реализации этой техники надо просто поддерживать текущий максимум в каждой строке (либо поддерживать каждую строку так, чтобы максимум в ней был равен единице по модулю, но это может привести к увеличению накапливаемой погрешности).
Улучшение найденного ответа
Поскольку, несмотря на различные эвристики, алгоритм Гаусса-Жордана всё равно может приводить к большим погрешностям на специальных матрицах даже размеров порядка 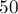
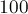
В связи с этим, полученный алгоритмом Гаусса-Жордана ответ можно улучшить, применив к нему какой-либо простой численный метод — например, метод простой итерации.
Таким образом, решение превращается в двухшаговое: сначала выполняется алгоритм Гаусса-Жордана, затем — какой-либо численный метод, принимающий в качестве начальных данных решение, полученное на первом шаге.
Такой приём позволяет несколько расширить множество задач, решаемых алгоритмом Гаусса-Жордана с приемлемой погрешностью.
http://files.school-collection.edu.ru/dlrstore/cf31a70f-4e2d-4c28-9db5-dfee83e8b6cb/block1.htm
http://e-maxx.ru/algo/linear_systems_gauss

















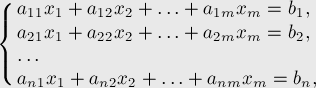
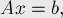
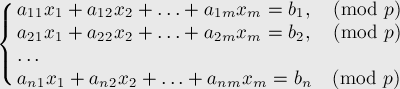
 при использовании эвристики «partial pivoting» (поиск максимума в столбце)
при использовании эвристики «partial pivoting» (поиск максимума в столбце)