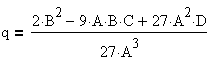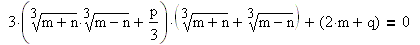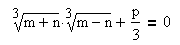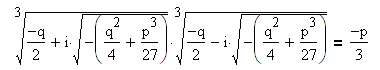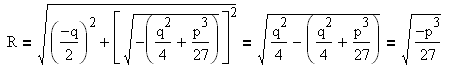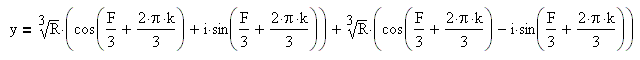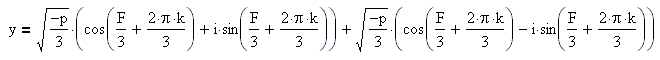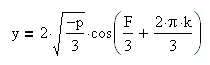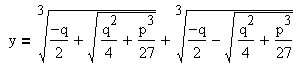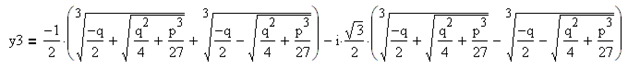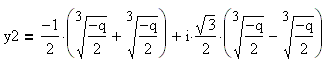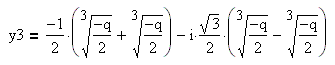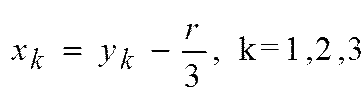Методы решения кубических уравнений
В области комплексных чисел, согласно основной теореме алгебры, кубическое уравнение всегда имеет 3 корня (с учётом кратности). Так как каждый вещественный многочлен нечётной степени имеет хотя бы один вещественный корень, все возможные случаи состава корней кубического уравнения исчерпывается тремя, которые легко различаются с помощью дискриминанта 
· Если Δ > 0, тогда уравнение имеет три различных вещественных корня.
· Если Δ = 0, тогда хотя бы два корня совпадают. Это может быть, когда уравнение имеет двойной вещественный корень и ещё один отличный от них вещественный корень; либо, все три корня совпадают, образуя корень кратности 3.
Корни кубического уравнения 

Исходя из основных свойств решения кубических уравнений, необходимо дать определение понятию «комплексное число». Комплексные числа — числа вида x + y , где x и y – вещественные числа, i – мнимая единица , то есть: i 2 = –1. Числа x = Â (z) ( или Re z ) и y = Á (z) ( или Im z ) называются соответственно вещественной и мнимой частями z . Множество всех комплексных чисел обозначается 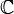
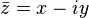
Наиболее распространенный метод решения кубических уравнений – метод перебора. [2] Сначала путём перебора находится один из корней уравнения (например, x 1 ). Вторая стадия решения – это деление многочлена ax 3 + bx 2 + cx + d на двучлен x – x 1 и решение полученного квадратного уравнения.
Алгоритм решения кубических уравнений с использованием формулы Кардано
В данном разделе статьи приведен подробный алгоритм решения уравнений третьей степени с помощи формулы Кардано. Данный алгоритм состоит из двух этапов. На первом этапе кубические уравнения приводятся к форме, в которой отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями. На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям . [3]
Рассмотрим алгоритм нахождения всех корней кубического уравнения 



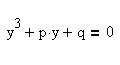
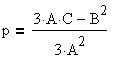
Дискриминантом уравнения 

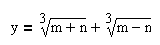
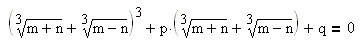
Число 
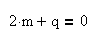
Находим числа m и n:
Дальнейшее решение зависит от знака дискриминанта S.
1. Пусть дискриминант меньше нуля. Тогда уравнение имеет три различных корня.
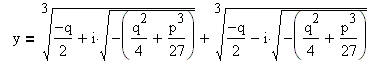
Найдём модуль комплексных чисел 
Аргумент числа 
· Если 
· Если 
· Если 
Для k=0, k=1, k=2 получаем решение:
Итак, если дискриминант меньше нуля, то уравнение имеет три различных действительных корня:
2. Пусть дискриминант больше нуля. Тогда уравнение имеет один действительный корень и два комплексно-сопряжённых.
При этом для любых комплексных значений корней необходимо выполнение условия: 
Примем аргумент F действительных чисел, стоящих под знаком кубического корня, равным нулю. При этом модули этих чисел могут принимать отрицательное значение. Аргумент кубического корня будет принимать 3 значения: 0, 2*π/3, 4*π/3. Каждое решение y=y1, y=y2, y=y3 будет состоять из суммы двух комплексных чисел 
Число z1 находится в группе из трёх чисел:
Число z2 находится в группе из трёх чисел:
Для действительных значений кубических корней выполняется обозначенное выше условие. Поэтому действительный корень уравнения 



Итак, если дискриминант больше нуля, то уравнение имеет один действительный корень и два комплексно-сопряжённых корня:
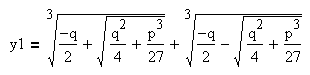
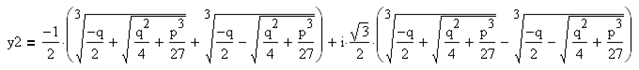
3. Дискриминант равен нулю. В этом случае уравнение имеет три действительных корня, и два корня из трёх обязательно совпадают друг с другом. Рассуждая точно так же, как в случае с положительным дискриминантом, учитывая равенство 
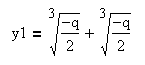
Итак, если дискриминант равен нулю, то уравнение имеет три действительных корня, и два корня из трёх обязательно совпадают друг с другом: 
Теперь получим решение исходного кубического уравнения 
В зависимости от знака дискриминанта S возможны три случая:
· Если 
· Если 
· Если 
При этом: 
Реализация алгоритма в объектно-ориентированной среде программирования Delphi
Авторами статьи была создана программа в среде Delphi для решения кубических уравнений с использованием формулы Кардано по разработанному алгоритму, описанному выше.
Рис. 1 . Интерфейс программы для решения кубических уравнений.
Для решения уравнения пользователю необходимо ввести коэффициенты уравнения. Результат работы программы – коэффициенты уравнения в канонической форме (p и q), дискриминант (Q) и корни уравнения. Для создания интерфейса использовались следующие компоненты среды Delphi [5]:
· Label – для информирования пользователя о назначении программы, обозначения предназначения полей ввода – вывода;
· Button – для реализации основных действий программы (решения уравнения, очистки полей ввода-вывода, закрытия программы);
· Edit – для организации ввода-вывода данных;
· Panel и GroupBox – для группировки элементов на форме программы.
Рассмотрим код основных процедур программы.
Для решения уравнения необходимо объявить следующие переменные:
· A,B,C,D – коэффициенты исходного уравнения;
· p,q – коэффициенты преобразованного уравнения;
· F – аргумент комплексного корня;
· Re, Im – действительная и мнимая части комплексного корня;
· x1,x2,x3,y1,y2 – корни уравнения.
В программе предусмотрен контроль корректности ввода данных:
if (edit1.Text=») or (edit2.Text=») or (edit3.Text=») or (edit4.Text=») then
Showmessage(‘Введите все коэффициенты уравнения’);
Процедуры Clear_Koeffs и Clear_Results осуществляют очистку полей ввода-вывода.
Процедура вычисления коэффициентов и дискриминанта преобразованного уравнения имеет следующий вид:
edit5.Text := FloatToStr(p); edit6.Text := FloatToStr(q);
Вычисление корней уравнения происходит в зависимости от знака дискриминанта:
· Если дискриминант меньше нуля:
if q>0 then F:=Arctan(-2*Sqrt(-QQ)/q)+Pi;
if q=0 then F:=Pi/2;
if q=0 then x3:=-B/A/3;
Edit8.Text := FloatToStr(x1); Edit9.Text := FloatToStr(x2);
· Если дискриминант больше нуля:
if QQ>0 then begin
if -q/2+Sqrt(QQ)>0 then y1:=exp(ln(abs(-q/2+Sqrt(QQ)))/3);
if -q/2+Sqrt(QQ)=0 then y1:=0;
if -q/2-Sqrt(QQ)>0 then y2:=exp(ln(abs(-q/2-Sqrt(QQ)))/3);
if -q/2-Sqrt(QQ)=0 then y2:=0;
x1:=y1+y2-B/A/3; Re:=-(y1+y2)/2-B/A/3; Im:=(y1-y2)*Sqrt(3)/2;
Edit9.Text := FloatToStr(Re)+’ + i * ‘+FloatToStr(Im);
Edit10.Text:= FloatToStr(Re)+’ — i * ‘+FloatToStr(Im);
· Если дискриминант равен нулю:
if QQ=0 then begin
if q>0 then y1:=-exp(ln(abs(-q/2))/3);
Edit8.Text := FloatToStr(x1); Edit9.Text := FloatToStr(x2);
В программе также организован программный контроль ввода коэффициентов. Для этого создан обработчик события KeyPress для соответствующих элементов типа Edit [6]:
if not (Key in [‘-‘, ‘1’..’9′, #8]) then Key := #0.
В рамках проведенного исследования было рассмотрено несколько способов решения кубических уравнений, в том числе, с использованием формулы Кардано. Были изучены различные нюансы применения этого метода, а также проведено исследование зависимости получаемых результатов от знака кубического дискриминанта. В статье также приведен подробный алгоритм, разработанный авторами статьи, на основе тригонометрической интерпретации формулы Кардано, а также рассмотрены основные процедуры созданного программного обеспечения в объектно-ориентированной среде Delphi.
Существует довольно много проблем в различных научных областях, решение которых сводится к изучению методов решения уравнений третьей и выше степеней. Таким образом, можно сделать вывод, что актуальность проведенного исследования заключается в практическом применении рассмотренных методов, а также созданного программного обеспечения как при изучении некоторых тем математики, физики в школе и ВУЗах, так и при решении прикладных задач из различных областей.
1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. – М.: Наука, 1986.
2. Омельченко В.П., Э.В.Курбатова. Математика: учебное пособие. – Ростов н/Д.: Феникс, 2005.
3. Пичурин Л.Ф. За страницами учебника алгебры. – М.: Просвещение, 1990.
4. Корн Г., Корн Т. Справочник по математики для научных работников и инженеров. – М.: Наука, 1973.
5. Фленов М.Е. Библия Delphi. – С-Пб: БХВ-Петербург, 2011.
6. Архангельский А.Я. Delphi 7. Справочное пособие. – М.: Бином, 2004.
Поступила в редакцию 07.04.2014 г.
Презентация по теме: «Решение уравнений третьей степени»
НОУ. Презентация выступления ученика 11 класса Корнева Алексея по теме: «Решение уравнений третьей степени». Включает разработанную учеником компьютерную программу, для решения указанных уравнений.
Скачать:
| Вложение | Размер |
|---|---|
| Презентация по алгебре 10-11 класс. Тема «Решение уравнений третьей степени» (различными способами). | 1.01 МБ |
Предварительный просмотр:
Подписи к слайдам:
Выполнил: ученик 11 «а» класса Корнев Алексей Владимирович научный руководитель: Пузанова Наталья Анатольевна, учитель математики «Решение уравнений третьей степени» МБОУ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №68 г. Нижний Новгород 2014 год
ЦелЬ работы: Освоить решение кубических уравнений различными способами задачи: найти исторические сведения об открытии формул для решения кубических уравнений узнать новые способы решения создать несклько компьютерных программ для решения данных уравнений
Исторические сведения Николо Тарталья (1499-1557) Джироламо Кардано (1501-1576)
Понятие кубического уравнения Кубическое уравнение — алгебраическое уравнение третьей степени, ax 3 + bx 2 +cx-d=0 где a , b,c , d — коэффициенты, а х — переменная. Число x , обращающее уравнение в тождество , называется корнем или решением уравнения График кубического уравнения Любое кубическое уравнение можно привести к более простому виду -каноническому : y 3 +py+q=0
Способы решения Кубических уравнений: с помощью вынесения общего множителя; с помощью деления на многочлен; с помощью формулы Кардано ; с помощью теоремы Виета; с помощью схемы Горнера; решение возвратных уравнений; г рафический способ. с помощью компьютерных программ
Алгоритм решения: 1. Перегруппировать члены данного уравнения 2. Вынести общий множитель за скобки 3. Получить произведение равное нулю 4. Решить полученные уравнения. Решение кубических уравнений с помощью вынесение общего множителя за скобки
Алгоритм решения: 1. Подобрать один корень из делителей свободного члена 2. Поделить многочлен на многочлен 3.Найти корни в получившемся квадратном уравнении Решение кубических уравнений с помощью д еления многочлен на многочлен
Алгоритм решения: 1. Свести уравнение к каноническому виду ( добавить кононич . вид ) 2. Расчет корней по специальной формуле (добавить формулу) Решение кубических уравнений с помощью формулы Кардано
Алгоритм решения: 1. Подобрать корни, удовлетворяющие системе a x 3 + b x 2 + c x + d = 0 x 1 +x 2 +x 3 =-b/a x 1 x 2 +x 2 x 3 +x 3 x 1 =c/a x 1 x 2 x 3 =-d/a Решение кубических уравнений с помощью теоремы Виета ,где x 1 , x 2 , x 3 – корни уравнения
Не очень хорошо стоят индексы 1,2,3
Алгоритм решения: 1. По схеме Горнера найти корень уравнения 2. Решить получившееся квадратное уравнение Решение кубических уравнений с помощью схемы Горнера
Алгоритм решения: 1. Корнем уравнения является x=-1 2. Поделить многочлен на многочлен 3. Найти корни в получившемся квадратном уравнении Решение возвратных кубических уравнений
Алгоритм решения: 1. Разбить кубическое уравнение на два уравнения 2. Построить графики функций стоящих в левой и правой частях уравнения 3. Абсциссы точек пересечения графиков – корни заданного уравнения Графический способоб решения кубических уравнений
Старинные задачи, связанные с кубическими уравнениями
Решение кубических уравнений С помощью компьютерной программы Ознакомившись с кубическими уравнениями, я написал ещё программу для быстрого их решения. Метод , который будет использоваться в программе — перебор. Программа находит целочисленные корни находящиеся в промежутки от -100 до 100. Язык программирования: Pascal .
Итог моих исследований Просмотрев множество способов решения кубических уравнений, я остался верен двум на мой взгляд самым надёжным и практичным способам — это теорема Виета и схема Горнера, они позволяют быть уверенным в своем ответе. Теперь, выбирая между ними, мне стоит лишь посмотреть на сложность коэффициента уравнения.
Изображение алгоритма в виде блок-схемы
Блок-схемой называется наглядное графическое изображение алгоритма.
В блок-схеме отдельные этапы алгоритма изображают при помощи различных геометрических фигур – блоков.
Последовательность выполнения этапов указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями.
Типичные действия алгоритма изображаются следующими геометрическими фигурами:
Блок начала (конца) алгоритма
Надпись: «начало» («конец»).
Блок ввода-вывода данных
Надпись: «ввод» («вывод»)
и список переменных вводимых (выводимых).
Блок решения (арифметический)
Надпись: операция или группа операций.
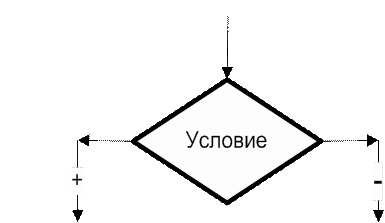
Надпись: логическое условие.
2.3. Составной оператор
Это группа операторов, отделенных друг от друга точкой с запятой, начинающихся с открывающей фигурной скобки < и заканчивающихся закрывающейся фигурной скобкой >.
Транслятор воспринимает составной оператор как один оператор.
2.4. Операторы ветвления
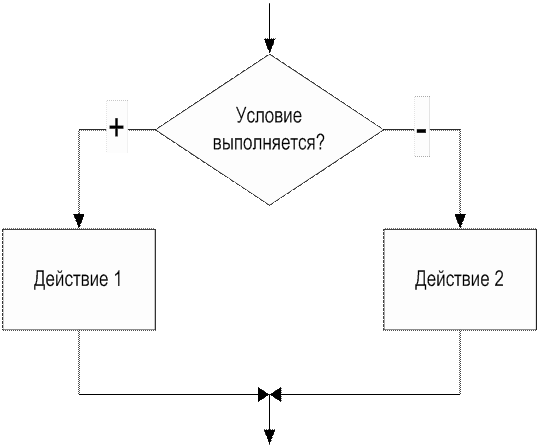
Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие.
Условный оператор, соответствующий приведенной блок-схеме, имеет вид:
if (выражение) оператор_1;
Вычисляется выражение. Если оно не равно нулю, т.е. имеет значение true, выполняется оператор_1, в противном случае (выражение равно нулю, т.е. false) – оператор_2.
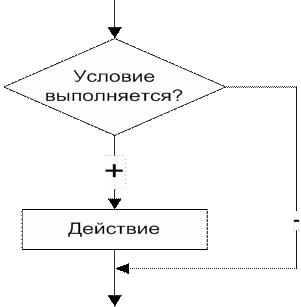
Если в зависимости от некоторого условия выполняется некоторое действие, а в противном случае ничего не происходит, то алгоритм имет вид:
Условный оператор в этом случаеимет конструкцию:
if (выражение) оператор;
Эту запись можно назвать «пропуск оператора else».
Здесь оператор либо выполняется, либо пропускается, в зависимости от значения выражения.
Если в какой-либо ветви условного процесса требуется выполнить несколько операторов, следует использовать составной оператор.
2.5. Примеры программ
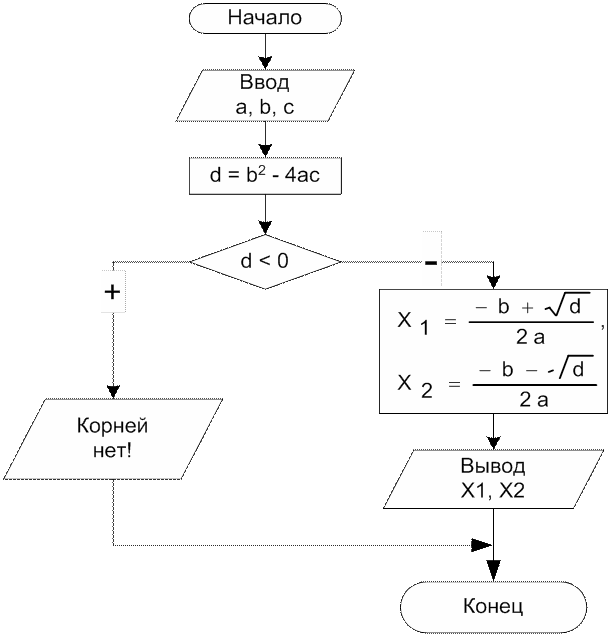
Задача 2. Известны коэффициенты а, b и с квадратного уравнения ax2+bx+c=0. Вычислить корни квадратного уравнения.
Входные данные: a, b, c.
Выходные данные: х1, х2.
printf(\n vvedite a \n);
printf(\n vvedite b \n);
printf(\n vvedite c \n);
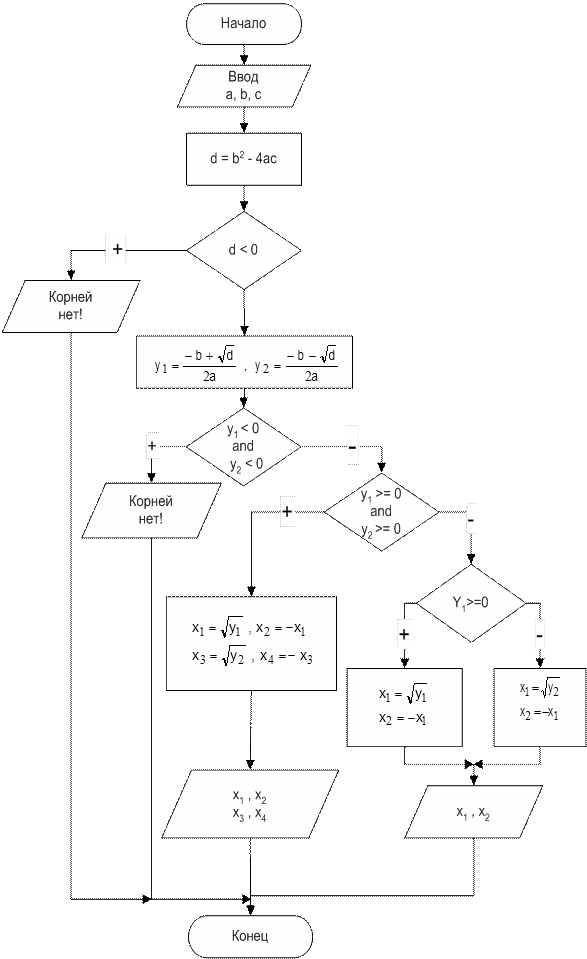
Задача 2. Решить ax4+bx2+c=0 биквадратное уравнение (y=x2).
Найти: х1, х2, х3, х4.
1. Вычисление дискриминанта уравнения d.
2. Если d ³ 0, определяются y1 и y2, а иначе корней нет.
3. Если y1, y20 , то корней нет.
4. Если y1, y2 ³0 , то вычисляются четыре корня по формулам 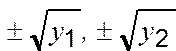
5. Если условия 3) и 4) не выполняются, то необходимо проверить знак 
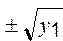
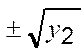
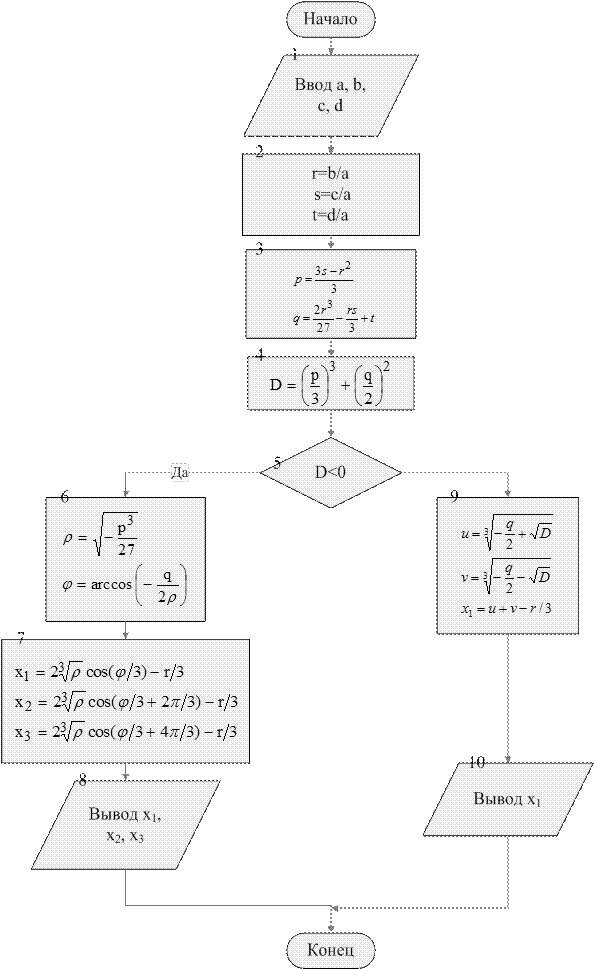
Задача 3.Решить кубическое уравнение:
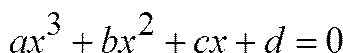
После деления на a уравнение (1) принимает канонический вид:
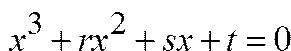
где 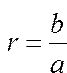
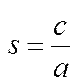
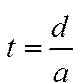
В уравнении (2) сделаем замену 
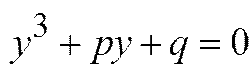
Где 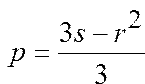
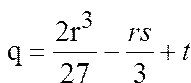
Число действительных корней приведенного уравнения (3) зависит от знака дискриминанта 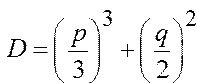
Количество корней кубического уравнения
| Дискриминант | Кол-во действительных корней |
| D?0 | |
| D |
При положительном дискриминанте кубического уравнения (3) действительный корень вычисляется по формулам:
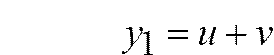
где 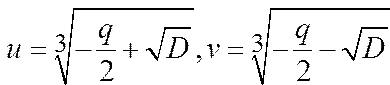
При отрицательном дискриминанте уравнение (3) имеет 3 действительных корня:
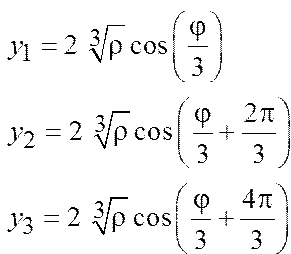
Где 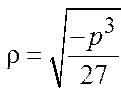
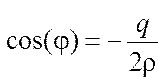
После расчета корней приведенного уравнения (3) по формулам (4) или (5) необходимо перейти к корням заданного кубического уравнения (1):
[1] Текстовые файлы, в которых содержится описание используемых в программе элементов.
[2] Служат для уточнения внутреннего представления и диапазона значений стандартных типов
[3] Поток – виртуальный канал связи, создаваемый в программе для передачи данных
Статьи к прочтению:
КИНОШНОЕ ИЗОБРАЖЕНИЕ — БЕЗ БЮДЖЕТА!
Похожие статьи:
Разработка алгоритмов для структурного программирования и их реализация ВВЕДЕНИЕ Современным пользователям и профессиональным программистам приходится…
Наименование Обозначение Функция Блок начало-конец(пуск-остановка) Элементотображает вход из внешней среды или выход из неё (наиболее частое применение?…
http://nsportal.ru/ap/library/drugoe/2014/11/29/prezentatsiya-po-teme-reshenie-uravneniy-tretey-stepeni
http://csaa.ru/izobrazhenie-algoritma-v-vide-blok-shemy/