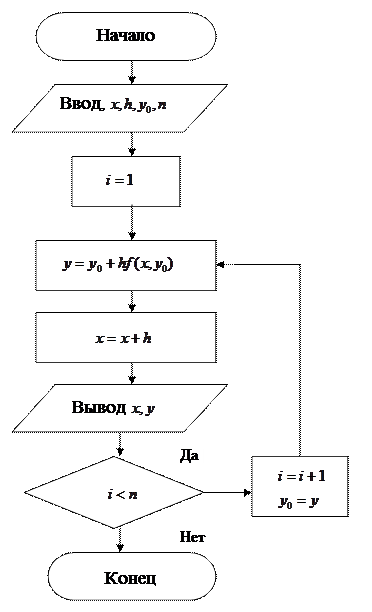
Блок схема решения дифференциальных уравнений

Блок-схема метода Эйлера.

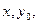
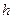
Задаются начальные значения величина шага и количество

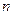
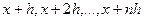
расчетных точек , как показано на рисунке 17.1. Решение получается в узлах . Вывод результатов предусмотрен на каждом шаге.

Рисунок 17.1 Блок-схема метода Эйлера.

Понятие решения краевой задачи.

Если при решении обыкновенных дифференциальных уравнений

задаются условия для двух значений независимой переменной (на концах рассматриваемого отрезка), то такие задачи называются краевыми.

Рассмотрим линейное дифференциальное уравнение второго порядка:

. (17.1)

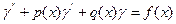
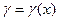
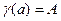
Краевая задача состоит в отыскании решения уравнения (17.1) на отрезке [а,b], удовлетворяющего на концах отрезка условиям

; . (17.2)

Граничные условия могут быть заданы не только в частном виде (17.2), но и в общем:

,

. (17.3)

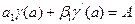
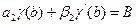
Методы решения краевых задач могут быть:

точные аналитические, приближенные и численные.

Решение дифференциального уравнения различными методами, доступными SIMULINK

Страницы работы

Содержание работы

Файл Модели\САМРаботы02\САМ06а.doc 5 стр. 200 Кбайт

1. Решение дифференциального уравнения различными методами, доступными SIMULINK.

Пусть, к примеру, требуется решить линейное дифференциальное уравнение второго порядка с правой частью

. (П7.01)

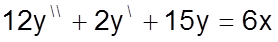
При использовании SIMULINK это уравнение можно решить несколькими способами.

Первый способ решения.

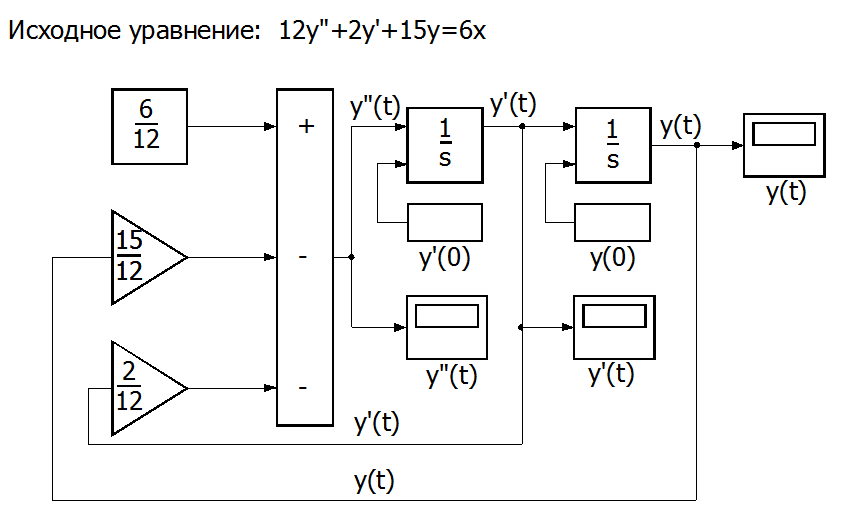
а) Разрабатывается блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain раздела Linear. Начнем с того, что разрешим его относительно второй производной

(П7.02)

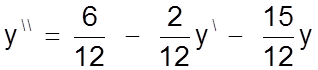
Полученное решение в модулях SIMULINK можно изобразить в виде

Рис. П7.1 Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain[1].

Для решения уравнения нами использованы 2 интегратора, 1 сумматор и 2 усилителя из раздела Linear библиотеки SIMULINK.

Вторая производная, согласно П7.02, должна получится путем вычитания из y₀ равного 6/12, производных, умноженных на соответствующие коэффициенты.

Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks — получатели] «y(t)».

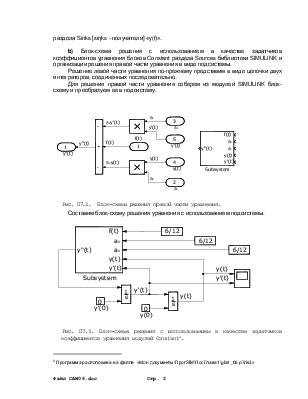
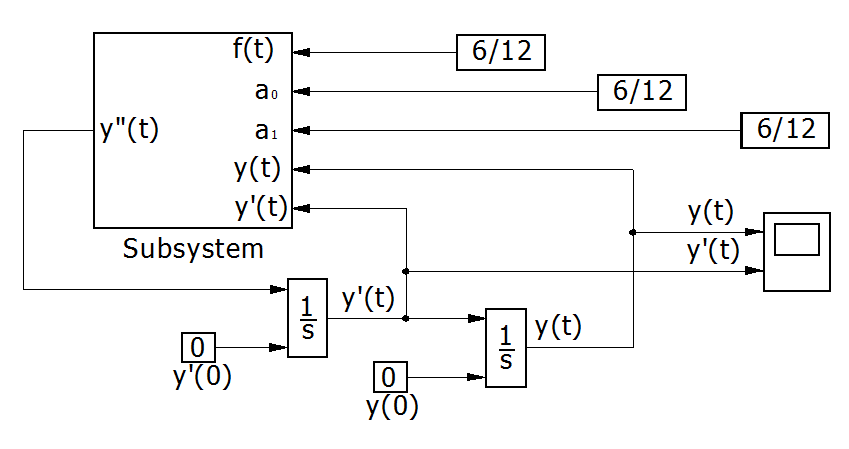
b) Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения блоков Constant раздела Sources библиотеки SIMULINK и организации решения правой части уравнения в виде подсистемы.

Решение левой части уравнения по-прежнему представим в виде цепочки двух интеграторов, соединенных последовательно.

Для решения правой части уравнения соберем из модулей SIMULINK блок-схему и преобразуем ее в подсистему.

Рис. П7.2. Блок-схема решения правой части уравнения.

Составим блок-схему решения уравнения с использованием подсистемы.

Рис. П7.3. Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Constant[2].

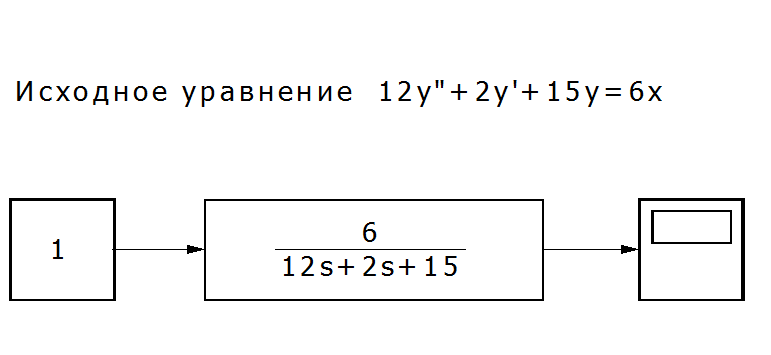
Второй способ решения.

Используя SIMULINK, можно представить другой способ решения этого уравнения. Решение можно получить, используя модуль Transfer Fcn [‘trænsfə: Fkn] (Передаточное звено). В качестве входного сигнала будем использовать блок Constant раздела Sources [so:s — источники]

Рис. П7.4. Решение уравнения с использованием типовых структурных схем[3].

Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks — получатели] «Интеграл».

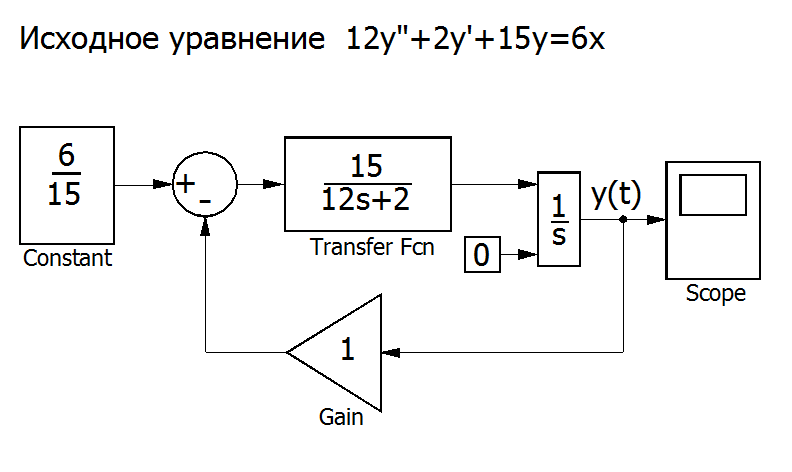
Третий способ решения.

SIMULINK может предложить еще один способ решения данного дифференциального уравнения. Воспользовавшись методами структурных преобразований, данное уравнение можно представить в виде структурной схемы, состоящей из типовых модулей.

Рис. П7.5. Решение уравнения с использованием структурных преобразований[4].

Проведем исследование дифференциального уравнения 2 порядка

(П8.01)

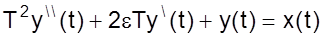
методами фазовой плоскости, используя возможности SIMULINK.

Начнем с того, что разрешим уравнение относительно старшей производной.

(П8.02)

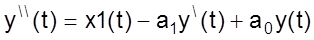
Решение левой части уравнения представим в виде цепочки из двух интеграторов соответственно настроенных.

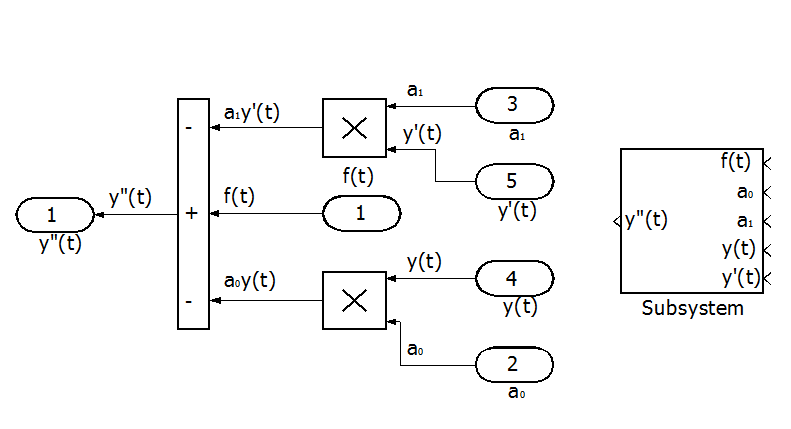
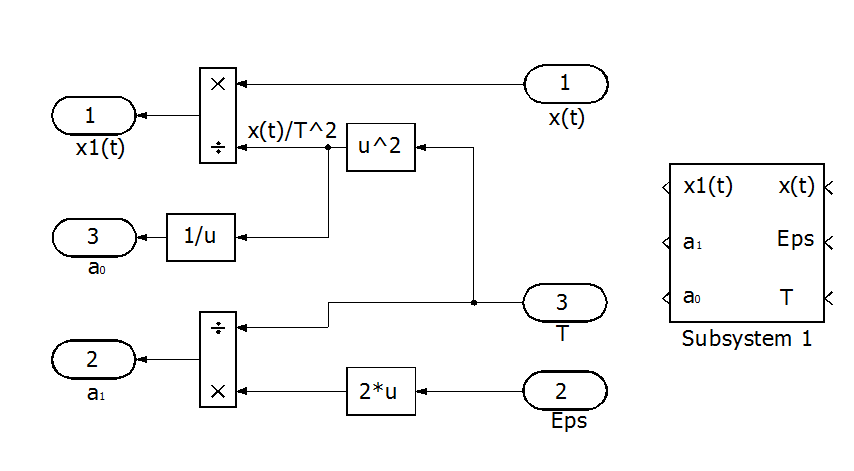
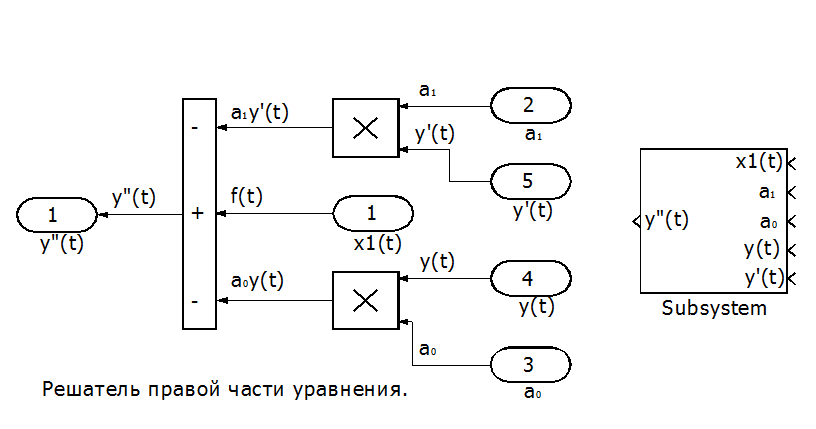
Для решения правой части уравнения создадим 2 подсистемы. Одну для формирования значений коэффициентов уравнения, разрешенного относительно старшей производной и вторую для решения собственно правой части уравнения.

Рис. П8.1 Блок-схема формирования коэффициентов уравнения.

Рис. П8.2. Решатель правой части уравнения.

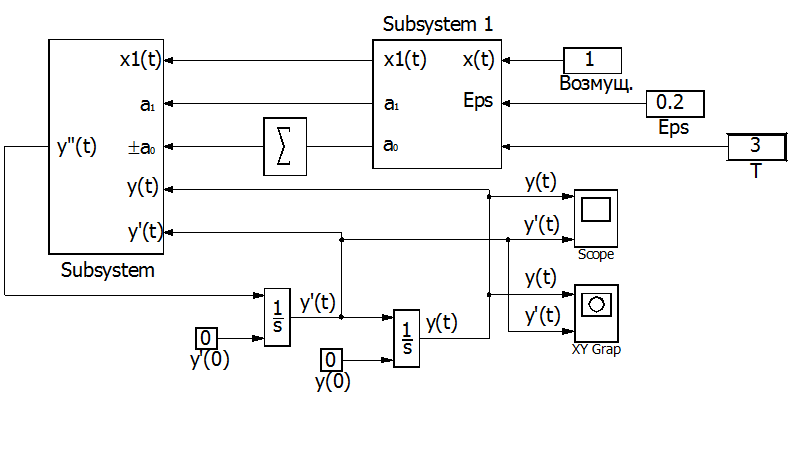
Решение дифференциального уравнения с учетом созданных подсистем будет иметь вид

Рис. П8.3. Блок-схема решения дифференциального уравнения[5].

Исследование фазового портрета.

Для наблюдения за фазовыми траекториями включим в качестве смотрового окна в блок-схему решения уравнения рис. П7.3 дополнительно модуль XY Graph из раздела Sinks библиотеки SIMULINK.

Сущность метода фазовой плоскости заключается в построении фазовых траекторий по дифференциальным уравнениям в системе координат: ось x — значение исследуемой величины u, ось y – скорость ее изменения du/dt. Процесс изменения траектории представляет собой движение изображающей точки на фазовой плоскости. Начальные условия определяют первоначальное положение изображающей точки на фазовой плоскости. Совокупность фазовых траекторий в плоскости (x, y) носит название фазовый портрет. Подробнее с методами фазовой плоскости можно ознакомиться по «Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. Учебник для вузов. Изд. 4-е, перераб. и доп. М., «Машиностроение», 1978. Стр. 485-495».

Задачей нашего исследования является построение некоторых наиболее характерных фазовых портретов.

Рассмотрим следующие случаи характерные для уравнения 2 порядка:

[1] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris1»

[2] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris3»

[3] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris4»

[4] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris5»

[5] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p8ris3»

Решение дифференциального уравнения 1-ой степени в Xcos

Визуальное моделирование динамических систем в Xcos

Перейдём, наконец к визуальному моделированию динамических систем в Xcos. Не секрет, что различные механические, физические, экономические и многие другие системы реальной жизни описываются в виде математических моделей на основе дифференциальных уравнений.

Рассмотрим порядок решения задачи Коши для дифференциального уравнения первого порядка с заданным начальным условием:

Аналитическое решения данного уравнения имеет вид:

Перейдём к построению блок-схемы в редакторе Xcos. Наша блок-схема будет состоять из двух частей: части, моделирующей найденное аналитическое решение задачи Коши (2) и части, отвечающей за численное интегрирование исходного дифференциального уравнения с заданными начальными условиями (1). Мы ни в коем случае не желаем запутать читателя или усложнить схему. Целью построения блок-схемы из двух является демонстрация идентичности решений – аналитического и численного.

Для моделирования блока аналитического решения нам понадобится единственный новый блок с палитры «Источники сигналов и воздействий» , необходимый непосредственно для генерации сигнала. Данный блок имеет только один регулярный выход и не имеет внутренних параметров; он необходим для подачи временных отсчетов, синхронизированных в соответствии с параметрами блоков CLOCK_c и END.

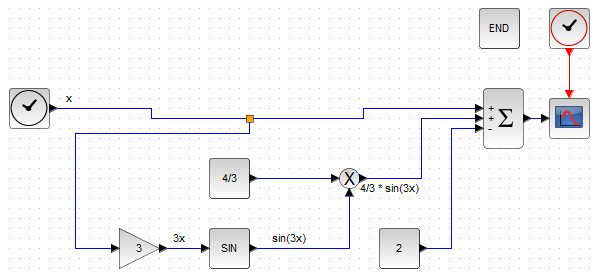
Итак, исходя из того, что моделируемое уравнение (2) имеем три слагаемых, нам понадобится блок BIGSOM_f, два входа которого будут положительными, а один, соответствующий константе «-2» — отрицательным. Сложносочинённым в моделируемом уравнении представляется второе слагаемое \( \frac<4><3>sin(3x) \), которое представляет из себя произведение константы \( \frac<4> <3>\) и синусоиды \( sin(\cdot) \), причём, аргумент синусоиды сам представляет собой увеличенный в три раза \( x \). Осуществлять вывод графиков моделируемых уравнений будет CMSCOPE. Блок-схема уравнения (2) представлена на рис. 30. Обратите внимание на использование блока GAINBLK_f, усиливающего исходный сигнал в три раза, а затем подающий его в функцию синуса.

Рисунок 30. Блок схема аналитического решения (2).

Теперь перейдём к реализации блок-схемы дифференциального уравнения первой степени в среде визуального моделирования Xcos.

Первое, что необходимо сделать – это привести дифференциальное уравнение к интегрируемому виду, где слева от знака «равно» стоит производная, а справа – остальные слагаемые. В рассматриваемом примере, уравнение (1) преобразуется к виду:

Далее, нам необходимо собрать из блоков Xcos правую часть уравнения (3), состоящую из двух слагаемых, а результат направить на блок интегрирования , который располагается на палитре «Системы с непрерывным временем». У блока INTEGRAL_f всего один внутренний параметр Initial state, в котором указывается значение в начальный момент времени. В нашем случае начальные условия заданы в (1) и имеют вид \( y(0)=-2 \), а значит, параметр Initial state блока INTEGRAL_f нужно установить равным -2. На выходе у блока-интегратора будет результат интегрирования правой части д.у. с н.у. (1), то есть численное решение исходной задачи Коши для дифференциального уравнения первой степени.

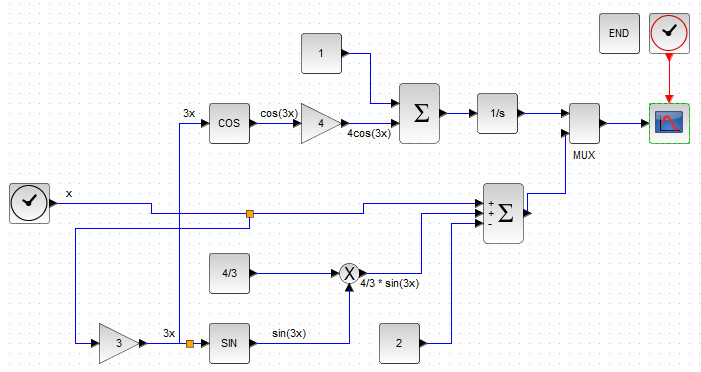
Итоговая блок-схема, выводящая аналитическое и численное решения на одну систему координат, представлена на рисунке 31.

Рисунок 31. Блок-схема вывода численного и аналитического решений з. Коши дифференциального уравнения

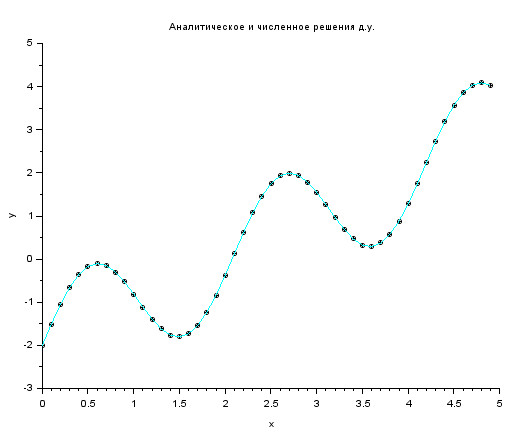
Моделирование проводилось на временном отрезке [0;5] с шагом дискретизации 0.1. Результат моделирования представлен на рис. 32.

Рисунок 32. Совпадающие численное (голубой график) и аналитическое (точечный график) решения.

Итак, нами рассмотрен подход к решению задачи Коши для ОДУ 1-ой степени.

Основные принципы данного подхода следующие:

Приведение дифференциального уравнения к виду, когда слева от знака «равно» находится только производная;

Использование блока TIME_f для подачи сигнала на вход функциональных блоков;

Использование блока INTEGRAL_f для поиска численного решения дифференциального уравнения;

Задание отрезка интегрирования во внутренних параметрах блока END, начальной точки и шага дискретизации в блоке CLOCK_c;

Возможность выбора численного метода поиска решения дифференциального уравнения в настройкам параметров интегрирования.