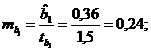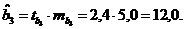Было оценено следующее уравнение регрессии

Оценка параметров уравнения регреcсии. Пример

Задание:
По группе предприятий, выпускающих один и тот же вид продукции, рассматриваются функции издержек:
y = α + βx;
y = α x β ;
y = α β x ;
y = α + β / x;
где y – затраты на производство, тыс. д. е.
x – выпуск продукции, тыс. ед.

Требуется:
1. Построить уравнения парной регрессии y от x :

• линейное;
• степенное;
• показательное;
• равносторонней гиперболы.

2. Рассчитать линейный коэффициент парной корреляции и коэффициент детерминации. Сделать выводы.
3. Оценить статистическую значимость уравнения регрессии в целом.
4. Оценить статистическую значимость параметров регрессии и корреляции.
5. Выполнить прогноз затрат на производство при прогнозном выпуске продукции, составляющем 195 % от среднего уровня.
6. Оценить точность прогноза, рассчитать ошибку прогноза и его доверительный интервал.
7. Оценить модель через среднюю ошибку аппроксимации.

1. Уравнение имеет вид y = α + βx
1. Параметры уравнения регрессии.
Средние значения

Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии

Коэффициент детерминации
R 2 =0.94 2 = 0.89, т.е. в 88.9774 % случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая

Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(1) = 4.01*1 + 99.18 = 103.19
y(2) = 4.01*2 + 99.18 = 107.2
. . .

2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;α/2) = (11;0.05/2) = 1.796
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.

Анализ точности определения оценок коэффициентов регрессии

S a = 0.1712
Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-20.41;56.24)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика

Статистическая значимость коэффициента регрессии a подтверждается

Статистическая значимость коэффициента регрессии b не подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (t_табл=1.796):
(a — t_табл·S_a; a + t_табл·S a)
(1.306;1.921)
(b — t_табл·S b; b + t_табл·S_b)
(-9.2733;41.876)
где t = 1.796
2) F-статистики

Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим

Примеры решения задач по множественной регрессии

Пример 1. Уравнение регрессии, построенное по 17 наблюдениям, имеет вид:

Расставить пропущенные значения, а также построить доверительный интервал для b₂ с вероятностью 0,99.

Решение. Пропущенные значения определяем с помощью формул:

Таким образом, уравнение регрессии со статистическими характеристиками выглядит так:

Доверительный интервал для b₂ строим по соответствующей формуле. Здесь уровень значимости равен 0,01, а число степеней свободы равно n – p – 1 = 17 – 3 – 1 = 13, где n = 17 – объём выборки, p = 3 – число факторов в уравнении регрессии. Отсюда

,

или . Этот доверительный интервал накрывает истинное значение параметра с вероятностью, равной 0,99.

Пример 2.Уравнение регрессии в стандартизованных переменных выглядит так:

.

При этом вариации всех переменных равны следующим величинам:

.

Сравнить факторы по степени влияния на результирующий признак и определить значения частных коэффициентов эластичности.

Решение.Стандартизованные уравнения регрессии позволяют сравнивать факторы по силе их влияния на результат. При этом, чем больше по абсолютной величине коэффициент при стандартизованной переменной, тем сильнее данный фактор влияет на результирующий признак. В рассматриваемом уравнении самое сильное воздействие на результат оказывает фактор х₁, имеющий коэффициент – 0,82, самое слабое – фактор х₃ с коэффициентом, равным – 0,43.

В линейной модели множественной регрессии обобщающий (средний) коэффициент частной эластичности определяется выражением, в которое входят средние значения переменных и коэффициент при соответствующем факторе уравнения регрессии натурального масштаба. В условиях задачи эти величины не заданы. Поэтому воспользуемся выражениями для вариации по переменным:

Коэффициенты b_j связаны со стандартизованными коэффициентами β_j соответствующим соотношением, которое подставим в формулу для среднего коэффициента эластичности:

.

При этом знак коэффициента эластичности будет совпадать со знаком β_j:

Пример 3. По 32 наблюдениям получены следующие данные:

Определить значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра а.

Решение. Значение скорректированного коэффициента детерминации определим по одному из формул для его вычисления:

Частные коэффициенты эластичности (средние по совокупности) вычисляем по соответствующим формулам:

Поскольку линейное уравнение множественной регрессии выполняется при подстановке в него средних значений всех переменных, определяем параметр а:

Пример 4. По некоторым переменным имеются следующие статистические данные:

Построить уравнение регрессии в стандартизованном и натуральном масштабах.

Решение.Поскольку изначально известны коэффициенты парной корреляции между переменными, начать следует с построения уравнения регрессии в стандартизованном масштабе. Для этого надо решить соответствующую систему нормальных уравнений, которая в случае двух факторов имеет вид:

или, после подстановки исходных данных:

Решаем эту систему любым способом, получаем: β₁ = 0,3076, β₂ = 0,62.

Запишем уравнение регрессии в стандартизованном масштабе:

Теперь перейдем к уравнению регрессии в натуральном масштабе, для чего используем формулы расчета коэффициентов регрессии через бета-коэффициенты и свойство справедливости уравнения регрессии для средних переменных:

Уравнение регрессии в натуральном масштабе имеет вид:

Пример 5.При построении линейной множественной регрессии по 48 измерениям коэффициент детерминации составил 0,578. После исключения факторов х₃, х₇ и х₈ коэффициент детерминации уменьшился до 0,495. Обоснованно ли было принятое решение об изменении состава влияющих переменных на уровнях значимости 0,1, 0,05 и 0,01?

Решение.Пусть — коэффициент детерминации уравнения регрессии при первоначальном наборе факторов, — коэффициент детерминации после исключения трех факторов. Выдвигаем гипотезы:

;

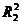
Основная гипотеза предполагает, что уменьшение величины было несущественным, и решение об исключении группы факторов было правильным. Альтернативная гипотеза говорит о правильности принятого решения об исключении.

Для проверки нуль – гипотезы используем следующую статистику:

,

где n = 48, p = 10 – первоначальное количество факторов, k = 3 – количество исключаемых факторов. Тогда

Сравним полученное значение с критическим F(α; 3; 39) на уровнях 0,1; 0,05 и 0,01:

На уровне α = 0,1 F_набл > F_кр, нуль – гипотеза отвергается, исключение данной группы факторов не оправдано, на уровнях 0,05 0,01 нуль – гипотеза не может быть отвергнута, и исключение факторов можно считать оправданным.

Пример 6. На основе квартальных данных с 2000 г. по 2004 г. получено уравнение . При этом ESS=110,3, RSS=21,4 (ESS – объясненная СКО, RSS – остаточная СКО). В уравнение были добавлены три фиктивные переменные, соответствующие трем первым кварталам года, и величина ESS увеличилась до 120,2. Присутствует ли сезонность в этом уравнении?

Решение. Это задача на проверку обоснованности включения группы факторов в уравнение множественной регрессии. В первоначальное уравнение с тремя факторами были добавлены три переменные, соответствующие первым трем кварталам года.

Определим коэффициенты детерминации уравнений. Общая СКО определяется как сумма факторной и остаточной СКО:

ТSS = ESS₁ + RSS₁ = 110,3 + 21,4 = 131,7

Проверяем гипотезы . Для проверки нуль – гипотезы используем статистику

Здесь n = 20 (20 кварталов за пять лет – с 2000 г. по 2004 г.), p = 6 (общее количество факторов в уравнении регрессии после включения новых факторов), k = 3 (количество включаемых факторов). Таким образом:

Определим критические значения статистики Фишера на различных уровнях значимости:

На уровнях значимости 0,1 и 0,05 F_набл> F_кр, нуль – гипотеза отвергается в пользу альтернативной, и учет сезонности в регрессии является обоснованным (добавление трех новых факторов оправдано), а на уровне 0,01 F_набл F_кр, и гетероскедастичность имеет место, а на уровне 0,01 F_набл

УМП+по+эконометрике. Учебнометодическое пособие по эконометрике с применением ms excel. Регрессионный анализ Пермь 2010 Содержание

Название	Учебнометодическое пособие по эконометрике с применением ms excel. Регрессионный анализ Пермь 2010 Содержание
Анкор	УМП+по+эконометрике.doc
Дата	19.09.2017
Размер	1.42 Mb.
Формат файла
Имя файла	УМП+по+эконометрике.doc
Тип	Учебно-методическое пособие #8713
страница	2 из 4

1. Построить линейное уравнение парной регрессии y по x .

2. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью F — критерия Фишера и t -критерия Стьюдента.

4. Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня.

5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

6. На одном графике отложить исходные данные и теоретическую прямую.
Решение

1. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 2.3.

Таблица 2.3

По формулам (2.5) находим параметры регрессии

Получено уравнение регрессии:

Параметр регрессии позволяет сделать вывод, что с увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб. (или 92 коп.).

После нахождения уравнения регрессии заполняем столбцы 7–10 таблицы 2.3.

1. Тесноту линейной связи оценит коэффициент корреляции (2.6):

Т.к. значение коэффициента корреляции больше 0,7, то это говорит о наличии весьма тесной линейной связи между признаками.

Это означает, что 52% вариации заработной платы ( y ) объясняется вариацией фактора x – среднедушевого прожиточного минимума.

Качество модели определяет средняя ошибка аппроксимации (2,7):

Качество построенной модели оценивается как хорошее, так как не превышает 10%.

1. Оценку статистической значимости уравнения регрессии в целом проведем с помощью F -критерия Фишера. Фактическое значение F — критерия по формуле (2.9) составит

Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы k₁=1 и k₂=12 — 2 =10 составляет F_табл= 4,96. Так как F_факт=10,41> F_табл= 4,96 , то уравнение регрессии признается статистически значимым.

Оценку статистической значимости параметров регрессии и корреляции проведем с помощью t -статистики Стьюдента и путем расчета доверительного интервала каждого из параметров.

Табличное значение t -критерия для числа степеней свободы и уровня значимости = 0,05 составит t_табл= 2,23.

Определим стандартные ошибки m_a, m_b, (остаточная дисперсия на одну степень свободы ):

Фактические значения t -статистики превосходят табличное значение:

поэтому параметры a , b и r_xyне случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительные интервалы для параметров регрессии a и b. Для этого определим предельную ошибку для каждого показателя:

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью p =1-α = 0,95 параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. являются статистически значимыми и существенно отличны от нуля.

4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: руб., тогда индивидуальное прогнозное значение заработной платы составит: руб.

5. Ошибка прогноза составит, согласно уравнения 2.13:

Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:

Доверительный интервал прогноза:

Выполненный прогноз среднемесячной заработной платы является надежным ( p =1-α =1- 0,05 = 0,95) и находится в пределах от 131,92 руб. до 190,66 руб.

6. В заключение решения задачи построим на одном графике исходные данные и теоретическую прямую (рис. 2.1):

2.3. Решение типовой задачи в MS Excel
C помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительных интервалов, остатки и графики подбора линии регрессии.

Если в меню сервис еще нет команды Анализ данных , то необходимо сделать следующее. В главном меню последовательно выбираем Сервис→Надстройки и устанавливаем «флажок» в строке Пакет анализа (рис. 2.2):

Далее следуем по следующему плану.

1. Если исходные данные уже внесены, то выбираем Сервис→Анализ данных→Регрессия.

2. Заполняем диалоговое окно ввода данных и параметров вывода (рис. 2.3):

Входной интервал Y – диапазон, содержащий данные результативного признака;

Входной интервал X – диапазон, содержащий данные признака-фактора;

Метки – «флажок», который указывает, содержи ли первая строка названия столбцов;

Константа – ноль – «флажок», указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист – можно указать произвольное имя нового листа (или не указывать, тогда результаты выводятся на вновь созданный лист).

Получаем следующие результаты для рассмотренного выше примера:

Откуда выписываем, округляя до 4 знаков после запятой и переходя

к нашим обозначениям:

Фактическое значение F -критерия Фишера:

Остаточная дисперсия на одну степень свободы:

Корень квадратный из остаточной дисперсии (стандартная ошибка):

Стандартные ошибки для параметров регрессии:

Фактические значения t -критерия Стьюдента:

Как видим, найдены все рассмотренные выше параметры и характеристики уравнения регрессии, за исключением средней ошибки аппроксимации (значение t -критерия Стьюдента для коэффициента корреляции совпадает с t_b). Результаты «ручного счета» от машинного отличаются незначительно (отличия связаны с ошибками округления).

3.Множественная регрессия и корреляция

Множественная регрессия – это уравнение связи с несколькими независимыми переменными:

где y – зависимая переменная (результативный признак); –независимые переменные (признаки-факторы).

Для построения уравнения множественной регрессии чаще используются следующие функции:

-линейная –

-степенная –

-экспонента –

-гипербола –

Можно использовать и другие функции, приводимые к линейному виду.

Для оценки параметров уравнения множественной регрессий применяют метод наименьших квадратов (МНК). Для линейных уравнений

(3.1)

строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:

(3.2)

Для двухфакторной модели данная система будет иметь вид:

(3.3)

Так же можно воспользоваться готовыми формулами, которые являются следствием из этой системы:

(3.4)

В линейной множественной регрессии параметры при x называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе:

(3.5)

где – стандартизированные переменные: для которых среднее значение равно нулю: , а среднее квадратическое отклонение равно единице: ;— стандартизированные коэффициенты регрессии.

В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии можно сравнивать между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.

Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений вида

(3.6)

где – коэффициенты парной и межфакторной корреляции.

Коэффициенты «чистой» регрессии b_iсвязаны со стандартизованными коэффициентами регрессии следующим образом:

(3.7)

Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (3.5) к уравнению регрессии в натуральном масштабе переменных (3.1), при этом параметр a определяется как

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением.

Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле

(3.8)

которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:

(3.9)

Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:

При линейной зависимости коэффициент множественной корреляции можно определить через матрицы парных коэффициентов корреляции:

– определитель матрицы парных коэффициентов корреляции;

– определитель матрицы межфакторной корреляции.

Так же при линейной зависимости признаков формула коэффициента множественной корреляции может быть также представлена следующим выражением:

(3.11)

где – стандартизованные коэффициенты регрессии; – парные коэффициенты корреляции результата с каждым фактором.

Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции

Для того чтобы не допустить преувеличения тесноты связи, применяется скорректированный индекс множественной детерминации, который содержит поправку на число степеней свободы и рассчитывается по формуле

(3.12)

где n – число наблюдений, m – число факторов. При небольшом числе наблюдений нескорректированная величина коэффициента множественной детерминации R 2 имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель.

Частные коэффициенты (или индексы) корреляции, измеряющие влияние на y фактора x_i , при элиминировании (исключении влияния) других факторов, можно определить по формуле

(3.13)

или по рекуррентной формуле:
(3.14)

Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от –1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты корреляции дают меру тесноты связи каждого фактора с результатом в чистом виде.

При двух факторах формулы (3.12) и (3.13) примут вид:

Значимость уравнения множественной регрессии в целом оценивается с помощью F -критерия Фишера:

(3.15)

Частный F -критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора x частный F -критерий определится как

(3.16)

Фактическое значение F -критерия Фишера сравнивается с табличным значением при уровне значимости и степенях свободы и . При этом, если фактическое значение — критерия больше табличного, то дополнительное включение фактора x_iв модель статистически оправданно и коэффициент чистой регрессии b_iпри факторе x_i статистически значим. Если же фактическое значение меньше табличного, то дополнительное включение в модель фактора x_i не увеличивает существенно долю объясненной вариации признака y , следовательно, нецелесообразно его

включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.

Оценка значимости коэффициентов чистой регрессии проводится по t -критерию Стьюдента. В этом случае, как и в парной регрессии, для каждого фактора используется формула

(3.17)

Для уравнения множественной регрессии (3.1) средняя квадратическая ошибка коэффициента регрессии может быть определена по формуле:

(3.18)

где – коэффициент детерминации для зависимости фактора x_iсо всеми другими факторами уравнения множественной регрессии. Для

двухфакторной модели (m = 2 ) имеем:

(3.19), (3.20)

Существует связь между t -критерием Стьюдента и частным F — критерием Фишера:

(3.21)

Уравнения множественной регрессии могут включать в качестве независимых переменных качественные признаки (например, профессия, пол, образование, климатические условия, отдельные регионы и т.д.). Чтобы ввести такие переменные в регрессионную модель, их необходимо упорядочить и присвоить им те или иные значения, т.е. качественные переменные преобразовать в количественные.

Такого вида сконструированные переменные принято в эконометрике называть фиктивными переменными. Например, включать в модель фактор «пол» в виде фиктивной переменной можно в следующем виде:

(3.22)

Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории (женский пол) к другой (мужской пол) при неизменных значениях остальных параметров.

3.2. Решение типовой задачи

По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%).