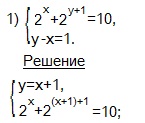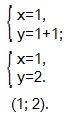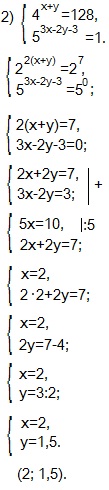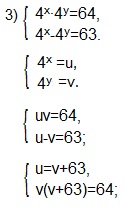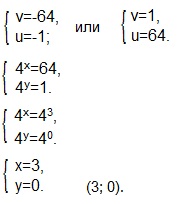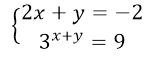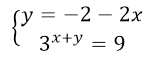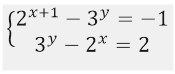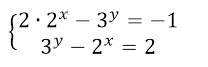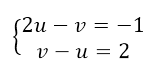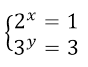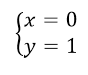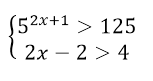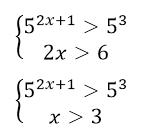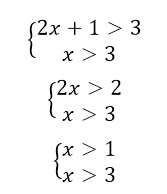11.3.6. Решение систем показательных уравнений
Что является обязательным при решении системы показательных уравнений? Конечно, преобразование данной системы в систему простейших уравнений.
Решить системы уравнений:
Выразим у через х из (2) -го уравнения системы и подставим это значение в (1) -ое уравнение системы.
Решаем (2) -ое уравнение полученной системы:
2 х +2 x +2 =10, применяем формулу: a x + y =a x ∙a y .
2 x +2 x ∙2 2 =10, вынесем общий множитель 2 х за скобки:
2 х (1+2 2 )=10 или 2 х ∙5=10, отсюда 2 х =2.
2 х =2 1 , отсюда х=1. Возвращаемся к системе уравнений.
Ответ: (1; 2).
Представляем левую и правую части (1) -го уравнения в виде степеней с основанием 2, а правую часть (2) -го уравнения как нулевую степень числа 5.
Если равны две степени с одинаковыми основаниями, то равны и показатели этих степеней — приравниваем показатели степеней с основаниями 2 и показатели степеней с основаниями 5.
Получившуюся систему линейных уравнений с двумя переменными решаем методом сложения.
Находим х=2 и это значение подставляем вместо х во второе уравнение системы.
Находим у.
Ответ: (2; 1,5).
Если в предыдущих двух примерах мы переходили к более простой системе приравнивая показатели двух степеней с одинаковыми основаниями, то в 3-ем примере эта операция невыполнима. Такие системы удобно решать вводом новых переменных. Мы введем переменные u и v, а затем выразим переменную u через v и получим уравнение относительно переменной v.
Решаем (2) -ое уравнение системы.
v 2 +63v-64=0. Подберем корни по теореме Виета, зная, что: v1+v2=-63; v1∙v2=-64.
Получаем: v1=-64, v2=1. Возвращаемся к системе, находим u.
Так как значения показательной функции всегда положительны, то уравнения 4 x = -1 и 4 y = -64 решений не имеют.
Представляем 64 и 1 в виде степеней с основанием 4.
Приравниваем показатели степеней и находим х и у.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение показательных уравнений.
Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение
Немного теории.
Показательная функция, её свойства и график
Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m
4) (ab) n = a n b n
7) a n > 1, если a > 1, n > 0
8) a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \( a \neq 1\)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.
3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.
Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2
Решить уравнение 3 х + 1 — 2 • 3 x — 2 = 25
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 (3 3 — 2) = 25, 3 х — 2 • 25 = 25,
откуда 3 х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2
Решить уравнение 3 х = 7 х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac<3^x> <7^x>= 1 \), откуда \( \left( \frac<3> <7>\right) ^x = 1 \), х = 0
Ответ х = 0
Решить уравнение 9 х — 4 • 3 х — 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 — 4t — 45 = 0. Решая это уравнение, находим его корни: t1 = 9, t2 = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2
Решить уравнение 3 • 2 х + 1 + 2 • 5 x — 2 = 5 х + 2 х — 2
Запишем уравнение в виде
3 • 2 х + 1 — 2 x — 2 = 5 х — 2 • 5 х — 2 , откуда
2 х — 2 (3 • 2 3 — 1) = 5 х — 2 ( 5 2 — 2 )
2 х — 2 • 23 = 5 х — 2 • 23
\( \left( \frac<2> <5>\right) ^
x — 2 = 0
Ответ х = 2
Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
Системы показательных уравнений и неравенств
Вы будете перенаправлены на Автор24
Способы решения систем уравнений
Для начала кратко вспомним, какие вообще существуют способы решения систем уравнений.
Существуют четыре основных способа решения систем уравнений:
Способ подстановки: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$
Способ сложения: в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении вместе обоих одна из переменных «исчезла».
Графический способ: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.
Способ введения новых переменных: в этом способе мы делаем замену каких-либо выражений для упрощения системы, а потом применяем один из выше указанных способов.
Системы показательных уравнений
Системы уравнений, состоящие из показательных уравнений, называются системой показательных уравнений.
Решение систем показательных уравнений будем рассматривать на примерах.
Решить систему уравнений
Решение.
Будем пользоваться первым способом для решения данной системы. Для начала выразим в первом уравнении $y$ через $x$.
Подставим $y$ во второе уравнение:
Ответ: $(-4,6)$.
Решить систему уравнений
Решение.
Данная система равносильна системе
Применим четвертый метод решения уравнений. Пусть $2^x=u\ (u >0)$, а $3^y=v\ (v >0)$, получим:
Решим полученную систему методом сложения. Сложим уравнения:
Тогда из второго уравнения, получим, что
Возвращаясь к замене, получил новую систему показательных уравнений:
Ответ: $(0,1)$.
Готовые работы на аналогичную тему
Системы показательных неравенств
Cистемы неравенств, состоящие из показательных уравнений, называются системой показательных неравенств.
Решение систем показательных неравенств будем рассматривать на примерах.
Решить систему неравенств
Решение:
Данная система неравенств равносильна системе
Для решения первого неравенства вспомним следующую теорему равносильности показательных неравенств:
Теорема 1. Неравенство $a^
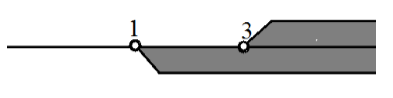
Изобразим оба решения на числовой прямой (рис. 11)
Рисунок 11. Решение примера 3 на числовой прямой
Ответ: $(3,+\infty )$
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 22 03 2021
http://www.math-solution.ru/math-task/exponential-equality
http://spravochnick.ru/matematika/pokazatelnaya_funkciya/sistemy_pokazatelnyh_uravneniy_i_neravenstv/