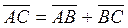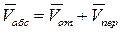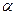Частные случаи движения точки
Частные случаи движения точки
Равномерное движение
Равномерным движением называется, как мы знаем, таксе движение, при котором точка за любые равные промежутки времени проходит равные расстояния.
Очевидно, что величина скорости в этом движении
Пусть в начальный момент 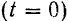
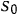
откуда расстояние точки от начала отсчета расстояний
Уравнение (71) определяет равномерное движение точки. Из формулы
где 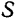
Скорость точки при равномерном движении (и только при этом движении) равна отношению пройденного пути ко времени. Так как модуль скорости точки остается постоянным при любом равномерном ее движении, то при этом всегда ее касательное ускорение
Отсюда следует, что касательное ускорение точки характеризует изменение ее скорости по величине.
При равномерном криволинейном движении точки ее скорость, оставаясь постоянной по модулю, изменяется только по направлению. Полное ускорение точки в этом случае равно нормальному ускорению, а
Отсюда следует, что нормальное ускорение точки характеризует изменение ее скорости по направлению.
Прямолинейное движение
При прямолинейном движении точки радиус кривизны ее траектории 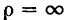
Следовательно, полное ускорение точки
При прямолинейном движении точка может иметь только одно касательное ускорение, и потому ее полное ускорение равно первой производной по времени от алгебраического значения скорости или второй производной по времени от пройденного ею пути.
Заметим, что так определяется ускорение точки только при прямолинейном ее движении.
В случае, если точка совершает прямолинейное и равномерное движение, то и нормальное
(следовательно, и полное) ускорения точки будут тождественно равны нулю. В этом движении точка не имеет никакого ускорения, так как ее скорость остается все время постоянной как по модулю, так и по направлению.
Равномерно переменное движение
Часто встречающимся на практике равномерно переменным (равномерно ускоренным или равномерно замедленным) движением точки называется такое ее движение, когда в равные, произвольно взятые промежутки времени алгебраическое значение скорости точки изменяется на одну и ту же величину.
Изменение алгебраического значения скорости точки характеризуется, как мы знаем, касательным ускорением. Отсюда следует, что при равномерно переменном движении точки алгебраическая величина ее касательного ускорения
Разделяя переменные и интегрируя уравнение в соответствующих пределах, будем иметь:
где 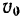
Для вывода уравнения движения точки воспользуемся зависимостью (67), из которой находим
и интегрируя это уравнение в соответствующих пределах, получаем:
Уравнение (74) представляет собой уравнение равномерно переменного движения точки. Из формулы
аналогичным образом находим
В этих формулах 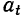
Формулы (73), (74) и (74а) одинаково справедливы как для прямолинейного, так и для криволинейного равномерно переменного движения точки. При прямолинейном движении точки радиус кривизны траектории 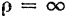
Следовательно, в этом случае ее полное ускорение 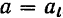
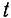
Гармоническое колебательное движение
Гармоническим колебанием точки называется такое ее движение, при котором расстояние s точки от начала отсчета изменяется по закону:
где 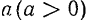
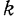
Так как значения 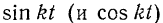
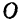
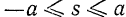
Наибольшее расстояние а, на которое точка удаляется от начала отсчета, называется амплитудой колебания.
Время 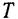
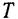
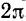
Отсюда находим, что период колебания точки
Постоянная 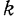
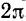
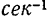
Пример задачи:
Поезд, двигаясь по закруглению пути равномерно ускоренно, приобретает через 3 мин после отхода от станции скорость
Определить ускорение поезда через 2 мин после отхода от станции, если радиус закругления пути
Решение:
из формулы (73) определяем касательное ускорение поезда:
Так как движение поезда — равномерно ускоренное, то его касательное ускорение постоянно.
Нормальное же ускорение поезда, определяемое формулой (69),
зависит от скорости движения и будет различным для разных моментов времени.
Определяем скорость поезда в конце второй минуты после отхода его от станции
Тогда нормальное ускорение поезда в этот момент будет равно
Ускорение (полное) поезда в конце второй минуты
Пример задачи:
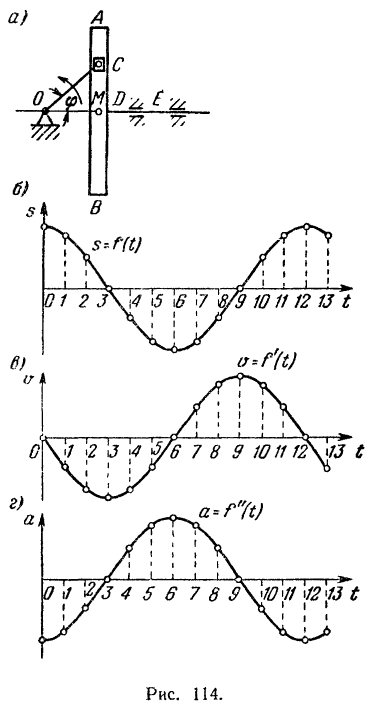
Жестко связанная с направляющей 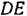
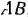
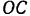

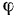
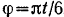
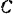
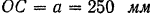
Решение:
При вращении кривошипа рама 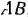

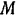

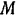

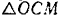
Обозначив расстояние 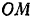
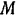

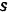
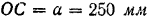
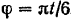
Полученное уравнение (I) аналогично уравнению (75).
Точка 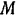
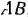

и период колебаний
За 12 секунд кривошип 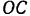
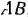
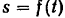
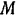
Дифференцируя по времени уравнение движения точки 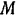
Графиком скорости 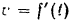
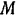
Так как точка 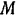
Графиком ускорения 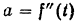
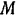
Из уравнения (1) движения точки 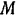
Следовательно, в этот момент точка 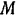
При дальнейшем движении точки 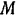

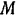
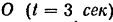
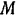

Таким образом, когда точка находится в центре 
В рассмотренном примере мы имели дело с прямолинейным движением точки, но гармонические колебания точка может совершать и по любой криволинейной траектории. Характер движения точки будет тот же, только при этом надо иметь в виду, что при криволинейном движении, кроме касательного ускорения, точка имеет еще и нормальное ускорение.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Частные случаи движения
а) Прямолинейное движение.
В этом случае траекторией движения точки является прямая линия, причем ее радиус кривизны равен бесконечности ( 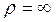
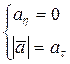
Векторы скорости и ускорения в этом случае располагаются на той же прямой, что и траектория, поэтому можно говорить, что они изменяются только численно, т. е. касательное ускорение характеризует изменение скорости по модулю.
б) Равномерное криволинейное движение.
Движение называется равномерным, если точка движется с постоянной по величине скоростью. Если скорость постоянная, то, следовательно, ее производная равна нулю, т. е.:

Так как в этом случае ускорение появляется только за счет изменения направления скорости, то нормальное ускорение характеризует изменение скорости по направлению.
В этом случае определим закон движения, проинтегрировав выражение (1.39)
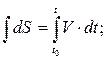
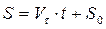
где S0 – координата начального положения материальной точки.
Движение без ускорения ( 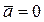
в) Равнопеременное криволинейное движение.
Движение называется равнопеременным, если оно происходит с постоянным касательным ускорением. Если ускорение положительно, такое движение называют равноускоренным, а если отрицательно – равнозамедленным.
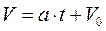
S= 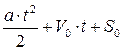
где V0 – скорость точки в начальный момент времени.
1.2.3. Движение материальных тел
В теоретической механике рассматриваются только абсолютно твердые тела. Движение всех материальных тел можно определенным образом классифицировать и рассматривать, как ведут себя характеристики движения применительно к каждому типу движения. Причем будем считать движение тела определенным, только в том случае, если нами определены характеристики движения всех материальных точек, составляющих рассматриваемое тело.
Поступательное движение — это такое движение, при котором любой выделенный в теле отрезок перемещается оставаясь параллельным самому себе.
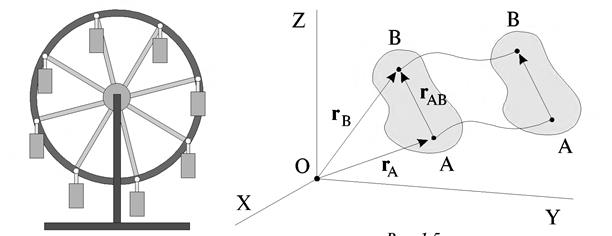
Классическим примером такого движения является движение кабинок колеса обозрения (рис. 1.32.а). Этот пример наглядно показывает, что поступательное движение — совсем не обязательно прямолинейное. Число степеней свободы тела в этом случае равно трем, так как достаточно описать движение какой-нибудь одной точки тела (например, точки А на рис. 1.32.б). Траектории всех остальных точек (например, точки В на рис. 1.32.б) могут быть получены путем «параллельного» переноса.
Рассмотрим некоторое тело, которое движется поступательно в выбранной системе координат (рис. 1.32.б). Выберем некоторый отрезок АВ внутри тела. Положение точек А и В определяют радиус – вектора 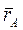
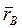
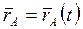
Тогда закон движения точки В будет иметь вид:

где rАВ — вектор, проведенный от точки А к точке В.
Скорость точки А:

Скорость точки В:
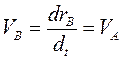
Так как rАВ — вектор, постоянный по величине (абсолютно твердое тело) и направлению (поступательное движение), ускорения точек А и В также равны между собой:

Таким образом, при поступательном движении тела законы движения всех его точек отличаются на постоянную величину, траектории при наложении совпадают, скорости всех точек равны между собой и ускорения также равны между собой.
Движение тела называют вращательным, если при его движении существуют, по крайней мере, две (а если тело плоское и движется в своей плоскости – то одна) точки тела, которые остаются неподвижными все время движения.
Линия, проходящая через эти две точки (если движение плоское, то перпендикулярно плоскости движения), называется осью вращения.
С таким движением мы сталкиваемся ежедневно, открывая и закрывая дверь в комнату. В этом случае тело обладает лишь одной степенью свободы, связанной с углом его поворота вокруг оси. При этом все точки тела движутся по окружностям, лежащим в плоскостях перпендикулярных оси вращения с центрами окружностей, лежащими на этой оси.
Существенно, что линейные скорости точек, находящихся на разном расстоянии от оси вращения, разные. В этом можно убедиться, касаясь стальной проволокой вращающегося диска точила (рис. 1.33), чем дальше от оси, тем длиннее сноп искр — тем больше скорость соответствующей точки диска.
При этом также видно, что искры летят по касательной к окружности, описываемой данной точкой диска. Ясно, что угловое перемещение всех точек твердого тела за одно и то же время будет одинаковым. Это обстоятельство позволяет ввести общую кинематическую характеристику — угловую скорость:
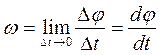
где 
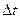
Зная 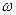
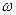

При этом величина скорости:

Очевидно, что точку О на оси вращения можно выбрать произвольно — значение r= rA sin α будет одним и тем же. Ускорение точки А:
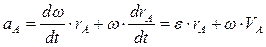
Здесь 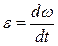
Таким образом, ускорение аА является суммой двух величин:
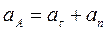
Причем все три вектора аА, аτ. и аn лежат в плоскости, перпендикулярной оси вращения (рис. 1.35).


Поскольку нормальное и касательное ускорения всегда перпендикулярны друг другу, то модуль полного ускорения:
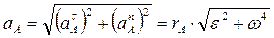
Таким образом, определены характеристики всех точек тела при его вращательном движении.
Движение тела называется плоскопараллельным, если траектория любой точки тела располагается в определенной плоскости все время движения и плоскости движения всех точек тела совпадают или параллельны между собой.
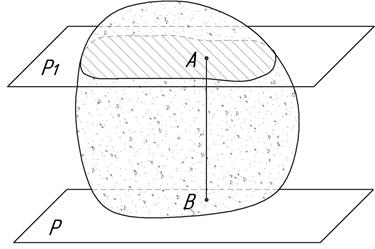
Рассмотрим тело, которое движется плоскопараллельно (рис. 1.36), т.е. заранее можно указать такую плоскость Р, что плоскости движения всех точек тела будут параллельны этой плоскости. Возьмем некоторую точку А тела и проведем ее плоскость движения Р1, а также перпендикуляр к этой плоскости АВ.
Все точки, которые лежат на АВ, должны иметь точно такие же характеристики движения, что и точка А. В противном случае расстояние между ними невозможно было бы сохранить, поскольку они двигаются в параллельных плоскостях, и была бы нарушена гипотеза абсолютно твердого тела.
Таким образом, задача сводится к рассмотрению движения плоского тела в своей плоскости (сечение тела плоскостью Р1 на рис. 1.36). Поэтому плоскопараллельное движение можно называть плоским.
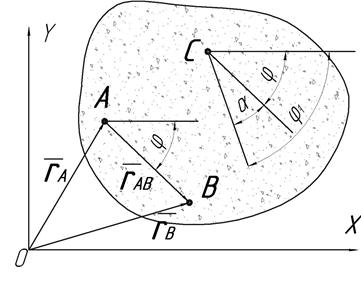
Рассматриваем плоскую задачу о движении тела (рис. 1.37). Выберем произвольную точку этого тела А (на практике следует выбирать такую точку, характеристики движения которой заранее известны). Эту точку назовем полюс и рассмотрим как выражаются характеристики движения других точек тела через характеристики движения полюса. Проведем радиус-векторы точек А и В – 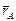
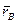
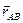
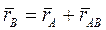
Продифференцировав равенство, получим:
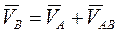
Поскольку вектор 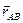
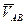

При этом законом плоскопараллельного движения тела следует считать две зависимости: 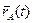
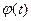
Теперь выберем в качестве полюса точку С (рис. 1.37), а угол поворота будем характеризовать некоторым углом 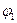
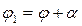
где 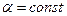
Дважды последовательно продифференцировав равенство, получим:
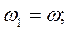
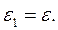
Следовательно, при плоскопараллельном движении поступательная часть движения зависит от выбора полюса ( 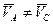
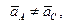
1.2.4. Теорема о проекциях скоростей двух точек тела
Теорема: проекции скоростей двух точек тела на линию, их соединяющую, равны.
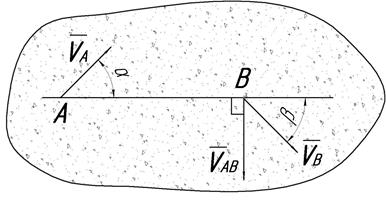
Доказательство: рассмотрим движущееся тело, у которого известны в некоторый момент времени скорости точек А и В соответственно 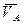
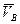
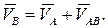
Поскольку 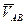
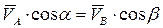
1.2.5. Мгновенный центр скоростей
Мгновенный центр скоростей – это такая точка сечения плоского тела (или жестко связанная с ним), скорость которой в данный момент времени равна нулю.
Теорема: при плоском непоступательном движении тела мгновенный центр скоростей всегда существует только один.
Доказательство: рассмотрим некоторое движущееся тело, имеющее в данный момент времени в точках А и В скорости 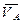
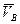
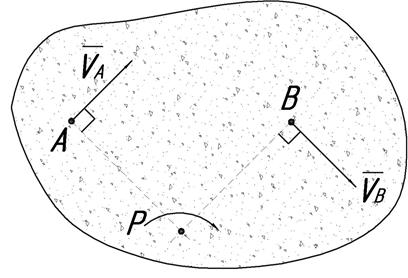
Из теоремы о проекциях скоростей двух точек тела следует, что проекции скоростей всех точек, лежащих на линии АР также должны быть равны нулю, т. е. скорости этих точек должны быть либо перпендикулярны линии АР, либо быть равными нулю. Но, то же самое можно сказать и про точки, лежащие на ВР – их скорости либо равны нулю, либо перпендикулярны ВР. Тогда про скорость точки Р можно сказать, что она равна нулю, поскольку быть одновременно перпендикулярной двум пересекающимся прямым она не может. Точка Р и есть мгновенный центр скоростей.
Единственность мгновенного центра также следует из приведенного доказательства, так как ни для какой другой точки проекции скоростей 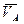
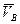
1. Для определения положения мгновенного центра скоростей необходимо знать направление скоростей двух точек тела. Мгновенный центр скоростей лежит на пересечении перпендикуляров к скоростям, проведенным из этих точек.
2. Чтобы определить угловую скорость вращения тела, необходимо знать положение мгновенного центра и величину скорости какой-либо точки тела. Угловая скорость равна отношению скорости любой точки тела к ее расстоянию до мгновенного центра скоростей. Если выбрать в качестве полюса мгновенный центр скоростей Р, то, поскольку его собственная скорость равна нулю, получим:
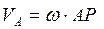
3. Чтобы определить скорость любой точки тела достаточно знать положение мгновенного центра скоростей и угловую скорость вращения тела. Скорость будет перпендикулярна линии, соединяющей рассматриваемую точку и мгновенный центр, а величина скорости равна произведению угловой скорости на расстояние от точки до мгновенного центра скоростей. Направление скорости следует выбирать в соответствии направлением вращения.
4. Отношение скорости любой точки тела к ее расстоянию до мгновенного центра скоростей есть величина постоянная для всех точек тела в данный момент времени. Поскольку угловая скорость не зависит от выбора полюса и одинакова для всех точек тела, то ее можно выразить через скорости различных точек:
|
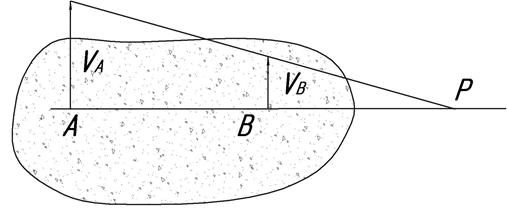
5. Чтобы определить положение мгновенного центра в случае, когда перпендикуляры к скоростям двух точек тела слились в одну линию, необходимо дополнительно провести линию через концы векторов скоростей. Ее пересечение с перпендикуляром к скоростям и будет мгновенным центром скоростей (рис. 1.40).
6. Если перпендикуляры к скоростям двух точек тела оказываются параллельными прямыми (не пересекаются), а также линия АВ не перпендикулярна к VА, то это значит, что тело движется поступательно или мгновенно поступательно и говорят, что мгновенный центр скоростей лежит в бесконечности.
1.2.6. Сложное движение точки.
Движение тела называется сложным, если оно регистрируется в подвижной системе координат. При этом движение тела относительно системы координат называется относительным, а движение самой системы координат – переносным.
Рассмотрим движение точки в подвижной системе координат (рис. 1.41). За малый промежуток времени 
Поскольку речь идет о малых перемещениях за малые промежутки времени, с незначительной погрешностью можно считать, что 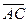
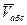
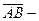
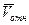
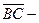
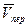
При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей (рис. 1.42).
|
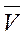
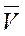
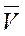
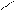

Сложение ускорений (теорема Кориолиса).
При сложном движении ускорение точки равно сумме трех ускорений:
относительного, переносного, кориолисова.
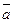
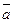
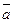
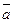
Относительное ускорение характеризует изменение относительной скорости только при относительном движении.
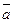
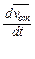
Переносное ускорение характеризует изменение переносной скорости только при переносном движении.
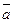
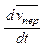
Кориолисово ускорение равно удвоенному произведению переносной угловой скорости на относительную скорость точки.
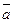
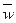
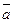
1.2.7. Пример расчета траектории движения точки.
По заданным уравнениям движения точки М установить вид ее траектории. Для момента времени t = t1, [c] определить: а) Положение точки на траектории; б) скорость точки; в) полное, касательное и нормальное ускорения; г) радиус кривизны траектории в соответствующей точке. Числовые данные варианта взять из приложения 5.
X = x (t) Y = y (t) t = 1 c.
Определим положение точки М на заданной траектории в момент времени t = 1 [c]. Подставим значение t в уравнения.
x = -4 ∙ 1 2 + 1 = -3, y = -3 ∙ 1 = -3; М (-3;-3)
Данные уравнения являются параметрическими, то есть зависят от параметра t и характеризуют траекторию движения точки М. Чтобы получить уравнение траектории в координатной форме необходимо исключить время t.
x = — 4t 2 + 1 y = — 3 t
4t 2 = 1 — x t 2 = (y / -3) 2
t 2 = (1 — x) / 4 t 2 = y 2 /9
Так как равны левые части уравнений, то приравняем правые части:
(1 — x) / 4 = y 2 /9; 1 – x = (4 ∙ y 2 )/9; x = — (4 ∙ y 2 )/9 + 1.
Полученное уравнение является уравнением траектории движения точки и уравнением параболы.
Для определения скорости точки М найдем проекции скорости точки на оси координат.
При t = 1 с проекции скорости на оси координат будут равны:
Модуль полной скорости определим по формуле:
v = 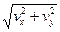
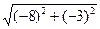
Для определения ускорения точки М найдем проекции ускорения точки на оси координат:
Модуль полного ускорения определим по формуле:
а = 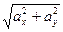

Определим нормальное и касательное ускорения.
Касательное ускорение определяется по формуле:
Знак + (at> 0) указывает на то, что движение точки М ускоренное.
Нормальное ускорение определяется по формуле:
an = 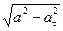
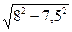
Определим радиус кривизны траектории движения точки М по формуле:
ρ = v 2 / an; ρ = 8,5 2 / 2,8 = 25,8 см.
По полученным результатам стром траекторию движения точки М (рис. 1.43). Отмечаем положение точки М на ней. Изображаем ее скорости и ускорения.
Сведем в таблицу полученные результаты:
| Координаты | Скорости; см/с. | Ускорения; см/с 2 . | Радиус кривизны; см | |||||||
| x | y | vx | vy | v | ax | ay | a | at | an | ρ |
| -3 | -3 | -8 | -3 | 8,5 | -8 | 7,5 | 2,7 | 25,8 |
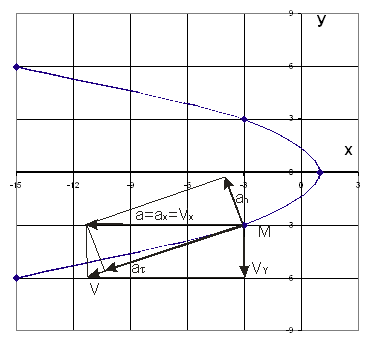
1.2.8. Пример расчета механизма на определение его скоростей и ускорений.
Механизм (рис. 1.44) состоит из ступенчатых колес 1, 2 и 3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны: r1= 2 см; r2 = 6 см; r3 =12 см; R1 =4с м; R2 = 8 см; R3 = 16 см. На ободьях колес расположены точки А, В и С. Числовые данные варианта взять из приложений 6 и 7. Схему варианта из приложения 8. Определить в момент времени t1 = 2с указанные в таблице скорости и ускорения соответствующих точек или тел.
Схема нагружения и исходные данные.
Составим расчетную схему:
Определим значение угловой скорости второго колеса, ω2: для этого определим закон изменения угловой скорости первого колеса:
Так как колесо 1 связано с колесом 3 ременной передачей, а ремень во всех точках имеет постоянную линейную скорость, то можно записать равенство:
Так как ремень соединяет колеса 1 и 3 по радиусам r1 и r2, то линейные скорости будут равны:
Так как равны левые части, то приравняем правые части равенств:
Второе и третье колеса связаны непосредственно по радиусам R2 и R3, аналогично определим закон изменения угловой скорости второго колеса:
При t = 2 с: ω 2 = 8 / 3 = 2,7; с -1 .
Определим линейную скорость рейки, v4:
Так как рейка 4 находится в зацеплении с первым колесом по радиусу R1, то в месте их зацепления линейные скорости колеса и рейки будет равны:
При t = 2 с: v4 = 16 ∙ 2 = 32; см/с.
Определим значение углового ускорения второго колеса, ε2:
Определим линейное ускорение заданной точки С, ас:
ас = 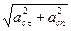
где a ct — линейное касательное ускорение точки С, см/с 2 ;
a cn — линейное нормальное ускорение точки С, см/с 2 ;
Так как точка С находится на втором колесе на радиусе R2, то:
При t = 2 с: acn = (4/3 ∙ 2) 2 ∙ 8 = 56,9 см/с 2 ,
ас = 
Определим линейное ускорение груза 5, а5:
Так как нить, удерживающая груз 5 намотана на второе колесо на радиусе r2, то в точке закрепления нити линейные скорости второго колеса и груза 5 равны:
Ответ: v4 = 32, см/с; ω 2 = 2,7, с -1 ; ε2 = 1,3, с -2 ; ас = 57,9, см/с 2 ; а5 = 8, см/с 2 .
Дата добавления: 2015-02-10 ; просмотров: 2925 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Частные случаи движения точки.
1. Равномерное движение – движение точки, при котором за равные промежутки времени она проходит одинаковые пути.
Таким образом, производная пути по времени будет постоянной величиной, а сам пройденный путь можно принять за дуговую координату. То есть, 
2. Равнопеременное движение – движение точки, при котором за равные промежутки времени ее скорость изменяется на одинаковые доли.
Таким образом, производная алгебраического значения скорости по времени будет постоянной величиной, т.е. будет постоянным тангенциальное (касательное) ускорение точки. То есть, 
3. Прямолинейное движение ‑ движение точки вдоль прямой. В этом случае 
Таким образом, полное ускорение точки равно нулю только при равномерном прямолинейном движении.
Тема 3: Кинематика твердого тела
Лекция 3. Теорема Грассгофа и виды движения твердого тела.
Определение абсолютно твердого тела, данное на первой лекции:
Абсолютно твердым телом называют такую совокупность
материальных точек, расстояния между которыми в процессе
движения остаются неизменными
является геометрическим. Наряду с этим утверждение, устанавливаемое следующей теоремой, лежит в основе кинематики твердого тела и считается, поэтому, кинематическим определением твердого тела.
Теорема Грассгофа
Проекции скоростей двух любых точек твердого тела на прямую, их соединяющую, одинаковы.
Действительно, пусть имеем две точки – А и В (рис. 3.1).
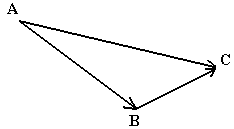
 Рисунок 3.1. К выводу теоремы Грассгофа Рисунок 3.1. К выводу теоремы Грассгофа | Соединим их вектором  . Тогда . Тогда  , следовательно, , следовательно,  и и  . Но . Но  , а , а  . Таким образом, . Таким образом,  . Окончательно, . Окончательно,  . . |
Очевидно, задачами кинематики твердого тела являются задание движения тела как целого и задание движения каждой его точки и определение по заданному закону движения тела его кинематических характеристик (угловой скорости и углового ускорения) и кинематических характеристик любой точки тела (траектории, скорости и ускорения). На первый взгляд, кажется, что задачи эти необъятные, однако это не так, о чем говорит следующее соображение.
Положение твердого тела вполне определяется треугольником, ему принадлежащим
Действительно, зная положение некоторого треугольника, принадлежащего телу, можно с ним связать систему декартовых координат, например, как показано на рис. 3.2. Такая система координат называется связанной. Тогда любая другая точка М тела будет иметь в этой системе координат постоянные абсциссу (xM), ординату (yM) и аппликату (zM). Таким образом, задать положение или движение твердого тела можно, задав положение треугольника в нем, или, что, то же самое, – положение связанной с ним системы координат относительно неподвижной системы отсчета. Таким образом, задача определения положения тела и его точек сводится к определению положения связанной системы координат относительно неподвижной.
Рисунок 3.2 ‑ К заданию движения твердого тела треугольником
Связанная система координат может двигаться относительно неподвижной 5-ю различными способами. В связи с этим различают 5 видов движения твердых тел.
1. Оси двух систем во все время движения параллельны друг другу. Это значит, любая прямая (ВC на рисунке 3.3), принадлежащая телу или жестко с ним связанная, останется параллельной своему первоначальному положению. То есть, в этом случае имеет место поступательное движение. Положение связанной системы координат будет определяться одной точкой – началом связанной системы координат. Обобщенными координатами, таким образом, в этом движении будут координаты этой точки – декартовые, естественные, цилиндрические, сферические и т.д.
Рисунок 3.3 ─ Поступательное движение
2. Системы координат имеют одну совпадающую ось. Она, как геометрическое место неподвижных точек, называется осью вращения, а движение тела будет вращательным. Так как прямая определяется двумя точками, то говорят, что вращательное движение твердого тела это движение тела с двумя неподвижными точками. В этом случае начала систем координат можно выбрать совпадающими, и одну из осей координат (например, Oz) расположить вдоль оси вращения. Положение связанной системы координат будет характеризоваться одним параметром – углом поворота вокруг общей оси (j на рисунке 3.4). Это и будет обобщенная координата при таком движении.
Рисунок 3.4 ─ Вращательное движение
3. Системы координат имеют одну общую плоскость. Свяжем с этой плоскостью одну из координатных плоскостей связанной системы (Oxy на рисунке 3.5). Движение связанной системы координат возможно только при скольжении одной плоскости по другой. Следовательно, при плоскопараллельном движении любая точка связанной системы координат будет находиться на неизменном расстоянии от этой плоскости (т. М и расстояние ММ1). Положение связанной СК определится обобщенными координатами – декартовыми координатами начала системы координат и углом поворота вокруг оси, перпендикулярной общей плоскости.
4. Системы координат имеют одну общую точку. Движение с одной неподвижной точкой называется сферическим. Это связано с тем, что, ввиду постоянства расстояний между точками твердого тела, всякая точка тела будет двигаться по сферической поверхности с центром в неподвижной точке тела. Положение связанной системы координат определится углами Эйлера (рисунок 3.6),Крылова и т.д., которые и будут обобщенными координатами при сферическом движении. Наряду с этим, в сферическом движении используют и системы избыточных обобщенных координат. Таковыми могут быть направляющие косинусы между осями систем координат (их 9, следовательно, избыточных – 6) или параметры Родрига-Гамильтона (компоненты кватернионов) – их 4, следовательно, избыточных – один. Для однозначности используют в этом случае дополнительные соотношения. Для косинусов – это 6 условий ортонормированности, для параметров Родрига-Гамильтона – условие нормировки.
 |  |
| Рисунок 3.5 ─ Плоскопараллельное движение тела | Рисунок 3.6 ─ Сферическое движение тела |
5. Наконец, связанная система координат не имеет ничего общего с неподвижной. Это свободное или пространственное движение. Обобщенными координатами в этом случае будут координаты начала связанной системы и углы Эйлера (рисунок 3.7),Крылова и т. д., направляющие косинусы, параметры Родрига-Гамильтона (как составляющие нормированного кватерниона, называемые в западной литературе параметрами Эйлера).
Рисунок 3.7 ─ Свободное пространственное движение твердого тела
Перейдем к рассмотрению этих видов движений твердого тела по отдельности.
http://helpiks.org/2-53922.html
http://lektsii.org/13-55482.html

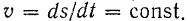
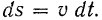
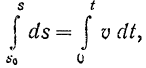
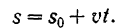
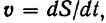
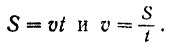
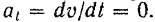
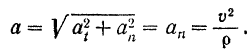
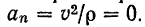
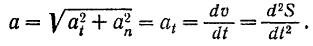
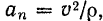
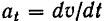
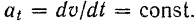
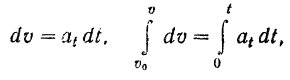
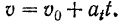
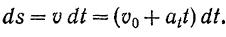
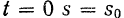
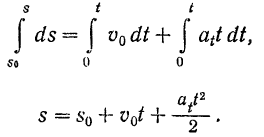
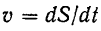
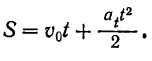
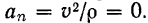
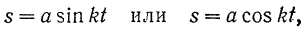
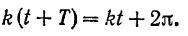
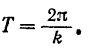
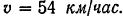
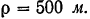
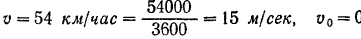
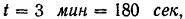
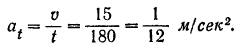
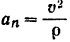
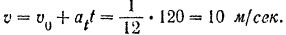
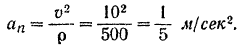
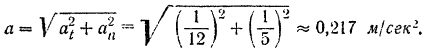
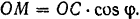
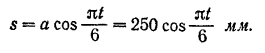
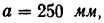
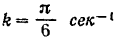
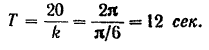
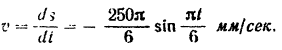
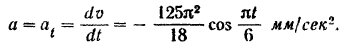
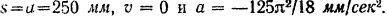




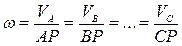 .
.