Частные случаи тригонометрических уравнений как запомнить

Статья «Легкие приемы запоминания не легкой тригонометрии»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Легкие приемы запоминания не легкой тригонометрии

(статья адресована обучающимся 9 – 11 классов и молодым учителям математики, преподающим в старших классах)

Математика – это один из самых сложных школьных предметов. Математика – наука абстрактная, именно поэтому многие учащиеся испытывают большие трудности при ее изучении.

Особенно тяжело приходится выпускникам 11-х классов, которые для сдачи экзамена по выбору взяли математику профильного уровня. Если при сдаче базового уровня математики разрешается использовать справочные материалы, то на экзамене по математике уровня профильного, выпускники остаются один на один со своей памятью. А она у всех разная, как, впрочем, и способности к математике.

Поэтому, задача учителя изыскать все способы, приемы запоминания формул учениками.

Остановимся на мнемонических правилах.

Мнемо́ника ( др.-греч. μνημονικόν — искусство запоминания ), мнемоте́хника — совокупность специальных приёмов и способов, облегчающих запоминание нужной информации и увеличивающих объём памяти путём образования ассоциаций (связей): замена абстрактных объектов и фактов на понятия и представления, имеющие визуальное , аудиальное или кинестетическое представление, связывание объектов с уже имеющейся информацией в памяти различных типов модификации для упрощения запоминания (Википедия).

Все мнемонические правила основаны на внесении ясности в, кажущийся бессмысленным, материал, т.е. хаос преобразуется в порядок посредством некоторой систематизации.

Вернемся к нашим старшеклассникам и поможем им легко запомнить некоторые тригонометрические формулы.

Значения синуса, косинуса, тангенса и котангенса основных углов.

Основное тригонометрическое тождество

sin 2 x + cos 2 x = 1, а также формулы

запоминаются учениками довольно легко.

Трудности начинаются, когда перед обучающимися ставится задача запомнить значения синуса, косинус, тангенса и котангенса основных углов:

Чтобы избавиться от этой проблемы можно (учитывая, что значения углов идут в порядке возрастания) записать цифры 1, 2, 3 сначала в прямом порядке, потом в обратном порядке в столбик:

разделить все записанные числа на 2:

и извлечь квадратный корень из числителей

Значения тангенса углов можно не запоминать, т.к. их вычисляем по известной формуле:

А значения котангенса записываются в обратном порядке.

Расположение углов на единичной окружности.

Расположение углов на единичной окружности запомнится легко, если записать их так:

Частные случаи простейших тригонометрических уравнений

Решение простейших тригонометрических уравнений вида: sin x = a , cos x = a, tg x = a , ctg x = a, где a – произвольное число.

Решите уравнение sin x = a, a ∈ [–1; 1].

Уравнение	Решение
sin x = -1
sin x = -√3/2
sin x = -1/2
sin x = 0
sin x = 1/2
sin x = √2/2
sin x = √3/2
sin x = 1

Решите уравнение cos x = a, a ∈ [–1; 1].

Уравнение	Решение
cos x = -1
cos x = -√3/2
cos x = -√2/2
cos x = -1/2
cos x = 0
cos x = 1/2
cos x = √2/2
cos x = √3/2
cos x = 1

Решите уравнение tg x = a

Уравнение	Решение
tg x = -√3
tg x = -1
tg x = -√3/3
tg x = 0
tg x = √3/3
tg x = 1
tg x = √3

Решите уравнение сtg x = a

Уравнение	Решение
сtg x = -√3
сtg x = -1
сtg x = -√3/3
сtg x = 0
сtg x = √3/3
сtg x = 1
сtg x = √3

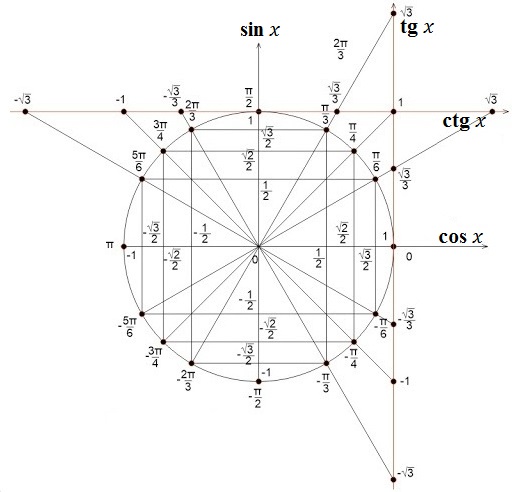
Все эти значения удобно находить по тригонометрическому кругу:

Ключевые слова: синус, косинус, тангенс, котангенс, tan, cot, от икс, чему равен, минус, корень из, пи, pi, π, делить на, равно.

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

1. Корни уравненияcosx=a.

При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a n arcsin a + 2πn, n ∈ Z (3)

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

1. Какие уравнения называют простейшими тригонометрическими?
2. Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
3. Выведите формулы решения простейших тригонометрических уравнений.
4. Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)