Частные способы решения квадратных уравнений

12 способов решения квадратных уравнений

В работе рассматриваются способы решения квадратных уравнений, которых нет в учебнике. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения кваратных уравнений при решении задач обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.

Просмотр содержимого документа
«12 способов решения квадратных уравнений »

1.Определение квадратного уравнения, его виды 4

2. Способы решения квадратных уравнений 4

2.1 Решение неполных квадратных уравнений. 4

2.2 Разложение левой части уравнения на множители. 1. СПОСОБ 5

2.3 Метод выделения полного квадрата. 2. СПОСОБ 5

2.4 Решение квадратных уравнений по формуле. 3. СПОСОБ 5

3.5 Решение уравнений с использованием теоремы Виета. 4. СПОСОБ 6

3.6 Решение уравнений с использованием теоремы Виета 5. СПОСОБ 6

3.7 Решение уравнений способом «переброски». 6. СПОСОБ 6

3.8 Свойства коэффициентов квадратного уравнения. 7. СПОСОБ 7

3.9 Графическое решение квадратного уравнения. 8. СПОСОБ 8

3.10 Решение квадратных уравнений с помощью

циркуля и линейки. 9. СПОСОБ 8

3.11 Решение квадратных уравнений с помощью номограммы. 10. СПОСОБ 9

3.12 Геометрический способ решения квадратных уравнений. 11. СПОСОБ 10

3.13 Способ решения квадратных уравнений по теореме Безу. 12. СПОСОБ 10

Список литературы 12

Приложение 2 ЗАДАЧИ

Приложение 3 Из истории квадратных уравнений

Уравнения второй степени умели решать еще в древнем Вавилоне. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид — при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактах.

Вывод формулы решения квадратного уравнения в общем, виде имеется у Виета. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Впервые квадратное уравнение сумели решить математики Древнего Египта.
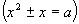
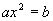
Неполные квадратные уравнения и частные виды полных квадратных уравнений умели решать вавилоняне (около 2 тыс. лет до н. э.). Об этом свидетельствует найденные клинописные тексты задач с решениями (в виде рецептов). Некоторые виды квадратных уравнений, сводя их решение к геометрическим построениям, могли решать древнегреческие математики. Приемы решения уравнений без обращения к геометрии дает Диофант Александрийский (III в.). В дошедших до нас шести из 13 книг «Арифметика» содержатся задачи с решениями, в которых Диофант объясняет, как надо выбрать неизвестное, чтобы получит решение уравнения вида . Способ решение полных квадратных уравнений Диофант изложил в книгах «Арифметика», которые не сохранились.

Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. итальянским математиком Леонардом Фибоначчи.

Общее правило решения квадратных уравнений, приведенных к виду 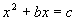, было сформулировано немецким математиком М. Штифелем (1487 — 1567). Выводом формулы решения квадратных уравнений общего вида занимался Виет. После трудов нидерландского математика А. Жирара (1595 — 1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.
Формулы, выражающие зависимость корней уравнения от его коэффициентов, были выделены Виетом в 1591 г.

И сейчас квадратные уравнения очень актуальны. Одна из основных тем ОГЭ – это квадратные уравнения.

Одной из основных тем, проверяемых на экзамене по математике, является тема «Квадратные уравнения». Данная тема изучается в 8 классе, а на повторение данной темы в 9 классе отводится один час. Я надеюсь , что эта работа поможет сдать экзамен по алгебре на более высокий бал.

Также квадратные уравнения используются в физике и в химии для решения задач в 10 и 11 класса, знание данной темы поможет при сдаче ЕГЭ по этим предметам.

Научиться решать квадратные уравнения различными способами.

Для достижения цели мы поставили перед собой следующие задачи

1.Изучить литературу по выбранной теме;

2.Изучить историю возникновения и решения квадратных уравнений;

3.Изучить способы решения квадратных уравнений разного вида;

4. Подобрать дидактический материал по теме работы

Объект исследования – квадратные уравнения.

При выполнении исследования применялись такие методы, как сравнительный анализ литературы, сбор и обработка фактов с помощью анализа, сравнения и аналогии.

1.Определение квадратного уравнения, его виды.

Определение: Квадратным уравнением называется уравнение вида

где х— переменная, а,b и с-некоторые числа, причем, а ≠ 0.

Коэффициенты а, b, с, различают по названиям: а – первый или старший коэффициент; b – второй или коэффициент при х; с – свободный член, свободен от переменной х.

Квадратное уравнение также называют уравнением второй степени, так как его левая часть есть многочлен второй степени

Квадратное уравнение называют приведенным, если старший коэффициент равен 1; квадратное уравнение называют неприведенным, если старший коэффициент отличен от 1.

х²+рх+q=0 – стандартный вид приведенного квадратного уравнения

кроме приведенных и неприведенных квадратных уравнений различают также полные и неполные уравнения.

Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля.

Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b и с равен нулю.

Обратите внимание: об ах² речи нет, этот член всегда присутствует в квадратном уравнении.

1) ах 2 + с = 0, где с ≠ 0;

2) ах 2 + bх = 0, где b ≠ 0;

Корнем квадратного уравнения ах²+вх+с=0 называют всякое значение переменной х, при котором квадратный трехчлен ах²+bх+с обращается в нуль; такое значение переменной х называют также корнем квадратного трехчлена.

Можно сказать и так: корень квадратного уравнения ах²+bх+с=0 – это такое значение х, подстановка которого в уравнение обращает уравнение в верное числовое равенство. 0=0.

Решить квадратное уравнение – это значит найти все его корни или установить, что их нет.

2.Способы решения квадратных уравнений

2.1 Решение неполных квадратных уравнений.

Сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать.

Теоретический материал по теме «10 способов решений квадратных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

10 способов решения квадратных уравнений

Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Многие практические задачи решаются с их помощью. Например, квадратное уравнение позволяет рассчитать тормозной путь автомобиля, мощность ракеты для вывода на орбиту космического корабля, траектории движения различных физических объектов – от элементарных частиц до звёзд.

В школе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения. Предлагаю 10.

Определение 1. Квадратным уравнением называют уравнение вида ах 2 + b х + с = 0, где коэффициенты а, в, с- действительные числа, а ≠ 0.

Определение 2 . Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых т.е. коэффициенты в и с отличны от нуля.

Неполное квадратное уравнение — это уравнение, в котором хотя бы один из коэффициентов в или, с равен нулю.

Определение 3. Корнем квадратного уравнения ах 2 + вх + с = 0 называют всякое значение переменной х, при котором квадратный трехчлен ах 2 + вх + с обращается в нуль.

Определение 4 . Решить квадратное уравнение — значит найти все его

корни или установить, что корней нет.

Разложение левой части уравнения на множители.

Решим уравнение х 2 + 10х — 24 = 0 .

Разложим левую часть на множители:

х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).

Следовательно, уравнение можно переписать так:

Произведение множителей равно нулю, если по крайней мере, один из его множителей равен нулю.

х + 12= 0 или х – 2=0

2. Метод выделения полного квадрата двучлена.

Решим уравнение х 2 + 6х — 7 = 0 .

Выделим в левой части полный квадрат:

тогда, данное уравнение можно записать так:

х + 3=4 или х + 3 = -4

3.Решение квадратных уравнений по формулам.

а) Решим уравнение:

б) Решим уравнение:

в) Решим уравнение: 2х 2 + 3х + 4 = 0,

Данное уравнение корней не имеет.

Ответ: корней нет.

4. Решение уравнений с использованием теоремы Виета.

Чтобы квадратное уравнение привести к приведенному виду, нужно все его члены разделить на a ,, тогда

сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

5. Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение

Умножая обе его части на а, получаем уравнение а 2 х 2 + а b х + ас = 0.

Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению у 2 + by + ас = 0,

Его корни у ₁ и у ₂ найдем с помощью теоремы Виета и окончательно:

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Решим уравнение 2х 2 – 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

Согласно теореме Виета

6. Свойства коэффициентов квадратного уравнения.

1. Пусть дано квадратное уравнение ах 2 + b х + с = 0, где а ≠ 0.

Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю),

А. Решим уравнение 345х 2 – 137х – 208 = 0.

Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то

Б. Решим уравнение 132х 2 – 247х + 115 = 0.

Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то

2) Решим уравнение 2х 2 + 3х +1= 0. Так как 2 — 3+1=0, значит х ₁ = — 1, х ₂ = -с/а= -1/2

Данный метод удобно применять к квадратным уравнениям с большими коэффициентами.

2. Если второй коэффициент уравнения b = 2 k – четное число, то формулу корней можно записать в виде

Решим уравнение 3х 2 — 14х + 16 = 0 .

Приведенное уравнение х 2 + рх + q = 0 совпадает с уравнением общего вида, в котором а = 1 , b = р и с = q . Поэтому для приведенного квадратного уравнения формула корней принимает вид

Формулу ( ) удобно использовать, когда р — четное число.

Пример. Решим уравнение х 2 – 14х – 15 = 0.

Решение. Имеем а=1, в =-14, (к=-7),с=-15.

7.Графическое решение квадратного уравнения.

И спользуя знания о квадратичной и линейной функциях и их графиках, можно решить квадратное уравнение так называемым функционально-графическим методом. Причем некоторые квадратные уравнения можно решить различными способами, рассмотрим эти способы на примере одного квадратного уравнения.

Пример. Решить уравнение =0

1способ . Построим график функции , воспользовавшись алгоритмом.

Значит, вершиной параболы служит точка (1;-4), а осью параболы – прямая x=1

2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки рис.2

х= -1 и х=3, тогда f (-1)= f (3)=0.

3) Через точки (-1;0) , (1;-4), (3;0) проводим параболу (рис 2).

Корнями уравнений являются абсциссы точек пересечения параболы с осью х; значит, корни уравнения

Преобразуем уравнение к виду .

Построим в одной системе координат графики функций и (рис 3 ).

Они пересекаются в двух точках A(-1;1) и B(3;9). Корнями уравнения служат абсциссы точек A и B , значит, .

3 способ

Преобразуем уравнения к виду.

Построим в одной системе координат графики функций и (рис.4) Они пересекаются в двух точках A(-1;-2) и В (3;6). Корнями уравнения являются абсциссы точек А и В, поэтому .

Преобразуем уравнение к виду , затем т.е.

Построим в одной системе координат параболу и прямую . Они пересекаются в точках А(-1;4) и В(3;4). Корнями уравнений служат абсциссы точек А и В, поэтому (рис.5) .

Рис.5

Разделим почленно обе части уравнения на x, получим:

Построим в одной системе координат гиперболу и прямую (рис.6). Они пересекаются в двух точках А(-1;-3) и В(3;1). Корнями уравнений являются абсциссы точек А и В, следовательно, .

Первые четыре способа применимы к любым уравнениям вида

ах 2 + b х + с = 0, а пятый- только к тем, у которых с не равно нулю.

Графические способы решения квадратных уравнений красивы, но не дают стопроцентной гарантии решения любого квадратного уравнения.

8. Решение квадратных уравнений с помощью циркуля и

Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + b х + с = 0 с помощью циркуля и линейки (рис.7 ).

Допустим, что искомая окружность пересекает ось

Центр окружности находится в точке пересечения перпендикуляров SF и SK , восстановленных в серединах хорд AC и BD , поэтому

Итак:

1) построим точки (центр окружности) и A (0; 1) ;

2) проведем окружность с радиусом SA ;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

2) Радиус окружности равен ординате центра ( AS = SB , или R = a + c /2 a ) , окружность касается оси Ох (рис.8б) в точке В(х ₁ ; 0) , где х ₁ — корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра

окружность не имеет общих точек с осью абсцисс (рис 8в), в этом случае уравнение не имеет решения.

Решим уравнение х 2 — 2х — 3 = 0 (рис.9).

Решение. Определим координаты точки центра окружности по формулам:

Проведем окружность радиуса SA , где А (0; 1).

9. Решение квадратных уравнений с помощью

Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.

Таблица XXII . Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен-

там определить корни уравнения.

Криволинейная шкала номограммы построена

по формулам (рис.10):

Полагая ОС = р, ED = q , ОЕ = а (все в см.), из

подобия треугольников САН и CDF получим

откуда после подстановок и упрощений вытекает уравнение

причем буква z означает метку любой точки криволинейной шкалы.

2) Решим с помощью номограммы уравнение

Разделим коэффициенты этого уравнения на 2,

3) Для уравнения z 2 — 25 z + 66 = 0 коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5 t , получим уравнение t 2 — 5 t + 2,64 = 0,

10. Геометрический способ решения квадратных уравнений.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.

1) Решим уравнение х 2 + 10х = 39.

В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.12).

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD , достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25) , т.е. S = х 2 + 10х + 25. Заменяя

х 2 + 10х числом 39 , получим, что S = 39 + 25 = 64 , откуда следует, что сторона квадрата ABCD , т.е. отрезок АВ = 8 . Для искомой стороны х первоначального квадрата получим

2) А вот, например, как древние греки решали уравнение у 2 + 6у — 16 = 0 .

Решение представлено на рис 13. где

Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой

один и тот же квадрат, а исходное уравнение у 2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у ₁ = 2, у ₂ = — 8 (рис. .

3) Решить геометрически уравнение у 2 — 6у — 16 = 0.

Преобразуя уравнение, получаем

На рис 14. находим «изображения» выражения у 2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3 . Значит, если к выражению у 2 — 6у прибавить 9 , то получим площадь квадрата со стороной у — 3 . Заменяя выражение у 2 — 6у равным ему числом 16,

получаем: (у — 3) 2 = 16 + 9, т.е. у — 3 = ± √25 , или у — 3 = ± 5, где у ₁ = 8 и у ₂ = — 2.