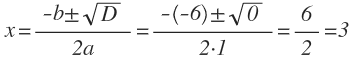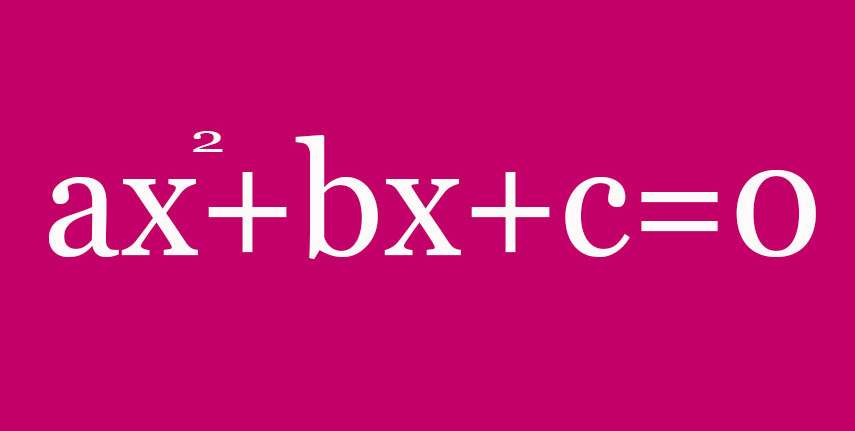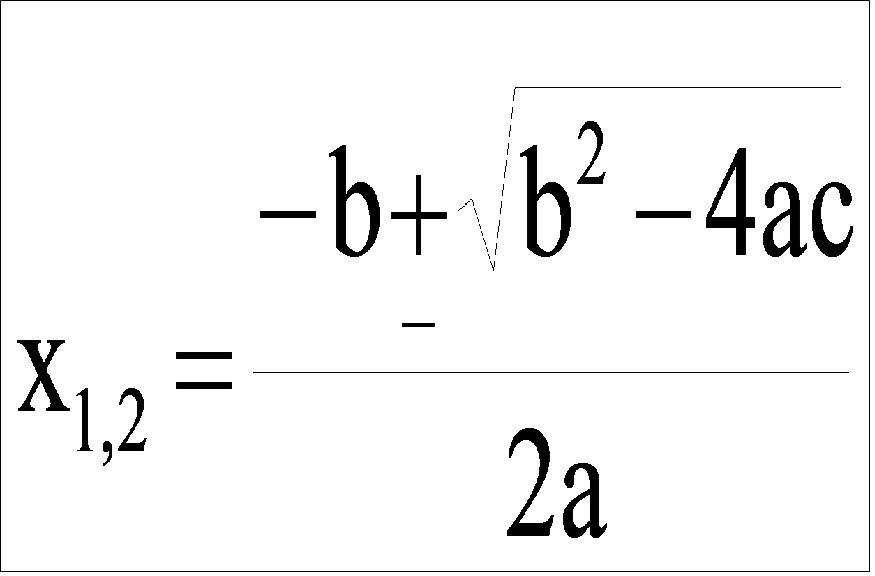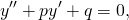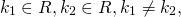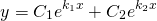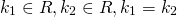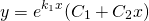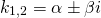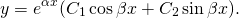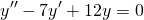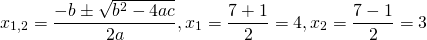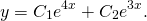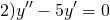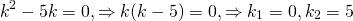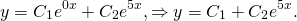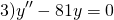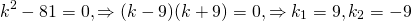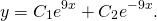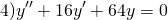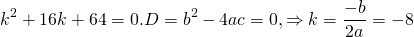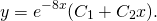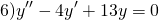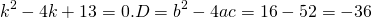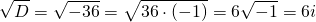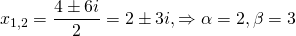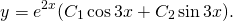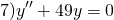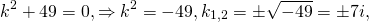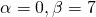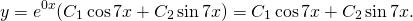Чему равен дискриминант уравнение второго порядка

Как найти дискриминант квадратного уравнения

О чем эта статья:

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

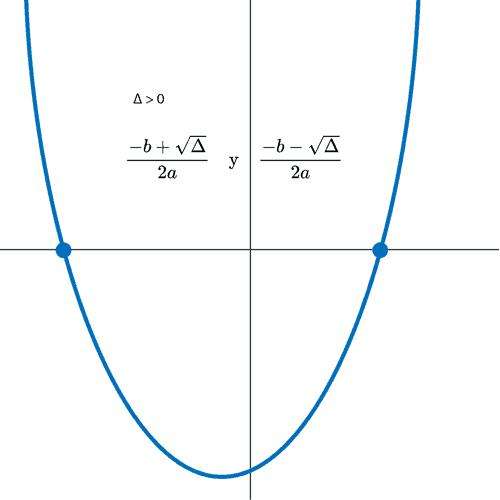
Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Формула решения квадратных уравнений и примеры ее использования

После изучения уравнений первого порядка в школах проходят тему квадратных равенств. Существует несколько методов их решения, однако применение формулы с дискриминантом является самым распространенным и универсальным. Рассмотрим в статье эту формулу решения уравнений квадратных.

Какие уравнения называются квадратными?

Ниже приведен рисунок, на котором изображено равенство, состоящее из трех слагаемых. Переменная x является неизвестной. Поскольку первый член содержит ее во второй степени, то данное выражение получило название квадратного. Латинскими буквами a, b и c в нем обозначены числовые коэффициенты.

Вам будет интересно: Какова площадь земного шара?

Это уравнение называют полным, поскольку в нем присутствуют все слагаемые, содержащие переменную во 2-й, 1-й и 0-й степенях (член c, называемый свободным, можно представить в виде c * x0).

Если один из коэффициентов b или c будет нулевым, тогда уравнение станет неполным. Заметим, что равенство нуля числа a автоматически преобразует рассматриваемое выражение в линейное уравнение.

Как для полных, так и для неполных равенств второго порядка можно использовать формулу решения уравнения квадратного через дискриминант.

Универсальная формула

Как было упомянуто выше, через дискриминант формула решения уравнения квадратного может использоваться для нахождения корней равенства второго порядка совершенно любого типа. Эта формула изображена на рисунке ниже.

Из нее видно, что уравнение максимум может иметь два решения (знак ±), однако если подкоренное выражение в знаменателе будет равно нулю, тогда неизвестный x, удовлетворяющий равенству, будет представлен единственным действительным числом. Формула решения уравнения квадратного демонстрирует также, что ее использование возможно в случае знания всех трех (или меньше для неполного уравнения) его коэффициентов.

Рассматриваемую формулу можно получить самостоятельно, для этого достаточно решить уравнение в общем виде с помощью метода дополнения до полного квадрата.

Отметим, что эту формулу для определения корней неполных уравнений нет необходимости использовать, поскольку существуют более простые методы решения (факторизация с помощью вынесения за скобки икса или простой перенос свободного члена в правую часть равенства и взятие корня из него).

Понятие дискриминанта и его значение

Если посмотреть еще раз на формулу решения уравнения квадратного через дискриминант, то последним будет называться разность, заключенная под знак корня в знаменателе, то есть b2 — 4 * a *c.

Какую роль он играет? Не зная об уравнении совершенно ничего, а имея только его дискриминант, можно с уверенностью сказать, сколько решений оно имеет, и какого они типа. Так, положительному значению дискриминанта соответствует 2 действительных решения, отрицательное его значение говорит также о 2-х решениях, но они уже будут комплексными числами. Наконец, если дискриминант равен нулю, что выполняется, когда b * b = 4 * a * c, то уравнение будет обладать лишь одним действительным корнем x.

Примеры решения равенств второго порядка

Используя формулу корней квадратного уравнения, решение уравнений квадратных приведем в задачах разного характера.

Задача № 1. Произведение некоторых 2-х чисел равно -84, а их сумма составляет 5. Нужно определить эти числа.

Составляем систему уравнений согласно заданному условию, получаем:

Выражаем из второго уравнения x1, подставляем его в первое:

(5 — x2) *x2 = -84 = -(x2)2 + 5 * x2

Теперь следует перенести члены с иксом и иксом в квадрате в левую часть и вычислить дискриминант:

(x2)2 — 5 * x2 — 84 = 0; D = 25 — 4 *1 * (-84) = 361

Воспользовавшись универсальной формулой, получаем значение корней уравнения:

x2 = (5 ± 19) / 2 = > x2 = (12; -7)

Чтобы получить x1, можно воспользоваться любым из уравнений системы. Подставляя известные значения x2, мы получим аналогичные числа для x1. Этот факт означает, что условию задачи удовлетворяет всего одна пара чисел, то есть -7 и 12.

Задача № 2. Теперь решим несколько необычную задачу. Ниже дано уравнение:

x2 − k * x + 36 = 0

Необходимо найти все значения k, которые приводили бы к единственному решению равенства.

Чтобы понять, как ответить на поставленный вопрос, следует вспомнить, что уравнения рассматриваемого типа имеет 1 корень только в том случае, если его дискриминант нулевой. То есть нам нужно найти этот дискриминант, откуда можно получить число k. Имеем:

D = k2 — 4 * 1 * 36 = 0

Полученное равенство называется чистым уравнением второго порядка (в нем нет коэффициента b). Решаем его:

Таким образом, если число k примет значение +12 или -12, то корень уравнения будет один.

Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид

где p и q — действительные числа. Рассмотрим на примерах, как решаются однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Решение линейного однородного однородного дифференциального уравнения второго порядка зависит от корней характеристического уравнения. Характеристическое уравнение — это уравнение k²+pk+q=0.

1) Если корни характеристического уравнения — различные действительные числа:

то общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

2) Если корни характеристического уравнения — равные действительные числа

(например, при дискриминанте, равном нулю), то общее решение однородного дифференциального уравнения второго порядка есть

3) Если корни характеристического уравнения — комплексные числа

(например, при дискриминанте, равном отрицательному числу), то общее решение однородного дифференциального уравнения второго порядка записывается в виде

Примеры решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

Найти общие решения однородных дифференциальных уравнений второго порядка:

Составляем характеристическое уравнение: k²-7k+12=0. Его дискриминант D=b²-4ac=1>0, поэтому корни — различные действительные числа.

Отсюда, общее решение этого однородного ДУ 2-го порядка есть

Составим и решим характеристическое уравнение:

Корни действительные и различные. Отсюда имеем общее решение данного однородного дифференциального уравнения:

В этом случае характеристическое уравнение

Корни различны и действительны. Поэтому общее решение однородного дифференциального уравнения 2-го порядка здесь

Поскольку корни действительны и равны, для этого дифференциального уравнения общее решение записываем как

Характеристическое уравнение здесь

Так как дискриминант — отрицательное число, корни характеристического уравнения — комплексные числа.

Общее решение этого однородного дифференциального уравнения второго порядка имеет вид

Отсюда находим общее решение данного диф. уравнения:

Примеры для самопроверки.

Найти общее решение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами: