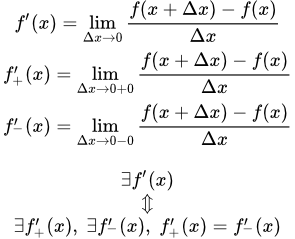Чему равна производная функции определяемой уравнением в точке

Определение производной функции в точке

Определение производной

В определении (1), приращение аргумента является одной переменной, хотя ее обозначение состоит из двух букв: и . Обычно переменную принято обозначать одной буквой или буквой с одним или несколькими индексами. Но приращение в математическом анализе настолько часто встречается, что его обозначают с небольшим нарушением правил. Приращение функции также является одной переменной.

В приведенном выше определении, является независимой переменной, а – зависимой. зависит от двух переменных. Если использовать выражение , то приращение функции зависит от переменных x и . Если использовать , то зависит от x и . Но когда мы вычисляем производную в заданной точке x , то считаем, что x является постоянной. Тогда является функцией, зависящей только от одной переменной . Таким образом задача о нахождении производной в точке x сводится к задаче о вычислении предела от функции , зависящей от одной переменной при , или от функции , зависящей от одной переменной при .

В правой части (1) мы сделали замену, и перешли от переменной к переменной . Тогда . При ,
.

После того, как мы нашли производную в заданной точке, то x уже можно считать не фиксированным числом, а переменной. То есть предел (1) можно рассматривать как функцию от x .

Еще раз подчеркнем, что выражение является функцией от двух переменных: x и . А выражение , полученное после вычисления предела, зависит только от одной переменной x .

Обозначение производной

Обозначение Лагранжа

Наиболее популярным является обозначение Лагранжа. Производную функции обозначают как и саму функцию, добавляя штрих после ее характеристики: . Если функция задана алгебраическим выражением, то это выражение заключают в скобки, и ставят знак штриха справа за закрывающей скобкой: . При этом производная также является функцией от той же переменной x , что и . Правда область определения производной может не совпадать с областью определения функции, а является ее подмножеством.

Напомним, что в обозначении функции фигурируют три символа: независимая переменная, характеристика функции и зависимая переменная (см. «Определение функции»). Так, в выражении
(2) ,
x является независимой переменной, или аргументом функции; f – характеристикой функции; y – зависимой переменной, или значением функции. Обозначение зависимой переменной может совпадать или не совпадать с обозначением характеристики. Производную функции (2) обозначают так:
.

Независимую переменную производной обозначают так же, как и независимую переменную функции. В нашем случае это x .

Характеристику производной обозначают тем же символом, что и характеристику функции, добавляя штрих справа: .

Зависимую переменную производной обозначают аналогично характеристике, добавляя штрих к обозначению зависимой переменной функции. Так, для примера (2), это будет : .

Если функция зависит от нескольких переменных, например
(3) ,
но все кроме одной считают постоянными, то к характеристике производной добавляют нижний индекс, обозначающий ту переменную, по которой вычисляют производную. При этом знак штриха может быть опущен. Например, следующие два обозначения эквивалентны: . Здесь подразумевается, что переменные и мы считаем постоянными. Тогда в данном контексте, является функцией от одной переменной . К зависимой переменной производной также добавляют нижний индекс переменной, по которой выполняется дифференцирование:
.
Подобные производные функций от нескольких переменных называются частными производными. Детально они будут рассмотрены позже.

Нижний индекс добавляют и при вычислениях, связанных со сложными функциями. Пусть, например, функцию можно представить как сложную: , составленную из двух функций: и . При этом множества значений функций и совпадают. Поэтому их удобно обозначить одной переменной y . Тогда производную от y , выраженную через переменную x , обозначают как :
.
А производную от y , выраженную через переменную , обозначают как :
.

Обозначение производной по времени в физике

В механике и физике, производную по времени обозначают не штрихом, а точкой над зависимой переменной. Обычно время обозначают буквой t . Тогда
.

Обозначение Лейбница

В способе Лейбница, зависимую переменную обозначают в форме отношения дифференциалов:
.
Этот способ удобен, поскольку указывает, по какой переменной ведется дифференцирование. Такой способ применяется только для функций от одной переменной. Для функций от многих переменных используют обозначение частной производной: .

Иногда в форме дифференциалов обозначают характеристику производной, добавляя справа аргумент:
.
Однако этот способ скорее неудачен, и может привести к путанице.

Обозначение Коши

Также, для обозначения производной, используют обозначение Коши:
.
Но мы не будем им пользоваться.

Существование производной

Рассмотрим вопрос о существовании предела, который используется при вычислении производной, при заданном значении x :
(4) .
Здесь могут возникнуть три случая:
1) в точке x существует конечный предел (4);
2) существует бесконечный предел или ;
3) предела (4) не существует.

1) Если существует конечный предел (4), то говорят, что функция имеет производную в точке x .

2) Если в некоторой точке x существует бесконечный предел (4), то говорят, что производной в этой точке не существует. Это согласуется с определением, ⇑ в котором указано, что производной называется конечный предел. Однако при этом говорят, что функция f имеет в точке x бесконечную производную, равную или . Здесь стоит обратить внимание на различие в определении предела и производной. Возможна ситуация, когда предел (4) существует (равный бесконечности), но при этом производная не существует (хотя существует ее значение, равное бесконечности).
См. пример ⇓.

3) Если предела (4) не существует, то функция не имеет производной в точке x .

Производные справа и слева

Определение

Лемма об односторонних производных

Функция имеет в точке x производную тогда и только тогда, когда она имеет в этой точке производные справа и слева, и они равны: . При этом
.

Пусть существует производная функции в точке x . Это означает, что она определена в некоторой окрестности точки x , и существует конечный предел функции при :
.
Но тогда существуют правая и левая окрестности точки x , на которых определена. По теореме об односторонних пределах, существуют равные правый и левый пределы:
.
Отсюда следует, что в точке x существуют односторонние производные
.

Пусть теперь, в точке x , существуют равные односторонние производные:
.
Это означает, что существуют правая и левая окрестности точки x , в которой определена . И существуют односторонние равные пределы:
.
Отсюда следует, что существует двусторонняя окрестность точки x , на которой определена . И по теореме об односторонних пределах, существует двусторонний предел:
.
Это означает, что в точке x существует производная
.

Следствие

Если функция имеет в точке x не равные односторонние производные, то она не имеет производной в этой точке.

Действительно, допустим противное. Пусть функция имеет в точке x не равные односторонние производные, но при этом имеет производную в этой точке. Тогда, согласно лемме об односторонних производных, она имеет в этой точке равные производные слева и справа, что противоречит предположению.

Примеры вычисления производной, используя определение

Все примеры Здесь и далее мы приводим подробные решения примеров, в которых нужно вычислить производную функции , используя определение производной ⇑.
решение ⇓ ; ⇓ ; ⇓ .

Пример

Все примеры ⇑ Найти производную функции , используя определение производной.

Функция определена для всех x . Поэтому она определена в любой окрестности любой точки x . Используем определение (1). Считаем, что x – фиксированное число, то есть что его значение задано. Найдем приращение функции в точке x :

.
Находим отношение приращения функции к приращению ее аргумента:
.
Находим предел функции , зависящей от переменной . При этом считаем, что x является фиксированным, заданным числом:
.

Итак, мы нашли производную:
.
Поскольку вычисленный нами предел существует, и является конечным числом для всех x , то функция имеет производную для всех значений аргумента x .

Пример бесконечной производной +∞

Все примеры ⇑ Найдем производную функции .

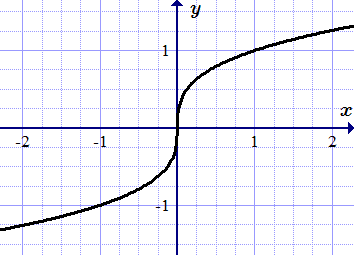
Производная функции в точке x = 0 равна плюс бесконечности.

Функция определена для всех x . Найдем отношение приращения функции к приращению ее аргумента в точке x :
.
Применим формулу . Тогда
;
(5) .
Считаем, что x является фиксированным числом. Тогда отношение является функцией от одной переменной : . При она определена для всех . При она определена для всех .

Пусть . Тогда:
.
Пусть . Подставим в (5) :
.
Поскольку , то
.

Таким образом мы нашли, что функция имеет производную для всех . При функция не имеет производной, она равна .

Пример

Все примеры ⇑ Найдем производную функции . Покажем, что несмотря на то, что функция определена для всех x , ее производная в точке не существует.

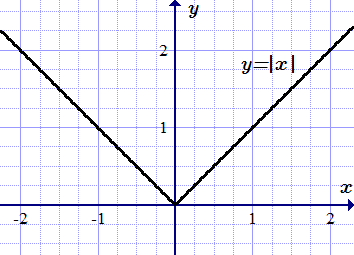
Функция y = |x| не имеет производной в точке x = 0 .

Функция определена для всех значений аргумента x . Поэтому она определена в любой окрестности произвольной точки x .

3. Рассмотрим точку . В ней
.
Найдем производную справа в точке . При этом ,
.
Теперь найдем производную слева в точке . В этом случае ,
.

Итак, мы нашли, что односторонние производные в точке существуют, но они не равны друг другу:
.
Согласно следствию леммы об односторонних производных, производной функции в точке не существует.

;
;
.
В точке производная не существует.

Использованная литература:
Г.Е. Иванов. Лекции по математическому анализу. Часть 1. Москва, МФТИ, 2018.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов . Опубликовано: 05-12-2020 Изменено: 08-11-2021

Производная, основные определения и понятия

Данная статья рассматривает основные понятия, для решения задач с производными с одной переменной.

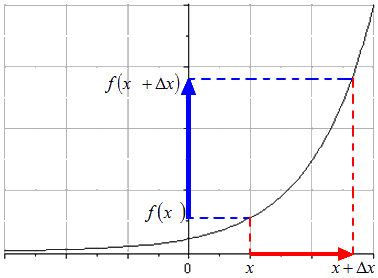
Пусть х – это аргумент функции f ( x ) и ∆ x возьмем малое число, не равное 0 . Значение ∆ x называют приращением аргумента функции и читают как «дельта икс». На рисунке видно, что красная линия относится для изменений аргумента от значения х до x + ∆ x .

Когда значение аргумента x 0 переходит к x 0 + ∆ x , тогда и значение функции меняется от f ( x 0 ) до f ( x 0 + ∆ x ) , если имеется условие монотонности функции из отрезка [ x 0 ; x 0 + ∆ x ] . Приращение функции f ( x ) – это разность f ( x 0 + ∆ x ) — f ( x 0 ) = ∆ f ( x ) приращения аргумента. Это приведено на рисунке, расположенном ниже.

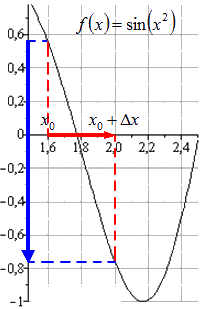
Для полного уяснения рассмотрим на конкретном примере. Если взять функцию f ( x ) = sin ( x 2 ) , тогда следует зафиксировать точку x 0 = 1 . 6 и приращение аргумента вида ∆ x = 0 . 4 . Тогда получим, что приращение функции при переходе от x 0 = 1 . 6 к x 0 + ∆ x = 1 . 6 + 0 . 4 = 2 будет равно:

∆ f ( x ) = ∆ sin ( x 2 ) = sin ( ( x 0 + ∆ x ) 2 ) — sin ( x 0 2 ) = = sin 2 2 — sin 1 . 6 2 = sin 4 — sin 2 . 56 ≈ — 1 . 306

Так как приращение ∆ f ( x ) отрицательное из отрезка [ 1 . 6 ; 2 ] , то это указывает на убывание функции. Обозначим это графически.

Определение производной функции в точке

Когда функция вида f ( x ) определена из промежутка ( a ; b ) , тогда x 0 и x 0 + ∆ x считаются точками данного промежутка. Производная функции f ( x ) в точке x 0 — это предел отношений приращения функции к приращению аргумента, когда ∆ x → 0 . Данное определение записывается как f ‘ ( x 0 ) = lim ∆ x → 0 ∆ f ( x ) ∆ x .

Если последний предел принимает конкретное значение, тогда существует конечная производная в точке. Когда предел бесконечен, то и сама производная бесконечна в этой точке. Когда предел не существует, то и производной в заданной точке не существует.

Функция f ( x ) дифференцируема в точке x 0 , если конечная производная в ней существует.

Когда функция вида f ( x ) дифференцируема в каждой точке из промежутка ( a ; b ) , тогда функцию называют дифференцируемой на заданном промежутке. Отсюда получаем, что любая точка х из промежутка ( a ; b ) может принимать значения функции f ‘ ( x ) , иначе говоря, имеет место определение новой функции вида f ‘ ( x ) , которая называется производной функции f ( x ) из интервала ( a ; b ) .

Нахождение производной иначе называют дифференцированием

Из выше указанного получаем, что производная в точке является числом, а производная функции на промежутке является функцией. Когда необходимо вычислять производную, обязательно обращаемся к нахождению переделов.

Найти производную функции sin ( 2 x ) в точке x 0 = π 6 .

Для нахождения производной в точке необходимо начать с написания предела отношения приращения функции к приращению аргумента, применив тригонометрические формулы. Получаем, что

( sin ( 2 x 0 ) ) ‘ = lim ∆ x → 0 ∆ sin ( 2 x 0 ) ∆ x = lim ∆ x → 0 sin ( 2 ( x 0 + ∆ x ) ) — sin ( 2 x 0 ) ∆ x = = lim ∆ x → 0 2 · sin 2 ( x 0 + ∆ x ) — 2 x 0 3 · cos 2 ( x 0 + ∆ x ) + 2 x 0 2 ∆ x = = 2 · lim ∆ x → 0 sin ( ∆ x ) · cos ( 2 x 0 + ∆ x ) ∆ x

Для упрощения используем первый замечательный предел и в результате получаем, что

( sin ( 2 x 0 ) ) ‘ = 2 · lim ∆ x → 0 sin ( ∆ x ) · cos ( 2 x 0 + ∆ x ) ∆ x = = 2 · lim ∆ x → 0 sin ( ∆ x ) ∆ x · lim ∆ x → 0 cos ( 2 x 0 + ∆ x ) = = 2 · 1 · cos ( 2 x 0 + 0 ) = 2 cos ( 2 x 0 ) = 2 cos 2 · π 6 = = 2 cos π 3 = 2 · 1 2 = 1

Ответ: ( sin ( 2 x 0 ) ) ‘ = 1 .

Найти производную функции f ( x ) = 3 x 3 — 1 из промежутка x ∈ 1 3 3 ; + ∞

Для поиска производной из интервала понимаем, что результат должен быть функцией. Тогда x 0 = x , где значение х возьмем любое число из заданного промежутка x ∈ 1 3 3 ; + ∞ . Из определения видно, что производной считают отношение приращения функции на приращение аргумента, который стремится к нулю. Запишем

f ‘ ( x ) = 3 x 3 — 1 ‘ = lim ∆ x → 0 f ( x + ∆ x ) — f ( x ) ∆ x = = lim ∆ x → 0 3 ( 3 + ∆ x ) 3 — 1 — 3 x 3 — 1 ∆ x = » open=» 0 0

Получаем неопределенность в результате. Поэтому следует произвести домножение на сопряженное выражение для применения формул сокращенного умножения, приведения подобных слагаемых и последующим сокращением выражения. Тогда получим, что

f ‘ ( x ) = lim ∆ x → 0 3 ( x + ∆ x ) 3 — 1 — 3 x 3 — 1 ∆ x = = lim ∆ x → 0 ( 3 ( x + ∆ x ) 3 — 1 — 3 x 3 — 1 ) ( 3 ( x + ∆ x ) 3 — 1 + 3 x 3 — 1 ) ∆ x · ( 3 ( x + ∆ x ) 3 — 1 + 3 x 3 — 1 ) = = lim ∆ x → 0 3 ( x + ∆ x ) 3 — 1 — 3 x 3 — 1 2 ∆ x · 3 ( x + ∆ x ) 3 — 1 + 3 x 3 — 1 = = lim ∆ x → 0 3 ( x + ∆ x ) 3 — 1 — ( 3 x 3 — 1 ) ∆ x · 3 ( x + ∆ x ) 3 — 1 + 3 x 3 — 1 = = 3 · lim ∆ x → 0 3 x 2 + 3 x ∆ x + ( ∆ x ) 2 3 ( x + ∆ x ) 3 — 1 + 3 x 3 — 1 = = 3 · 3 x 2 + 3 x · 0 + ( 0 ) 2 3 ( x + 0 ) 3 — 1 + 3 x 3 — 1 = 9 x 2 2 3 x 3 — 1

Ответ: 3 x 3 — 1 ‘ = 9 x 2 2 3 x 3 — 1 и x ∈ 1 3 3 ; + ∞

Для решения таких примеров необходимо учитывать то, что область определения функции f ( x ) может не совпадать с областью определения производной этой функции. Предыдущий пример имеет область определения вида D f x : x ∈ [ 1 3 3 ; + ∞ ) , а производная определена на интервале D f x : x ∈ 1 3 3 ; + ∞ . То есть при дифференцировании функция f ‘ ( x ) — это производная заданной функции f ( x ) из промежутка x ∈ D ( f ( x ) ) D ( f ‘ ( x ) ) .

Получение формул таблиц производных основано на определении производной. Они достаточно удобны, что способствует скорейшему дифференцированию сложных выражений. Использование понятия производной применяют для доказательств правил дифференцирования.

Определение, физический и геометрический смысл производной

п.1. Приращение аргумента и приращение функции

	\begin y=2x-1\\ x_0=1,\ x=1,1 \end Найдем приращение аргумента и функции. \begin \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=2\cdot 1,1-1=1,2\\ f(x_0 )=f(1)=2\cdot 1-1=1\\ \triangle y=f(x)-f(x_0 )=1,2-1=0,2\gt 0 \end
	\begin y=-x+2\\ x_0=1,\ x=1,1 \end Найдем приращение аргумента и функции. \begin \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=-1,1+2=0,9\\ f(x_0 )=f(1)=-1+2=1\\ \triangle y=f(x)-f(x_0)=0,9-1=-0,1\lt 0 \end

п.2. Определение производной

Например:
Найдем производную функции \(f(x)=x^2-4\) в точке \(x_0=3\)
Значение функции в точке: \(f(x_0 )=3^2-4=5\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда: \begin f(x)=f(x_0+\triangle x)=(x_0+\triangle x)^2-4=(3+\triangle x)^2-4=9+6\triangle x+\triangle x^2-4=\\ =5+6\triangle x+\triangle x^2 \end Приращение функции: $$ \triangle y=f(x)-f(x_0)=5+6\triangle x+\triangle x^2-5=6\triangle x+\triangle x^2=\triangle x(6+\triangle x) $$ Производная: $$ f'(x_0)=\lim_<\triangle x\rightarrow 0>\frac<\triangle x><\triangle y>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(6+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(6+\triangle x)=6+0=6 $$ Ответ: 6

п.3. Физический смысл производной

Рассмотрим прямолинейное движение.
Пусть расстояние по прямой между городами \(\triangle x=\) 300 км поезд преодолевает за \(\triangle t=\)4 часа. Мы легко можем найти его среднюю скорость: $$ v_=\frac<\triangle x><\triangle t>,\ \ v_=\frac<300><4>=75\ (\text<км/ч>) $$ Но поезд не едет все время с одной и той же скоростью: где-то ускоряется, где-то замедляется, где-то и вовсе останавливается.
Если мы захотим определить скорость как можно точнее, нам понадобится уменьшать интервалы времени и измерять соответствующий путь. Уменьшив время до «мгновений», мы получим «мгновенную скорость» для каждой точки траектории в каждый момент времени.

Сравнивая определения мгновенной скорости и производной функции, мы можем сформулировать физический смысл производной:

Или, ближе к физике/химии/биологии:

п.4. Геометрический смысл производной

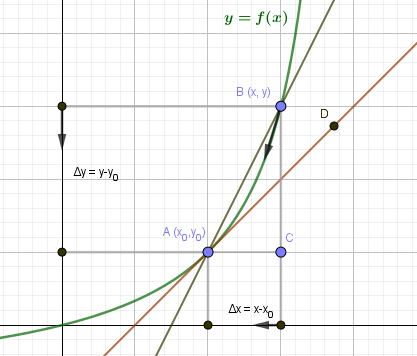
Пусть на плоскости задана кривая \(y=f(x)\).
Выберем на кривой две точки \(A(x_0,y_0)\) и \(B(x,y)\). Прямая AB будет секущей для кривой \(y=f(x)\). Угол наклона прямой AB определяется угловым коэффициентом: $$ k_=tg\angle A=\frac=\frac<\triangle y> <\triangle x>$$ Начнем движение точки B вдоль кривой по направлению к точке A. Приращение аргумента при этом будет уменьшаться: \(\triangle x=AC\rightarrow 0\). В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_=\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=y'(x_0) $$
Мы можем сформулировать геометрический смысл производной:

п.5. Алгоритм поиска значения производной в заданной точке

На входе: уравнение функции \(y=f(x)\), точка \(x_0\)
Шаг 1. Найти значение функции в заданной точке \(y_0=f(x_0)\).
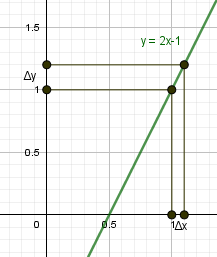
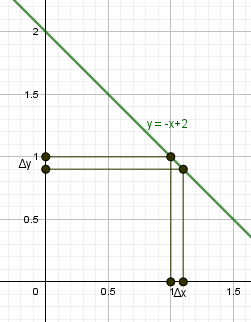
Шаг 2. Задать приращение аргумента \(\triangle x=x-x_0\), найти приращение функции \(\triangle y=f(x)-f(x_0)=f(x_0+\triangle x)-f(x_0)\).
Шаг 3. Найти предел \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=f'(x_0)\)
На выходе: значение производной в точке \(x_0\)

Например:
Найдем значение производной в точке \(x_0=1\) для функции \(y=x^2-3\).
Значение функции в заданной точке: \(f(x_0)=1^2-3=-2\)
Пусть \(∆x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=((1+\triangle x)^2-3)-(-2)=\\ =1+2\triangle x+(\triangle x)^2-1=2\triangle x+(\triangle x)^2=\triangle x(2+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2+\triangle x)=2+0=2 \end Искомая производная в заданной точке: \(f'(1)=2\)
Ответ: 2

п.6. Алгоритм поиска уравнения производной

На входе: уравнение функции \(y=f(x)\)
Шаг 1. Задать приращение аргумента \(\triangle x\), найти выражение для приращения функции \(\triangle y=f(x+\triangle x)-f(x)\).
Шаг 2. Найти предел выражения \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=f'(x)\)
На выходе: уравнение производной \(y\ ‘=f'(x)\) в любой точке \(x\).

Например:
Найдем общее уравнение производной для функции \(y=x^2-3\).
Пусть \(∆x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=((x+\triangle x)^2-3)-(x^2-3)=\\ =(x+\triangle x)^2-x^2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2x+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2x+\triangle x)=2x+0=2x \end Ответ: уравнение производной \(y\ ‘=2x\)

п.7. Примеры

Пример 1. Пользуясь алгоритмом поиска значения производной в заданной точке, найдите:
a) \( f'(1),\ \text<если>\ f(x)=2x \)
По условию \(x_0=1\)
Значение функции в заданной точке: \(f(x_0 )=2\cdot 1=2\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=2(1+\triangle x)-2=2+2\triangle x-2=2\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<2\triangle x><\triangle x>=2 \end Искомая производная в заданной точке: \(f'(1)=2\)
б) \( f'(3),\ \text<если>\ f(x)=3x^2 \)
По условию \(x_0=3\)
Значение функции в заданной точке: \(f(x_0 )=3\cdot 3^2=27\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=3(3+\triangle x)^2-27=3(9+6\triangle x+(\triangle x)^2)-27=\\ =27+18\triangle x+3(\triangle x)^2-27=3\triangle x(6+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<3\triangle x(6+\triangle x)><\triangle x>=3\lim_<\triangle x\rightarrow 0>(6+\triangle x)=3(6+0)=18 \end Искомая производная в заданной точке: \(f'(3)=18\)

в) \( f'(-1),\ \text<если>\ f(x)=4x-1 \)
По условию \(x_0=-1\)
Значение функции в заданной точке: \(f(x_0)=4\cdot (-1)-1=-5\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=(4(-1+\triangle x)-1)-(-5)=-5+4\triangle x+5=4\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<4\triangle x><\triangle x>=4 \end Искомая производная в заданной точке: \(f'(-1)=4\)

г) \( f'(2),\ \text<если>\ f(x)=x^3 \)
По условию \(x_0=2\)
Значение функции в заданной точке: \(f(x_0)=2^3=8\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x_0+\triangle x)-f(x_0)=(2+\triangle x)^3-8=\\ =2^3+3\cdot 2^2\cdot \triangle x+3\cdot 2\cdot (\triangle x)^2+(\triangle x)^3-8=\\ =12\triangle x+6(\triangle x)^2+(\triangle x)^3=\triangle x\cdot (12+6\triangle x+(\triangle x)^2 ) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x\cdot(12+6\triangle x+(\triangle x)^2)><\triangle x>=\lim_<\triangle x\rightarrow 0>(12+6\triangle x+(\triangle x)^2)=12+0+0=12 \end Искомая производная в заданной точке: \(f'(2)=12\)

Ответ: а) 2; б) 18; в) 4; г) 12

Пример 2. Пользуясь алгоритмом поиска уравнения производной, найдите общее уравнение производной для функции \(y=f(x)\):
a) \( f(x)=C\), где C – постоянная величина
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=C-C=0 \end Отношение \(\frac<\triangle y><\triangle x>=\frac<0><\triangle x>=0\)
Предел \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>0=0\)
Производная \(y\ ‘=C’=0\)

б) \( f(x)=x\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=x+\triangle x-x=\triangle x \end Ищем предел: \(\lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x><\triangle x>=\lim_<\triangle x\rightarrow 0>1=1\)
Производная \(x\ ‘=1\)

в) \( f(x)=x^2\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=(x+\triangle x)^2-x^2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x(2x+\triangle x)><\triangle x>=\lim_<\triangle x\rightarrow 0>(2x+\triangle x)=2x+0=2x \end Производная \((x^2)\ ‘=2x\)

г) \( f(x)=x^3\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=(x+\triangle x)^3-x^3=\\ =(x+\triangle x-x)((x+\triangle x)^2+x(x+\triangle x)+x^2)=\triangle x((x+\triangle x)^2+x(x+\triangle x)+x^2) \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x((x+\triangle x)^2+x(x+\triangle x)+x^2)><\triangle x>=\\ =\lim_<\triangle x\rightarrow 0>((x+\triangle x)^2+x(x+\triangle x)+x^2)=(x+0)^2+x(x+0)+x^2=3x^2 \end Производная \((x^3)\ ‘=3x^2\)

e) \( f(x)=kx+b\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin \triangle y=f(x+\triangle x)-f(x)=k(x+\triangle x)+b-kx-b=k\triangle x \end Ищем предел: \begin \lim_<\triangle x\rightarrow 0>\frac<\triangle y><\triangle x>=\lim_<\triangle x\rightarrow 0>\frac<\triangle x>=\lim_<\triangle x\rightarrow 0>k=k \end Производная \((kx+b)\ ‘=k\)