Численная схема для уравнения теплопроводности

Численные схемы решения двумерного уравнения теплопроводности в цилиндрических координатах Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Чермошенцева Алла Анатольевна, Плотникова Ирина Сабировна

Представлена математическая постановка задачи теплопроводности в цилиндрических координатах, описаны начальные и граничные условия. Обоснована необходимость для решения задачи использования численных методов. Рассмотрены различные разностные схемы и шаблоны, а также вопросы точности и сходимости.

Numeric schemes of solution of two-dimensional equation of thermal conductivity in cylindrival coordinates

Mathematical problem of heat transfer in cylindrical coordinates was presented. Initial and border conditions were described. The necessity of problem solving for using the numerical methods was proved. Various subtractive schemes , patterns, questions of accuracy and convergence were considered.

Текст научной работы на тему «Численные схемы решения двумерного уравнения теплопроводности в цилиндрических координатах»

ЧИСЛЕННЫЕ СХЕМЫ РЕШЕНИЯ ДВУМЕРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ

А.А. Чермошенцева1, И.С. Плотникова2

12Камчатский государственный технический университет, г. Петропавловск-Камчатский, 683003

e-mail: allachermoshentseva@mail. ru

Ключевые слова: двумерное уравнение теплопроводности, теплообмен скважины с окружающей породой, разностные схемы.

Numeric schemes of solution of two-dimensional equation of thermal conductivity in cylindrival coordinates. A.A. Chermoshentseva1, I.S. Plotnikova2 (u 2 Kamchatka State Technical University, Petropavlovsk-Kamchatskiy, Russia, 683003)

Mathematical problem of heat transfer in cylindrical coordinates was presented. Initial and border conditions were described. The necessity of problem solving for using the numerical methods was proved. Various subtractive schemes, patterns, questions of accuracy and convergence were considered.

Key words: two-dimensional equation of thermal conductivity, heat exchange of the well and surroundings, subtractive schemes.

Задача теплопроводности является одной из типичных нестационарных задач математической физики. Разведка и разработка геотермальных месторождений требует решения такой задачи при рассмотрении теплообмена скважины, окруженной практически неограниченным природным массивом горных пород, с потоком движущегося теплоносителя. Учитывая конструкцию скважины, целесообразно ввести цилиндрические координаты. Тогда для скважины с осесимметричным распределением температур, не имеющей внутренних источников теплоты, задача теплообмена с окружающей горной породой при моделировании пароводяного потока в стволе геотермальной скважины сводится к решению двумерной задачи теплопроводности [1, 2]:

о Т 1 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

уі*+1 Ц „І+1 «І . . 1 .1

Рис. 1 Шаблоны разностных схем: а — явная схема треугольника; б — схема Ричардсона; в — неявная схема треугольника; г, д — схема бегущего счета; е — схема Кранка — Николсона

Наибольшее распространение получила схема Кранка — Николсона, позволяющая по сравнению с неявной треугольной схемой выполнять примерно в 10 раз меньше вычислительной работы для расчетов на одном и том же временном интервале [8]. К тому же она имеет более хорошую аппроксимацию и является абсолютно устойчивой.

Обобщенная схема шеститочечного шаблона для двумерного случая принимает вид:

т’п т>п Л і Л Л.ТТ^+1 і 1 Т7^

—————= Л1+Л2 сТт п + 1 — ст Ттп ,

где Лг — разностный оператор:

1 т+1, п т, п т-1, п

2 т, п+1 т, п т, и-1

Температуру в узловой точке Ткт п сопровождают три индекса: т и п — индексы координат, к — индекс времени.

Чтобы определиться с тем, какую из схем следует использовать при решении конкретной задачи, необходимы оценки их точности, сходимости, устойчивости. Оценки точности схем

являются асимптотическими при стремлении шага к нулю, но даже быстродействующие современные ЭВМ не позволяют считать сложные реальные многомерные задачи с достаточно малым шагом. Если взять п интервалов по каждой из переменных, то сетка для р-мерной задачи будет содержать пР узлов. Реально может оказаться, что схема первого порядка точности на грубых сетках даст более точный результат, чем схема второго порядка точности, хотя на подробных сетках соотношение будет обратным. Обычно априорные оценки точности схем далеки от оптимальных и бывают завышены в десятки-сотни. Кроме того, не всякая сходящаяся разностная схема гарантирует получение качественного решения. Так, сходимость в гильбертовой норме (среднеквадратическая сходимость) обеспечивает передачу только некоторых интегральных характеристик решения, в чебышевской (сходимость в среднем) — обеспечивает хорошее качество решения только на подробной сетке, а на грубой сетке часто возникает так называемая разболтка, и результаты расчета получаются непригодными. Выбор метрического пространства фактически определяет класс функций, в которых следует искать решение. Чебышевская норма является более сильной, чем гильбертова, но ее использование не всегда удобно и во многих задачах необязательно. Для каждой конкретной задачи выбор пространств определяется в первую очередь физическим смыслом задачи, и только потом принимаются во внимание чисто математические соображения, такие, например, как возможность доказать сходимость. Так, в задачах о нагреве тела потоком тепла даже норма L\ удовлетворительна [8], поскольку температура тела определяется интегралом от потока по времени.

Рассмотрим существующие подходы к решению двумерных задач. В первом подходе время протекания процесса теплопроводности разбивают на последовательность интервалов Ат и проводят аппроксимацию производных искомых функций во времени, затем переходят к многомерной стационарной задаче относительно распределений этих функций в момент времени хк в конце каждого k-го интервала. Полученную в результате задачу можно решить приближенными аналитическими методами или численно.

Можно поступить наоборот (второй подход): ввести пространственную сетку и на ней аппроксимировать производные искомых функций по пространственным координатам. В результате получится система обыкновенных дифференциальных уравнений относительно меняющихся во времени узловых значений этих функций. Тогда задача сводится к задаче Коши.

Третий подход, объединяющий в себе первые два, связан с переходом к дискретной математической модели рассматриваемого процесса как в пространстве, так и во времени. Эта модель на каждом к-м интервале приводит к системе конечных уравнений относительно узловых значений искомых функций в момент времени хк в конце этого интервала.

1. Чермошенцева А.А. Течение теплоносителя в геотермальной скважине // Математическое моделирование. — 2006. — Т. 18, № 4. — С. 61-76.

2. Шулюпин А.Н, Чермошенцева А.А. Влияние теплообмена с окружающими породами на эксплуатационные параметры пароводяной скважины // Научный журнал КубГАУ. — Краснодар: КубГАУ, 2007. — № 23(03).

3. Лыков А.В. Теория теплопроводности. — М.: Высш. шк., 1967. — 599 с.

4. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров. — М.: Наука, 1964. — 608 с.

5. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. — М.: Энергоиздат, 1981. — 416 с.

6. Боглаев Ю.П. Вычислительная математика и программирование. — М.: Высш. шк., 1990. -543 с.

7. Власова Е.А., Зарубин В.С., Кувыркин Г.Н. Приближенные методы математической физики. — М.: Изд-во МГТУ им Н.Э. Баумана, 2001. — 700 с.

8. Калиткин Н.Н. Численные методы. — М.: Наука, 1978. — 512 с.

9. Лыков А.В. Тепломассообмен: Справочник. — М.: Энергия, 1978. — 479 с.

10. Марчук Г.И. Методы вычислительной математики. — М.: Наука, 1980. — 536 с.

11. Самарский А.А. Теория разностных схем. — М.: Наука, 1989. — 614 с.

12. Самарский А.А., Гулин А.В. Устойчивость разностных схем. — М.: Наука, 1973. — 415 с.

13. Самарский А.А., Гулин А.В. Численные методы. — М.: Наука, 1989. — 429 с.

14. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. — М.: Наука, 1992. — 422 с.

15. Созинова Т.Е. Разработка метода расчета и исследования теплового и термонапряженного состояния крепи геотермальных скважин: Автореф. дис . канд. тех. наук. — Иваново, 1997. — 24 с.

16. Тихонов А.Н., Самарский А.А. Уравнения математической физики. — М.: Наука, 1966. — 724 с.

17. Чермошенцева А.А. Численные методы: Учеб. пособие. (ДВ РУМЦ). — Петропавловск-Камчатский, Изд-во КамчатГТУ, 2008. — 110 с.

Уравнение теплопроводности в tensorflow

Привет, Хабр! Некоторое время назад увлекся глубоким обучением и стал потихоньку изучать tensorflow. Пока копался в tensorflow вспомнил про свою курсовую по параллельному программированию, которую делал в том году на 4 курсе университета. Задание там формулировалось так:

Линейная начально-краевая задача для двумерного уравнения теплопроводности:

Хотя правильнее было бы назвать это уравнением диффузии.

Задачу тогда требовалось решить методом конечных разностей по неявной схеме, используя MPI для распараллеливания и метод сопряженных градиентов.

Я не специалист в численных методах, пока не специалист в tensorflow, но опыт у меня уже появился. И я загорелся желанием попробовать вычислять урматы на фреймворке для глубокого обучения. Метод сопряженных градиентов реализовывать второй раз уже не интересно, зато интересно посмотреть как с вычислением справится tensorflow и какие сложности при этом возникнут. Этот пост про то, что из этого вышло.

Численный алгоритм

Разностная схема:

Чтобы проще было расписывать, введем операторы:

Явная разностная схема:

В случае явной разностной схемы для вычисления используются значения функции в предыдущий момент времени и не требуется решать уравнение на значения . Однако такая схема менее точная и требует значительно меньший шаг по времени.

Неявная разностная схема:

Перенесем в левую сторону все связанное с , а в правую и домножим на :

По сути мы получили операторное уравнение над сеткой:

что, если записать значения в узлах сетки как обычный вектор, является обычной системой линейных уравнений (). Значения в предыдущий момент времени константы, так как уже рассчитаны.
Для удобства представим оператор как разность двух операторов:

Заменив на нашу оценку , запишем функционал ошибки:

где — ошибка в узлах сетки.

Будем итерационно минимизировать функционал ошибки, используя градиент.

В итоге задача свелась к перемножению тензоров и градиентному спуску, а это именно то, для чего tensorflow и был задуман.

Реализация на tensorflow

Кратко о tensorflow

В tensorflow сначала строится граф вычислений. Ресурсы под граф выделяются внутри tf.Session. Узлы графа — это операции над данными. Ячейками для входных данных в граф служат tf.placeholder. Чтобы выполнить граф, надо у объекта сессии запустить метод run, передав в него интересующую операцию и входные данные для плейсхолдеров. Метод run вернет результат выполнения операции, а также может изменить значения внутри tf.Variable в рамках сессии.

tensorflow сам умеет строить графы операций, реализующие backpropagation градиента, при условии, что в оригинальном графе присутствуют только операции, для которых реализован градиент (пока не у всех).

Сначала код инициализации. Здесь производим все предварительные операции и считаем все, что можно посчитать заранее.

По-хорошему надо было считать значения функции на краях заданными и оптимизировать значения функции только во внутренней области, но с этим возникли проблемы. Способа сделать оптимизируемым только часть тензора не нашлось, и у операции присвоения значения срезу тензора не написан градиент (на момент написания поста). Можно было бы попробовать хитро повозиться на краях или написать свой оптимизатор. Но и просто добавление разности на краях значений функции и краевых условий в функционал ошибки хорошо работает.

Стоит отметить, что метод с адаптивным моментом показал себя наилучшим образом, пусть функционал ошибки и квадратичный.

Вычисление функции: в каждый момент времени делаем несколько оптимизационных итераций, пока не превысим maxiter или ошибка не станет меньше eps, сохраняем и переходим к следующему моменту.

Запуск:

Результаты

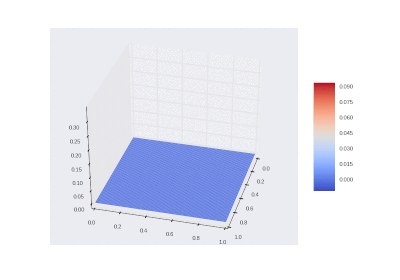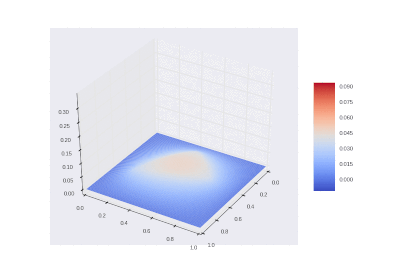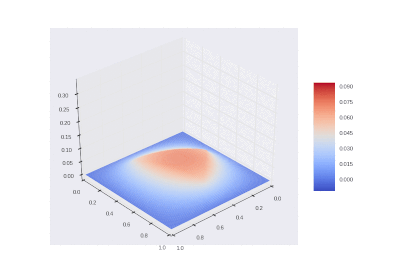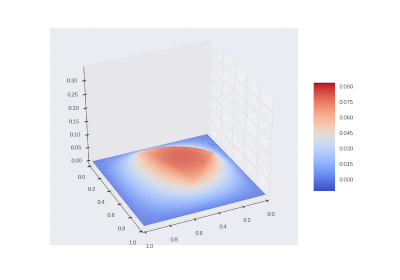
Условие как и оригинальное, но без в уравнении:

Что легко правится в коде:

Разницы почти нет, потому что производные имеют большие порядки, чем сама функция.

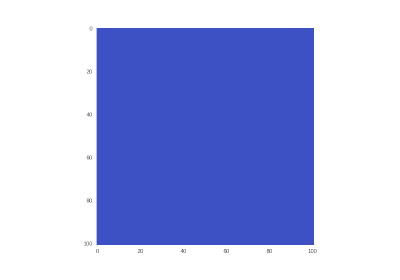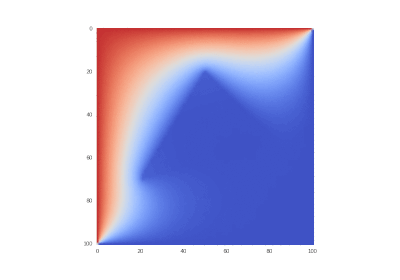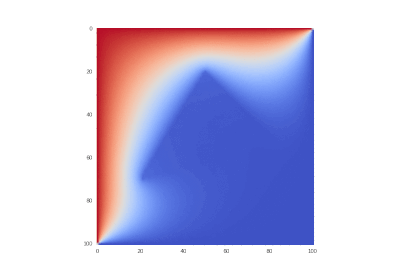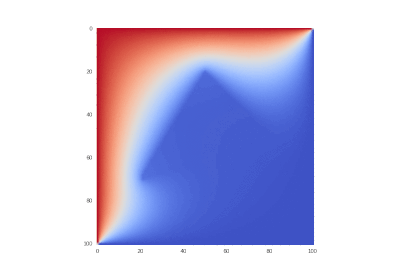
Условие с одним нагревающимся краем:

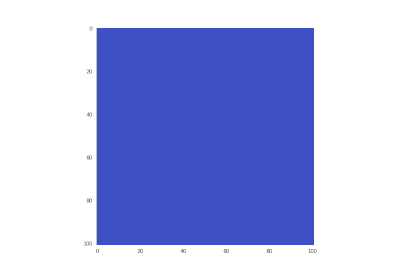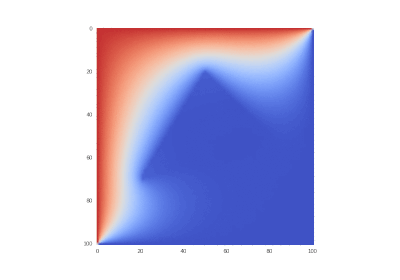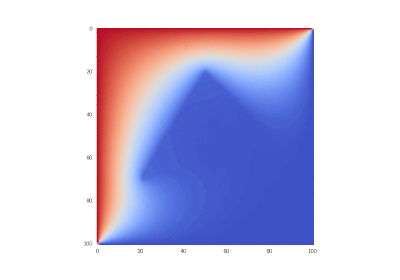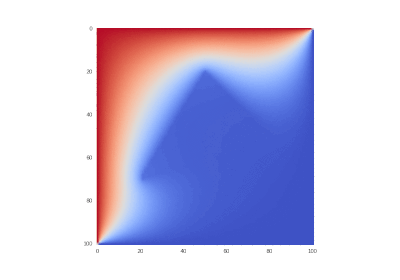
Условие с остыванием изначально нагретой области:

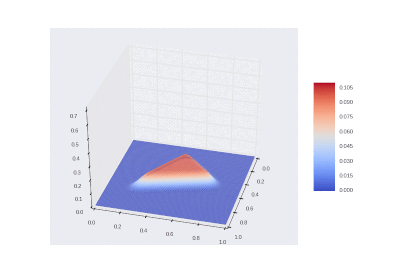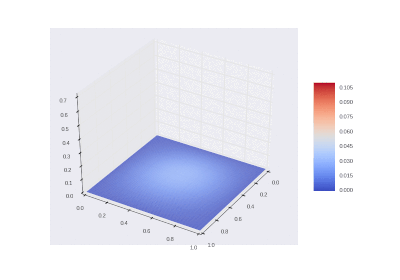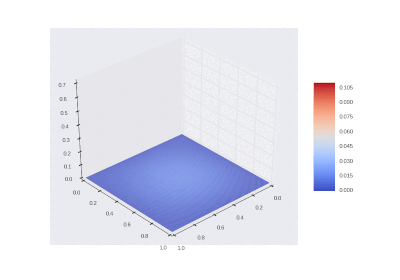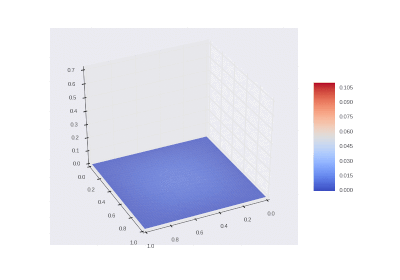
Условие с включением нагрева в области:

Рисование гифок

Функция рисования 3D-гифки:

В основной класс добавляем метод, возвращающий U в виде pandas.DataFrame

Функция рисования 2D-гифки:

Стоит отметить, что оригинальное условие без использования GPU считалось 4м 26с, а с использованием GPU 2м 11с. При больших значениях точек разрыв растет. Однако не все операции в полученном графе GPU-совместимы.

Intel Core i7 6700HQ 2600 МГц,
NVIDIA GeForce GTX 960M.

Посмотреть, какие операции на чем выполняются, можно с помощью следующего кода:

Это был интересный опыт. Tensorflow неплохо показал себя для этой задачи. Может быть даже такой подход получит какое-то применение — всяко приятнее писать код на питоне, чем на C/C++, а с развитием tensorflow станет еще проще.

источники:

http://habr.com/ru/post/321734/