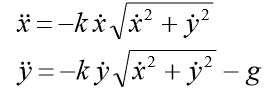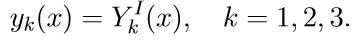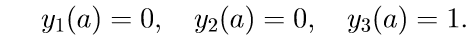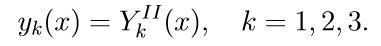Численное решение систем дифференциальных уравнений методом эйлера
Системой дифференциальных уравнений называется система вида
где x — независимый аргумент,
yi — зависимая функция, 
Функции yi(x), при подстановке которой система уравнений обращается в тождество, называется решением системой дифференциальных уравнений.
Численные методы решения систем дифференциальных уравнений.
Модифицированный метод Эйлера.
Метод Рунге-Кутта четвертого порядка.
Дифференциальным уравнением второго порядка называется уравнение вида
| F(x,y,у’,y»)=0 | (1) |
| y»=f(x,y,y’). | (2) |
Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.
Численно ищется частное решение уравнения (2), которое удовлетворяет заданным начальным условиям, то есть решается задача Коши.
Для численного решения дифференциальное уравнение второго порядка преобразуется в систему двух дифференциальных уравнений первого порядка и приводится к машинному виду (3). Для этого вводится новая неизвестная функция 
 . . | (3) |
Функция f2(x, y1, y) в систему (3) введена формально для того, чтобы методы, которые будут показаны ниже, могли быть использованы для решения произвольной системы дифференциальных уравнений первого порядка. Рассмотрим несколько численных методов решения системы (3). Расчетные зависимости для i+1 шага интегрирования имеют следующий вид. Для решения системы из n уравнений расчетные формулы приведены выше. Для решения системы из двух уравнений расчетные формулы удобно записать без двойных индексов в следующем виде:
Метод Рунге-Кутта четвертого порядка.
где h — шаг интегрирования. Начальные условия при численном интегрировании учитываются на нулевом шаге: i=0, x=x0, y1=y10, y=y0.
Контрольное задание по зачетной работе.
Колебания с одной степенью свободы
Цель. Изучение численных методов решения дифференциальных уравнений второго порядка и систем дифференциальных уравнений первого порядка.
Задание. Численно и аналитически найти:
- закон движения материальной точки на пружинке х(t),
- закон изменения силы тока I(t) в колебательном контуре (RLC — цепи) для заданных в табл.1,2 режимов. Построить графики искомых функций.
Свободные незатухающие колебания
Затухающее колебательное движение
Предельное апериодическое движение
Вынужденное колебание без сопротивления
Вынужденное колебание без сопротивления, явление резонанса
Вынужденное колебание с линейным сопротивлением
Вынужденное колебание с линейным сопротивлением, явление резонанса
Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений
Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ \begin
Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ \begin
Численные методы решения задачи Коши
Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
Идея численных методов решения задачи (3), (4) состоит из четырех частей:
1. Вводится расчетная сетка по переменной \( t \) (время) из \( N_t + 1 \) точки \( t_0 \), \( t_1 \), \( \ldots \), \( t_
2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.
3. Аппроксимируем производные конечными разностями.
4. Формулируем алгоритм, который вычисляет новые значения \( \pmb
Явный метод Эйлера
Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами \( t_n \) и \( t_
Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ \pmb^\prime (t_n) = \pmb
Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ \pmb^\prime(t) = \lim_ <\tau \to 0>\frac<\pmb(t+\tau) — \pmb(t)><\tau>. $$
В произвольном узле сетки \( t_n \) это определение можно переписать в виде: $$ \begin
Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение \( y^n \) для того, чтобы решить уравнение (5) относительно \( y^
При условии, что у нас известно начальное значение \( \pmb
Программная реализация явного метода Эйлера
Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом
При решении системы (векторный случай), u[n] — одномерный массив numpy длины \( m+1 \) (\( m \) — размерность задачи), а функция F должна возвращать numpy -массив размерности \( m+1 \), t[n] — значение в момент времени \( t_n \).
Таким образом численное решение на отрезке \( [0, T] \) должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.
Функция euler решения системы уравнений реализована в файле euler.py:
Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .
Неявный метод Эйлера
При построении неявного метода Эйлера значение функции \( F \) берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ \begin
Таким образом для нахождения приближенного значения искомой функции на новом временном слое \( t_
Для решения уравнения (8) можно использовать, например, метод Ньютона.
Программная реализация неявного метода Эйлера
Функция backward_euler решения системы уравнений реализована в файле euler.py:
Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .
Методы Рунге—Кутта
Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ \begin
Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ \begin
Многошаговые методы
В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах \( \pmb
Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ \begin
Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции \( \pmb
Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен \( m+1 \).
Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям \( \pmb
Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет \( m \)-ый порядок.
На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ \frac<\pmb
Жесткие системы ОДУ
При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке \( u = w \) передаются линейной системой $$ \begin
Пусть \( \lambda_i(t) \), \( i = 1, 2, \ldots, m \) — собственные числа матрицы $$ \begin
Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование \( A \)-устойчивых или \( A(\alpha) \)-устойчивых методов.
Метод называется \( A \)-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ \begin
Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
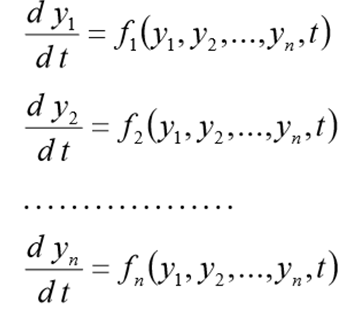
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши


по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 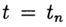

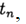


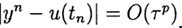


При 
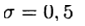
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
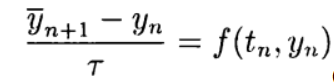
а на этапе корректора (уточнения) — схема
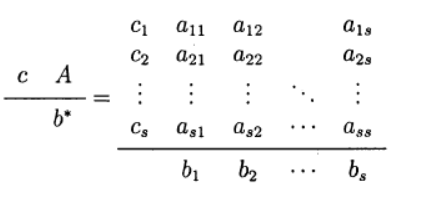
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
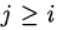

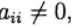
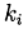
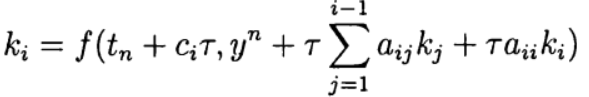
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 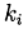
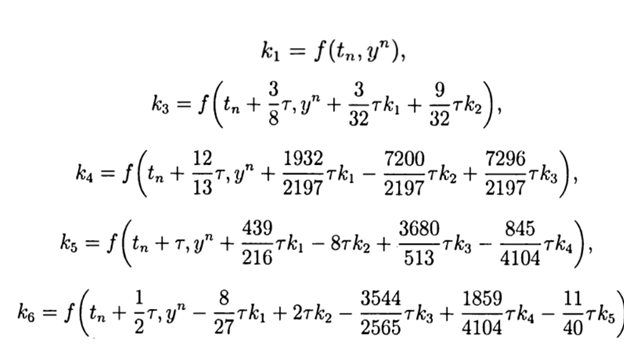
С учётом(9) общее решение имеет вид:
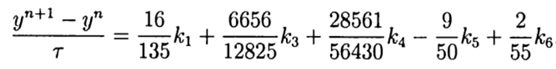
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
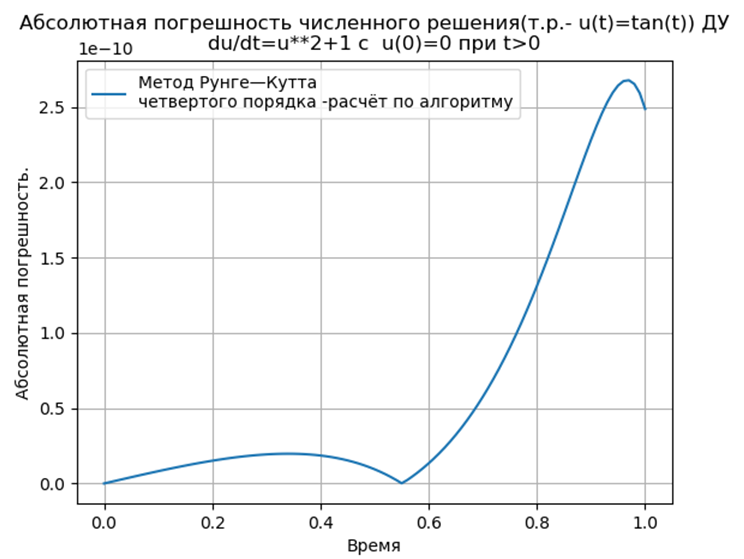
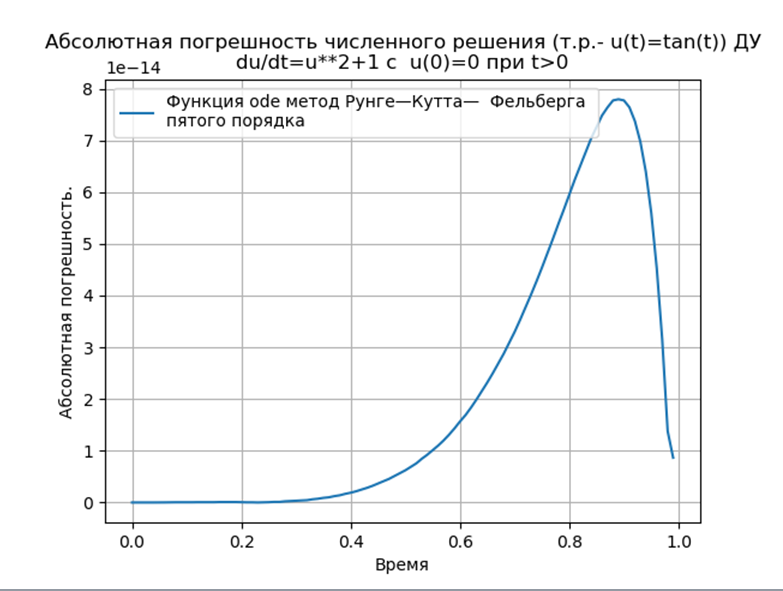
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
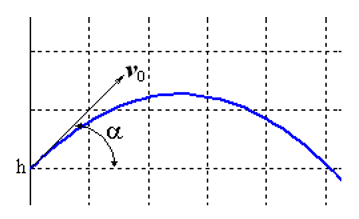
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 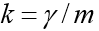
К системе следует добавить начальные условия: 

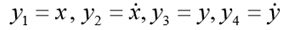
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
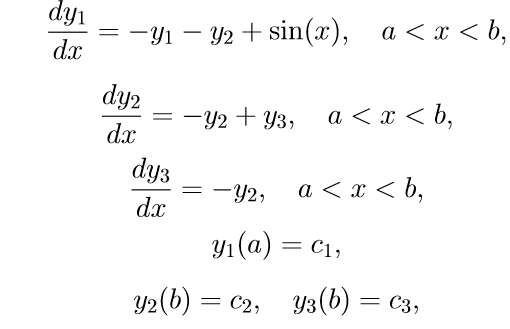
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 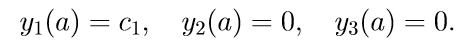
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 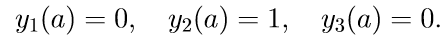
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 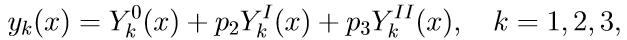
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
http://slemeshevsky.github.io/num-mmf/ode/html/._ode-FlatUI001.html
http://habr.com/ru/post/418139/

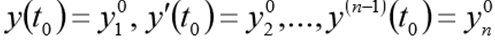


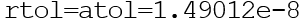
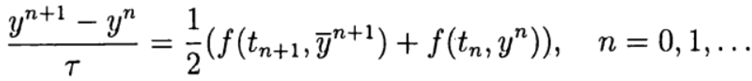
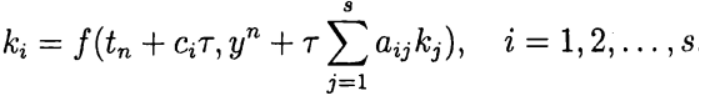
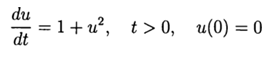 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга