Численное решение стационарного уравнения теплопроводности

Метод Finite Volume — реализация на примере теплопроводности

Метод Finite Volume (FVM)

В основе метода лежит разбиение области на непересекающиеся контрольные объемы(элементы), узловые точки, в которых ищется решение.Узловые точки находятся в центрах контрольных объемов.Также, как и для метода конечных разностей, для каждого элемента составляется уравнение, получается система линейных уравнений.Решая ее — находим значения
искомых переменных в узловых точках.Для отдельного элемента уравнение получается путем интегрирования исходного дифф уравнения по элементу и аппроксимации интегралов.

Термин конечный объем в статье будет часто заменятся на Элемент, будем для удобства считать их эквивалентами (элемент в данной статье не имеет ничего общего с методом конечных элементов).

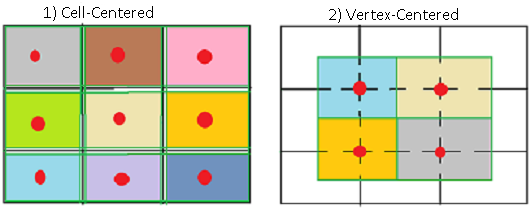
Есть 2 различных способа решения задачи по FVM:
1) грани контрольного объема совпадают с гранями элемента
2) грани контрольного объема проходят через центры граней элементов(на которые разбита область).Искомые переменные хранятся в вершинах этих элементов.Вокруг каждой вершины строится контрольный объем. Для непрямоугольной сетки этот способ имеет еще 2 подвида.

Мы будем использовать способ 1) с контрольными объемами совпадающими с элементами на которые разбита область.

Некоторые плюсы FVM:

• сохранение основных величин по всей области, таких как энергия системы, масса, тепловые потоки и тд.Причом это условие выполняется даже для грубой расчетной сетки
• высокая скорость расчета.Многие расчетные величины можно вычислить при разбиении области на элементы, и вычислять их на каждом шаге по времени нет необходимости.
• легкость использования для задач со сложной геометрией и криволинейными границами.Легкость использования разных геометрических типов элементов — треугольники, полигоны.

Метод FVM реализуем на примере уравнения теплопроводности:

Итак основные шаги при реализации FVM:

1. Перевод дифф уравнения в форму пригодную для FVM — интегрирование по контрольному объему
2. Составление дискретного аналога, выбор способа перевода производных и других подынтегральных выражений в дискретную форму
3. Получение уравнения для каждого из контрольных объемов, на которые разбита область.Составление системы линейных уравнений и ее решение.

Дискретизация по времени.

Немного теории или первый шаг в реализации FVM

FVM на стандартной прямоугольной сетке

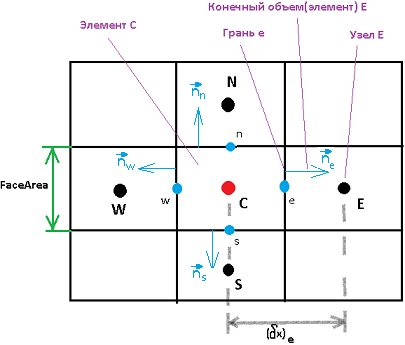
На рисунке изображен Элемент С и его соседние элементы справа(E), слева(W), сверху(N) и снизу(S).У элемента С есть 4 грани обозначенные буквами e w n s.Именно эти 4 грани и составляют периметр элемента и по ним производится интегрирование.Для каждого элемента в результате получаем дискретный аналог исходного дифф уравнения.

Составим дискретный аналог для элемента С.Для начала нужно разобраться с интегралом (3).Интеграл это ведь по факту сумма.Поэтому мы и заменяем интеграл по всей поверхности элемента, на сумму по 4-м составляющим этой поверхности, тоесть 4 граням элемента.

Уравнение (7) и есть конечное уравнение для элемента С, из него мы на каждом шаге по времени получаем новое значение температуры (Tnew) в элементе С.

Граничные условия на прямоугольной сетке

Мы рассмотрим только 2 вида граничных условий.

1. Задана температура Tb на границе
2. Задан поток FluxB на границе, рассмотрим только случай когда FluxB=0, т.е. грань e будет теплоизолирована(Insulated)

Случай 2) самый простой, поскольку получается что грань e не потребуется при дискретизации(т.к. все коэффициенты Flux=0) и можно ее просто пропустить.

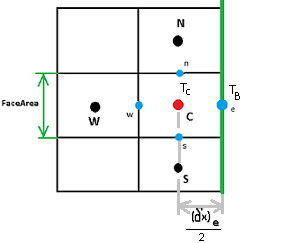
Теперь рассмотрим случай 1).Дискретизация грани e будет в целом похожа на ту что уже была описана.Будут только 2 изменения — вместо Te будет известное граничное значение Tb и вместо расстояния DXe будет DXe/2.В остальном можно рассматривать значение Te так, как будто это был бы обычный соседний узел E.Теперь подробнее распишем терм для граничного элемента С.

Пример численных расчетов на прямоугольной сетке

FVM в задачах со сложной геометрией

Здесь как раз проявляется преимущество FVM, где также, как и в методе конечных элементов, можно представлять область с круглыми границами через разбиение на треугольники или любые другие полигоны.Но FVM имеет еще 1 плюс — при переходе от треугольников к полигонам с большим числом сторон не требуется абсолютно ничего менять, конечно если код был написан для произвольного треугольника а не равностороннего.Более того, можно без изменения кода использовать смесь разных элементов — треугольники, полигоны, квадраты и тд.

Рассмотрим общий случай, когда вектор соединяющий центры 2-х элементов не совпадает с вектором нормали к общей грани этих элементов.Вычисление потока flux через грань теперь будет состоять из 2-х частей.В первой будет расcчитываться ортогональная составляющая а во второй так называемая «кросс-диффузия».

На картинке изображены 2 элемента, С — текущий рассматриваемый элемент и F — соседний элемент.Опишем дискретизацию для грани, разделяющей эти 2 элемента.Вектор соединяющий центры элементов — DCF.Вектор e — это единичный вектор по направлению DCF.Вектор Sf — направлен по нормали к грани, его длинна равна длине грани.

В исходниках я не стал реализовывать терм с кроссдиффузией, т.к встал вопрос — как проверить корректность такой реализации.Визуально сравнение результатов Матлаб и моих ничем не отличалось в отсутствии кросс-диффузии.Видимо это связано с тем что Матлаб любит треугольники близкие к равносторонним, что в итоге делает кроссдиффузию=0.Возможно позже еще вернусь к этому вопросу.

Расчет граничных элементов ничем не отличается от расчетов не на границе, вместо центра соседнего элемента берется центр грани, ну и как обычно подставляется температура на границе.
В моей реализации в итоге получается так:

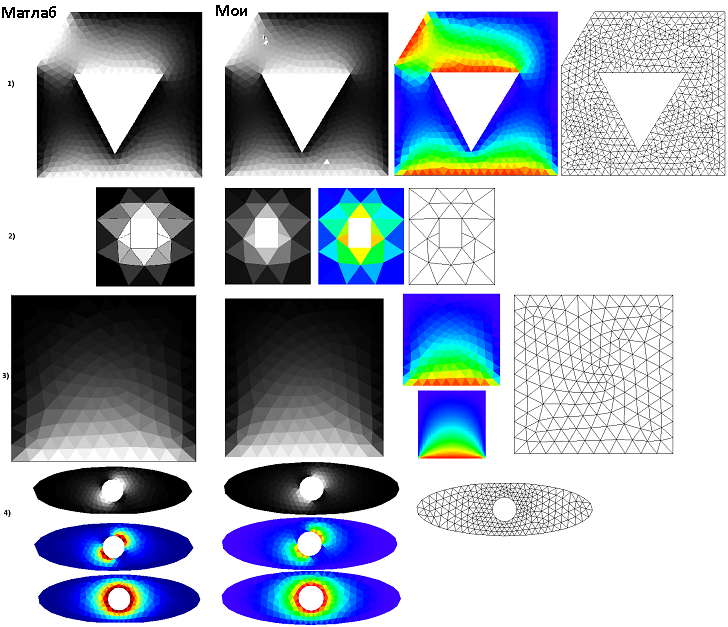
Примеры и проверка результатов

Описание структуры исходников

Гитхаб с исходниками лежит тут
Основная версия в папке heat2PolyV2.То что относится к вычислительной части лежит в heat2PolyV2\Src\FiniteVolume\.

Вначале файла Scene2.cs — параметры которые можно менять для отображения в разных цветовых схемах, масштаб, отображение mesh и т.д.Сами примеры хранятся в heat2PolyV2\bin\Debug\Demos\
Выгрузку из Матлаба сделать просто — нужно открыть pde toolbox, открыть m файл (либо создать самому с нуля), зайти в меню Mesh-Экспорт mesh, нажать ОК; перейти в основной Матлаб, в панельке появятся переменные — матрицы p e t, открыть файл savemymesh.m, выполнить его, появится файл p.out, перенести его в папку Demos.
В исходниках для выбора примера необходимо задать имя файла в строке param.file = «p»;(FormParam.cs).Далее необходимо применить граничные условия — для готовых примеров можно просто раскомментировать соответствующие блоки в MainSolver.cs:

Смысл тут простой — Матлаб разделяет границы по доменам, например внешние и внутренние.Также для каждого домена границы разбиты на части (группы), чтобы можно было задавать условия на участках границы по отдельности — например справа или снизу.
Возможно и вовсе не использовать Матлаб, а вручную прописать все элементы(треугольники) и их вершины + грани(только для граничных элементов)

Методы решения УЧП

МЕТОДЫ РЕШЕНИЯ УЧП

1. Уравнение теплопроводности

Рассмотрим численное решение уравнений с частными производными (УЧП) на примере решения уравнения теплопроводности (диффузии)

— плотность тепловых источников, — коэффициент теплопроводности

Если , то мы имеем стационарное уравнение теплопроводности

— уравнение Пуассона.

Если плотность тепловых источников тоже равна 0, то получаемое уравнение называется уравнением Лапласа.

Стационарное уравнение теплопроводности может быть решено, если известны граничные условия.

Это могут быть или значения искомой функции на границе (задача Дирихле).

Или значения потока тепла на границе (задача Неймана)

Либо смешанные условия.

Если необходимо решать УЧП в области, имеющей круговую симметрию, оператор Лапласа удобна записать в полярных координатах:

2. РЕШЕНИЕ СТАЦИОНАРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

Будем решать задачу Дирихле для уравнения Пуассона.

в прямоугольной области , .

Для численного решения данной задачи применим метод SOR (метод последовательной верхней релаксации). Вначале используем метод конечных разностей. Для этого разобьем отрезок [a, b] на K равных интервалов длиной , а отрезок [c, d] — на L интервалов той же длины. Пусть при этом , . Тогда

Таким образом, мы разбили весь прямоугольник , на квадраты со стороной ,получив при этом сетку (решетку). Будем искать нужную нам функцию в узлах этой решетки методом конечных разностей. То есть будем искать эту функцию в виде матрицы

Запишем вначале в одномерном случае рамках метода конечных разностей производную функции U по х в точке . Получим

Для второй производной в точке получим

Аналогичным образом, для второй производной в точке имеем

Перейдем теперь к двумерной области и найдем вторые производные в точке , .

,

Подставив полученные таким образом вторые производные в уравнение Пуассона, имеем

Коэффициенты перед матричными элементами в данном случае равны 1 и 4. Однако в общем случае (полярные координаты, например) мы должны записать

и вычислить A, B, C, D, E.

Перепишем полученное нами уравнение в следующем виде:

Разность между левой и правой частями уравнения называется невязкой

Подставляя в правую часть (3) уравнение (1) имеем

Уравнение (4) является тождеством. Его можно использовать в случае, когда решение ищется методом последовательных приближений

Это и есть основное уравнение метода SOR. Параметр обычно выбирается не тождественно равным 1, изменяющимся параметром от 1 до 1.5. Это делается для лучшей сходимости метода. В качестве начального приближения берется функция, тождественно равная 0 внутри области определения и равная граничным условиям на границе области.

3. РЕШЕНИЕ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

Будем искать решение этой задачи методом Кранка-Николсона. Рассмотрим вначале одномерное нестационарное уравнение диффузии.

Запишем производную по времени в k-й точке х в n-й момент времени в виде:

Здесь — шаг по времени. В правой части вторую производную по координате можно взять как в момент времени ,

так и в момент времени

Суть метода Кранка-Николсона заключается в том, что производная в правой части берется как среднее арифметическое от производных в точках и . То есть

Для двумерного уравнения диффузии

в рамках метода Кранка-Николсона запишем вторые производные по х и по у

как среднее арифметическое от производных в точках и ,

перенесем все значения функции в момент времени влево, а в — й вправо. Получим.

,

(1)

(2)

Схема расчета по методу Кранка-Николсона такова:

1. В начальный момент времени из начальных и граничных условий методом SOR (или каким-либо другим методом) находим значения функции U.

2. Вычисляем с ее помощью в этот же момент времени по формуле (2) функцию F.

3. По формуле (1) с помощью уже вычисленной функции F и граничных условий находим значение функции U в следующий момент времени.

4. Вычисляем с ее помощью по формуле (2) функцию F.

5. По формуле (1) находим значение функции U в следующий момент времени.

МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

4. Решение одномерного уравнения теплопроводности

Базисные функции метода конечных элементов

Суть метода в том, что искомая функция ищется интерполяцией с помощью базисных функций. В этом случае отпадает необходимость расчета производных методом конечных разностей.

Пусть отрезок [a, b], на котором определяется искомая функция, разбит N точками на (N-1) равных отрезков (конечных элементов) длиной . На рисунке показан случай, когда N = 4.

Значения функции в этих точках равны , , . , . на каждом из конечных элементов функцию u(x) можно представить с помощью базисных функций :