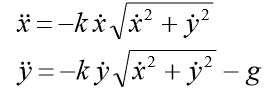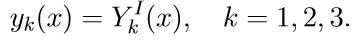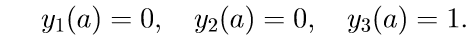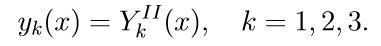Анализ явных численных методов решения стохастических дифференциальных уравнений
Вычислительный центр им. РАН,
Свентокшиская Академия в Кельцах, Польша
АНАЛИЗ ЯВНЫХ ЧИСЛЕННЫХ МЕТОДОВ
Рассматриваются основные принципы построения численных методов решения стохастических дифференциальных уравнений (СДУ). Анализируется проблема жесткости систем СДУ. Для одномерного СДУ Ито сравнивается точность аппроксимации существующих явных численных методов.
Анализ и синтез стохастических динамических систем часто связан с использованием численного решения СДУ. Для ряда задач таких, как фильтрация, идентификация, прогнозирование и оптимальное управление, интегрирование численного решения СДУ должно выполняться в реальном времени и, кроме того, с определенной точностью и устойчивостью. В связи с этим возникает ряд проблем. С одной стороны, очень не многие СДУ имеют аналитические решения (в основном это – линейные СДУ с аддитивным или мультипликативным шумом или нелинейные СДУ, сводимые к линейным [1]), а с другой – физические особенности реальных динамических систем [2] приводят к проявлению жесткости, что неудовлетворительно влияет на получаемое численное решение. Поэтому особо важным этапов при проектировании стохастической динамической системы является выбор схемы численного решения СДУ.
2. Принципы построения численных методов решения
стохастических дифференциальных уравнений
В настоящее время существует несколько подходов создания численных схем решения СДУ. Одной из возможностей является адаптация существующих для обыкновенных дифференциальных схем (ОДУ) схем с учетом свойств стохастических интегралов, другой – разработка специальных методов решения СДУ [3]. Большинство исследователей использует первый подход, поскольку теория численного решения ОДУ хорошо разработана и достаточно легко можно провести аналогии между ОДУ и СДУ.
Самым простым методом аппроксимации численного решения СДУ (с вычислительной точки зрения) является метод Эйлера, разработанный Маруямой в 1955г [3]. Эта схема удовлетворяет многим необходимым свойствам, предъявляемым к численным методам (она имеет порядок сходимости 
По аналогии с разработкой схем численного решения ОДУ для повышения порядка сходимости, точности аппроксимации и устойчивости можно использовать разложение в ряд в точке аппроксимации, т. е. использования производных различных порядков, как переменной, так и коэффициентов дрейфа и диффузии. В литературе этот подход получил название метода Тейлора [3]. Однако недостатком схем Тейлора является то, что на каждом шаге аппроксимации требуется вычислять кратные стохастические интегралы, связанные с вышеуказанными производными. Для того, чтобы избежать вычислительные трудности можно использовать многократное деление шага аппроксимации (методы Рунге-Кутта [4]) или результаты аппроксимации предыдущих шагов (многошаговые методы [5 – 7]).
Как обыкновенные, так и стохастические системы дифференциальных уравнений, описывающие многие физические, биологические или экономические явления, при компьютерном моделировании с использованием обычных численных схем демонстрируют «нежелательное» поведение и могут быть отнесены к классу некорректных задач. В большинстве случаев под «нежелательным» поведением понимается очень высокая нестабильность численного решения, связанная с так называемым явлением жесткости. Существует несколько возможных объяснений этого явления.
Первая причина ассоциируется с техническими возможностями компьютера. Так для достижения желаемой точности можно применить многократное деление шага интегрирования. С одной стороны, это приводит к накоплению ошибки округления, и как следствие, возникает переполнение регистров компьютера. С другой стороны использование очень малых значений шага интегрирования требует огромных ресурсов времени и также приводит к накоплению ошибки округления. Вторая причина связана с физической стороной рассматриваемой системы. Это означает, что система описывает процессы различных скоростей или градиентов (прежде всего это характерно для некорректных задач). Такое явление обычно выступает в задачах пограничного слоя (гидродинамика), скин-эффекта (электромагнетизм), реакции химической кинетики и т. п. Наконец, жесткость может быть вызвана обеими причинами. Поэтому при разработке стабильных численных методов требуется учитывать вышеуказанные ситуации.
Анализ современной литературы показал, что создание численных методов решения жестких систем в большинстве случаев основано на идеях, представленных Хайрером и Ваннером [8]. В своей работе они постулировали, что жесткие системы не могут быть решены явными методами, и представили подходы, основанные только на использовании неявных методов. Однако следует отметить, что непосредственное применение этих методов всегда связано с крайне сложной процедурой определения параметров схемы, основанной на заранее выделенной области устойчивости только для рассматриваемой системы. Это обстоятельство делает предложенные подходы не приемлемыми для большинства вышеуказанных приложений, но позволяет выделить два важных математических свойства жесткости. Во-первых, все жесткие системы обладают очень широким спектром (или присутствием очень разных экспонент Ляпунова). Во-вторых, согласно теореме единственности и существования решения, для жестких систем характерны большие значения константы Липшица.
Итак, анализ принципов создания численных схем решения СДУ показал необходимость тщательного исследования существующих и, возможно, поиска новых методов, при решении конкретных задач.
3. Явные сильные численные схемы
Запишем СДУ в представлении Ито в общем виде


где 










Получение сильного решения СДУ (3.1) является важным моментом во многих практических задачах, целью работы является сравнительный анализ существующих сильных явных численных методов решения СДУ.
Рассмотрим наиболее распространенный в финансовой литературе случай [9, 10] – случай одномерного уравнения (3.1), используя схемы: Эйлера, Мильштейна, Тейлора, Рунге-Кутта и двухшаговую [3]. В одномерном случае схема Эйлера имеет вид:

где 


Схема Мильштейна, обладающая порядком сильной сходимости 

схема Тейлора порядка 

а двухшаговая схема порядка 

Схема Рунге-Кутта, где порядок сходимости 






4. Сравнение схем по критерию абсолютной ошибки
Оценка качества аппроксимации той или иной численной схемы обычно связана с главной целью проводимого исследования или интерпретацией получаемого решения. Поскольку решение СДУ может быть решением в сильном или слабом смысле, то введение критерия качества аппроксимации должно учитывать этот факт. В работе рассматривается случай сильного решения СДУ, поэтому в такого критерия можно использовать критерий «абсолютной ошибки» или математическое ожидание абсолютного значения меры близости между результатом аппроксимации 



где 
Заменим теоретическое значение критерия «абсолютной ошибки» (4.1) его статистическим аналогом, основываясь на моделировании Монте-Карло. Для этого предположим, что имеются по 




Сравним вышеописанные схемы по критерию абсолютной ошибки. В качестве первого тестового примера исследуем линейное СДУ с постоянными однородными коэффициентами

аналитическое решение которого имеет вид

Вторым тестовым примером является нелинейное СДУ Ито вида
с дифференцируемой функцией 


В частности, для уравнения

аналитическое решение есть

Выполним вычислительные эксперименты с использованием компьютера типа IBM PC с процессором AMD Athlon (TM) XP 3000+ для тестовых уравнений (4.3) и (4.4), используя численные схемы (3.2) – (3.6) и исследуя зависимость между длиной шага интегрирования 

Для первого и второго тестовых уравнений (см. табл.1 и табл.2) при уменьшении длины шага интегрирования и увеличении порядка сходимости численной схемы возрастает точность аппроксимации для всех исследуемых численных схем.
Однако этого нельзя утверждать в третьем случае, который представлял жесткое СДУ [11] (см. табл.3). Удалось рассчитать значение абсолютной ошибки для всех комбинаций длины шага интегрирования и количества траекторий только для схемы Эйлера и двухшаговой схемы.
Таблица 1. Точность аппроксимации численного решения уравнения (4.3) (



Длина шага интегрирования,
ЧИСЛЕННОЕ РЕШЕНИЕ СТОХАСТИЧЕСКОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ МЕТОДОМ ЭЙЛЕРА-МАРУЯМЫ
Кузнецова И.Ю.
Аспирант, Южный федеральный университет
ЧИСЛЕННОЕ РЕШЕНИЕ СТОХАСТИЧЕСКОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ МЕТОДОМ ЭЙЛЕРА-МАРУЯМЫ
Анностация
В данной статье описан один из наиболее популярных численных методов решения стохастических дифференциальных уравнений. В статье даны определение основной концепции, описание простейшего численного метода, а также понятие сходимости решений стохастических дифференциальных уравнений. Решениями являются непрерывные вероятностные процессы, что может быть использовано при прогнозировании процесса потребления энергоресурсов.
Ключевые слова: стохастические дифференциальные уравнения, численные методы, сходимость, порядок аппроксимации.
Kuznetsova I.Y.
Postgraduate student, Southern Federal University.
NUMERICAL SOLUTION OF STOCHASTIC DIFFERENTIAL EQUATION BY EULER-MARUYAMA METHOD
Abstract
In the article described one of the most popular numerical methods for solving stochastic differential equations. It includes a review of fundamental concepts, a description of elementary numerical methods and the concepts of convergence and order for stochastic differential equation solvers. The solutions will be continuous stochastic processes that can be used for prediction process of energy consumption.
Keywords: stochastic differential equations; numerical methods; convergence; order for solvers.
СДУ стали стандартными моделями финансовых величин, таких как цены активов, процентная ставка, и их деривативов. В отличие от детерминированных моделей, таких как обыкновенные дифференциальные уравнения, которые имеют единственное решение для каждого соответствующего начального условия, СДУ имеют решения, являющиеся стохастическими процессами с непрерывным временем. Методы численного решения СДУ основаны схожей технике решения обыкновенных дифференциальных уравнений, но обобщены для обеспечения стохастической динамики.
Простейшим эффективным численным методом аппроксимации обыкновенных дифференциальных уравнений является метод Эйлера. Метод Эйлера-Маруяма является аналогом метода Эйлера для обыкновенных дифференциальных уравнений.
Рассмотрим стохастическое дифференциальное уравнение, описывающее динамику потребления электроэнергии в ВУЗе [2,3]:

с начальным условием

где 



Зафиксируем равномерную сетку
где T — длина рассматриваемого временного промежутка, n — количество месяцев в рассматриваемом промежутке времени, Δt — шаг по времени.
Также введем следующие обозначения:
Проинтегрируем исходное уравнение (1) на промежутке 

Переходя к конечным разностям из (3) и определения стохастического интеграла, имеем,

где 

то есть ξi — случайная величина, распределенная по нормальному закону с нулевым математическим ожиданием и единичной дисперсией.
Найдем порядок сходимости метода Эйлера-Маруямы для (1).
Говорят, что численное решение 


В дальнейшем мы будем определять скорость сильной сходимости приближенного решения через понятие порядка. Решение СДУ сходится сильно с порядком m, если математическое ожидание ошибки имеет m-ый порядок от шага, то есть для любого момента времени T,
для достаточно малого размера шага 
Воспользуемся разложением Тейлора-Ито на 

Вычислив повторные интегралы, разложение (6) можно записать в виде:
Откуда получим, что

где 


Хотя метод Эйлера для обыкновенных дифференциальных уравнений имеет первый порядок, метод Эйлера-Маруямы для стохастических дифференциальных уравнений имеет порядок 0,5. Этот факт доказан Гикхманом и Скороходовым в 1972 году.
На основании данных по потреблению электроэнергии за 2010-2011гг. общежитиями студенческого городка ЮФУ в г. Таганроге и предложенной модели (1) были получены следующие прогнозные значения потребления электроэнергии на 2012 год, которые были сравнены с данными по потреблению электроэнергии за тот же период.
При применении метода Эйлера-Маруямы (4) к модельному уравнению (1) были получены следующие результаты:
Рис. 1 – График потребления электроэнергии на 2012 г.
——— — прогнозные данные на 2012 г. по потреблению электроэнергии,
полученные с помощью метода Эйлера-Маруямы (2.27);
– – – – – – — реальные данные по потреблению электроэнергии за 2012 г.
Определение качества модели проводилось по следующим параметрам:

где 

где 
где 

- Средняя относительная ошибка прогноза:
где 

где 

где n — длительность периода прогнозирования в месяцах.
где 

Полученные результаты представленным в таблице 1.
| Метод Эйлера-Маруямы | |
| Среднеквадратичное отклонение (нормированное) | 0,167 |
| Средний процент ошибки | 10,2% |
| Средняя относительная ошибка прогноза | 18,3% |
| Коэффициент детерминации | 0,61 |
| Индекс Тейла | 0,123 |
На основании полученных результатов можно сделать вывод о применимости рассматриваемой модели (1) к прогнозированию потребления электроэнергии.
Численные методы решения стохастических дифференциальных уравнений играют важную роль при анализе случайных процессов. Несмотря на то, что скорость сходимости к сильному решению для метода Эйлера-Маруямы составляет всего 0,5, его популярность в сфере финансов обусловлена тем, что он «прост» в построении разностной схемы и не требует большого объема вычислительных ресурсов. Это позволяет применять его для определения качества построенных моделей. Применение численных методов более высоких порядков ведет к резкому возрастанию необходимых вычислительных ресурсов, при этом точность прогноза может изменяться незначительно.
Литература
- Андерсон Т. – Статистический анализ временных рядов, М.: «Мир», 1980.
- Кузнецова И.Ю. Математическая модель прогнозирования энергопотребления // Известия Южного федерального университета. Технические науки. — — №4 — С. 121-125.
- Кузнецова И.Ю. Математическая модель энергопотребления применительно к ВУЗу // Известия Южного федерального университета. Технические науки. — — Т.121 №8 — С. 183-186.
- Кузнецова И.Ю.Численное решение стохастических дифференциальных уравнений в финансах // Известия Южного федерального университета. Технические науки. — — №4 — С. 175-184.
- Turner Wayne C., Doty S., Energy management handbook // Library of Congress Cataloging-in-Publication Data. — 6th ed., 2007. — 924 p.
Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
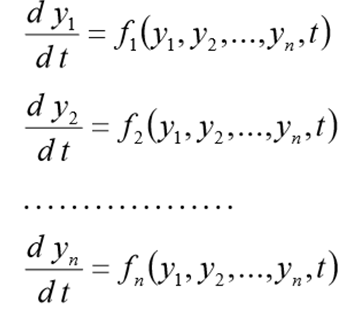
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши


по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 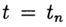

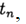


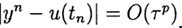


При 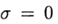
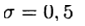
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
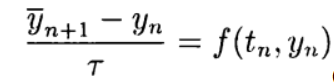
а на этапе корректора (уточнения) — схема
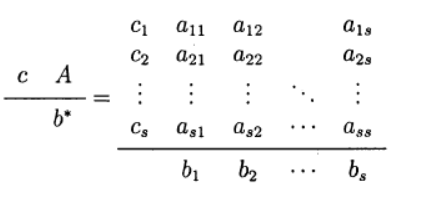
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
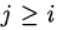

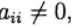
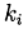
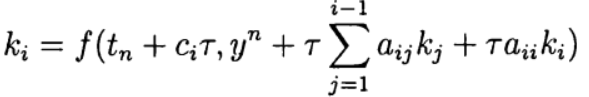
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 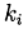
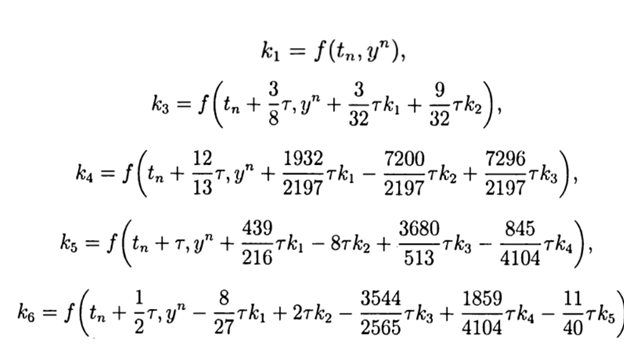
С учётом(9) общее решение имеет вид:
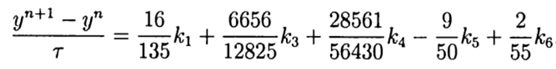
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
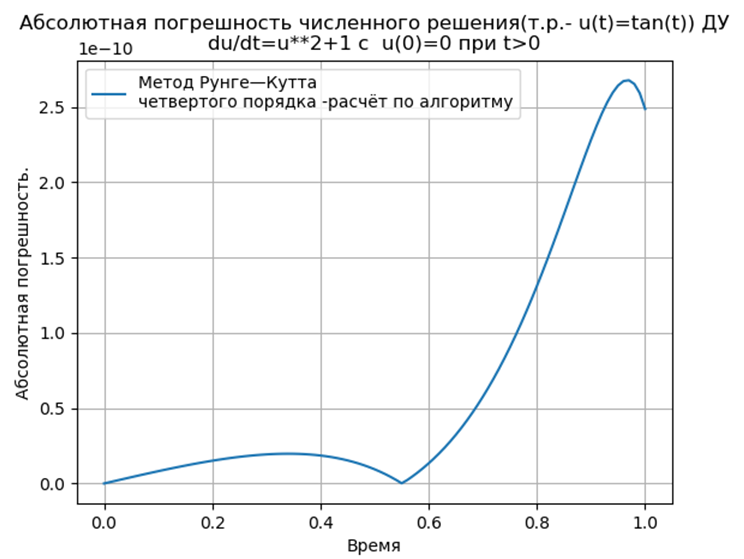
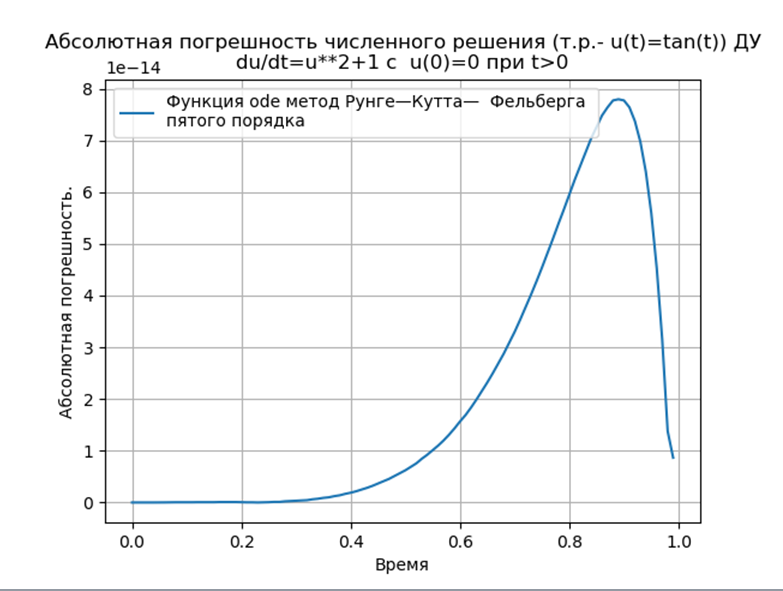
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
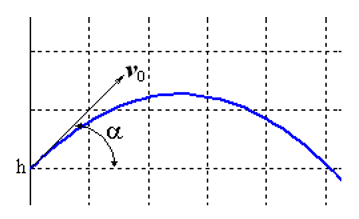
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 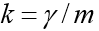
К системе следует добавить начальные условия: 

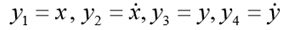
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
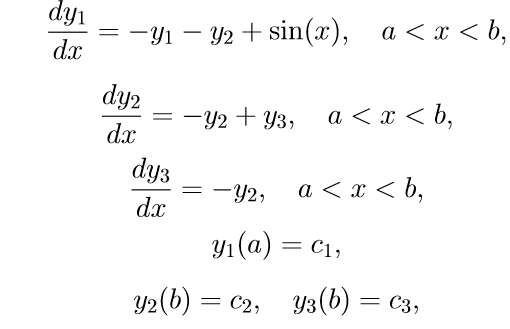
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 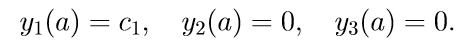
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 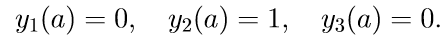
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 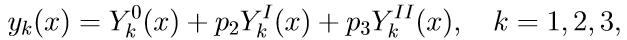
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
http://research-journal.org/physics-mathematics/chislennoe-reshenie-stoxasticheskogo-differencialnogo-uravneniya-metodom-ejlera-maruyamy/
http://habr.com/ru/post/418139/

















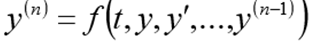
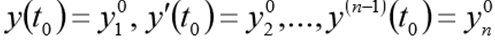


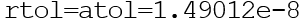
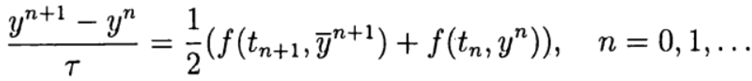
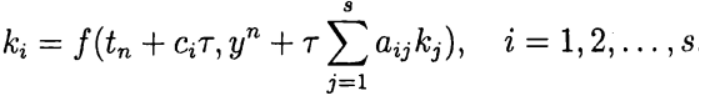
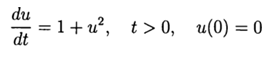 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга