Численное решение уравнения теплопроводности на с

Метод Finite Volume — реализация на примере теплопроводности

Метод Finite Volume (FVM)

В основе метода лежит разбиение области на непересекающиеся контрольные объемы(элементы), узловые точки, в которых ищется решение.Узловые точки находятся в центрах контрольных объемов.Также, как и для метода конечных разностей, для каждого элемента составляется уравнение, получается система линейных уравнений.Решая ее — находим значения
искомых переменных в узловых точках.Для отдельного элемента уравнение получается путем интегрирования исходного дифф уравнения по элементу и аппроксимации интегралов.

Термин конечный объем в статье будет часто заменятся на Элемент, будем для удобства считать их эквивалентами (элемент в данной статье не имеет ничего общего с методом конечных элементов).

Есть 2 различных способа решения задачи по FVM:
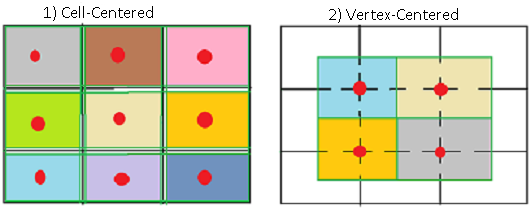
1) грани контрольного объема совпадают с гранями элемента
2) грани контрольного объема проходят через центры граней элементов(на которые разбита область).Искомые переменные хранятся в вершинах этих элементов.Вокруг каждой вершины строится контрольный объем. Для непрямоугольной сетки этот способ имеет еще 2 подвида.

Мы будем использовать способ 1) с контрольными объемами совпадающими с элементами на которые разбита область.

Некоторые плюсы FVM:

• сохранение основных величин по всей области, таких как энергия системы, масса, тепловые потоки и тд.Причом это условие выполняется даже для грубой расчетной сетки
• высокая скорость расчета.Многие расчетные величины можно вычислить при разбиении области на элементы, и вычислять их на каждом шаге по времени нет необходимости.
• легкость использования для задач со сложной геометрией и криволинейными границами.Легкость использования разных геометрических типов элементов — треугольники, полигоны.

Метод FVM реализуем на примере уравнения теплопроводности:

Итак основные шаги при реализации FVM:

1. Перевод дифф уравнения в форму пригодную для FVM — интегрирование по контрольному объему
2. Составление дискретного аналога, выбор способа перевода производных и других подынтегральных выражений в дискретную форму
3. Получение уравнения для каждого из контрольных объемов, на которые разбита область.Составление системы линейных уравнений и ее решение.

Дискретизация по времени.

Немного теории или первый шаг в реализации FVM

FVM на стандартной прямоугольной сетке

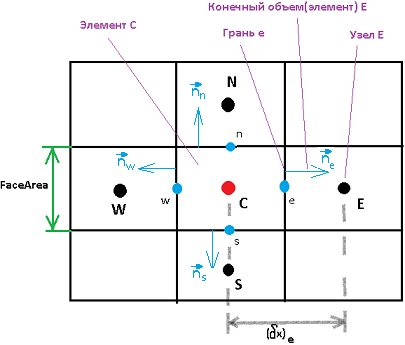
На рисунке изображен Элемент С и его соседние элементы справа(E), слева(W), сверху(N) и снизу(S).У элемента С есть 4 грани обозначенные буквами e w n s.Именно эти 4 грани и составляют периметр элемента и по ним производится интегрирование.Для каждого элемента в результате получаем дискретный аналог исходного дифф уравнения.

Составим дискретный аналог для элемента С.Для начала нужно разобраться с интегралом (3).Интеграл это ведь по факту сумма.Поэтому мы и заменяем интеграл по всей поверхности элемента, на сумму по 4-м составляющим этой поверхности, тоесть 4 граням элемента.

Уравнение (7) и есть конечное уравнение для элемента С, из него мы на каждом шаге по времени получаем новое значение температуры (Tnew) в элементе С.

Граничные условия на прямоугольной сетке

Мы рассмотрим только 2 вида граничных условий.

1. Задана температура Tb на границе
2. Задан поток FluxB на границе, рассмотрим только случай когда FluxB=0, т.е. грань e будет теплоизолирована(Insulated)

Случай 2) самый простой, поскольку получается что грань e не потребуется при дискретизации(т.к. все коэффициенты Flux=0) и можно ее просто пропустить.

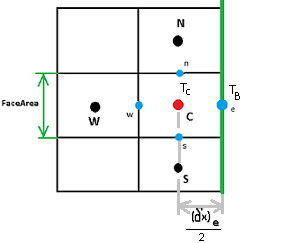
Теперь рассмотрим случай 1).Дискретизация грани e будет в целом похожа на ту что уже была описана.Будут только 2 изменения — вместо Te будет известное граничное значение Tb и вместо расстояния DXe будет DXe/2.В остальном можно рассматривать значение Te так, как будто это был бы обычный соседний узел E.Теперь подробнее распишем терм для граничного элемента С.

Пример численных расчетов на прямоугольной сетке

FVM в задачах со сложной геометрией

Здесь как раз проявляется преимущество FVM, где также, как и в методе конечных элементов, можно представлять область с круглыми границами через разбиение на треугольники или любые другие полигоны.Но FVM имеет еще 1 плюс — при переходе от треугольников к полигонам с большим числом сторон не требуется абсолютно ничего менять, конечно если код был написан для произвольного треугольника а не равностороннего.Более того, можно без изменения кода использовать смесь разных элементов — треугольники, полигоны, квадраты и тд.

Рассмотрим общий случай, когда вектор соединяющий центры 2-х элементов не совпадает с вектором нормали к общей грани этих элементов.Вычисление потока flux через грань теперь будет состоять из 2-х частей.В первой будет расcчитываться ортогональная составляющая а во второй так называемая «кросс-диффузия».

На картинке изображены 2 элемента, С — текущий рассматриваемый элемент и F — соседний элемент.Опишем дискретизацию для грани, разделяющей эти 2 элемента.Вектор соединяющий центры элементов — DCF.Вектор e — это единичный вектор по направлению DCF.Вектор Sf — направлен по нормали к грани, его длинна равна длине грани.

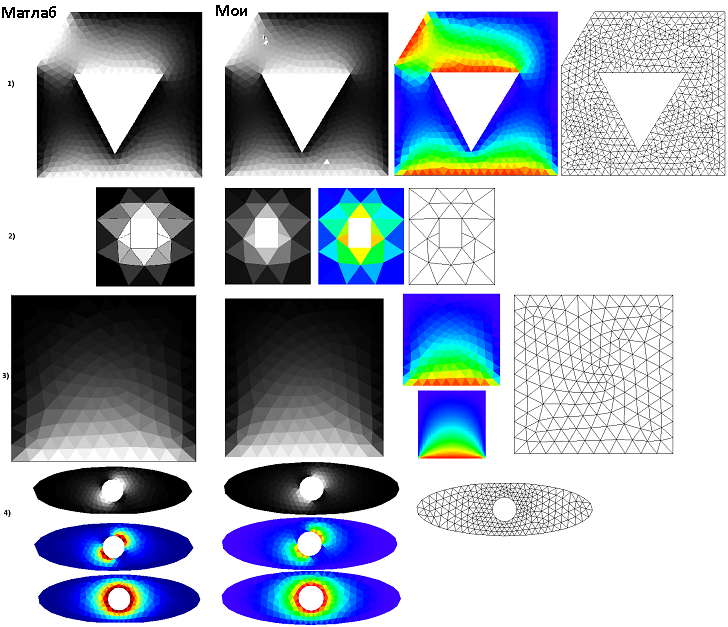
В исходниках я не стал реализовывать терм с кроссдиффузией, т.к встал вопрос — как проверить корректность такой реализации.Визуально сравнение результатов Матлаб и моих ничем не отличалось в отсутствии кросс-диффузии.Видимо это связано с тем что Матлаб любит треугольники близкие к равносторонним, что в итоге делает кроссдиффузию=0.Возможно позже еще вернусь к этому вопросу.

Расчет граничных элементов ничем не отличается от расчетов не на границе, вместо центра соседнего элемента берется центр грани, ну и как обычно подставляется температура на границе.
В моей реализации в итоге получается так:

Примеры и проверка результатов

Описание структуры исходников

Гитхаб с исходниками лежит тут
Основная версия в папке heat2PolyV2.То что относится к вычислительной части лежит в heat2PolyV2\Src\FiniteVolume\.

Вначале файла Scene2.cs — параметры которые можно менять для отображения в разных цветовых схемах, масштаб, отображение mesh и т.д.Сами примеры хранятся в heat2PolyV2\bin\Debug\Demos\
Выгрузку из Матлаба сделать просто — нужно открыть pde toolbox, открыть m файл (либо создать самому с нуля), зайти в меню Mesh-Экспорт mesh, нажать ОК; перейти в основной Матлаб, в панельке появятся переменные — матрицы p e t, открыть файл savemymesh.m, выполнить его, появится файл p.out, перенести его в папку Demos.
В исходниках для выбора примера необходимо задать имя файла в строке param.file = «p»;(FormParam.cs).Далее необходимо применить граничные условия — для готовых примеров можно просто раскомментировать соответствующие блоки в MainSolver.cs:

Смысл тут простой — Матлаб разделяет границы по доменам, например внешние и внутренние.Также для каждого домена границы разбиты на части (группы), чтобы можно было задавать условия на участках границы по отдельности — например справа или снизу.
Возможно и вовсе не использовать Матлаб, а вручную прописать все элементы(треугольники) и их вершины + грани(только для граничных элементов)

Аналитический и численный методы решения уравнения теплопроводности Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Карпович Дмитрий Семенович, Суша Оксана Николаевна, Коровкина Наталья Павловна, Кобринец Виктор Павлович

В данной статье приводится сравнение методов решения уравнения теплопроводности. Подробно рассмотрено решение аналитическим методом. Заданы условия однозначности, а также начальные и граничные условия и приведены способы их задания с учетом физических особенностей моделирования теплопроводности режущего инструмента. Составлено и решено уравнение методом разделения переменных , в виде произведения двух функций, и разложено в ряд Фурье с заданными параметрами, определяемыми характеристическим уравнением. Получено окончательное выражение распределения температуры в инструменте. Также приведен пример решения численным методом тепловых балансов, выведено уравнение в конечно-разностной форме для расчета распределения температурного поля и получено приближенное решение для температур в узловых точках. Проанализированы характерные особенности каждого метода решения одномерной нестационарной задачи теплопроводности. Представлены графики распределения температуры в инструменте для интервала времени с разным количеством элементов ряда. Сделан вывод о точности и вычислительной сложности при решении каждой рассмотренной задачи. В заключение раскрываются достоинства и недостатки аналитического и численного методов и приводится обоснование использования модифицированного численного метода в одномерной нестационарной задаче теплопроводности.

Похожие темы научных работ по математике , автор научной работы — Карпович Дмитрий Семенович, Суша Оксана Николаевна, Коровкина Наталья Павловна, Кобринец Виктор Павлович

Текст научной работы на тему «Аналитический и численный методы решения уравнения теплопроводности»

ИНФОРМАТИКА И ТЕХНИЧЕСКИЕ НАУКИ

МОДЕЛИРОВАНИЕ ПРОЦЕССОВ И УПРАВЛЕНИЕ В ТЕХНИЧЕСКИХ СИСТЕМАХ

Д. С. Карпович, О. Н. Суша, Н. П. Коровкина, В. П. Кобринец

Белорусский государственный технологический университет

АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

В данной статье приводится сравнение методов решения уравнения теплопроводности. Подробно рассмотрено решение аналитическим методом. Заданы условия однозначности, а также начальные и граничные условия и приведены способы их задания с учетом физических особенностей моделирования теплопроводности режущего инструмента. Составлено и решено уравнение методом разделения переменных, в виде произведения двух функций, и разложено в ряд Фурье с заданными параметрами, определяемыми характеристическим уравнением. Получено окончательное выражение распределения температуры в инструменте. Также приведен пример решения численным методом тепловых балансов, выведено уравнение в конечно-разностной форме для расчета распределения температурного поля и получено приближенное решение для температур в узловых точках. Проанализированы характерные особенности каждого метода решения одномерной нестационарной задачи теплопроводности. Представлены графики распределения температуры в инструменте для интервала времени с разным количеством элементов ряда. Сделан вывод о точности и вычислительной сложности при решении каждой рассмотренной задачи.

В заключение раскрываются достоинства и недостатки аналитического и численного методов и приводится обоснование использования модифицированного численного метода в одномерной нестационарной задаче теплопроводности.

Ключевые слова: метод разделения переменных, дифференциальное уравнение, метод конечных разностей, закон Фурье, температурное поле, граничные условия.

D. S. Karpovich, O. N. Susha, N. P. Korovkina, V. P. Kobrinets

Belarusian State Technological University

THE ANALYTICAL AND NUMERICAL METHODS

OF SOLVING THE THERMAL CONDUCTIVITY EQUATION

In this article we present a comparison of the methods of solving the thermal conductivity equation. An analytical method of solving is considered in details. The conditions of unambiguity are specified, as well as the initial and boundary conditions and ways of their definition in consideration with physical features of modelling the thermal conductivity of the cutting tool. The equation is constituted and solved by the method of division of variables, as the product of two functions, and it is separated in Fourier series with the specified parameters defined by the characteristic equation. The final expression of temperature division in the tool is obtained as well. The example of solving by a numerical method of thermal balances is given too, the equation is deduced into finite-difference form to calculate

the distribution of the temperature field and the approximate solution for temperatures in central points is obtained as well. There are analyzed characteristic features of each method of solving of one-dimensional non-stationary problem of thermal conductivity. Diagrams of the temperature distibution in the tool are presented for a time interval with a different quantity of elements of series row. We made a conclusion on accuracy and computing complexity while solving each considered problem.

In conclusion we revealed the advantages and disadvantages of analytical and numerical methods and we give proof of using the modified numerical method in solving one-dimensional non-stationary problem of thermal conductivity.

Key words: the method of division of variables, the differential equation, the method of ultimate differences, Fourier’ law, a temperature field, boundary conditions.

Введение. Существует несколько методов решения задач теплопроводности: аналитический, аналоговый, численный, графический и экспериментальный. Четыре из них исходят непосредственно из различных форм уравнений. Экспериментальным методом пользуются, когда остальные методы не дают результатов. Его применяют для определения теплофизических свойств, таких как теплопроводность и удельная теплоемкость.

Для решения задач теплопроводности в твердых телах сложной формы используются аналитические и численные методы. Решения возможны при известных краевых условиях, включающих начальное распределение температур в теле и граничные условия на поверхности тела, которые могут быть заданы одним из трех способов: температурой поверхности, тепловым потоком и коэффициентом теплоотдачи [1].

Аналитическое решение задач нестационарной теплопроводности методом разделения переменных Фурье предпочтительнее других методов при неравномерном начальном распределении температуры в теле и в тех случаях, когда нет необходимости в расчетах для очень малых времен от начала процесса.

Из численных методов решения задач теплопроводности в настоящее время наиболее ценным и широко используемым является метод конечных разностей.

Основная часть. Дифференциальное уравнение теплопроводности при отсутствии внутренних источников теплоты имеет вид

Данное уравнение известно как закон (или постулат) Фурье.

Условия однозначности задаются в виде: физических параметров X, с, р; формы и геометрических размеров объекта 10, А, /2, . 4; температуры тела в начальный момент времени т = 0:

Граничные условия могут быть заданы в следующем виде:

t (Х = Хнач ) = ^ t (Х = Хкон ) = t2 *

Решить задачу теплопроводности — значит установить зависимость между температурой t, временем т и координатами тела x, y, z.

Рассмотрим режущий инструмент толщиной 25. Если толщина инструмента мала по сравнению с длиной и шириной, то такую полоску обычно считают неограниченной.

При заданных граничных условиях коэффициент теплоотдачи а одинаков для всех точек поверхности инструмента. Изменение температуры происходит только в одном направлении x, в двух других направлениях температура не изменяется, следовательно, в пространстве задача является одномерной. Начальное распределение температуры задано некоторой функцией t(x, 0) = fx). Охлаждение происходит в среде с постоянной температурой tw = const. Отсчет температуры инструмента для любого момента времени будем вести от температуры окружающей среды. Поскольку задача в пространстве одномерная, то дифференциальное уравнение (1) принимает вид

Начальные условия: при т = 0

3 = -Эо = / (х) -*ж = Р (х). (3)

Решение дифференциального уравнения (2) ищем в виде произведения двух функций, из которых одна является функцией только т, а другая — только х (метод разделения переменных):

После подстановки последнего выражения в дифференциальное уравнение (2) имеем:

Левая часть уравнения (5) есть функция только т, а правая — функция только х.

Решая уравнение (5), находим частное решение:

Подчинив частное решение граничному условию, после простейших преобразований получим значения корней характеристического уравнения:

31 = Л1 С08| ц — I е

32 = Л.2С08|Ц28|е 2 82 ;

3п = Л Н Цп 8| е ^82

Полученные частные решения будут удовлетворять дифференциальному уравнению при любых значениях постоянных, но ни одно из этих решений не будет соответствовать действительному распределению температуры в начальный момент времени [3]. Однако путем наложения бесконечного числа таких распределений при соответствующем выборе величин Ап можно воспроизвести любую действительную температурную зависимость в начальный момент времени.

На основании сказанного общее решение можно представить суммой бесконечного ряда:

ч 2 ат X Ч ЦП «Г

Известно, что если отдельные распределения (7) удовлетворяют дифференциальному уравнению (2) и граничным условиям, то и сумма их также удовлетворяет тем же условиям. Постоянная Ап в уравнении найдется из начальных условий.

Окончательное выражение для случая равномерного распределения температуры в инструменте в начальный момент времени:

| Цп7 |е 81И Цп С08 Цп I 8

Следует отметить, что если получение точного аналитического решения связано с трудностью удовлетворения граничных условий, которые не всегда осуществимы, то при помощи численного метода всегда возможно, по крайней мере приближенно, удовлетворить граничным условиям конкретной задачи.

Получим расчетную формулу для численного интегрирования одномерной нестацио-

нарной задачи методом тепловых балансов. Пусть в этом случае процесс теплопроводности описывается уравнением

Рассмотрим применение метода к расчету температурного поля в режущем инструменте (уравнение (10)).

Разбиваем на элементарные объемы. Полагаем, что удельная теплоемкость с и коэффициент теплопроводности X в пределах элементарного участка постоянны. Очевидно, количество теплоты, подводимое стержнем к узловой точке, определится по закону Фурье. Если расстояние 5 достаточно мало, то можно выразить q через конечные:

Изменение внутренней энергии в рассматриваемой узловой точке за время Дт:

и = ерУА!’ = ерУ(!’ — t),

где с — удельная теплоемкость; р — плотность вещества; У — элементарный объем; ! — температура в данной узловой точке в момент времени т; !’ — температура в момент времени т + Дт.

С учетом сказанного уравнение теплового баланса для узловой точки будет иметь вид

Решая последнее уравнение относительно неизвестной температуры получаем:

Если учесть, что X / ср = а — коэффициент температуропроводности вещества, У = 52 и Дта / 82 = F0 — число Фурье, то уравнение (13) принимает вид

Уравнение (14) является основой численного метода расчета нестационарной теплопроводности.

Используем полученные формулы для преобразования дифференциального уравнения к конечно-разностной форме. Преобразование проведем на примере одномерной нестацио-

нарной задачи теплопроводности безграничной стенки (уравнение (10)).

Поскольку температура ¿(х, т) является функцией двух переменных, удобно выбрать прямоугольную сетку. Весь интервал изменения х от 0 до 1 по оси абсцисс разобьем на одинаковые интервалы 5х, а отрезок времени от т = 0 до т = & разделим на равномерные интервалы 5т (рис. 1).

х = 5х х = 25х х = т5х х = I х

Рис. 1. Сетка для составления уравнений

Восстановленные перпендикуляры к координатным осям в точках деления при пересечении образуют расчетные узловые точки. Тогда температура для узловой точки 1 с координатами х = тЪх и т = к5т запишется так:

Для точки 2 с координатами х = тЪх и т + 5т = (к + 1)5т имеем:

¿2 = ¿2(т5 х (к + 1)5Т) = 1п

для точки 3 с координатами х + 5х = (т + 1)5х и т + 5т = (к + 1)5т получим:

¿3 = ¿з[( т +1) 5 х,(к +1) 5Т) = г,

Заменим в точке 1 (т5х, £5т) частные производные в уравнении теплопроводности разностными отношениями:

= ТТ(^+1,к — 2(т,к + ¿т-1,к ) + 8 2, (16)

В этих выражениях е1 и е2 — остаточные члены, учитывающие переход от производных функций к разностным отношениям. Можно показать, что эти члены стремятся к нулю при стремлении к нулю интегралов разбиения 5х и 5т. Дифференциальное уравнение в конечно-разностной форме запишется следующим образом:

Решая уравнение (17) относительно будущей температуры ¿тк+1 в рассматриваемой точке, получим:

Очевидно, остаточный член в уравнении (18) будет стремиться к нулю при стремлении к нулю 5т. Следовательно, чем более мелкие интервалы выбраны для сетки узловых точек, тем меньше ошибка перехода от дифференциального уравнения к уравнению в конечных разностях. Ошибки в1 и е2 можно оценить, воспользовавшись разложением функции t в ряд Тейлора.

Отбрасывая остаточный член в уравнении (18) и обозначая приближенное значение величины ¿тк через Ттк, получим приближенное решение для будущей температуры в узловой точке (т5х, к5т):

Проанализируем формулы (9) и (19). И одна, и вторая формулы являются окончательными формулами для расчетов распределения теплового поля [3]. В данной программе мы производим вычисление температуры в ста точках инструмента для пятидесяти моментов времени. Для каждой из этих точек нахождение температуры требует вычисления суммы нескольких элементов. На рис. 2 показано поле распределения температуры при количестве элементов ряда п = 10.

1401 120 -10080 -6040 20 60

Рис. 2. Поле распределения температур при п = 10

Как видно из графика, при таком значении п решение по оси х имеет колебательные свойства. Это объясняется тем, что в формуле (9) присутствует тригонометрические функции синуса и косинуса.

При увеличении числа п данные колебательные свойства будут проявляться слабее. Действительно, на рис. 3 можно наблюдать то же поле распределения температур, но при величине п = 100.

103! 102 101! 100 99 98

Рис. 3. Поле распределения температур при п = 100

Сравнивая эти графики, можно прийти к выводу о том, что для получения распределения температуры в инструменте приемлемой точности необходимо выбирать достаточно большие значения п. Однако при этом вычислительная сложность задачи многократно возрастает. Для случая п = 100 компьютеру необходимо провести расчет 50^100^100 раз. Вычисление формулы (9) в количестве 500 000 раз является весьма длительным процессом даже на современных специализированных быстродействующих ЭВМ. Это объясняется также тем, что, кроме большого числа вычислений формулы, необходимо каждый раз рассчитывать значения синусов и косинусов. Для вычисления синуса или косинуса ЭВМ раскладывает

его в достаточно большой ряд, что еще более усиливает сложность расчетов.

В случае же реализации формулы (19) для такого же количества точек по осям времени t и длины х вычислительная сложность задачи значительно уменьшается (рис. 4).

Рис. 4. График решения уравнения теплопроводности численным методом

Действительно, для нахождения значения температур в ста точках инструмента при пятидесяти различных моментах времени необходимо будет вычислить 5000 раз формулу (19), что в сто раз меньше по сравнению с расчетом формулы (9). Кроме того, при вычислении формулы (19) отсутствует необходимость рассчитывать значения синусов и косинусов или любых других сложных математических функций.

Заключение. Проанализировав аналитическое решение уравнения теплопроводности, можно сделать вывод, что решение удается получить только для простейших условий, для тел простой формы, при этом отмечается высокая вычислительная сложность. При помощи численного метода всегда возможно удовлетворить граничным условиям задачи и решать сложные задачи, недоступные для аналитических методов. Вычислительная сложность задачи значительно меньше.

1. Суша О. Н., Карпович Д. С. Моделирование температурного поля в дереворежущем инструменте с использованием программы ANSYS // Энерго- и ресурсосберегающие технологии и оборудование, экологически безопасные технологии. Минск, 2014. С. 44-48.

2. Кудинов В. А., Кудинов И. В. Методы решения уравнений теплопроводности. Самара, 2012. 280 с.

3. Карпович Д. С. Моделирование и численное решение уравнения теплопроводности // Энерго-и ресурсосберегающие технологии и оборудование, экологически безопасные технологии. Минск, 2014. С. 311-313.

1. Susha O. N., Karpovich D. S. Simulation of temperature field in the wood-cutting tools with the ANSYS. Energo- i resursosberegayushchiye tekhnologii i oborudovanie, ekologicheski bezopasnyye

tekhnologii [Energy-saving technologies and equipment, environmentally friendly technologies], Minsk, 2014, pp. 44-48 (In Russian).

2. Kudinov V. A., Kudinov I. V. Metody reshenija uravnenij teploprovodnosti [Methods for solving the heat equation], Samara, 2012. 280 p.

3. Karpovich D. S. Modeling and numerical solution of the heat equation. Energo- i resurso-sberegayushchiye tekhnologii i oborudovanie, ekologicheski bezopasnyye tekhnologii [Energy-saving technologies and equipment, environmentally friendly technologies], Minsk, 2014, pp. 311-313 (In Russian).

Методы решения УЧП

МЕТОДЫ РЕШЕНИЯ УЧП

1. Уравнение теплопроводности

Рассмотрим численное решение уравнений с частными производными (УЧП) на примере решения уравнения теплопроводности (диффузии)

— плотность тепловых источников, — коэффициент теплопроводности

Если , то мы имеем стационарное уравнение теплопроводности

— уравнение Пуассона.

Если плотность тепловых источников тоже равна 0, то получаемое уравнение называется уравнением Лапласа.

Стационарное уравнение теплопроводности может быть решено, если известны граничные условия.

Это могут быть или значения искомой функции на границе (задача Дирихле).

Или значения потока тепла на границе (задача Неймана)

Либо смешанные условия.

Если необходимо решать УЧП в области, имеющей круговую симметрию, оператор Лапласа удобна записать в полярных координатах:

2. РЕШЕНИЕ СТАЦИОНАРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

Будем решать задачу Дирихле для уравнения Пуассона.

в прямоугольной области , .

Для численного решения данной задачи применим метод SOR (метод последовательной верхней релаксации). Вначале используем метод конечных разностей. Для этого разобьем отрезок [a, b] на K равных интервалов длиной , а отрезок [c, d] — на L интервалов той же длины. Пусть при этом , . Тогда

Таким образом, мы разбили весь прямоугольник , на квадраты со стороной ,получив при этом сетку (решетку). Будем искать нужную нам функцию в узлах этой решетки методом конечных разностей. То есть будем искать эту функцию в виде матрицы

Запишем вначале в одномерном случае рамках метода конечных разностей производную функции U по х в точке . Получим

Для второй производной в точке получим

Аналогичным образом, для второй производной в точке имеем

Перейдем теперь к двумерной области и найдем вторые производные в точке , .

,

Подставив полученные таким образом вторые производные в уравнение Пуассона, имеем

Коэффициенты перед матричными элементами в данном случае равны 1 и 4. Однако в общем случае (полярные координаты, например) мы должны записать

и вычислить A, B, C, D, E.

Перепишем полученное нами уравнение в следующем виде:

Разность между левой и правой частями уравнения называется невязкой

Подставляя в правую часть (3) уравнение (1) имеем

Уравнение (4) является тождеством. Его можно использовать в случае, когда решение ищется методом последовательных приближений

Это и есть основное уравнение метода SOR. Параметр обычно выбирается не тождественно равным 1, изменяющимся параметром от 1 до 1.5. Это делается для лучшей сходимости метода. В качестве начального приближения берется функция, тождественно равная 0 внутри области определения и равная граничным условиям на границе области.

3. РЕШЕНИЕ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

Будем искать решение этой задачи методом Кранка-Николсона. Рассмотрим вначале одномерное нестационарное уравнение диффузии.

Запишем производную по времени в k-й точке х в n-й момент времени в виде:

Здесь — шаг по времени. В правой части вторую производную по координате можно взять как в момент времени ,

так и в момент времени

Суть метода Кранка-Николсона заключается в том, что производная в правой части берется как среднее арифметическое от производных в точках и . То есть

Для двумерного уравнения диффузии

в рамках метода Кранка-Николсона запишем вторые производные по х и по у

как среднее арифметическое от производных в точках и ,

перенесем все значения функции в момент времени влево, а в — й вправо. Получим.

,

(1)

(2)

Схема расчета по методу Кранка-Николсона такова:

1. В начальный момент времени из начальных и граничных условий методом SOR (или каким-либо другим методом) находим значения функции U.

2. Вычисляем с ее помощью в этот же момент времени по формуле (2) функцию F.

3. По формуле (1) с помощью уже вычисленной функции F и граничных условий находим значение функции U в следующий момент времени.

4. Вычисляем с ее помощью по формуле (2) функцию F.

5. По формуле (1) находим значение функции U в следующий момент времени.

МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

4. Решение одномерного уравнения теплопроводности

Базисные функции метода конечных элементов

Суть метода в том, что искомая функция ищется интерполяцией с помощью базисных функций. В этом случае отпадает необходимость расчета производных методом конечных разностей.

Пусть отрезок [a, b], на котором определяется искомая функция, разбит N точками на (N-1) равных отрезков (конечных элементов) длиной . На рисунке показан случай, когда N = 4.

Значения функции в этих точках равны , , . , . на каждом из конечных элементов функцию u(x) можно представить с помощью базисных функций :